[solafune] 夜間光データから土地価格を予測ベースモデル

はじめに

衛星データに特化したデータ分析コンペサイトsolafuneにて、主題のコンペが2021/2/15~2021/4/5の間で開催されています。

衛星データのコンペと言っても画像データを扱うわけではなく、衛星によって取得された夜間光のデータ+地域ごとの地価データを1ファイル1MB以下のcsvファイルにしたデータを扱うもので、初心者にも非常に参加しやすいコンペとなっています。列数でいえばあのデータ分析の登竜門Titanic以下の4列（予測対象の1列除く）しかありませんし、国内コンペでは珍しく5位入賞まで賞金が出るおまけつきです。

この記事ではそんなコンペ開催を記念して、そして最もコンペに貢献したコンテンツを書いた人に贈られれるSolafune賞を狙って以下の様な方を対象にベースラインモデルを紹介します。

• Titanicはやったのでデータ分析コンペに参加してみたい！
• Kaggleスタートブック本以上Kaggle本未満程度の知識がある。
  • 記事中では例えば以下の様な言葉は説明なしに登場し、触れたとしてもごく少量の説明で各種ライブラリの使用等を行います。また、ipynbファイルでの作業を想定しており、ライブラリのインストール等を含めた環境構築も完了していることを前提としています。
  • 訓練（train）データ、評価（test）データ
  • EDA
  • 特徴量エンジニアリング
  • 交差検証
  • LightGBM
  • 評価指標
  • などなど...

この記事よりもハイレベルな（そしてスコアが高い）ベースラインも別の参加者の方が投稿されていますので、そちらも是非ご確認ください！

ベースラインモデル

まずは何はともあれSolafuneへの登録、コンペへの参加登録、配布データのダウンロードを行っておいてください。ディレクトリ構成は以下を想定しています。

├── data
│   ├── TrainDataSet.csv       <- 配布データ1
│   ├── EvaluationData.csv     <- 配布データ2
│   └── UploadFileTemplate.csv <- 配布データ3
│
└── notebook                    <- .ipynbファイルの保存場所

基本ライブラリのインポート＆データ読み込み

import os
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_theme(style="ticks")

# データを保存しているフォルダのディレクトリ指定
DATA_DIR = '../data/'

# データ読み込み
train = pd.read_csv(os.path.join(DATA_DIR, 'TrainDataSet.csv'))
test = pd.read_csv(os.path.join(DATA_DIR, 'EvaluationData.csv'))
submission = pd.read_csv(os.path.join(DATA_DIR, 'UploadFileTemplate.csv'))

1つ、補足します。EvaluationData.csvをtestとして読み込んでいますが、これはデータ分析コンペサイトの中でもSolafune独特のファイル名が付けられていることによります。evaluationと名付けられていますがこれが他で言うtestデータのことであり、交差検証の時に出てくるvalidationデータとは別物ですのでご注意ください。

簡単にデータのサイズや中身を見てみます。

# shapeの表示
print(f'train     : {train.shape}')
print(f'test      : {test.shape}')
print(f'submission: {submission.shape}')

train     : (21883, 5)
test      : (13860, 4)
submission: (13860, 3)

# 先頭3行の表示
print('# train')
display(train.head(3))

print('# test')
display(test.head(3))

print('# submission')
display(submission.head(3))

# train

	PlaceID	Year	AverageLandPrice	MeanLight	SumLight
0	1128	1993	740.909091	57.571430	403.0
1	1128	1994	739.390909	62.714287	439.0
2	1128	1995	739.390909	61.857143	433.0

# test

	PlaceID	Year	MeanLight	SumLight
0	1387	1992	28.775862	3338.0
1	1387	1993	36.948277	4286.0
2	1387	1994	30.706896	3562.0

# submission

	PlaceID	Year	LandPrice
0	1387	1992	0
1	1387	1993	0
2	1387	1994	0

trainにのみあるAverageLandPriceが予測対象の列です。submissionの列名はLandPriceになっていますが特に意味はなさそうです…とにかくtrainで学習し、testのAverageLandPriceを予測、submissionの形式で提出することを目指します。

各列の説明をコンペサイトから引用しておきます。

列	内容	備考
PlaceID	地域ごとのデータ	地域固有のID
Year	年代	1992~2013年まで
AverageLandPrice	土地の平均価格	1992~2013年まで
MeanLight	夜間光量の平均値	0~63までのレンジでその地域の平均光量
SumLight	夜間光量の合計値	その地域の合計光量

コンペサイトには各情報の引用元が記されており、AverageLandPriceについては以下の通り説明されています。

地価公示（国土交通省）を元に弊社が集計、加工したものを使用しています。

公式に「この記載はデータが日本国内の地域に絞られていることを意味するか」と質問したところ「回答不可」とのことでしたが、引用元に海外の各地域の地価情報を示すものは無かったため、確証はありませんが日本国内の地域のデータに絞られている可能性が高いと勝手に思っています。

MeanLightとSumLightについては引用元を辿ってもそれらしい記述が見当たらなかったのですが、同じデータを引用していると思われるこちらの論文に以下の記載があります。

まず夜間光は、先行研究と同じく DMSP-OLS データを用いる（NGDC 2016）。ラスタ形式で配布されて
いる同データは、各地域の 1km 四方のセルに対して夜間光の強さを 0（光が無い状態）から 63（最も光
が強い状態）までの整数値で分類するものである。図 1 は 2010 年におけるバングラデシュ周辺の状況を
示しており、中央に位置するバングラデシュの首都ダッカや、左下に位置するインドの都市コルカタなど
の地区で夜間光が強いことが確認できる。また、バングラデシュの 527 郡について夜間光の平均を集計し、
その対数をヒストグラムとして示したのが図 2 である。なお同図が双峰性の分布を示しているのは、夜間
光量の最大値（63）がトップ・コーディングされた値であることに由来する。

MeanLightは恐らく上記の方法で算出した地域別の値を平均したもの、SumLightは足し合わせたものと思われます。となると、SumLightをMeanLightで割った値はその地域のおおよその面積を表しそうです。※面積が分かるからと言って地域を特定し、その情報を学習に使うのはコンペの規約違反（未承認外部データの利用）にあたりますのでご注意ください。

EDA

もう少し詳しくデータを見ていきましょう。Kaggleスタートブック本に則ってpandas-profilingやよく比較対象にあがるsweetvizを使用しても良いのですが、せっかくなので自力で見ていきます。

まずは基本のデータ型と欠損の確認から。

train.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 21883 entries, 0 to 21882
Data columns (total 5 columns):
 #   Column            Non-Null Count  Dtype  
---  ------            --------------  -----  
 0   PlaceID           21883 non-null  int64  
 1   Year              21883 non-null  int64  
 2   AverageLandPrice  21883 non-null  float64
 3   MeanLight         21883 non-null  float64
 4   SumLight          21883 non-null  float64
dtypes: float64(3), int64(2)
memory usage: 854.9 KB

test.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 13860 entries, 0 to 13859
Data columns (total 4 columns):
 #   Column     Non-Null Count  Dtype  
---  ------     --------------  -----  
 0   PlaceID    13860 non-null  int64  
 1   Year       13860 non-null  int64  
 2   MeanLight  13860 non-null  float64
 3   SumLight   13860 non-null  float64
dtypes: float64(2), int64(2)
memory usage: 433.2 KB

train、testともにすべての列がfloat64もしくはint64の数値型で、欠損がないことがわかりました。扱いやすいですね！

続いて、列毎に更に細かく見ていきます。

AverageLandPrice

いきなりですが今回の予測対象であるこちらです。

# 普通のヒストグラム
sns.histplot(data=train, x='AverageLandPrice', bins=100)
plt.show()

​
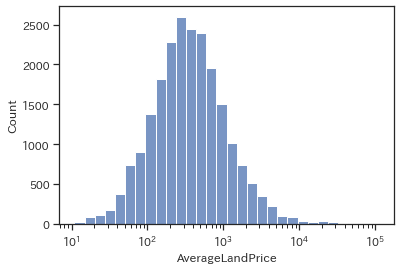
ヒストグラムを書いてみましたが0～10,000以下？がほとんどみたいですがx軸が100,000以上まであって良く分からないグラフになりました。このままでは良く分からないので対数変換して可視化してみます。

# 常用対数をとったヒストグラム
sns.histplot(data=train, x='AverageLandPrice', log_scale=10, bins=30)
plt.show()

良い感じに正規分布っぽくなりました。ほとんどが$10^3$程度以下の様ですが、数は少ないながらも大きいものだと$10^5$くらいまであるようです。※こちらの単位は公表されておらず、土地の何の平均価格かは不明です。恐らく単位千円の坪単価だとは思うのですが…確証はありません。

ベン図

残りの列は一つ一つ見ていく前に、trainとtestで共通している列なのでどのくらいデータが被っているかをベン図を書いてみます。

from matplotlib_venn import venn2

# trainとtestの共通4列の要素がどれだけ被っているかをベン図で描画
fig, axes = plt.subplots(figsize=(16, 4), ncols=4)

for c, ax in zip(test.columns, axes.ravel()):
    venn2(
        subsets=(set(train[c].unique()), set(test[c].unique())),
        set_labels=('Train', 'Test'),
        ax=ax
    )
    ax.set_title(c)

fig.tight_layout()
plt.show()

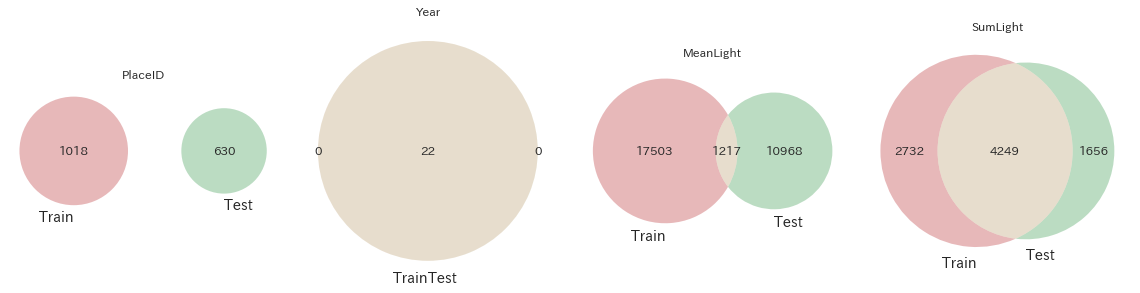
各データの数（ユニーク数）とともに、以下の様なことが分かります。

• PlaceIDはtrainとtestで全く被っていない。つまり同じ地域の情報を学習して予測するということができません。例えば東京都中央区のデータで学習して、別の地域である東京都千代田区の地価を予想するようなことが必要。（あくまで例であり、各PlaceIDが具体的にどの地域を指しているかは不明です）
• Yearはすべて共通。列名の説明で記載した通り1992~2013年の22年間分。
• MeanLightはほとんど被っていない（float64の連続値なので当たり前）
• SumLightは半分以上は被っている（float64の連続値なのに…？偶然？）

以降ベン図以外も確認していきますがAverageLandPrice以外の列はtrainとtest両方に含まれますので、一つのDataFrameに結合しておき適宜いっぺんに確認していきたいと思います。また、結合時にはどの行がtrainのデータでどの行がtestのデータかが分かる様にフラグを付けておきます。

# フラグ付け（trainには1、testには0）
train['is_train'] = 1
test['is_train'] = 0

# 結合（trainにしかない列は削除しつつ）
df = pd.concat([train.drop('AverageLandPrice', axis=1), test], ignore_index=True)

PlaceID

# is_trainフラグ毎にPlaceIDの最小値・四分位点・最大値を確認する
df.groupby('is_train')['PlaceID'].describe().iloc[:,3:]

	min	25%	50%	75%	max
is_train
0	3.0	446.0	867.0	1279.0	1662.0
1	1.0	395.5	810.0	1223.0	1660.0

train、testともに最小値・各四分位点・最大値の値がおおよそ一緒で満遍なく分割されている様です。

※PlaceIDは数値データといってもただのIDなので、最大最小や四分位数に意味がある数値ではありません。しかしながら、極端な例ですとtrainには1~1000のID、testには1001以降のIDが割り振られている様な場合は何か意味のある分割（例えばもしかするとtrainは本州でtestは本州以外で分割されているかも、など）がされている可能性があるためdescribeを使って確認しています。またもちろん、今回の様にIDがばらついていても実は意味のある分割がされていることもあります。

Year

# trainとtestで色分けしてヒストグラムの描画
sns.histplot(data=df, x='Year', hue='is_train', bins=22)
plt.show()

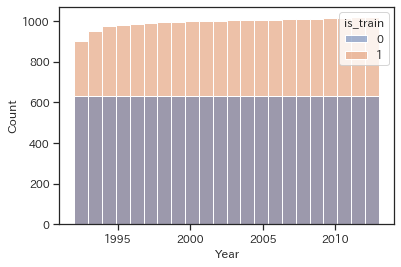
※積み上げ棒グラフの様に見えますがオレンジ(train)のヒストグラムの上に青(test)のヒストグラムが重なっています。
testはすべての年度が約600件ずつ均一にありそうですが、trainは少しだけ～1995年頃までの情報が少ない様です。

MeanLight

# trainとtestで色分けしてヒストグラムの描画
sns.histplot(data=df,x='MeanLight',hue='is_train',bins=64)
plt.show()

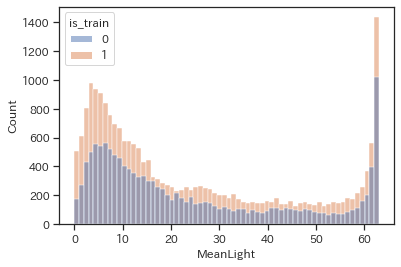
※こちらも積み上げ棒グラフの様に見えますが二つのヒストグラムが重なっています。
5近辺と最大値である63近辺に膨らみがある、双峰性の分布です。63が極端に多いのはデータの説明のところで触れた通りトップコーティングの影響と思われます。

SumLight

# trainとtestで色分けしてヒストグラムの描画
sns.histplot(data=df,x='SumLight',hue='is_train')
plt.show()

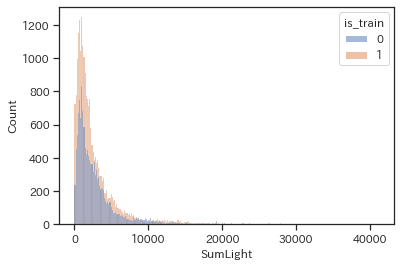
ターゲットであるAverageLandPriceと似たような形状をしており、対数変換すると正規分布に近い形になります。

AverageLandPriceと各種列

※AverageLandPriceはtestには情報がないためtrainのデータのみを使っています。

with PlaceID

sns.scatterplot(data=train, x='AverageLandPrice', y='PlaceID')
plt.show()

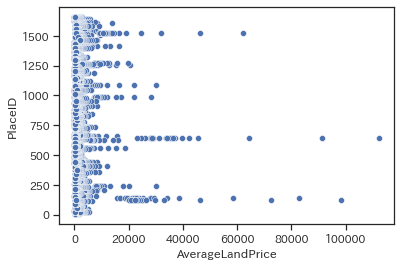
バラバラしています。やはりPlaceIDはランダムに割り振られているようです。これは例えば「同じ都道府県なら近いID」などになっていた場合、「地価が高い東京地域のIDと高い地価がもっと密集した分布になるはずだ」という想定によります。図でいうと3つAverageLandPriceが特に大きいものがありますが、これらは例えば東京都中央区や港区などの地価が高いエリアであると想定されます。

with Year

sns.scatterplot(data=train, x='AverageLandPrice', y='Year')
plt.show()

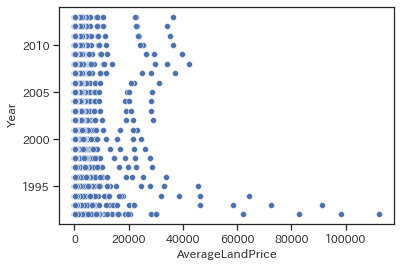
影響の大小はありそうですが概ね年次が上がるほど下がる傾向にあるようです。1992年あたりはバブルだったことを考えると、当然でしょうか。

with MeanLight

sns.scatterplot(data=train, x='MeanLight', y='AverageLandPrice')
plt.show()

​

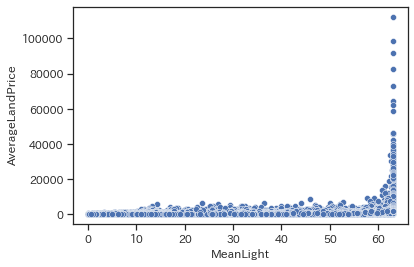
完全ではありませんが傾向としてMeanLightが大きいほど地価も高そうです。特に最大値63近辺で顕著です。夜間光量の平均値が高い（＝電気がギラギラ）なほど地価が高いというのは一般的な感覚とも合致します。

with SumLight

sns.scatterplot(data=train, x='SumLight', y='AverageLandPrice')
plt.show()

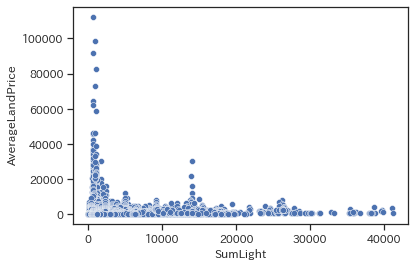
今度はどちらかというとMeanLightとは逆の結果になりました。合計光量が少ないほど地価が高く、多いほど地価が安い傾向が見られます。SumLightが大きい->MeanLightが大きいとも考えられますが、別の場合を考えると平均的な光度は小さくとも単に面積が広い場合が考えられます。都市ほど地価は高くても面積が狭い傾向にありますので、その傾向の現れと思われます。

with area

データの概要で触れた通り、SumLightをMeanLightで割ったものはその地域の面積を表すと思われます。その値とAverageLandPriceの関係も見てみます。

train['area'] = train['SumLight'] / train['MeanLight']

sns.scatterplot(data=train, x='AverageLandPrice', y='area')
plt.show()

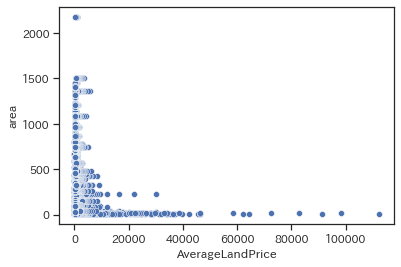
やはり基本的には面積が小さいほど地価が高い傾向にありそうです。ただし島村部など面積も地価も小さい箇所も混ざっているはずなので、必ずしもそうでもないため扱いに悩むところです。今回は実装しませんが、例えばMeanLightと合わせて考えてみることで「狭いけど栄えている街」を表す特徴量が作れるかも知れません。

特徴量エンジニアリング

方針

いきなり特徴量を作成する前に、EDAを通して見えてきたことをまとめつつ、どんな特徴量を作成するかまとめておきます。

PlaceID

• trainとtestで被っていないため、そのまま使用するのは危険そうです。
  • 特定できる方法で特徴量化してしまうと、交差検証の際に不当に高いスコアがでてしまう可能性があります。
  • 詳しくは交差検証の際に後述します。
  • PlaceIDを特定せずに特徴量化する方法として、ここではCountEncodingで変換することにします。
  • ほとんどがデータがある年次分の値（=22）になってしまいますが、一部全年次分のデータがない地域があるため多少の差が付きます。
  • 反対に、仮にCountした数がバラバラですと結局CountEncodingをしてもその数の違いによってPlaceIDを特定できてしまいます。CountEncodingが常に元の値を特定できないようにする変換方法ではないことに注意してください。

Year

• 影響の大小はありそうですが、傾向としてはバブルの影響か年次が上がるほど地価が下がる様なので、そのまま特徴量化します。
  • 今回使用するアルゴリズムは決定木系統のため、大小関係がついていれば変換の必要なく使用できます。
  • 決定木系統のアルゴリズムの場合は大小関係の変わらない変換は不要という点（と、そうとも限らない点）については、こちらのブログ記事などをご参考ください。
  • 今回は実装しませんが、Yearの影響を受けやすい地域とそうでない地域（バブルで地価が崩壊した地域とそこまで影響がなかった地域）を何かしらの方法で分類し、その分類別に年次をスコア化した特徴量なども効果的かもしれません。

MeanLight

• そのまま使います。
• いくつか、PlaceID単位で各種統計値を特徴量化します。
• また、63の値となる地域は特に地価が高い傾向にあったため、この情報も抜き出したいと思います。
  • 色々やり方あると思いますが、今回は「値が63になった回数」で表現したいと思います。
  • 22年間63を取り続ける地域と、何回か63もあるけど62...もある地域との差を表現したいと考え、一つの方法として選びました。

SumLight

• そのまま使います。MeanLightとareaと情報が被っている気もしますが、今回使用するGBDT系のモデルは多少無意味な特徴量が含まれていても精度が落ちにくい傾向にあるため（詳細はkaggle本6.2などを参照ください）、とりあえず入れてみます。
• MeanLight同様、いくつかPlaceID単位で各種統計値を特徴量化します。

area

• SumLightをMeanLightで割って算出します。
• 面積のはずなのに、同じ地域でも小数点以下程度でズレが生じるので地域ごとの中央値に置き換えます（おそらく配布データの桁数の問題？）。

特徴量作成

ではいよいよ特徴量を作っていきましょう！
まずは、特徴量作成に便利なライブラリをimportしつつ、EDAの時に色々といじくって余計な情報を加えてしまったのでtrainとtestを読み込みなおしておき、比較的簡単な特徴量を作成していきます。このとき、今回はtrainとtestを別々に処理してもまとめて処理しても結果が変わらない特徴量しか作成していないため、コードを短く済ますために最初にtrainとtestを結合してまとめて特徴量を作成しています。しかし場合によってはtrainとtestは別々のまま作るべき特徴量もあれば、まとめて作るべき特徴量もあります。

※category_encodersの使い方はこちらのQiita記事などを参照ください。

import category_encoders as ce # CountEncodingなどカテゴリ変換に便利なライブラリ

train = pd.read_csv(os.path.join(DATA_DIR, 'TrainDataSet.csv'))
test = pd.read_csv(os.path.join(DATA_DIR, 'EvaluationData.csv'))
df = pd.concat([train.drop('AverageLandPrice', axis=1), test], ignore_index=True)

# PlaceIDのCountEncoding
enc = ce.CountEncoder(cols='PlaceID')
df['count_PlaceID'] = enc.fit_transform(df)['PlaceID']

# 面積の計算
df['area'] = df['SumLight'] / df['MeanLight']

# 面積なのに同じ地域でも年次によって小数点以下でズレが生じるため、地域ごとの中央値に置き換える
_mapping = df.groupby('PlaceID')['area'].median()
df['area'] = df['PlaceID'].map(_mapping)

# 面積について、SumLightとMeanLightがともに0な地域があり、NaNになってしまうので0で補完する
# 完全に光が無い闇の地域？引用元でのデータ取得時のエラーが原因？
df['area'] = df['area'].fillna(0)

# 各地域でMeanLightが63をとった回数を特徴量にする
_mapping = df[df['MeanLight']==63].groupby('PlaceID').size()
df['count63'] = df['PlaceID'].map(_mapping)

# MeanLightが一回も63になっていないとNaNになってしまうので0で補完する
df['count63'] = df['count63'].fillna(0)

---

2/19 19:26追記

上記のコードでareaとcount63の欠損値を0で補完していますが、LightGBMは欠損値があっても処理をして訓練・予測を行ってくれます。「LightGBMも欠損値処理しないと訓練できないのか」と誤解されませぬと幸いです。「その処理とは何ぞや」については大変申し上げにくいのですが私も完璧には理解できておらず、英語ですがこちらのLightGBMのissueが参考になるかと思います。

とてもざっくり言うと欠損値があってもエラーを出さないように欠損値なりの分岐をするようになっており、今回のコードで補完している箇所の値を変えると以下の様にCVスコア（後述の予測の項で算出しています）が変化します。黄色の両方0で補完しているのが本記事での結果です。

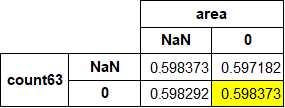
上記の通り実は両方0で補完した場合とNaNで補完した結果は変わらないのですが他の組み合わせでよりCVスコアが良いものもあります（あくまで今回の状況においてはこうなったという話で常にこうなるわけではありません）。じゃあなんでお前はわざわざ0で補完したのかというと…

• count63：MeanLightが63になった回数なので「0回」と明示的に表すことに意味があると思った
• area：0除算なので計算できないが、MeanLightとSumLightが両方0なのはなにかエラーが起きていそう->元となった数値のエラーを0としている（と思われる）なら、その結果も0にしておくと良いのかも知れない

と考えたことによります。コンペにおいて上位に入ることを目指すのであれば、（Privateと相関していると信じられる）交差検証の結果を見ながら処理を決めるのが良いかと考えています。

---

これでシンプルな特徴量はできましたが、少し作成に手間がかかる特徴量も作ってみます。冒頭のメモで触れていた「PlaceID単位のMeanLightとSumLightの各種統計値」というもので、pandasのgroupbyメソッドを使って作成します。基本的な統計量はデフォルトの関数を利用できますが、少し凝った統計量も関数を自作して適用します。

# 最小値と最大値の差
def range_diff(x):
    return x.max() - x.min()

# 第一/三四分位点とその差
def third_quartile(x):
    return x.quantile(0.75)
def first_quartile(x):
    return x.quantile(0.25)
def quartile_range(x):
    return x.quantile(0.75) - x.quantile(0.25)

# 集計
cols = ['MeanLight', 'SumLight']
aggs = ['min', 'mean', 'median', 'max', 'std', 'skew',
        range_diff, third_quartile, first_quartile, quartile_range]
_df = df.groupby('PlaceID')[cols].agg(aggs).reset_index()

# 列名変更のため、aggsの各名称を_aggsに格納
_aggs = []
for agg in aggs:
    if isinstance(agg, str):
        _aggs.append(agg)
    else:
        _aggs.append(agg.__name__)

# 列名変更
_df.columns = ['PlaceID'] + ["_".join([c, agg]) for c in cols for agg in _aggs]

ここまでの処理で、以下の様なPlaceID毎のMeanLight、SumLightの各種統計量をまとめたDataFrameができました。あとはこれを元のDataFrameにPlaceIDをキーにmergeします。

_df.head()

	PlaceID	MeanLight_min	MeanLight_mean	MeanLight_median	MeanLight_max	MeanLight_std	MeanLight_skew	MeanLight_range_diff	MeanLight_third_quartile	MeanLight_first_quartile	...	SumLight_min	SumLight_mean	SumLight_median	SumLight_max	SumLight_std	SumLight_skew	SumLight_range_diff	SumLight_third_quartile	SumLight_first_quartile	SumLight_quartile_range
0	1	6.654412	9.578523	9.625000	12.708955	1.219428	0.101592	6.054543	10.244485	9.016956	...	905.0	1299.818182	1305.0	1703.0	163.160055	0.004118	798.0	1393.25	1221.25	172.00
1	2	41.154762	48.058121	48.285715	53.911243	3.037256	-0.471909	12.756481	49.413692	47.144344	...	6914.0	8080.590909	8112.0	9111.0	515.614442	-0.436319	2197.0	8301.50	7920.25	381.25
2	3	6.647059	9.794118	9.808824	12.735294	1.582701	-0.064804	6.088235	10.963236	8.669117	...	226.0	333.000000	333.5	433.0	53.811842	-0.064804	207.0	372.75	294.75	78.00
3	4	28.584158	36.124792	35.789603	44.330048	3.660401	-0.062634	15.745890	38.267328	34.143565	...	5774.0	7302.681818	7229.5	8999.0	746.146761	-0.032737	3225.0	7730.00	6897.00	833.00
4	5	41.631580	49.547581	49.368420	55.777779	3.309324	-0.578802	14.146199	51.868420	48.381578	...	791.0	934.181818	935.5	1027.0	57.405522	-0.777810	236.0	972.50	917.50	55.00

5 rows × 21 columns

# 元のDataFrameにmerge
df = df.merge(_df, on='PlaceID', how='left')

訓練・予測

いよいよ訓練＆予測です！ここまでに比べると長いコードですがkaggleスタートアップ本を参考に書いております。自分もコンペ初参加時はとても参考にした本ですので、お持ちでない方は是非是非読んでみてください！
ここではlightgbmの説明は省かせて頂きますが、2点補足いたします。

y_trainを対数変換する理由

lightgbmのobjectiveには今回の評価指標であるRMSLEがなく、最適化するためには自分で関数を作成するなどの対応をとる必要があります。それはちょっと面倒なので「対数変換したものをy_trainとしてRMSEで最適化して、あとで元のスケールに戻す」という方法が良く取られます。対数変換せずにいきなりRMSEで最適化するのがよろしくない理由はこちらの記事を、具体的にどうやって変換するかは以下のコードの通りですがこちらのQiita記事などもご参考ください。

バリデーション方法をGroupKFoldにしている理由

EDAで見た通り、trainとtestではPlaceIDが一切被っていません。順当に考えればPlaceIDが同じ場合の地価は似たような値になるはずで、例えば訓練時に「各地域の1992年~～2010年の情報を使って学習して2011年～2013年を予測し評価する」としてしまうとtestの時にはできないカンニングをしていることになり、不当に高いスコアとなり正当な評価ができなくなってしまいます。そのため、できるだけ条件をtestを予測する際と合わせるために訓練データと検証データでPlaceIDが混ざらないようにGroupKFoldを選んでいます。

x_train = df[:len(train)].drop('PlaceID', axis=1).reset_index(drop=True)
x_test = df[len(train):].drop('PlaceID', axis=1).reset_index(drop=True)
y_train = np.log1p(train['AverageLandPrice'])

import lightgbm as lgb
from sklearn.model_selection import GroupKFold

y_preds = []
models = []
oof_train = np.zeros((len(x_train),))
cv = GroupKFold(n_splits=5)

params = {
    'objective': 'rmse',
    'learning_rate': 0.01,
}

for fold_id, (train_index, valid_index) in enumerate(cv.split(train, y_train, train['PlaceID'])):
    X_tr = x_train.loc[train_index, :]
    X_val = x_train.loc[valid_index, :]
    y_tr = y_train.loc[train_index]
    y_val = y_train.loc[valid_index]

    lgb_train = lgb.Dataset(X_tr, y_tr)
    lgb_eval = lgb.Dataset(X_val, y_val, reference=lgb_train)

    model = lgb.train(params, lgb_train,
                      valid_sets=[lgb_train, lgb_eval],
                      verbose_eval=100,
                      num_boost_round=10000,
                      early_stopping_rounds=100)

    oof_train[valid_index] = \
        model.predict(X_val, num_iterations=model.best_iteration)
    y_pred = model.predict(x_test, num_iterations=model.best_iteration)

    y_preds.append(y_pred)
    models.append(model)

Training until validation scores don't improve for 100 rounds
[100]   training's rmse: 0.615957   valid_1's rmse: 0.646416
[200]   training's rmse: 0.445885   valid_1's rmse: 0.578616
[300]   training's rmse: 0.371811   valid_1's rmse: 0.575487
Early stopping, best iteration is:
[270]   training's rmse: 0.389244   valid_1's rmse: 0.574996
Training until validation scores don't improve for 100 rounds
[100]   training's rmse: 0.619655   valid_1's rmse: 0.675378
[200]   training's rmse: 0.451198   valid_1's rmse: 0.592721
[300]   training's rmse: 0.377045   valid_1's rmse: 0.574313
[400]   training's rmse: 0.333679   valid_1's rmse: 0.571923
[500]   training's rmse: 0.300587   valid_1's rmse: 0.572853
Early stopping, best iteration is:
[460]   training's rmse: 0.313101   valid_1's rmse: 0.57166
Training until validation scores don't improve for 100 rounds
[100]   training's rmse: 0.60571    valid_1's rmse: 0.773037
[200]   training's rmse: 0.439709   valid_1's rmse: 0.67063
[300]   training's rmse: 0.368091   valid_1's rmse: 0.652486
[400]   training's rmse: 0.324932   valid_1's rmse: 0.649166
Early stopping, best iteration is:
[393]   training's rmse: 0.327592   valid_1's rmse: 0.648902
Training until validation scores don't improve for 100 rounds
[100]   training's rmse: 0.613064   valid_1's rmse: 0.687336
[200]   training's rmse: 0.446505   valid_1's rmse: 0.585084
[300]   training's rmse: 0.372544   valid_1's rmse: 0.5676
[400]   training's rmse: 0.329101   valid_1's rmse: 0.568454
Early stopping, best iteration is:
[329]   training's rmse: 0.358066   valid_1's rmse: 0.566874
Training until validation scores don't improve for 100 rounds
[100]   training's rmse: 0.607628   valid_1's rmse: 0.725103
[200]   training's rmse: 0.438502   valid_1's rmse: 0.643018
[300]   training's rmse: 0.36519    valid_1's rmse: 0.633235
[400]   training's rmse: 0.322654   valid_1's rmse: 0.630308
[500]   training's rmse: 0.289557   valid_1's rmse: 0.629517
[600]   training's rmse: 0.2642 valid_1's rmse: 0.630763
Early stopping, best iteration is:
[510]   training's rmse: 0.286657   valid_1's rmse: 0.629432

scores = [
    m.best_score['valid_1']['rmse'] for m in models
]
score = sum(scores) / len(scores)
print('===CV scores===')
print(scores)
print(score)

===CV scores===
[0.5749961295452265, 0.5716597018095386, 0.648901926064152, 0.5668740744440104, 0.6294317310106663]
0.5983727125747187

ここまではkaggleスタートアップ本の通りです。スタートアップ本の分類の例と異なり今回は回帰問題ですので、各modelの予測結果の平均を最終予測とします。※y_trainを対数変換したのでy_predも対数スケールでの予測結果です。スケールを戻すのを忘れずに！

y_pred = 0
for pred in y_preds:
    y_pred += np.expm1(pred) / len(y_preds)

投稿の前にあまりに的外れな予測をしていないか、正解であるy_trainとout-of-foldの予測結果が似たような分布になっているか確認してみます。

fig, ax = plt.subplots(figsize=(8, 8))
sns.histplot(y_train, label='y_train', kde=True ,stat="density", common_norm=False, color='orange', alpha=0.3)
sns.histplot(oof_train, label='oof_train', kde=True, stat="density", common_norm=False, alpha=0.3)
ax.legend()
ax.grid()

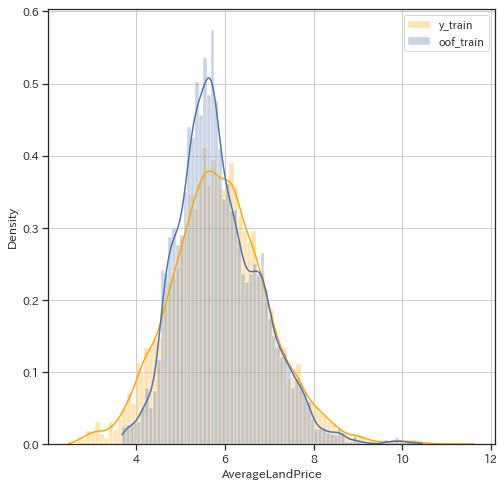
予測結果の方が真ん中に寄った分布になってしまってはいますが、極端なズレはないためひとまずそれらしい予測はできたと見て予測ファイルを作成し投稿します。ちなみにこちらの結果を投稿するとPublicLBで0.551596のスコアになります。

# 予測ファイルの作成
submission['LandPrice'] = y_pred
submission.to_csv('submission.csv', index=False)

さいごに

以上、予測を作成し投稿する一連の流れの一例を紹介しました。データの捉え方、特徴量の作り方、アルゴリズムの選び方などなど…これだけが正解ではもちろんないですが、この記事がデータ分析コンペ参加にハードルを感じている方の後押しとなれば幸いです。