高校生に向けた生物物理班紹介

挨拶

初めまして。Physics Lab. 2025の暫定的生物物理班班長です。高校生にも伝わることを試行して、「高校生に向けた生物物理班紹介」というタイトルで書かせて頂きます。

記事の内容は学生個人の見解であり、所属する学科組織を代表するものではありません。

脚注が多いのですが、読み進めるうえでは一々参照しなくても大丈夫です。

参考にしようと思って「高校生　生物物理」と検索してみたのですが、「生物物理学」ではなく「受験で生物を使うか、物理を使うか」の記事ばかりが出てきます。逆に言えば、物理や生物を専門的に大学で学んでいなければ、両者は一見交わり難いものだと思われていそうです。

それを踏まえて、本記事では

i) 高校物理選択者に向けた説明
ii) 高校生物選択者に向けた説明
iii) 膜の等価回路モデルの紹介
と分けて生物物理を紹介します。¹²

i) 高校物理選択者に向けた説明

もしあなたが、高校3年生なら、この時期までに初等的な力学、波、電磁気を高校で習った人も多いかと思います。大学入試対策で複雑な設定の問題を解いたりしているかもしれません。
しかし、原子核とか光の波の干渉、帯電させたコンデンサを十分ゆっくり動かしては帯電させたり、と一見、「それがわかったところで何が嬉しいのか？」となるような問題も多いと思います。³
暗記が比較的少ないからという消極的な理由で物理選択にしている人もいると思います。⁴
しかし、もし、物理を使って身近なもの・一見理解しがたいものを理解⁵できたら嬉しいと思いませんか？
私は大学1年生の5月、東大五月祭のPhysicsLab. 2022で「生物物理」に出会いました。私が観たポスターは、統計力学を使って高分子がどれくらいの広がり⁶を持っているのか求めるという内容でした⁷⁸。勿論、化学的な相互作用やモノマーの形状のような実態を無視したモデルではありますが、まさに複雑で博学的な生物という分野に対しても「物理が使えるんだ」ということに感銘を受けました。
この例だけだと、面白そうに聞こえないという方もいると思います。他の例として、電磁気を使った細胞膜の一つのモデル化である「膜の等価回路モデル」の紹介を後ろに載せています。もし、興味を持っていただけたら幸いです。もし、あまり面白いと思っていただけなくても、生物物理は対象とする現象・使う物理が多岐にわたるので、興味を持っていただけるものもあるかもしれません。

ii) 高校生物選択者に向けた説明

細胞の構造、代謝、遺伝子の働き、各器官の仕組み、生殖、環境応答等、生物集団、進化などかなり幅広いことを高校の生物で扱うと思います。大学受験の対策上は、暗記が他の理科教科に比べて桁違いに多いでしょう。⁹
では、これはなぜでしょうか？
私は、生物分野で「定理」と呼ばれるような統一的見解を与えるものがほとんどないことが一因だと思います。確かに生物において定義を作るにも生物が多様・複雑すぎて反例が簡単に見つかってしまうことが多そうです。¹⁰それゆえ、「いつ・どこで・何が・どうやって」という質問だけでなく、「なぜ」という問いにも只管生物学的な実験結果から個別に理解するしかなさそうに思われます。しかし、本当に生物に対してはそのような博学的な理解の仕方しかないのでしょうか？
数理モデルからなにか生命現象について言えることがないか？という（強いて言うなら）トップダウン的な営みとして、理論生物学・システム生物学・数理生物学¹¹等があります。
そのうち、物理的知見にベースを置く部分・あるいは(数理モデルの話とは逸れますが)物理的手法を用いて生物を研究している分野が生物物理学です。
学際的な分野であるがゆえに、境界を引くのは難しく、逆に言えば幅が広いです。
生物物理学夏の学校(生物物理学を研究している大学院生中心のイベント)のトピックをいくつか観てみると、

• 細胞・基質間のカップリング
• 化学反応ネットワーク(代謝系など)
• 遺伝子変異に対する頑強性
• 培養神経系の神経活動
• 生命の老化メカニズム
• バクテリアの集団運動
  など、高校生物の各トピックと対応するような研究がたくさんあります。

iii)膜の等価回路モデル

細胞は二重の細胞膜という膜で外界と隔てられています。
この膜は　水に馴染みやすい部分と馴染みにくい部分を持つ分子(リン脂質)からできていて、水に馴染みにくい部分を膜の内部に留めるような向きで並んでいます。

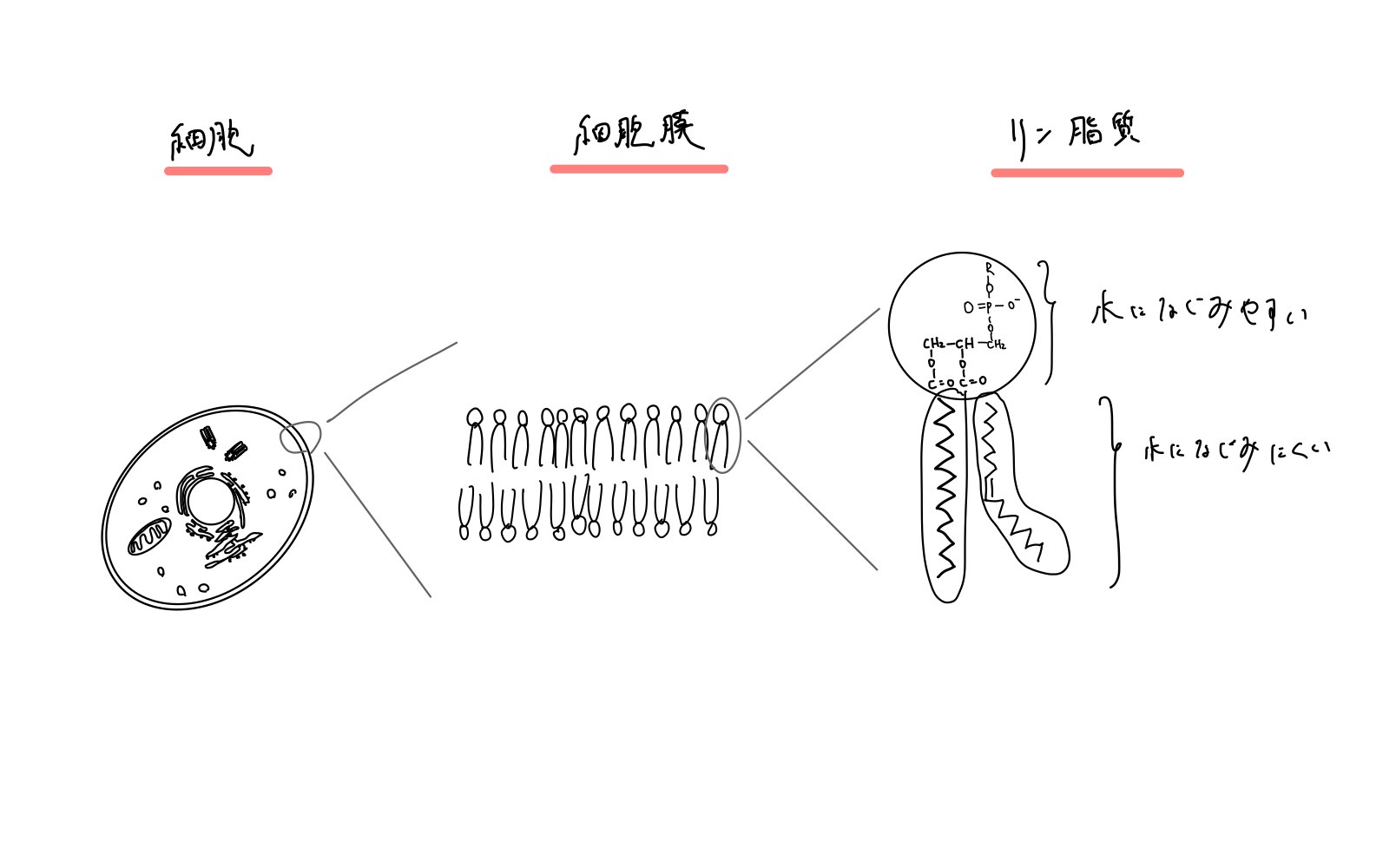
つまり、分子が細胞膜を直接通るには水に馴染みにくい部分を通過できなければならないわけです。
水に馴染みやすい=電荷をもつものを通しやすい
水に馴染みにくい/油に馴染みやすい(疎水性)=電荷をもつものを通しにくい
ということから
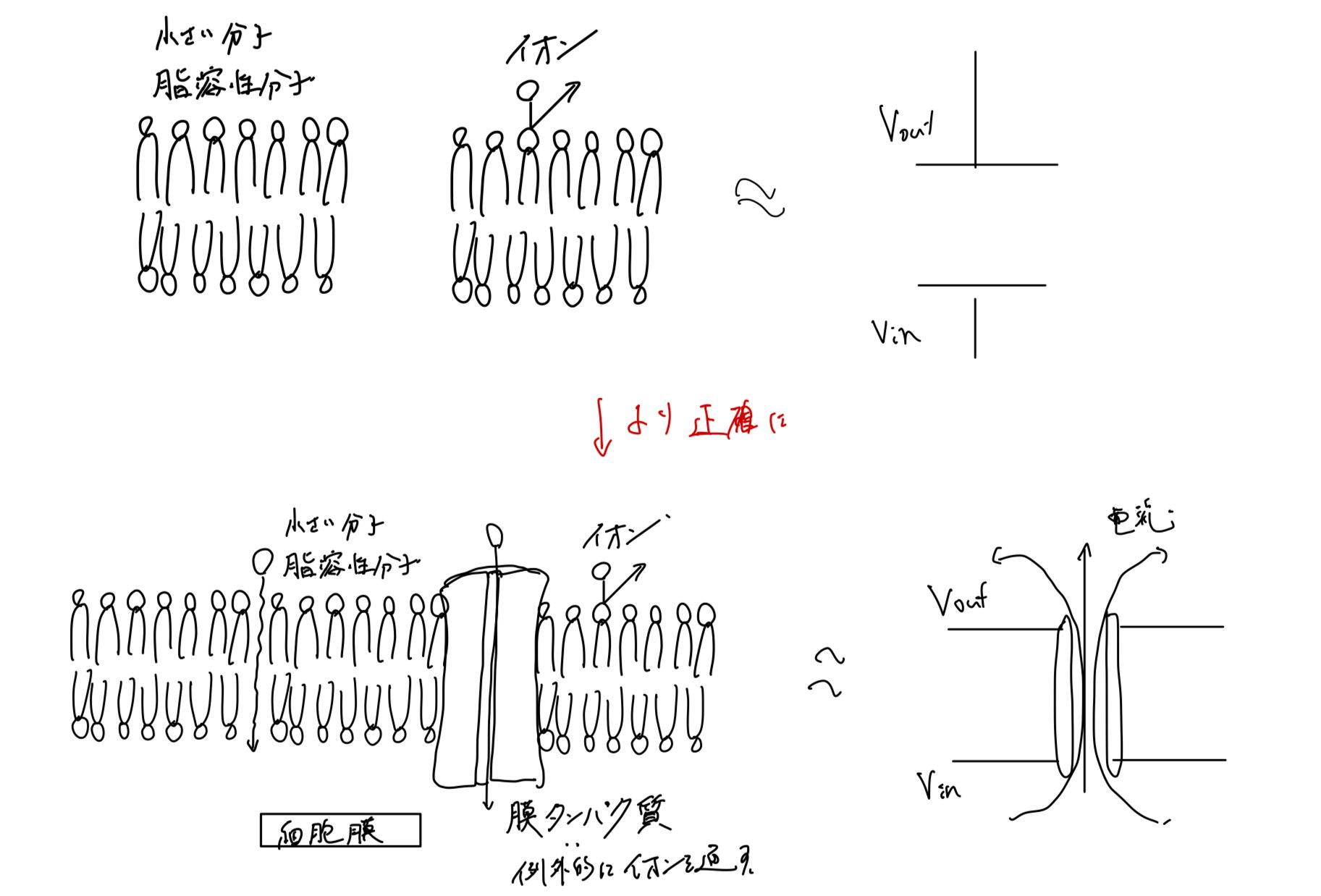
小さい分子・脂溶性分子は細胞膜を通過して細胞内外でやり取りされる一方、イオンは膜を非常に通りにくいことがわかります。

言い方を変えれば、細胞膜は電荷を分けます。
もしかしたら、ピンと来た方がいるかも知れません。これは、コンデンサだとみなせます。

では、生物は細胞内外でイオンをやり取りしないのでしょうか？
答えは、いいえです。もし、イオンをやり取りしなければ、神経活動はなくなってしまうし、エネルギー(ATP)も生成できません。
どうやって、イオンをやりとりしているのでしょうか？

先程の細胞膜の紹介では不十分で、実は細胞膜にはイオンを輸送するようなタンパク質があります。イオンの輸送はエネルギーを消費し濃度勾配に逆らうもの(能動輸送)と濃度勾配に従うもの(受動輸送)があります。
今回は、細胞膜に受動輸送するようなタンパク質(イオンチャネル)がある場合を考えてみましょう。
イオンチャネルはイオンを通します。電荷がイオンチャネルを通っているとも言えるわけです。したがって、ある種の電流（イオン電流）が流れているといえます。

ここまでを振り返ると、イオンチャネルが突き刺さった細胞膜は、電流を通すような穴が空いたコンデンサだとみなせます。

しかしこのままでは電磁気学で扱いにくいので、ひとまずイオンの出入りの流れが時間的に変化しないという仮定をして単純化しましょう。
僅かながら脂質二重膜を通るイオンの流れがあるのでこのイオン電流を$I_{cap}$、
イオンチャネルを通るイオン電流を$I_{ion}$とします。電流は合わせて$I_m=I_{ion}+I_{cap}$です。

(i) $I_{cap}$について
$I_{cap}$は先程の考えに基づくとコンデンサを通っていることになります。コンデンサではコンデンサにかかっている電圧を $V$ 、コンデンサの静電容量を$C$、蓄えられている電荷を $Q$ とすると、
$CV=Q$
でした。
これと同様に、短い時間 $\Delta t$ の間に電流 $I_{cap}$ がコンデンサを通るとコンデンサに蓄えられる電荷は $I_{cap}\Delta t$ だけ増えます。
それに依って、コンデンサにかかる電圧も $\Delta V$ だけ増えているはずです。
この関係はさきほどの $C V=Q$ と見比べると、
$ C\Delta V=I_{cap}\Delta t $
あるいは

C\frac{\Delta V}{\Delta t}=I_{cap}

です。$\Delta t$をどんどん0に近づけると、左辺は数学で考えた「微分」になって
$\frac{dV}{dt}=\frac{I_{cap}}{C}$
あるいは

C\frac{dV}{dt}=I_{cap}

です。
(ii) $I_{ion}$について
チャネルを電荷は導線を通るようにスムーズに通るのでしょうか？
通れる量は限られていて、どちらかというと抵抗とみなすほうが良さそうです。
さらに、イオンの濃度勾配によって電圧差$E_{eq}$があります。
これを$E_{eq}$とすると、膜にかかっている電圧から$E_{eq}$を引いただけの電圧が抵抗にかかっているとわかります。
つまり抵抗値をRとするなら

V-E_{eq}=I_{ion}R

とかけるでしょう。

(i)と(ii)を合わせると、
下のような回路とみなせます。

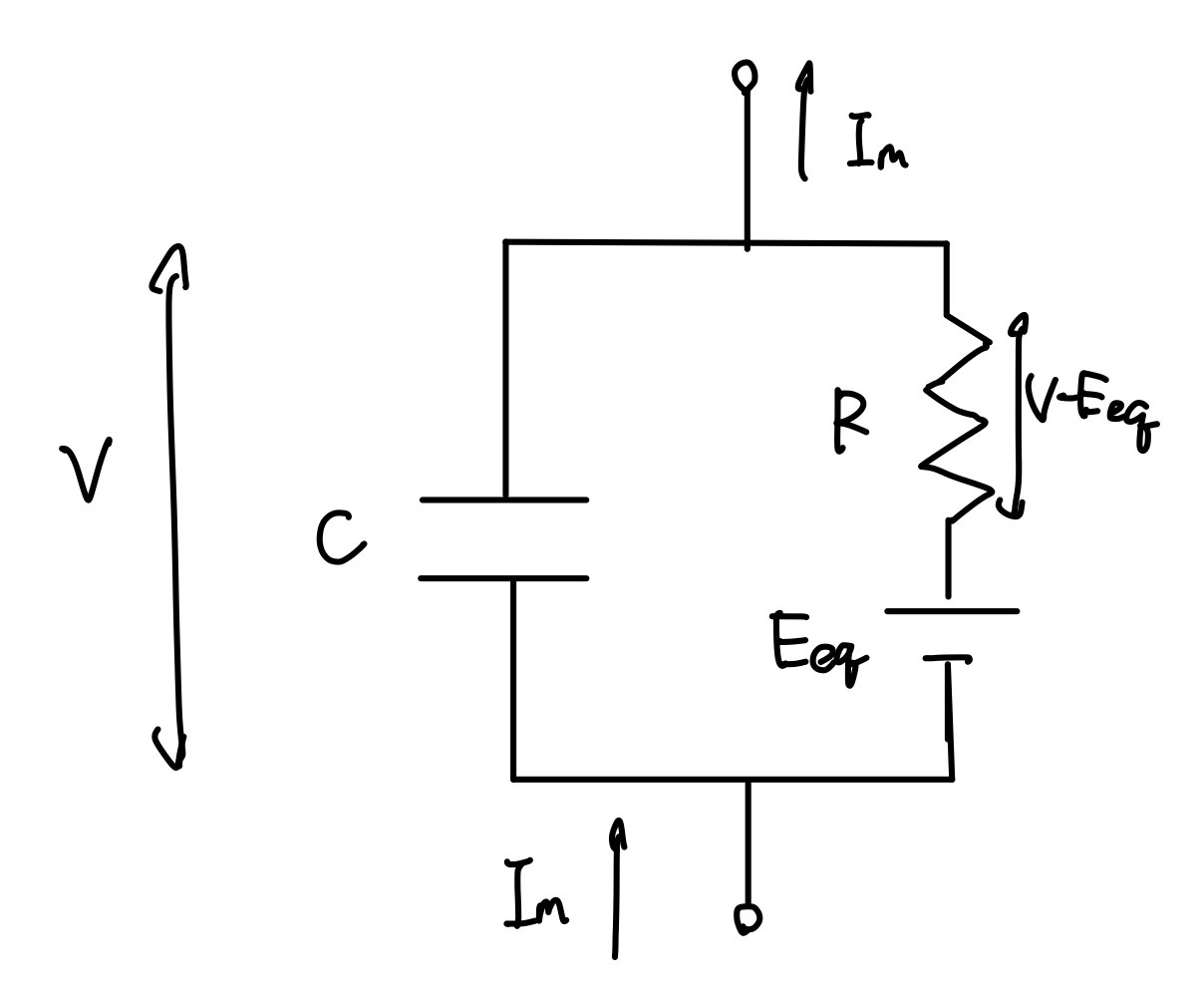
式としては

I_m=C\frac{dV}{dt}+\frac{1}{R}(V-E_{eq})

とかけました。

微分が入っていてよくわからないと思われるかもしれません。実際、$I_m$
も時間変化する場合は考えにくいのですが、Vについてのこの微分方程式を解くと電流が供給されない
$I_m=0$のときならば、

V=(V_0-E_{eq})e^{-\frac{t}{RC}}+E_{eq}

になって、図のように時間が経つと$E_{eq}$に近づくことがわかります。

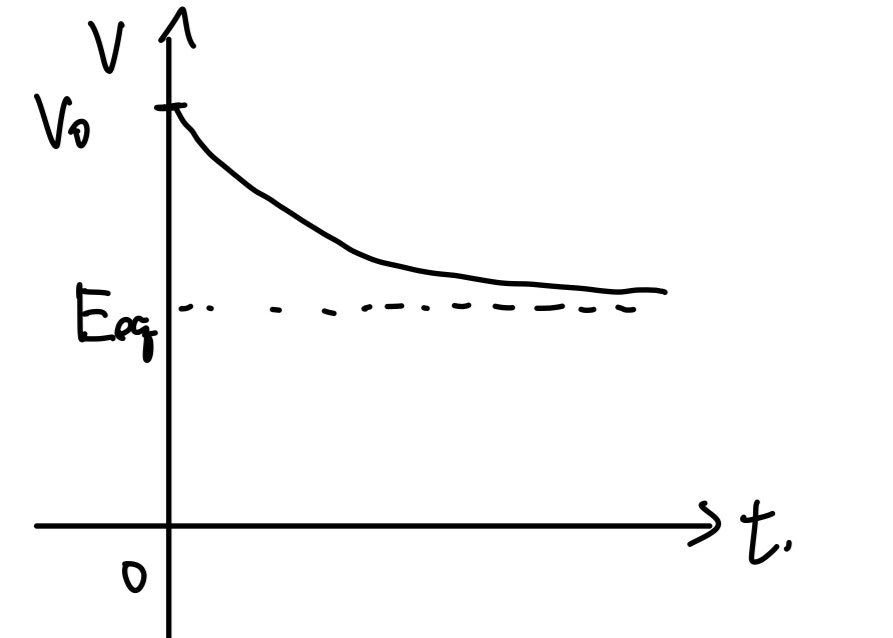
今回は$E_{eq}$や$R$がどうやったら求まるのか、また$E_{eq}$の詳しい意味を省略しましたが、実は大学の最初に学ぶ熱力学の範囲で十分に式を理解できます。

最後に

一般の生物物理班紹介、あるいは自分で生物学的事象についてモデルを立てて考えてみる記事も上げる予定です。
これをきっかけに、Physics Lab.や生物物理に関心を抱いていただけると幸いです。

参考文献

[I] 清水明 (2024), 統計力学の基礎 I,東京大学出版会
[II] 清水明, 東京大学 教養学部 １，２年生向け講義 (Aセメスター，金曜5限）
統計物理学 2022 (参照: https://as2.c.u-tokyo.ac.jp/lecture_note/)

[III] 宮川 博, 井上 雅 (2003), ニューロンの生物物理,  丸善出版

1. 調べてみると、高校物理生物選択者による近い観点での説明が
   https://note.com/shino_gen_3141/n/n7c816a32f664
   という記事に含まれているようです。興味のある方は是非読んでみてください。 ↩

2. 物理化学選択だった私に語る権利はあるのか？という気もしますが、大学2年生のときに高校生物を個人的に1周したことを免罪符にさせてください。真面目に答えるならば、生物選択の人にも、本記事で生物物理に興味を持ってもらえたら幸いです。 ↩

3. 勿論、私が高校生の時につまらないと思っていた問題のうち大学生になってからその意味をちゃんと理解したものも多いです。(例:2011年東大大問2のコッククロフト・ウォルトン回路; 高電圧を得るためにたくさんコンデンサを並列していると問題に書いてあるのですが、当時はその重要性がわからなかったです。) ↩

4. 批判的な意図ではなく、実際私も生物選択か物理選択かを決めるときに暗記の少なさを一つの理由にして物理を選びました。 ↩

5. 「理解」と書きましたが、物理は近似理論に過ぎないことには留意が必要です。例えば斜面を落ちる球の加速度を調べるような初等的な実験でも誤差は付き物ですし、高校範囲でも$|x|$が小さいなら$\sqrt{x+1}\approx1+\frac{x}{2}$のような近似をしばしば使います。一方で、自然の複雑さを前に何もしないのではなく、少しでも知るために近似を使って理解しようとすること自体は有意義だと思います。近似で得られた理論と実験が必ずしも一致するとは限りません。しかし、実験と理論の比較に依って理論を検証したりあるいは実験結果から理論への知見を得るという営みで世界を理解するのは他の物理分野あるいは科学全般と同様だと思います。(ここでの主張は[I]の文献の第一章あるいはその内容を扱った2022 Aセメスター　統計物理学の授業に影響を受けています。) ↩

6. 例えばタンパク質は1次元的にアミノ酸が連なっているわけですが、水溶液中、あるいは体内では折りたたまれて2次・3次構造が形成されているため、分子鎖としての長さと実際の構造の半径のようなものは明らかに違うはずです。 ↩

7. このポスターは今でもネット上で閲覧することが可能です。(https://event.phys.s.u-tokyo.ac.jp/physlab2022/poster/bp-poster02.pdf) ↩

8. 流石にポスターだけで理解できるほど、(特に当時、応用化学系に進むつもりでいた私にとっては)簡単ではありませんでしたが、その場にいた物理学科の方を捕まえて質問したところ、解説講義をしてくださったのも含めて非常にありがたい経験でした。 ↩

9. 特に解糖系・クエン酸回路・電子伝達系の部分は本当に覚えられなくて苦しかったというのを今でも覚えています。一方で、生物で受験した友人(例えば　https://note.com/downer_angel) は「東大生物に生物の知識は要らない」ということを言っています。私は、東大生物には日本語読解力も必要だと思うのですが、流石に実用上は、生物の知識を揃えていないと時間内に全然記述が終わらないとも思うので、完全にその意見に賛成することはできません。 ↩

10. 例えば、定理的なものとして知られる「セントラルドグマ」には遺伝子発現にフィードバックを与えるようなmiRNAが反例として挙げられます。配列のみから構造がわかると主張する「アンフィンセンのドグマ」についても、プリオンというタンパク質は正常形と異常形で同じ配列なのに構造が違うという反例があります。 ↩

11. これらの明確な違いについては、よくわかりません。 ↩