自作言語の型システムの話 #型

この記事は言語実装 Advent Calendar 2018 の20日目です.

今ブログエンジンを自作しているんですが, もしこの記事が Qiita で公開されているなら¹, 間に合わなかったということです.

プログラミング言語と現実世界

プログラミング言語²において, 現実世界における計算順序の定め方は大体次の2種類に分かれる³.

ML 方式

操作的意味論における評価戦略で計算順序を定めてしまう方式. 利点は設計も実装もめちゃくちゃ単純で考えることがほぼないこと. 欠点は最適化のためのコード変形がとてつもなく大変なこと. 例えば,

let x = Scanf.scanf "%s" in (x, x)

のようなコードを

(Scanf.scanf "%s", Scanf.scanf "%s")

のように変形するだけで動作が変わってしまう.

Haskell 方式

言語の中では計算順序を 定めない. 実際にどう動作させるかはコンパイラが決める. 利点は設計が超簡単な上, やろうと思えば合流性⁴など様々な嬉しい性質をもたせられること. 欠点は実装が超大変で考えることが多いこと.

具体的な実装として GHC を挙げる. GHC では現実世界との相互作用を行なう IO モナドは次のように定義されている⁵.

type IO a  =  RealWorld -> (a, RealWorld)

つまり, RealWorld を状態とした State モナドの一種である. しかし, これは現実世界のモデルとしてはある意味 壊れている. なぜなら, GHC は RealWorld 型の値をユーザに一切触らせないようにすることでプログラム実行の線形性を担保しているからだ. もし触れたとしたら, 値をコピーすることで現実世界を分裂させたり, なかったことに したり, 過去に戻って やり直したりできてしまう. acme-realworld はこのモデルのおかしさをうまく突いたジョークパッケージで, GHC の内部関数を使ってそれを行えるようにする⁶.

線形時相論理

両者のいいところ取りをするにはどうすればいいのだろうか. 言語の持つよい性質を保ちつつ, 現実世界における計算の発生順序をきちんと言語内で扱うには, やはり, 言語のカリーハワード先の体系自体に現実世界を扱う能力を持たせるのが手っ取り早い.

それにぴったりなのが 線形時相論理 (Linear Temporal Logic, LTL) だ. 現実世界は線形, つまり分裂したりループしたり合流したりしないので, 線形な時間経過しか表せない LTL でも十分事足りる.

LTL の推論体系 $\mathscr{L}$ を以下で定める⁷.

論理式: 命題論理の論理式 + 単項演算子 $\circ, {\small \Box}, \diamond$

公理: 命題論理の公理 +

${\small \Box}$ の分配: $\vdash {\small \Box} (A \rightarrow B) \rightarrow ({\small \Box} A \rightarrow {\small \Box} B)$
$\circ$ の分配: $\vdash \circ (A \rightarrow B) \rightarrow (\circ A \rightarrow \circ B)$
${\small \Box}$ の展開: $\vdash {\small \Box}A \rightarrow (A \wedge \circ A \wedge \circ {\small \Box} A)$
帰納: $\vdash {\small \Box}(A \rightarrow \circ A) \rightarrow (A \rightarrow {\small \Box} A)$
線形性: $\vdash \circ A \leftrightarrow \neg (\circ (\neg A))$
$\diamond$ の定義: $\vdash \diamond A \leftrightarrow \neg ({\small \Box} (\neg A))$

推論規則: モーダスポネンス +

一般化: $\displaystyle \frac{\vdash A}{\vdash {\small \Box} A}$

それぞれの演算子の直観的な意味は,

$\circ A$ … 次の時刻で $A$ が成り立つ
${\small \Box} A$ … 常に $A$ が成り立つ
$\diamond A$ … いつか(未来のある時刻で) $A$ が成り立つ

である.

$\mathscr{L}$ は健全かつ完全である.

自作言語 nml の型システム

nml は私が1年半ほど前からちまちま作っている自作プログラミング言語で, 思いついた機能をとりあえず実装しては遊んでいる.

nml のコア言語は非 Turing 完全で, 合流性や正規化可能性(停止性)を持つ. ただ入出力や停止しない可能性のあるループ⁸を表現するために型システムに線形時相論理を組み込んでおり, コア言語での簡約と時刻を進める操作を分離している. これによって,

ある時刻における計算は純粋なまま保たれ, 必ず停止する.
非純粋な動作は全て時刻が進むときに行われる.

ようになっており,

全体として, 計算が線形に行われることが保証される.
GHC の RealWorld のようなコンパイラ・マジックが不要. 実際の計算順序は型が決定する.
時刻内の計算は非正格評価で行うことができる. 現行バージョンの nml は遅延評価だけでなく部分評価⁹も行う.

nml では $\circ A$ 型を Next[1] A, $\circ (\circ A)$ 型を Next[2] A, $\diamond A$ 型を Next[inf] A と表記する(つまり, 入れ子になった時相演算子を平らにして表記する).

全ての型は展開と一般化で自由に $\small \Box$ を付け外しできるので, 暗黙に ${\small \Box}$ が付いているとみなす.

$\circ A \rightarrow \diamond A$ と $\diamond (\diamond A) \rightarrow \diamond A$ より $\diamond (\circ A) \rightarrow \diamond A$ と $\circ (\diamond A) \rightarrow \diamond A$ が成立するため, Next[inf] より先の時刻の型は全て Next[inf] に飛ばすことができる.

また, $\circ ({\small \Box} A) \rightarrow \circ (\circ ({\small \Box} A))$ なので,

A <: Next[1] A <: Next[2] A <: ... <: Next[inf] A

という部分型関係を組み込んでいる. これによって, Next[inf] A 型を取る関数を Next[1] A 型の値に適用することができる.

そして, nml プログラムの実行は

eval :: Next[inf] a -> a
eval program = run[inf] program

として定義されている. つまり, ある n で Next[n] a という型が付いているプログラム(=線形なプログラム)しか実行できないことを型レベルで制約できている.

nml の構文

(@ @) で囲むと時刻1クォートできる. (@ 1 @) は Next[1] Nat 型.

<@ @> で囲むと無限時刻クォートできる. <@ 1 @> は Next[inf] Nat 型. なお Next[inf] 型は Finally 型として表示される. よって Finally Nat 型.

$\circ$ はモナドではないのだが, 利便性のために do-notation 的なものを入れている.

let-next[1] x = (@ 1 @) in
if x = 0 then
  true
else
  false

というコードは

let x = (@ 1 @) in
(@
  if (run[1] x) = 0 then
    true
  else
    false
@)

と等価で, 全体の型は Next[1] Bool になる. ただし, run[t] は処理系のみが内部で使う, 引数の時刻を t 進める関数¹⁰. なお, t=1 のとき [1] は省略できる.

同様に, $\diamond$ にも do-notation 的なものがある.

let-finally x = <@ 1 @> in x + 1

は

let x = <@ 1 @> in <@ (run[inf] x) + 1 @>

と等価で Finally Nat 型. ちなみに $\diamond$ はモナドになる.

ここで, 入力関数を

readNat :: Unit -> Next[1] Nat

と定義すれば,

let-next x = readNat () in
let-next y = readNat () in
let-next z = readNat () in
(x + y) * z

と書けて, 全体の型は Next[3] Nat になり, 実行時には3回入力が発生する.

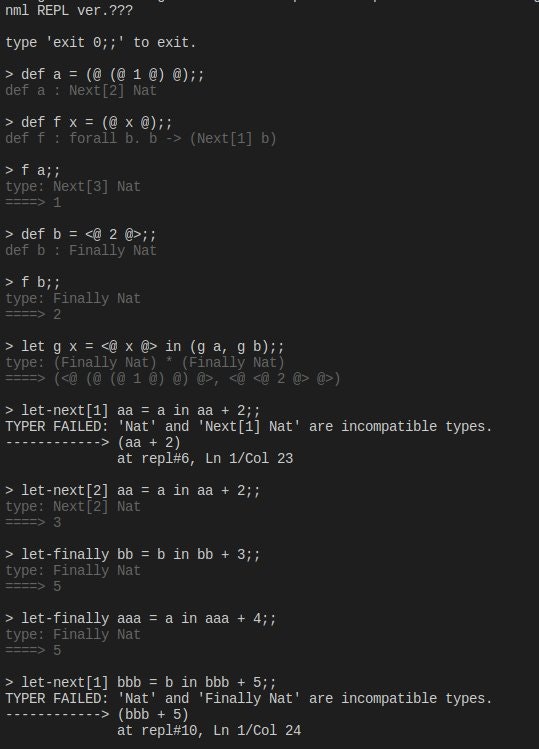
部分型はこんな感じに働く:

モジュールシステムは実装をかなりサボってて, まずモジュールレベル let と式レベル let がパーサ書くときに紛らわしくて前者のキーワードを def にした.

また, nml では帰納的データ型 (Inductive Datatypes) に対して帰納的関数を書くことができて, 要するに停止性が証明できる¹¹関数は時刻を進めずに計算できる.

停止性が証明された2分探索木はこう書ける.

inductive Bst a =
    Node of a * Bst a * Bst a
  | Leaf

module Bst = begin
  def insert x = 
    fixpoint f of
      Leaf -> Node (x, Leaf, Leaf)
    | Node (y, left, right) ->
      if x < y then
        Node (y, f left, right)
      else
        Node (y, left, f right)

  def contains x =
    fixpoint f of
      Leaf -> false
    | Node (y, left, right) ->
      if x < y then f left
      else if x = y then true
      else f right

  def height =
    fixpoint f of
      Leaf -> 0
    | Node (_, left, right) ->
      1 + max (f left) (f right)

  def itemsAtDepth depth tree =
    let f = 
      fixpoint f of
        Leaf -> fun _ -> []
      | Node (a, left, right) ->
        begin fun d ->
          if d = depth then
            [a]
          else
            List.append (f left (d+1)) (f right (d+1))
        end
    in f tree 0
end

今後

今後の予定はひとまず無限ループを $\diamond$ 型を付けて実装することである. あとは面白そうな機能をとりあえず入れてみる感じになるが, 今優先度が高いのは, 帰納的関数の停止性検査で扱えるものを増やすために sized types の研究をすることである. また, 形式化が済んでいる部分と実装が済んでいる部分のギャップがかなりあるのでそのうち一致させたい¹².

あと Finally はいくら足しても Finally なのでかなり強いことができるはずで, 並列計算も

parallel :: List (Finally a) -> Finally (List a)

としてうまく表現できそうなのでそれも試してみたい. 他にも色々できそうだ.

本当はもうちょっと色々書くつもりだったんですけど, 書いてるうちにこっちのほうが筋が良いのではとか色々思い浮かんできて, 結局あんまり書けませんでした. ごめんなさい.

予約投稿にしてあります. ↩
プログラミング言語(の設計・仕様)とプログラミング言語の実装を混同しないこと. この記事は前者を指して "プログラミング言語" という. ↩
私が勝手に言ってるだけで特にそういう用語があるわけではないです. ↩
どこからどういう順番で簡約しても結果が同じになる性質. これがあると最適化の多くがプログラム中の簡約できる部分を先に簡約するだけのことになる. ↩
厳密には State# RealWorld -> (# State# RealWorld, a #) ↩
もちろん, 本当に現実世界を操作できたりはしない ↩
Ben-Ari, Mordechai. (2012). Temporal Logic: A Deductive System. 10.1007/978-1-4471-4129-7_14. https://www.researchgate.net/publication/279391295_Temporal_Logic_A_Deductive_System ↩
未実装. $\diamond$ 時相演算子は導入してあるので型システム上は表現可能. 春休みあたりに入れる予定. ↩
λ抽象の内部なども簡約できる. ↩
これはコンパイラ・マジックではないか？と思われるかもしれないが, 本当はそうではない. 純粋なコードをいくらクォートしようが純粋なので, クォートした分まではその内部で run で時刻を進めても問題はなく, 本当はユーザも書けるべき. ただその検査を書くのがめんどくさそうなのでまだ入れていない. ↩
ここの話もしたかったけど書き出したらきりがない. 現状の型システムは Hindley-Milner + Inductive Datatypes + 線形時相型で, 停止性は引数が単調減少するかで判定するが, Coq のようにユーザが証明を書けるわけではないので自明なケースしか扱えない. それでも ackermann 関数くらいは書ける. そのうち Coinductive も入れる. ↩
モジュールシステムが鬼門か, と思っていたけど今回のアドベントカレンダーに素晴らしい記事があったので参考にさせていただきます. ↩