はじめに
本記事では、数ある畳み込み手法の中から、比較的よく用いられるものを改めて整理しました。特に、以下の観点に着目してまとめています。
- 簡単な計算方法
- パラメータ数
- PyTorch による実装例
なお、本記事では画像処理を対象とした2次元畳み込みを前提としています。また、畳み込みの詳細な処理内容については別の記事をご参照ください。
Standard Conv(標準畳み込み)
標準畳み込みは、CNN(畳み込みニューラルネットワーク)の基本演算です。小さな窓(カーネル)を画像(または特徴マップ)にスライドしながら乗算・加算を行い、重要な特徴を取り出します。
1. 処理の流れ
- カーネルの設置:例えば3×3サイズのフィルタを画像の左上に置く
- 要素ごとの乗算:カーネルの各重みと対応する画素値を掛け合わせる
- 合計(足し算):乗算結果を全て足し合わせる
- バイアス追加:さらに定数(バイアス)を足して1ピクセルの出力を得る
- スライド:右に指定ピクセル(ストライド)ずらし、同じ処理を繰り返す
- 全画素処理:画像全体に対してスライドし、出力マップを得る
参考:畳み込み層 (Convolution Layer)とその発展型
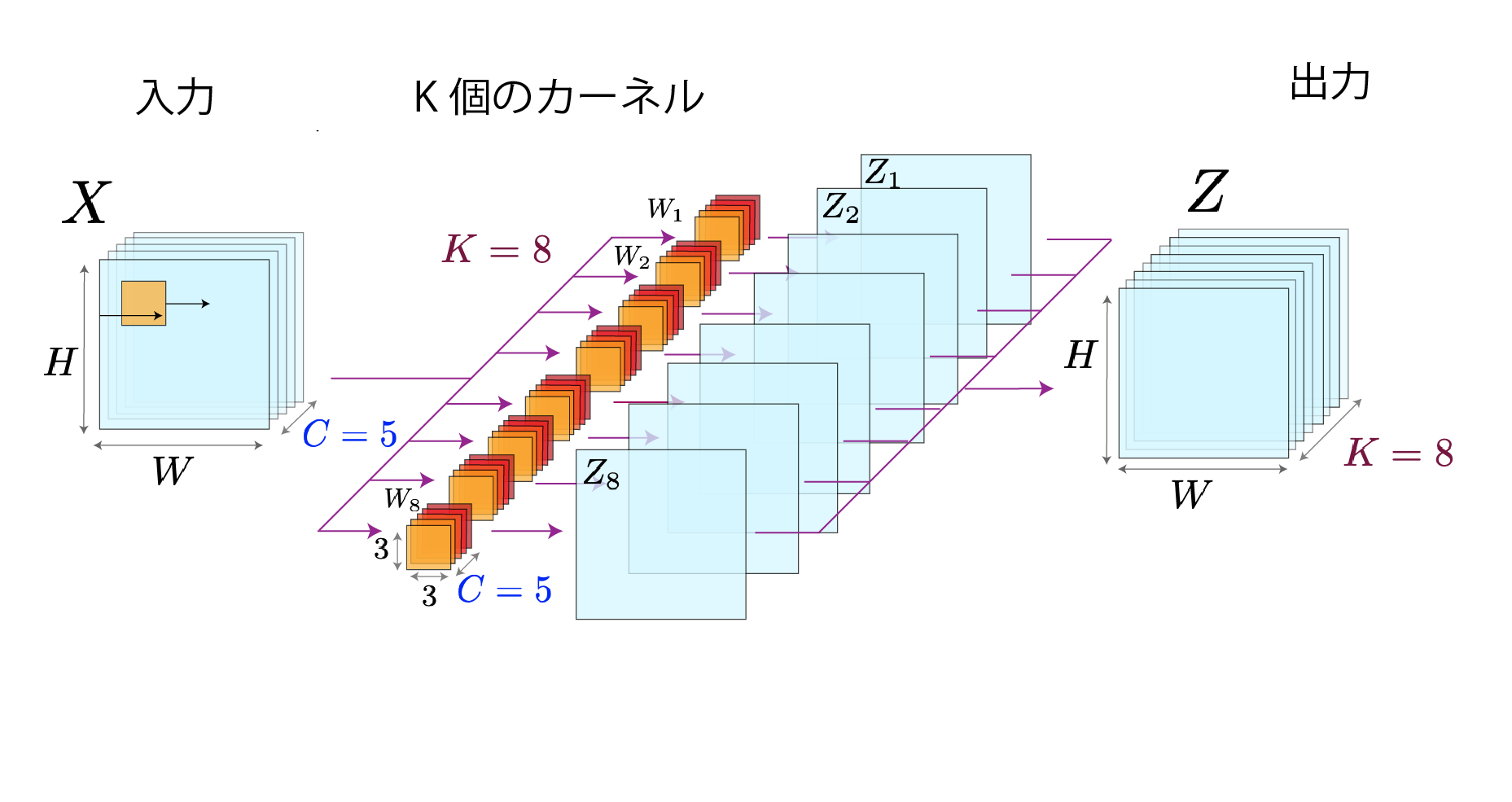
標準的な畳み込みは、1枚のカーネルを各入力チャネル上でスライドさせて得られるチャネルごとの特徴マップを合計し、その一連の演算を出力チャネル数(カーネル数)だけ繰り返す処理をします。
2. 数式による定義
出力マップの位置 $(i, j)$ のチャネル $k$ における値 $y_{i,j}^{(k)}$ は:
$$
y_{i,j}^{(k)} =
\sum_{c=1}^{C_{in}} \sum_{u=1}^{K_h} \sum_{v=1}^{K_w}
x_{i+u-1,,j+v-1}^{(c)} \times w_{u,v}^{(c,k)} + b^{(k)}
$$
- $C_{in}$:入力チャネル数
- $K_h, K_w$:カーネルの縦・横サイズ(例:$3×3$)
- $w_{u,v}^{(c,k)}$:入力チャネル $c$ → 出力チャネル $k$ の重み
- $b^{(k)}$:出力チャネル $k$ のバイアス
3. パラメータ数
1層あたりの学習パラメータ総数:
$$
\mathrm{Params} = C_{in} \times C_{out} \times K_h \times K_w + C_{out}
$$
- 最初の項:重み $C_{in} \times C_{out} \times K_h \times K_w$
- 後ろの $C_{out}$:バイアス数
4. PyTorch 実装例
conv = nn.Conv2d(
in_channels=64, # 入力チャネル数
out_channels=128, # 出力チャネル数
kernel_size=3, # カーネルサイズ3×3
stride=1, # ストライド1
padding=1, # パディング1→入力と同じ解像度
bias=True # バイアス有効
)
-
stride=1, padding=1:入力と同じサイズ -
stride=2, padding=1:解像度を半分にダウンサンプル
5. よく使われる場面
標準畳み込みは汎用的なフィルタ演算として、以下のタスクで主に使われます:
- 画像分類(例:ResNet, VGG)
- 物体検出(例:YOLO, Faster R-CNN)
- セグメンテーション(例:U-Net, FCN)
- 超解像/スタイル変換(例:SRGAN)
Pointwise Conv (1×1畳み込み, 点単位畳み込み)
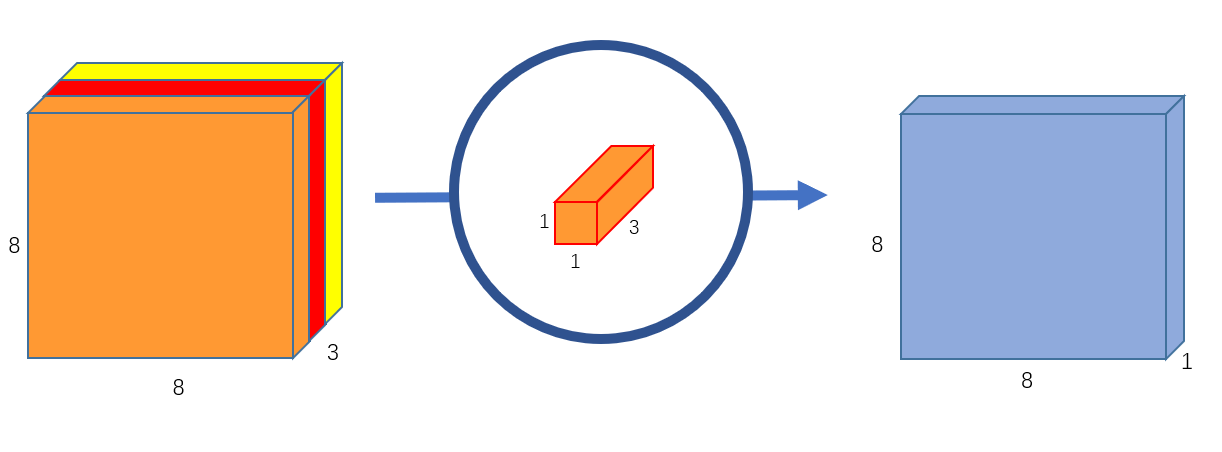
Pointwise Convは、1×1サイズのカーネルを使用してチャネル間の情報を統合・変換する手法です。空間方向の特徴抽出は行わず、各位置でのチャネル次元の線形結合のみを実行し、効率的にチャネル数を調整できます。
Standard Convとの違い:
Pointwise Convは、1×1サイズのカーネルで各画素のチャネル間だけを線形結合するため、標準的な畳み込みのような空間的特徴抽出は行いません。一方で、チャネル数の圧縮・拡張を効率的に行え、パラメータ数や計算量を大幅に削減できるため、モダンなCNNではボトルネック層やDepthwise Separable Convolutionにおけるチャネル変換に欠かせない軽量・高効率な演算です。
1. 処理の流れ
- カーネルの設置:1×1サイズのフィルタを各ピクセルに配置
- 要素ごとの乗算:フィルタの重みと対応チャネルの値を掛け合わせる
- 合計(足し算):乗算結果をチャネル間で足し合わせる
- バイアス追加:チャネルごとにバイアスを足して出力チャネル値を得る
図のように、1×1サイズのカーネルをチャネル方向にのみ適用し、出力チャネル数分用意することで、空間解像度を維持したままチャネル間の線形結合が可能になります。
2. 数式による定義
入力位置 $(i, j)$ における出力チャネル $k$ の値 $y_{i,j}^{(k)}$ は:
$$
y_{i,j}^{(k)}
= \sum_{c=1}^{C_{\mathrm{in}}}
x_{i,j}^{(c)} \times w^{(c,k)} + b^{(k)}
$$
- $C_{\mathrm{in}}$:入力チャネル数
- $w^{(c,k)}$:入力チャネル $c$ → 出力チャネル $k$ の重み
- $b^{(k)}$:出力チャネル $k$ のバイアス
3. パラメータ数
1×1畳み込みのパラメータ総数は次の通り:
$$
\mathrm{Params}
= C_{\mathrm{in}} \times C_{\mathrm{out}}+ C_{\mathrm{out}}
$$
- 最初の項:重みの数 $C_{\mathrm{in}} \times C_{\mathrm{out}}$
- 後ろの $C_{\mathrm{out}}$:バイアス数
標準的な $K_h \times K_w$ 畳み込みと比べると、1×1 畳み込みは
$$
\frac{Params_{1 \times 1}}{Params_{std}} = \frac{C_{in} C_{out} + C_{out}}{K_h K_w C_{in} C_{out} + C_{out}} \approx \frac{1}{K_h K_w}
$$
となり、パラメータ数も計算量も約 $1/({K_hK_w})$ 倍に削減されます。
例えば:
- $K_h = K_w = 3$ の場合 → 約 ${1}/{9}$
- $K_h = K_w = 5$ の場合 → 約 ${1}/{25}$
以上より、1×1畳み込みが非常に軽量なモジュールであることがわかります。
4. PyTorch 実装例
# 入力チャネル128 → 出力チャネル256 の1×1畳み込み
conv1x1 = nn.Conv2d(
in_channels=128,
out_channels=256,
kernel_size=1, # 1×1カーネル
stride=1, # ストライド1
padding=0, # 空間サイズを変化させない
bias=True # バイアス有効
)
5. よく使われる場面
- チャネル圧縮/拡張:Residual Bottleneck 内でチャネル数を調整
- 軽量モデル:Depthwise-Separable Conv と併用して計算量を削減(MobileNet など)
Depthwise Conv (深さ単位畳み込み)
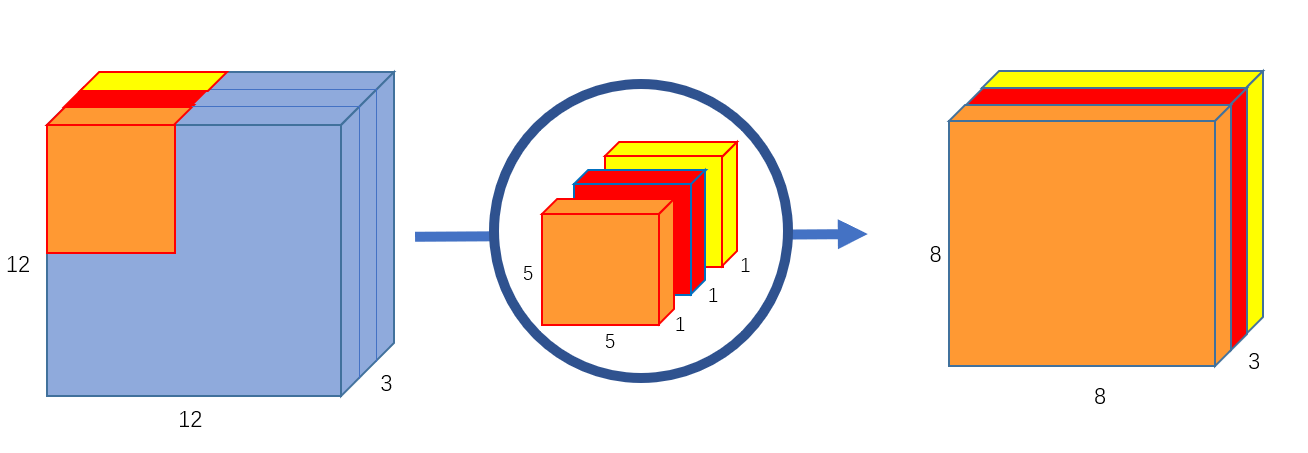
Depthwise Convは、各入力チャネルごとに独立したカーネルを適用し、空間方向のフィルタ処理をチャネル単位で行う手法です。チャネル間の混合はせず、演算量とパラメータ数を大幅に削減できます。
Standard Convとの違い:
Depthwise Convは各チャネルに対して独立した $K_h \times K_w$ カーネルを適用し、出力チャネル数は入力チャネル数と同じになります。一方、Standard Convは全チャネルを結合してフィルタを適用します。
1. 処理の流れ
-
チャネルごとに適用
各入力チャネルに対し、それぞれ $K_h \times K_w$のカーネルを配置 -
乗算→合計
カーネルと対応画素を乗算し、チャネル内で足し合わせ -
バイアス追加
各チャネルごとにバイアスを足して最終出力を得る -
全チャネル繰り返し
入力全チャネルを同様に処理して、出力マップを作成
標準的な畳み込みでは1枚のカーネルは入力チャネル全てに対して計算を行うのに対し、Depthwise Convは、図のように1枚の入力チャネルに対して1枚の独立したカーネルのみで計算を行うのが特徴です。
2. 数式による定義
入力位置 $(i, j)$ のチャネル (c) に対する出力値 $y_{i,j}^{(c)}$ は:
$$
y_{i,j}^{(c)}
= \sum_{u=1}^{K_h} \sum_{v=1}^{K_w}
x_{i+u-1,,j+v-1}^{(c)} \times w_{u,v}^{(c)}+ b^{(c)}
$$
- $w_{u,v}^{(c)}$:チャネル $c$ 用カーネルの重み
- $b^{(c)}$:チャネル $c$ のバイアス
3. パラメータ数
$$
\mathrm{Params}
= C_{\mathrm{in}} \times K_h \times K_w
+\ C_{\mathrm{in}}
$$
- 重み:$C_{\mathrm{in}} \times K_h \times K_w$
- バイアス:$C_{\mathrm{in}}$
標準的な $K_h \times K_w$ 畳み込みと比べると、Depthwise Conv のパラメータ削減割合は
$$
\frac{Params_{dw}}{Params_{std}}
= \frac{C_{in}(K_h K_w + 1)}{C_{out} \cdot C_{in} \cdot K_h K_w + C_{out}}
\approx \frac{1}{C_{out}}
$$
となり、パラメータ数も計算量も約 $1/C_{\mathrm{out}}$倍に削減されます。
例えば出力チャネル数 $C_{\mathrm{out}}=64$ の場合、計算コストは約 $1/64$ に削減されます。
以上より、Depthwise Conv は空間方向の特徴抽出を行う軽量モジュールであることが分かります。
4. PyTorch 実装例
# groups=in_channels でDepthwise Convを実現
depthwise = nn.Conv2d(
in_channels=64,
out_channels=64, # 出力チャネル数 = 入力チャネル数
kernel_size=3, # 3×3カーネル
stride=1,
padding=1,
groups=64, # チャネル独立処理
bias=True
)
pytrochではgroupsとout_channels引数をin_channlesと同じ値に設定することでDWConvを実装できます。
5. よく使われる場面
- モバイル/組み込み機器向け軽量化:演算量とメモリを削減しつつ畳み込みを実現
- 軽量モデル:Depthwise-Separable Conv と併用して計算量を削減(MobileNet など)
Depthwise-Separable Conv (深さ単位分離可能畳み込み)
Depthwise-Separable Convは、Depthwise ConvとPointwise Convを組み合わせた手法で、標準的な畳み込みを2段階に分離することで大幅な計算量削減を実現します。空間方向の特徴抽出とチャネル間の情報統合を分離して処理するのが特徴です。
Standard Convとの違い:
Standard Convが空間・チャネル両方向を同時に処理するのに対し、Depthwise-Separable Convは空間方向(Depthwise)とチャネル方向(Pointwise)を分離して順次処理します。
1. 処理の流れ
-
Depthwise Conv(空間フィルタリング)
各入力チャネルに対し、それぞれ独立した $ K_h×K_w $カーネルを適用 -
Pointwise Conv(チャネル統合)
1×1 カーネルで全チャネルの情報を統合し、出力チャネル数を調整
参考:深さ単位分離可能畳み込み (Depthwise Separable Convolution)
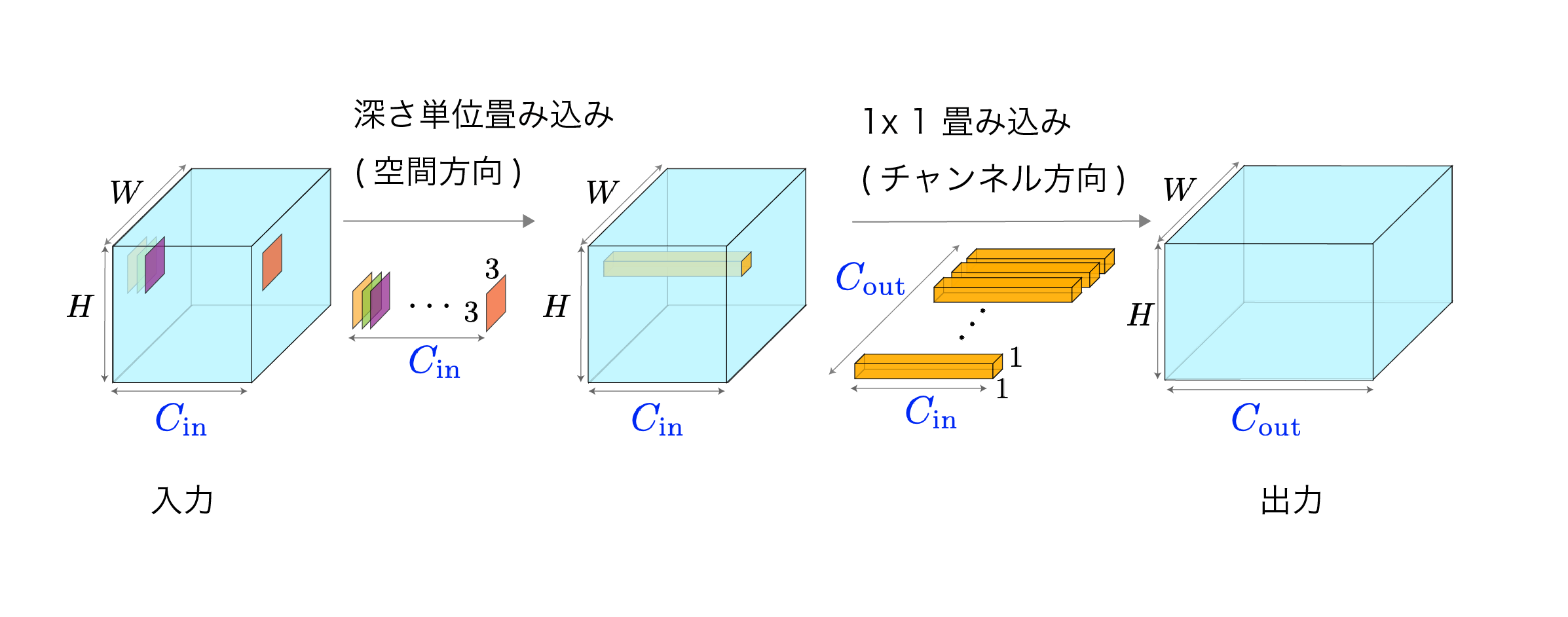
標準的な畳み込みが1つのステップで空間・チャネル両方向を処理するのに対し、Depthwise-Separable Convは図のように2段階に分けて処理することで効率化を図ります。
2. 数式による定義
Step 1: Depthwise Conv: 省略(前述の通り)
Step 2: Pointwise Conv 省略(前述の通り)
3.パラメータ数
$$
\mathrm{Params}
= C_{\mathrm{in}} \times K_h \times K_w + C_{\mathrm{in}}+ C_{\mathrm{in}} \times C_{\mathrm{out}} + C_{\mathrm{out}}
$$
- Depthwise部分:$C_{\mathrm{in}} \times K_h \times K_w + C_{\mathrm{in}}$
- Pointwise部分:$C_{\mathrm{in}} \times C_{\mathrm{out}} + C_{\mathrm{out}}$
標準的な畳み込みと比べると、パラメータ削減割合は:
$$
\frac{Params_{ds}}{Params_{std}}
= \frac{C_{in}(K_h K_w + 1) + C_{out}(C_{in} + 1)}{C_{out} \cdot C_{in} \cdot K_h K_w + C_{out}}
\approx \frac{1}{C_{out}} + \frac{1}{K_h K_w}
$$
例えば $3 \times 3$ カーネル($K_h = K_w = 3$)の場合、計算量は約 $1/8 \sim 1/9$ に削減されます。
4. Pytorch実装例
class DepthwiseSeparableConv(nn.Module):
def __init__(self, in_channels, out_channels, kernel_size=3, stride=1, padding=1):
super().__init__()
# Step 1: Depthwise Conv
self.depthwise = nn.Conv2d(
in_channels=in_channels,
out_channels=in_channels, # 出力チャネル数 = 入力チャネル数
kernel_size=kernel_size,
stride=stride,
padding=padding,
groups=in_channels, # チャネル独立処理
bias=True
)
# Step 2: Pointwise Conv
self.pointwise = nn.Conv2d(
in_channels=in_channels,
out_channels=out_channels,
kernel_size=1, # 1×1カーネル
stride=1,
padding=0,
bias=True
)
def forward(self, x):
x = self.depthwise(x) # 空間方向の特徴抽出
x = self.pointwise(x) # チャネル方向の情報統合
return x
# 使用例
ds_conv = DepthwiseSeparableConv(in_channels=64, out_channels=128, kernel_size=3)
5. よく使われる場面
- モバイル向け軽量化: MobileNet、MobileNetV2などの軽量アーキテクチャの基幹モジュール
- エッジコンピューティング: 限られた計算資源でのリアルタイム画像処理
Grouped Conv (グループ畳み込み)
Grouped Convは、入力チャネルを複数のグループに分割し、各グループ内で独立に畳み込み処理を行う手法です。チャネル間の接続を制限することで、パラメータ数と計算量を削減しながら、異なる特徴表現を並列に学習できます。
Standard Convとの違い:
Standard Convが全チャネル間で完全に接続されるのに対し、Grouped Convは指定されたグループ内でのみ接続を行い、グループ間での直接的な情報交換は行いません。
Depthwise Convとの関係:
Depthwise ConvはGrouped Convの特殊ケースです。グループ数 $G$ を入力チャネル数 $C_{\mathrm{in}}$ と等しくすると($G = C_{\mathrm{in}}$)、各チャネルが独立したグループとなり、これがDepthwise Convになります。
1. 処理の流れ
-
チャネル分割
入力チャネルを $G$ 個のグループに均等分割(各グループ $C_{\mathrm{in}}/G$ チャネル) -
グループ内畳み込み
各グループ内で独立した畳み込み処理を並列実行
参考:グループ化畳み込み(Grouped Convolution)
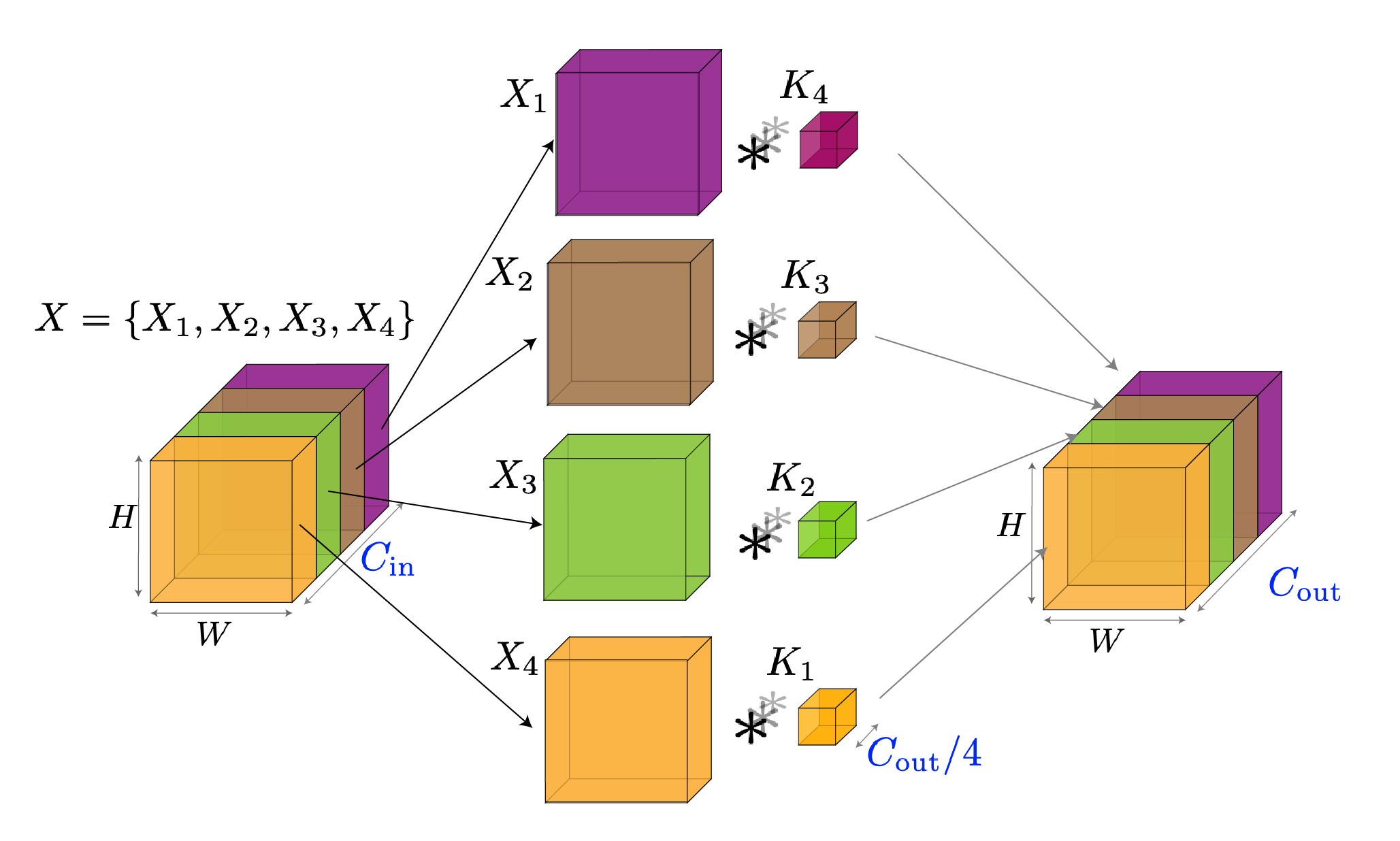
標準的な畳み込みが全チャネル間で密に接続されるのに対し、Grouped Convは図のようにグループ内でのみ接続することで計算効率を向上させます。
2. 数式による定義
グループ $g$ における出力位置 $(i, j)$ のチャネル $d$ に対する出力値 $y_{i,j}^{(g,d)}$ は:
$$
y_{i,j}^{(g,d)} = \sum_{c=1}^{C_{\mathrm{in}}/G} \sum_{u=1}^{K_h} \sum_{v=1}^{K_w}
x_{i+u-1,,j+v-1}^{(g,c)} \times w_{u,v}^{(g,c,d)} + b^{(g,d)}
$$
- $G$:グループ数
- $x_{i,j}^{(g,c)}$:グループ $g$ の入力チャネル $c$ の値
- $w_{u,v}^{(g,c,d)}$:グループ $g$ 内のカーネル重み
- $b^{(g,d)}$:グループ $g$ の出力チャネル $d$ のバイアス
Depthwise Convの場合($G = C_{\mathrm{in}}$):
各グループが1チャネルのみを含むため、上式は前述のDepthwise Convの式と一致します。
3. パラメータ数
$$
\mathrm{Params}
= G \times \frac{C_{\mathrm{in}}}{G} \times \frac{C_{\mathrm{out}}}{G} \times K_h \times K_w + C_{\mathrm{out}}
= \frac{C_{\mathrm{in}} \times C_{\mathrm{out}} \times K_h \times K_w}{G} + C_{\mathrm{out}}
$$
- 重み:$\frac{C_{\mathrm{in}} \times C_{\mathrm{out}} \times K_h \times K_w}{G}$
- バイアス:$C_{\mathrm{out}}$
標準的な畳み込みと比べると、パラメータ削減割合は:
$$
\frac{Params_{grouped}}{Params_{std}}
= \frac{\frac{C_{in} \times C_{out} \times K_h \times K_w}{G} + C_{out}}{C_{in} \times C_{out} \times K_h \times K_w + C_{out}}
\approx \frac{1}{G}
$$
Depthwise Convの場合($G = C_{\mathrm{in}}$, $C_{\mathrm{out}} = C_{\mathrm{in}}$):
この式は前述のDepthwise Convのパラメータ削減割合 $\approx 1/C_{\mathrm{out}}$ と一致します。
例えば $G=8$ の場合、パラメータ数と計算量は約 $1/8$ に削減されます。
4. PyTorch実装例
grouped_conv = nn.Conv2d(
in_channels=64,
out_channels=128,
kernel_size=3,
stride=1,
padding=1,
groups=8, # 8グループに分割
bias=True
)
5. よく使われる場面
- モバイル向け軽量化: MobileNet、MobileNetV2などの軽量アーキテクチャの基幹モジュール
- エッジコンピューティング: 限られた計算資源でのリアルタイム画像処理
Dilated/Atrous Conv (拡張畳み込み)
Dilated Conv(Atrous Convとも呼ばれる)は、カーネル要素間に空白(dilation)を挿入して受容野を拡張する畳み込み手法です。パラメータ数や計算量を増やすことなく、より広い範囲の特徴を捉えることができ、特にセマンティックセグメンテーションや画像解析で威力を発揮します。
Standard Convとの違い:
Standard Convが連続したピクセルに対してカーネルを適用するのに対し、Dilated Convは指定した間隔(dilation rate)でピクセルをサンプリングしてカーネルを適用します
1. 処理の流れ
-
カーネル拡張
通常の 3×3カーネルの要素間に空白を挿入。dilation rate r=2 の場合、カーネル要素間に1つずつ空白が入り、実際にカバーする範囲は5×5になる -
間隔サンプリング
入力画像からrピクセルおきに値を取得。r=2なら1ピクセル飛ばしで値を取得してカーネルと掛け算
参考:膨張畳み込み層 (Dilated Convolution)
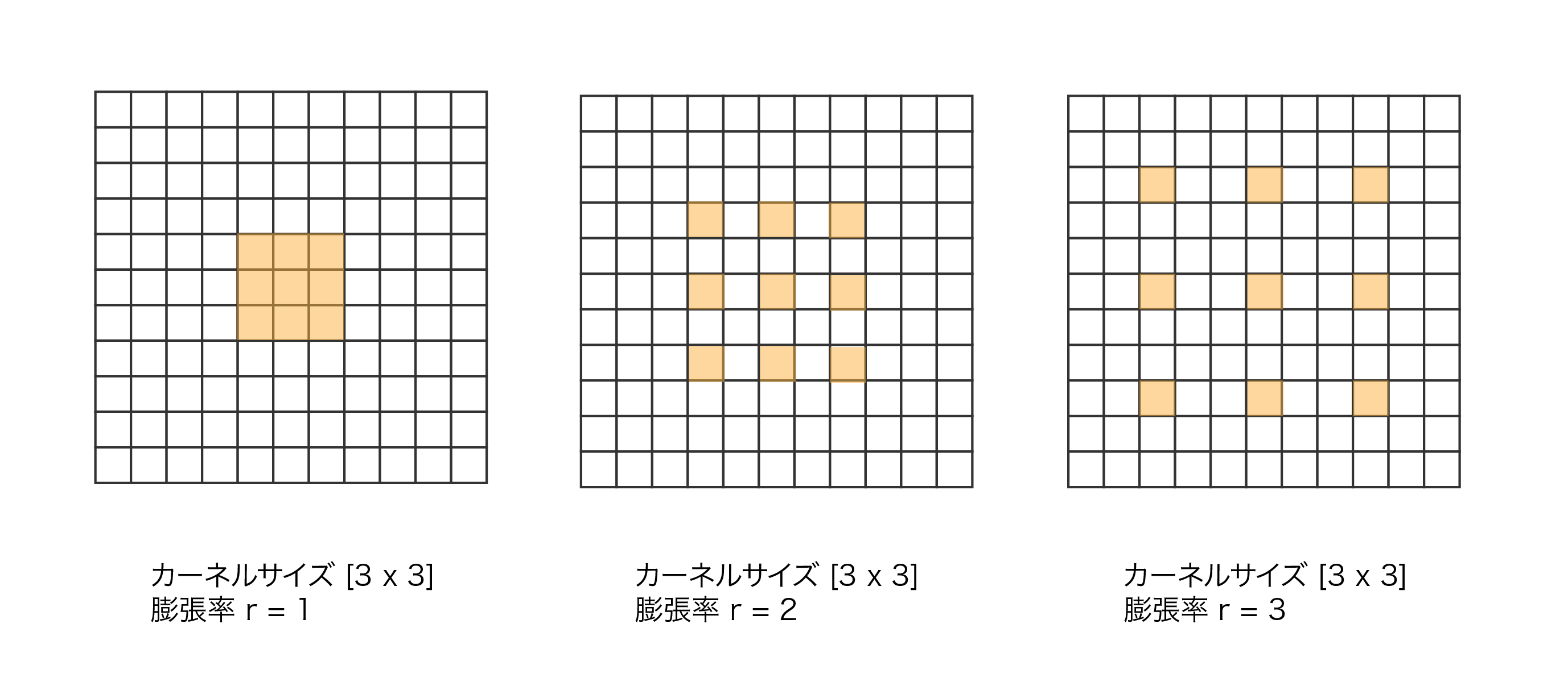
標準的な畳み込みが隣接ピクセルのみを使用するのに対し、Dilated Convは図のように間隔を空けてサンプリングすることで広範囲の特徴(受容野)を捉えます
2. 数式による定義
dilation rate $r$ を持つ Dilated Conv の出力位置 $(i, j)$ のチャネル $d$ に対する出力値 $y_{i,j}^{(d)}$ は:
$$
y_{i,j}^{(d)} = \sum_{c=1}^{C_{\mathrm{in}}} \sum_{u=1}^{K_h} \sum_{v=1}^{K_w}
x_{i+r(u-1),,j+r(v-1)}^{(c)} \times w_{u,v}^{(c,d)} + b^{(d)}
$$
- $r$:dilation rate(拡張率)
- $x_{i+r(u-1),j+r(v-1)}^{(c)}$:$r$ 間隔でサンプリングされた入力値
- $w_{u,v}^{(c,d)}$:カーネル重み
- $b^{(d)}$:バイアス
実効受容野サイズ:
$K_h \times K_w$ カーネルで dilation rate $r$ の場合:
$$
\text{Effective kernel size} = (K_h - 1) \times r + 1
$$
具体例:
- 通常の $3 \times 3$ カーネル:隣接する $3 \times 3 = 9$ ピクセルを使用
- dilation rate $r=2$ の場合:$5 \times 5$ の範囲から9ピクセルを飛び飛びで使用
- dilation rate $r=3$ の場合:$7 \times 7$ の範囲から9ピクセルを飛び飛びで使用
3. パラメータ数
dilation rateは計算方法を変えるだけで、カーネルサイズ自体は変わりません。そのため、パラメータ数は通常の畳み込みと全く同じです。
4. Pytorch実装例
dilated_conv = nn.Conv2d(
in_channels=64,
out_channels=128,
kernel_size=3,
stride=1,
padding=2, # dilation=2の場合、padding=2で同じサイズを維持
dilation=2, # dilation rate = 2
bias=True
)
5. よく使われる場面
- 画像の高解像度処理 :ダウンサンプリングなしで広い受容野を確保
- セマンティックセグメンテーション、物体検出:異なるスケールの物体や領域を広い受容野で効率的に検出
Deformable Conv (変形畳み込み)
Deformable Convは、従来の固定的な格子状サンプリング(3×3などの決められた範囲内)を学習可能なオフセットで変形させる畳み込み手法です。物体の形状や変形に柔軟に対応でき、不規則な形状やスケールの変化に強い特徴抽出を実現します。
Standard Convとの違い:
Standard Convが規則的な格子パターンで入力をサンプリングするのに対し、Deformable Convは各サンプリング位置に学習可能なオフセットを追加し、物体の形状に応じて動的にサンプリングパターンを調整します。
Dilated Convとの関係:
Dilated Convが固定的な間隔でサンプリングするのに対し、Deformable Convは学習によって最適なサンプリング位置を動的に決定する点で大きく異なります。
1. 処理の流れ
-
オフセット学習
入力特徴マップから各サンプリング位置のオフセット($\Delta x, \Delta y$)を学習 -
動的サンプリング
学習されたオフセットを基準位置に加算して、実際のサンプリング位置を決定
参考:Deformable Convolutional Networks
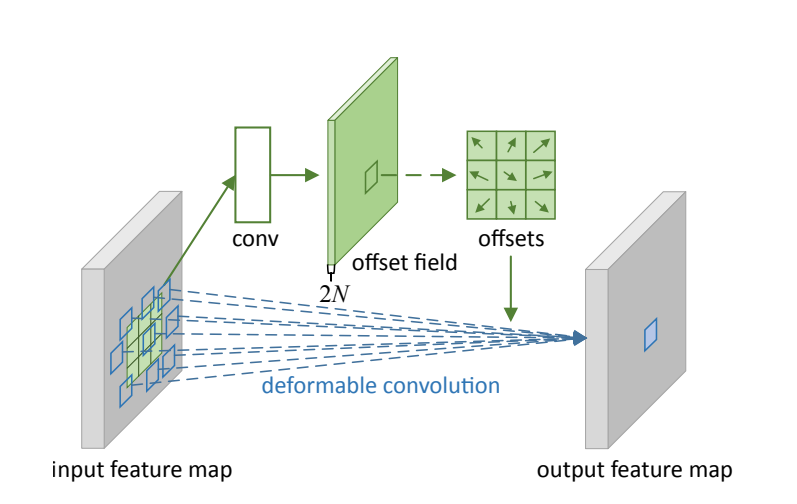
標準的な畳み込みが規則的な格子でサンプリングするのに対し、Deformable Convは図のように物体の形状に応じてサンプリング位置を動的に調整します。
2. 数式による定義
Deformable Conv の出力位置 $(i, j)$ のチャネル $d$ に対する出力値 $y_{i,j}^{(d)}$ は:
$$
y_{i,j}^{(d)} = \sum_{c=1}^{C_{\mathrm{in}}} \sum_{u=1}^{K_h} \sum_{v=1}^{K_w}
x_{i+u+\Delta u_{i,j},,j+v+\Delta v_{i,j}}^{(c)} \times w_{u,v}^{(c,d)} + b^{(d)}
$$
- $\Delta u_{i,j}, \Delta v_{i,j}$:位置 $(i,j)$ での学習されたオフセット
- $x_{i+u+\Delta u_{i,j},j+v+\Delta v_{i,j}}^{(c)}$:オフセット適用後の入力値(双線形補間)
- $w_{u,v}^{(c,d)}$:通常のカーネル重み
- $b^{(d)}$:バイアス
オフセット学習:
オフセットは別の畳み込み層で学習:
$$
{\Delta u_{i,j}, \Delta v_{i,j}} = \text{Conv}_{\text{offset}}(x)
$$
3. パラメータ数
$$
\mathrm{Params}
= (C_{\mathrm{in}} \times C_{\mathrm{out}} \times K_h \times K_w + C_{\mathrm{out}})+ (C_{\mathrm{in}} \times 2K_h K_w \times K_h \times K_w)
$$
- メイン畳み込み:$C_{\mathrm{in}} \times C_{\mathrm{out}} \times K_h \times K_w + C_{\mathrm{out}}$
- オフセット学習:$C_{\mathrm{in}} \times 2K_h K_w \times K_h \times K_w$(x,y方向で2倍)
標準的な畳み込みと比べると:
$$
\frac{Params_{deformable}}{Params_{std}} = 1 + \frac{2K_h K_w \times K_h \times K_w}{C_{\mathrm{out}} \times K_h \times K_w} \approx 1 + \frac{2K_h K_w}{C_{\mathrm{out}}}
$$
例えば $3 \times 3$ カーネル、$C_{\mathrm{out}}=64$ の場合、パラメータ数は約 1.28倍 に増加します。
4. Pytorch実装例
import torch
import torch.nn as nn
from torchvision.ops import deform_conv2d
class DeformableConv2d(nn.Module):
def __init__(self, in_channels, out_channels, kernel_size=3, stride=1, padding=1):
super().__init__()
self.kernel_size = kernel_size
# オフセット学習用の畳み込み層
self.offset_conv = nn.Conv2d(
in_channels,
2 * kernel_size * kernel_size, # x,y方向のオフセットで2倍
kernel_size=kernel_size,
stride=stride,
padding=padding,
bias=True
)
# メインの畳み込みの重み
self.weight = nn.Parameter(
torch.randn(out_channels, in_channels, kernel_size, kernel_size)
)
self.bias = nn.Parameter(torch.randn(out_channels))
def forward(self, x):
# オフセットを学習
offset = self.offset_conv(x)
# deform_conv2d関数を使用
return deform_conv2d(
input=x,
offset=offset,
weight=self.weight,
bias=self.bias
)
deform_conv = DeformableConv2d(in_channels=64, out_channels=128, kernel_size=3)
x = torch.randn(1, 64, 32, 32)
output = deform_conv(x)
5. よく使われる場面
- 物体検出: 不規則な形状の物体や回転・変形した物体の検出精度向上
- セマンティックセグメンテーション: 複雑な境界線や非規則形状の領域分割
Transposed Conv (転置畳み込み)
Transposed Convは、畳み込みの逆処理を行い、入力より大きなサイズの特徴マップを生成する手法です。「逆畳み込み」や「Deconvolution」とも呼ばれます。
Standard Convとの違い:
Standard Convが入力を小さくするのに対し、Transposed Convは入力を大きくします。畳み込み行列の転置を使用することで、ダウンサンプリングの逆操作(アップサンプリング)を実現します。
1. 処理の流れ
-
入力パディング
入力の各ピクセル間にゼロを挿入して、実効的なサイズを拡大 -
通常の畳み込み
パディングされた入力に対して標準的な畳み込みを適用
参考:What Are Transposed Convolutions?
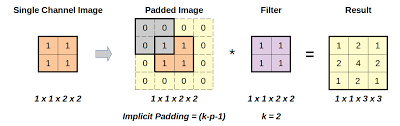
標準的な畳み込みが特徴マップを縮小するのに対し、Transposed Convは図のように特徴マップを拡大します。
2. 数式による定義
Transposed Conv の出力位置 $(i, j)$ のチャネル $d$ に対する出力値 $y_{i,j}^{(d)}$ は:
$$
y_{i,j}^{(d)} = \sum_{c=1}^{C_{\mathrm{in}}} \sum_{u=1}^{K_h} \sum_{v=1}^{K_w}
x_{\lfloor i/s \rfloor + u - p, \lfloor j/s \rfloor + v - p}^{(c)} \times w_{u,v}^{(c,d)} + b^{(d)}
$$
- $s$:stride
- $p$:padding
- $\lfloor \cdot \rfloor$:床関数
- $w_{u,v}^{(c,d)}$:カーネル重み
- $b^{(d)}$:バイアス
出力サイズの計算:
$$
H_{\mathrm{out}} = (H_{\mathrm{in}} - 1) \times \text{stride} - 2 \times \text{padding} + K_h
$$
$$
W_{\mathrm{out}} = (W_{\mathrm{in}} - 1) \times \text{stride} - 2 \times \text{padding} + K_w
$$
3. パラメータ数
Transposed Convのパラメータ数は通常の畳み込みと全く同じです。
4. PyTorch実装例
transposed_conv = nn.ConvTranspose2d(
in_channels=64,
out_channels=32,
kernel_size=4,
stride=2,
padding=1
)
5. よく使われる場面
- セマンティックセグメンテーション: U-Netなどでエンコーダで縮小した特徴マップを元のサイズに復元
- 超解像: 低解像度画像から高解像度画像への変換
おわりに
最近は Attention 機構をはじめ、多くの新しい手法が次々と登場していますが、その根底には畳み込みの「局所的受容野」や「重み共有」といった考え方が息づいているように思います。ですので、いま一度畳み込みの仕組みや派生手法を振り返っておくことで、モデル設計のヒントが得られるかもしれません。
本記事では標準畳み込みや Depthwise/Pointwise、転置畳み込みを紹介しましたが、GhostConvなど、まだまだ面白いバリエーションがたくさんあります。興味がある方は、これらを組み合わせた CNN 構造にもぜひ触れてみてください。