はじめに
このシリーズは、とある**算数教具「ジャマイカ」**について、
以下の目的を達成するべく奮闘する記録です。
✔︎ 1. 「ジャマイカ」のゲームを画像表示などを用いたプログラムで動かせるようになる。
▶︎ 2. 「ジャマイカ」におけるサイコロの任意の組み合わせについて、解の存在とその内容を探索・提示するプログラムを作る。
前回までのおさらい
前回までは、以下の内容を扱いました。
§1. 「ジャマイカ」を再現する
Task.001 「サイコロの出目」を画像で表示する
Task.002 「ランダムな数字に合わせてサイコロ出目画像を表示する」
Task.003 「サイコロ出目画像表示のための関数を作る」
これにより、
- サイコロをランダムに振る
- 振った結果に対応するサイコロの出目画像を並べて表示する
というジャマイカの基本動作を、数行のコードで実行できるようになりました。
_____【 参考記事 】_____
1 Recollection|算数教具「ジャマイカ」を再現しよう❗️の前々回記事(vol.01)
2 Recollection|算数教具「ジャマイカ」を再現しよう❗️の前回記事(vol.02)
### function trial START ###
libimports()
figPlace = figplace()
jmcDice = jmc_diceroll(printOption=True)
jmc_display(figPlace, jmcDice, sizeRatio=1.4)
### function trial END ###
> Drive already mounted at /content/drive; to attempt to forcibly remount, call drive.mount("/content/drive", force_remount=True).
> ジャマイカのダイスロール結果: [ 1 5 6 5 5 30 2]
§2. 「ジャマイカ」の解を探索する
■ ジャマイカでは白サイコロの数字をそれぞれ1回ずつ用いて、四則演算(加減乗除)を行い、黒サイコロの和を作り上げることが目的です。
■ 白サイコロの数字はどの順番で四則演算しても構いません。
例) 白サイコロ: 2, 2, 3, 3, 4 黒サイコロ: 40, 5 の場合
[1] 白サイコロを1回ずつ → 2*2*3*4 - 3 = 48 - 3 = 45
[2] 黒サイコロの和 → 40 + 5 = 45
と計算できるので、この四則演算の組は解となる。
Task.004 「ジャマイカルールに基づく四則演算関数を準備する」
■ 引き算や割り算で不可能な計算結果は、それ以降続かないようにしなければなりません。
例) 白サイコロ: 2, 2, 4, 5, 6 黒サイコロ: 40, 5 の場合
引き算: 2 - 6 = -4
割り算: 6 / 4 = 3/2
については、途中計算で用いることはできない。
※既約分数も許すルールがあります。
■ 以上のことから、次の四則演算の関数を作ります。
2数の和を計算する関数: add()
2数の差を計算する関数: substract() ※小さい方から大きい方を引いた結果はnanとする
2数の積を計算する関数: multiply()
2数の商を計算する関数: divide() ※結果が整数でない場合について、よしとするかどうかのオプションが必要
_____【 参考記事 】_____
3 Task004|【NANって何だ?】意味と用法
➡︎ 出力不能を表すために、np.nanを使えば良さそうであることに気づいた。
(後に結果判定する際に、意図しない外れ値がなくなることを期待している。)
def add(var1, var2):
return var1 + var2
def substract(var1, var2):
if var1 >= var2: #第1引数が第2引数以上であれば、引き算を実行する
return var1 - var2
else: #第1引数が第2引数より小さければ、計算をそれ以降進行しないようにnanを出力する
return np.nan
def multiply(var1, var2):
return var1 * var2
def divide(var1, var2, fracOption): #第3引数 fracOption は Trueのときに限り既約分数を許可するオプション
if var2 == 0: #0で割る場合は、計算をそれ以降進行しないようにnanを出力する
return np.nan
elif isinstance(var1, int) and isinstance(var1, int): #2数がどちらも整数のとき
if not fracOption == True: #分数を許可しない場合
if var1 >= var2 and var1 % var2 ==0: #さらに1番目の数が2番目以上であり、割り切れる場合は、商を出力する
return var1 // var2
else: #1番目の数が2番目より小さいか、割り切れない場合は、計算をそれ以降進行しないようにnanを出力する
return np.nan
else: #分数を許可する場合は、そのまま割り算を実行する
return var1 / var2
else: #2数のいずれかが整数でないとき
if not fracOption ==True: #分数を許可しない場合は、計算をそれ以降進行しないようにnanを出力する
return np.nan
else: #分数を許可する場合は、そのまま割り算を実行する
return var1 / var2
### function trial START ###
# substractの計算結果をnanで出すかどうか?
print('___substractのチェック___')
for num in range(8):
print('6-',num,' = ',substract(6,num))
# divideの計算結果をfracOption=Trueでチェック
print('___divideのチェック1: fracOption=True & varA is int___')
for num in range(8):
print('6/',num,' = ',divide(6,num,fracOption=True))
# divideの計算結果をfracOption=Falseでチェック
print('___divideのチェック2: fracOption=False & varA is int___')
for num in range(8):
print('6/',num,' = ',divide(6,num,fracOption=False))
# divideの計算結果をfracOption=True & 割られる数がfloatでチェック
print('___divideのチェック3: fracOption=True & varA is float___')
for num in range(8):
print('6.5/',num,' = ',divide(6.5,num,fracOption=True))
# divideの計算結果をfracOption=False & 割られる数がfloatでチェック
print('___divideのチェック4: fracOption=False & varA is float___')
for num in range(8):
print('6.5/',num,' = ',divide(6.5,num,fracOption=False))
### function trial END ###
___substractのチェック___
6- 0 = 6
6- 1 = 5
6- 2 = 4
6- 3 = 3
6- 4 = 2
6- 5 = 1
6- 6 = 0
6- 7 = nan
___divideのチェック1: fracOption=True___
6/ 0 = nan
6/ 1 = 6.0
6/ 2 = 3.0
6/ 3 = 2.0
6/ 4 = 1.5
6/ 5 = 1.2
6/ 6 = 1.0
6/ 7 = 0.8571428571428571
___divideのチェック2: fracOption=False___
6/ 0 = nan
6/ 1 = 6
6/ 2 = 3
6/ 3 = 2
6/ 4 = nan
6/ 5 = nan
6/ 6 = 1
6/ 7 = nan
___divideのチェック3: fracOption=True & varA is float___
6.5/ 0 = nan
6.5/ 1 = 6.5
6.5/ 2 = 3.25
6.5/ 3 = 2.1666666666666665
6.5/ 4 = 1.625
6.5/ 5 = 1.3
6.5/ 6 = 1.0833333333333333
6.5/ 7 = 0.9285714285714286
___divideのチェック4: fracOption=False & varA is float___
6.5/ 0 = nan
6.5/ 1 = nan
6.5/ 2 = nan
6.5/ 3 = nan
6.5/ 4 = nan
6.5/ 5 = nan
6.5/ 6 = nan
6.5/ 7 = nan
Task.005 「ジャマイカの解を探索するための関数を考える」
■ 白サイコロを用いて、ジャマイカで解候補となる計算を進める関数として、次の発想が考えられます。
[手順1] 白サイコロ5個の出目、つまり5個の整数値(1以上6以下)のうち、任意の2個を選んで並べ(5P2=20通りの組み合わせ)、四則演算(加減乗除で4種類)を行う。
[手順2] 上記[1]で生じた数1個と残りの3個の整数値(1以上6以下)のうち、任意の2個を選んで並べ(4P2=12通りの組み合わせ)、四則演算(加減乗除で4種類)を行う。
[手順3] 上記[1][2]と同様の流れで、1個の数字を出力するまで続ける。
■ 上記の関数は次のような入力の条件に応じて出力を変化させなければならないでしょう。
(1) 入力される出目や計算結果のセット(np.array形式)
(2) (1)の内包値の個数(=配列の長さ)がもし1なら計算をやめて、合致判定を行う
(3) 分数を許可するか否か(fracOption == True or False)
■ また、四則演算をどの数にどの順で適用したのかどうか、記録を出力する必要がありますから、次のような出力も残していかなければならないでしょう。
(4) 2数を計算した四則演算について「(_varA_ _演算記号_ _varB_)」 を記録する
例) 2 * 5 の場合は、「(2 * 5)」を記録する
■ 以上を考えて、まずは次の関数を定義していきます。
■ 計算要素を演算可能な数値として格納する calcDice と、それを文字列化した calcDNames を出力します。
[関数1] transForClac()
___入力:サイコロ7個の結果を格納した配列 jmcDice
___出力:白サイコロ5個と黒サイコロの2個の和を格納した配列 calcDice
[関数2] makeCalcName()
___入力:白サイコロ5個と黒サイコロの2個の和を格納した配列 calcDice
___出力:数字を文字列化した(任意の長さの文字列に更新できる型の)配列 calcDNames
# [関数1] transForClac()
# ___入力:サイコロ7個の結果を格納した配列 jmcDice
# ___出力:白サイコロ5個と黒サイコロの2個の和を格納した配列 calcDice
###################################################
def transForCalc(jmcDice, printOption):
calcDice = jmcDice.astype(np.float64) #あとで計算要素を更新する際に、np.nan(float64形式)で上書きできるように、最初からfloat64の配列で再定義した calcDice を作る。
calcDice[5] = calcDice[5] + calcDice[6] #黒サイコロの値の和を計算して、index=5(つまり6番目)のサイコロの値に更新する
calcDice = np.delete(calcDice, 6) #不要になった、index=6(つまり7番目)のサイコロの値を削除する
if printOption == True:
print('計算要素の一覧: ', calcDice)
return calcDice
# [関数2] makeCalcName()
# ___入力:白サイコロ5個と黒サイコロの2個の和を格納した配列 calcDice
# ___出力:数字を文字列化した(任意の長さの文字列に更新できる型の)配列 calcDNames
###################################################
def makeCalcName(calcDice, printOption):
calcDNames = np.empty(calcDice.shape[0],dtype=object) #長さの異なる文字列を格納できるようにobject形式のnp.arrayを定義する(長さはcalcDiceの配列の長さと同じ)
for i in range(calcDNames.shape[0]):
calcDNames[i] = str(int(calcDice[i])) #文字化した calcDice の各要素を順次格納していく
if printOption == True:
print('文字化配列の一覧: ', calcDNames)
return calcDNames
### fanction trial START ###
jmcDice = jmc_diceroll(printOption=True)
calcDice = transForCalc(jmcDice, printOption=True)
calcDNames = makeCalcName(calcDice, printOption=True)
### fanction trial END ###
> ジャマイカのダイスロール結果: [ 2 3 1 4 4 50 5]
> 計算要素の一覧: [ 2. 3. 1. 4. 4. 55.]
> 文字化配列の一覧: ['2' '3' '1' '4' '4' '55']
_________________________________________
■ 計算要素のみの配列 calcDice と、それを文字列化した calcDNames を作ることができました。
■ 今度は、この中で好きな2数を選択し、四則演算のうちの1つを実践することが必要になります。
■ そこで、どの四則演算を行うかを指定する arithOpeNo を入力として、選んだ2数を四則演算するような、以下の関数を定義していきます。
[関数3] arithOperator()
___入力1:演算したい2数のうちの1番目 var1
___入力2:演算したい2数のうちの2番目 var2
___入力3:四則演算のうち何を使うかについて、指定する番号 arithOpeNo
___入力4:分数を許可するかどうかの選択オプション fracOption
___出力:2数の四則演算の結果
[関数4] arithMarker()
___入力:四則演算のうち何を使うかについて、指定する番号 arithOpeNo
___出力:2数を計算した演算記録に使うマーク
# [関数3] arithOperator()
# ___入力1:演算したい2数のうちの1番目 var1
# ___入力2:演算したい2数のうちの2番目 var2
# ___入力3:四則演算のうち何を使うかについて、指定する番号 arithOpeNo
# ___入力4:分数を許可するかどうかの選択オプション fracOption
# ___出力:2数の四則演算の結果
###################################################
def arithOperator(var1, var2, arithOpeNo, fracOption):
if arithOpeNo == 0: #arithOpeNoで0を指定すると足し算
return add(var1, var2)
elif arithOpeNo == 1: #arithOpeNoで1を指定すると引き算
return substract(var1, var2)
elif arithOpeNo == 2: #arithOpeNoで2を指定すると掛け算
return multiply(var1, var2)
elif arithOpeNo == 3: #arithOpeNoで3を指定すると割り算
return divide(var1, var2, fracOption)
else: #arithOpeNoが0,1,2,3ではない場合は、それ以降演算結果が出ないようにnp.nanを出力する
return np.nan
# [関数4] arithMarker()
# ___入力:四則演算のうち何を使うかについて、指定する番号 arithOpeNo
# ___出力:2数を計算した演算記録に使うマーク
###################################################
def arithMarker(arithOpeNo):
if arithOpeNo == 0: #arithOpeNoで0を指定すると足し算
return ' + '
elif arithOpeNo == 1: #arithOpeNoで1を指定すると引き算
return ' - '
elif arithOpeNo == 2: #arithOpeNoで2を指定すると掛け算
return ' * '
elif arithOpeNo == 3: #arithOpeNoで3を指定すると割り算
return ' / '
else: #arithOpeNoが0,1,2,3ではない場合は、計算できなかったとして|???|を表示する
return ' |???| '
### fanction trial START ###
var1 = 19
var2 = 4
print('___四則演算の結果___ for ', var1, ' & ', var2)
for i in range(6):
print(arithOperator(var1, var2, arithOpeNo=i, fracOption=True))
print('___四則演算のマーク___')
for i in range(6):
print(arithMarker(arithOpeNo=i))
### fanction trial END ###
___四則演算の結果___ for 19 & 4
23
15
76
4.75
nan
nan
___四則演算のマーク___
+
-
*
/
|???|
|???|
_________________________________________
■ 指定した四則演算のキーを入力として、好きな2数を計算し、どのような四則演算を行ったかを出力できるようになりました。
■ 今度は、calcDice 配列の好きな2数を index で指定し、好きな四則演算のキー arithOpeNo に応じて、2数を計算した結果を格納した配列を出力する関数 renewDice() を定義していきます。
■ また、上記と同時に、calcDNames 配列の好きな2数を index で指定し、好きな四則演算のキー arithOpeNo に応じて、2数をどのように計算したかの記録を格納した配列を出力する関数 renewDNames() を定義していきます。
_____【 参考記事 】_____
4 Task005|Pythonのif文による条件分岐の書き方
➡︎ if文の書き方の中でも、特に条件式の改行について参考にした。
# [関数5] renewDice()
# ___入力1:サイコロ出目結果を計算要素として保存した配列 calcDices
# ___入力2:演算したい2数のインデックスのうちの1番目 ind1
# ___入力3:演算したい2数のインデックスのうちの2番目 ind2
# ___入力4:四則演算のうち何を使うかについて、指定する番号 arithOpeNo
# ___入力5:分数を許可するかどうかの選択オプション fracOption
# ___出力:2数を計算した結果を新たに格納した配列
###################################################
def renewDice(calcDice, ind1, ind2, arithOpeNo, fracOption):
newDice = np.copy(calcDice) #配列を上書きしないように calcDice のコピーを取得する
if newDice.shape[0] -1 > ind1 \
and newDice.shape[0] -1 > ind2 \
and ind1 != ind2:
#ind1,ind2がいずれもが白サイコロを示す範囲(0以上newDiceの長さ-2以下)にあり、ind1とind2が異なるとき
newDice[ind1] = arithOperator(newDice[ind1], newDice[ind2], arithOpeNo, fracOption)
#arithOpeNoで指定された四則演算を指定のインデックスの値に行う
else:
for i in range(newDice.shape[0] - 1):
newDice[i] = np.nan #すべての計算要素をnp.nanに置き換える
newDice = np.delete(newDice, ind2)
#共通して、ind2の値を削除し、サイコロ計算要素配列の長さを-1する
return newDice
# [関数6] renewDNames()
# ___入力1:サイコロ出目結果を文字化した配列 calcDNames
# ___入力2:演算したい2数のインデックスのうちの1番目 ind1
# ___入力3:演算したい2数のインデックスのうちの2番目 ind2
# ___入力4:四則演算のうち何を使うかについて、指定する番号 arithOpeNo
# ___入力5:分数を許可するかどうかの選択オプション fracOption
# ___出力:2数を計算した演算記録を残した配列
###################################################
def renewDNames(calcDNames, ind1, ind2, arithOpeNo, fracOption):
newDNames = np.copy(calcDNames) #配列を上書きしないように calcDNames のコピーを取得する
if newDNames.shape[0] - 1 > ind1 \
and newDNames.shape[0] -1 > ind2 \
and ind1 != ind2:
#ind1,ind2がいずれもが白サイコロを示す範囲(0以上newDiceの長さ-2以下)にあり、ind1とind2が異なるとき
newDNames[ind1] = '(' + newDNames[ind1] + arithMarker(arithOpeNo) + newDNames[ind2] + ')'
#arithOpeNoで指定された四則演算の記録を残す
else:
for i in range(newDNames.shape[0] - 1):
newDNames[i] = '|???|' #すべての計算要素の記録を|???|に置き換える
newDNames = np.delete(newDNames, ind2)
#共通して、ind2の値を削除し、サイコロ計算要素配列の長さを-1する
return newDNames
### fanction trial START ###
calcDice = transForCalc(jmcDice, printOption=True)
calcDNames = makeCalcName(calcDice, printOption=True)
print('\n___index=1, 4番目を掛け算で更新した計算要素の一覧___\n', renewDice(calcDice, 1, 4, arithOpeNo=2, fracOption=False))
print('___index=1, 4番目を掛け算で更新した文字化配列の一覧___\n', renewDNames(calcDNames, ind1=1, ind2=4, arithOpeNo=2, fracOption=False))
### fanction trial END ###
> 計算要素の一覧: [ 2. 3. 1. 4. 4. 55.]
> 文字化配列の一覧: ['2' '3' '1' '4' '4' '55']
>
> ___index=1, 4番目を掛け算で更新した計算要素の一覧___
> [ 2. 12. 1. 4. 55.]
> ___index=1, 4番目を掛け算で更新した文字化配列の一覧___
> ['2' '(3 * 4)' '1' '4' '55']
_________________________________________
■ 計算したい配列の index を2つ指定して、好きな四則演算を行い、計算要素の配列と計算記録の文字化配列を更新することができるようになりました。
■ そこで、いよいよジャマイカの解を全探索する関数を定義していきます。
■ 解探索では次のコンセプトを運用します。
[手順1] 白サイコロ5個の出目、つまり5個の整数値(1以上6以下)のうち、任意の2個を選んで並べ(5P2=20通りの組み合わせ)、四則演算(加減乗除で4種類)を行う。
[手順2] 上記[1]で生じた数1個と残りの3個の整数値(1以上6以下)のうち、任意の2個を選んで並べ(4P2=12通りの組み合わせ)、四則演算(加減乗除で4種類)を行う。
[手順3] 上記[1][2]と同様の流れで、1個の数字を出力するまで続ける。
■ したがって、解探索を行うために「再帰的に」配列を更新していく以下の関数を定義します。
[解探索する関数] jmcReduce()
___入力1:サイコロ出目結果を計算要素として保存した配列 calcDice
___入力2:サイコロ出目結果を文字化した配列 calcDNames
___入力3:分数を許可するかどうかの選択オプション fracOption
___出力:指定したインデックスの2数の四則演算結果で更新した calcDice と calcDNames を引数にもつ jmcReduce()
___反復:白サイコロに該当するインデックスのみを全探索する(2数のインデックスを i , j (i ≠ j)で走査)
___反復:2数を用いた四則演算のキーは 加・減・乗・除 を表す 0, 1, 2, 3 で全探索する(kで走査)
_____【 参考記事 】_____
5 Task005|再帰関数を理解するための最もシンプルな例
➡︎ 探索関数を再帰的に定義する際に、再帰関数の基本的な性質について理解し直すために参照した。
# [解探索する関数] jmcReduce()
# ___入力1:サイコロ出目結果を計算要素として保存した配列 calcDice
# ___入力2:サイコロ出目結果を文字化した配列 calcDNames
# ___入力3:分数を許可するかどうかの選択オプション fracOption
# ___出力:指定したインデックスの2数の四則演算結果で更新した calcDice と calcDNames を引数にもつ jmcReduce()
# ___反復:白サイコロに該当するインデックスのみを全探索する(2数のインデックスを i , j (i ≠ j)で走査)
# ___反復:2数を用いた四則演算のキーは 加・減・乗・除 を表す 0, 1, 2, 3 で全探索する(kで走査)
###################################################
def jmcReduce(calcDice, calcDNames, fracOption):
newDice = np.copy(calcDice) #入力1を改変しないために複製
newDNames = np.copy(calcDNames) #入力2を改変しないために複製
for i in range(newDice.shape[0] - 1): #インデックス1つ目を白サイコロの範囲(0以上newDiceの配列の長さ-2以下)でループ処理
for j in range(newDice.shape[0] - 1): #インデックス2つ目を白サイコロの範囲(0以上newDiceの配列の長さ-2以下)でループ処理
if i != j: #もしも ind1=i, ind2=j が等しくない場合
for k in range(4): #四則演算のキー番号 arithOpeNo = 0,1,2,3 を走査する反復変数 k
if arithOperator(newDice[i],newDice[j],k, fracOption) != np.nan: #演算結果が np.nan にならない場合のみ、配列を更新したい
if newDice.shape[0] == 3 \
and renewDice(newDice,i,j,k,fracOption)[0] == renewDice(newDice,i,j,k,fracOption)[1]:
#もし配列の長さが3、つまり白サイコロの計算要素の残り2つ、黒サイコロの和1つで構成されていて
#計算要素の四則演算の結果が、黒サイコロの和と一致するとき
print(renewDNames(newDNames,i,j,k,fracOption)[0], ' = ', renewDNames(newDNames,i,j,k,fracOption)[1],' ______!!!!! This pattern is OK !!!!!______')
#計算要素の計算記録(文字配列の値)を出力し、黒サイコロの値と一致したことを示す!(これが解のリスト)
break
elif newDice.shape[0] == 3 \
and renewDice(newDice,i,j,k,fracOption)[0] != renewDice(newDice,i,j,k,fracOption)[1]:
#もし配列の長さが3、つまり白サイコロの計算要素の残り2つ、黒サイコロの和1つで構成されていて
#計算要素の四則演算の結果が、黒サイコロの和と一致しないとき
#print(renewDNames(calcDNames,i,j,k,fracOption),' ___This pattern is NG xxx___')
#計算要素の計算記録(文字配列の値)を出力し、黒サイコロの値と一致しなかったことを示す!(見辛いので普通はコメントアウトする)
break
else: #まだ配列の長さが3より大きい場合
jmcReduce(renewDice(newDice,i,j,k,fracOption),renewDNames(newDNames,i,j,k,fracOption),fracOption)
#再帰的に、もう一度短い配列に更新してやり直す
else: #演算結果が np.nan になった場合は何もせずに k を更新する
continue
else: #もしも ind1=i, ind2=j が等しい場合は何もせずに j を更新する
continue
### fanction trial START ###
print('\n______START______')
jmcReduce(calcDice, calcDNames, fracOption=False)
### fanction trial END ###
______START______
(((2 + (4 * 4)) * 3) + 1) = 55 ______!!!!! This pattern is OK !!!!!______
(1 + ((2 + (4 * 4)) * 3)) = 55 ______!!!!! This pattern is OK !!!!!______
((3 * (2 + (4 * 4))) + 1) = 55 ______!!!!! This pattern is OK !!!!!______
(1 + (3 * (2 + (4 * 4)))) = 55 ______!!!!! This pattern is OK !!!!!______
((3 * ((4 * 4) + 2)) + 1) = 55 ______!!!!! This pattern is OK !!!!!______
(1 + (3 * ((4 * 4) + 2))) = 55 ______!!!!! This pattern is OK !!!!!______
(1 + (((4 * 4) + 2) * 3)) = 55 ______!!!!! This pattern is OK !!!!!______
((((4 * 4) + 2) * 3) + 1) = 55 ______!!!!! This pattern is OK !!!!!______
(((2 + (4 * 4)) * 3) + 1) = 55 ______!!!!! This pattern is OK !!!!!______
(1 + ((2 + (4 * 4)) * 3)) = 55 ______!!!!! This pattern is OK !!!!!______
((3 * (2 + (4 * 4))) + 1) = 55 ______!!!!! This pattern is OK !!!!!______
(1 + (3 * (2 + (4 * 4)))) = 55 ______!!!!! This pattern is OK !!!!!______
((3 * ((4 * 4) + 2)) + 1) = 55 ______!!!!! This pattern is OK !!!!!______
(1 + (3 * ((4 * 4) + 2))) = 55 ______!!!!! This pattern is OK !!!!!______
(1 + (((4 * 4) + 2) * 3)) = 55 ______!!!!! This pattern is OK !!!!!______
((((4 * 4) + 2) * 3) + 1) = 55 ______!!!!! This pattern is OK !!!!!______
_______END_______
第1戦目における考察
結果
■ 今回は再帰的に関数定義した jmcReduce()関数によって、徐々に配列を短く更新しながら、解を探索しました。
■ 結果としては、出力された解はどれも正しく、成り立つべきジャマイカの解を少なくともいくつかは提示できていると思います。
問題点
[1] 複数の解が数式の意味として重複している
■ 特に加算や乗算を用いた解の場合、数式的には同じ意味なのに、四則演算の順番を変更した解グループを複数表示してしまっていました。
例) (((2 + (4 * 4)) * 3) + 1) = 55 という解と
((((4 * 4) + 2) * 3) + 1) = 55 という解は、数式的には同じ意味です。
■ これを改善するには、加算(和,add()関数)や乗算(積,multiply())の扱いを変更しなければなりません。
[2] 全く同一の解を複数提示してしまっている
■ 今回の計算例では2グループの全く同一の解を提示してしまっていることがわかります。
例) ((((4 * 4) + 2) * 3) + 1) = 55 という解と
((((4 * 4) + 2) * 3) + 1) = 55 という解は、見た目も数式的意味も全く同一です。
■ おそらく、白サイコロの中に同じ数字が存在すると、再帰しているうちに何度も重複して演算結果を出してしまうのではないかと考えています。
[3] すべての解を探索できているのか?
■ ジャマイカの解は一般に、あるサイコロの組においてかなりの種類存在することが多いです。
■ その中に減算や除算を用いた解も、いくつか含まれているでしょう。
■ 今回のjmcReduceを何種類かのダイスロール結果で試していくうちに、「どうやら減算や除算を用いた解を探索できていないのではないか?」という疑念が湧いてきました。(特に除算)
■ そこで、以下の参考記事におけるジャマイカのダイスロール結果と解の例を用いて、jmcReduceを行ってみました。
例) 白サイコロ 2 4 2 4 5 黒サイコロ 20 3
に対して、解は例えば次の4通りが考えられる。
(加減乗除を満遍なく使えているパターンです。)
(2 × 6) + 2 + 4 + 5 = 23
((6 + 4) × 2) + 5 - 2 = 23
4 × (6 + (2 ÷ 2)) - 5 = 23
5 × (6 ÷ 2) + (4 × 2) = 23
_____【 参考記事 】_____
6 Check|ジャマイカの解探索の先行実装サイト
➡︎ ジャマイカの解探索を1つだけやってくれるサイト。(分数の利用オプション付き)
計算要素の一覧: [ 2. 6. 2. 4. 5. 23.]
文字化配列の一覧: ['2' '6' '2' '4' '5' '23']
______START______
((((2 * 6) + 2) + 4) + 5) = 23 ______!!!!! This pattern is OK !!!!!______
(5 + (((2 * 6) + 2) + 4)) = 23 ______!!!!! This pattern is OK !!!!!______
((((2 * 6) + 2) + 5) + 4) = 23 ______!!!!! This pattern is OK !!!!!______
(4 + (((2 * 6) + 2) + 5)) = 23 ______!!!!! This pattern is OK !!!!!______
((4 + ((2 * 6) + 2)) + 5) = 23 ______!!!!! This pattern is OK !!!!!______
===== 中略 中略 中略 =====
(5 + (2 + ((2 * 6) + 4))) = 23 ______!!!!! This pattern is OK !!!!!______
(((2 * 6) + 4) + (2 + 5)) = 23 ______!!!!! This pattern is OK !!!!!______
((2 + 5) + ((2 * 6) + 4)) = 23 ______!!!!! This pattern is OK !!!!!______
(2 + (5 + ((2 * 6) + 4))) = 23 ______!!!!! This pattern is OK !!!!!______
((5 + ((2 * 6) + 4)) + 2) = 23 ______!!!!! This pattern is OK !!!!!______
(((2 * 6) + 4) + (5 + 2)) = 23 ______!!!!! This pattern is OK !!!!!______
((5 + 2) + ((2 * 6) + 4)) = 23 ______!!!!! This pattern is OK !!!!!______
((((2 * 6) + 5) + 2) + 4) = 23 ______!!!!! This pattern is OK !!!!!______
(4 + (((2 * 6) + 5) + 2)) = 23 ______!!!!! This pattern is OK !!!!!______
((((2 * 6) + 5) + 4) + 2) = 23 ______!!!!! This pattern is OK !!!!!______
(2 + (((2 * 6) + 5) + 4)) = 23 ______!!!!! This pattern is OK !!!!!______
((2 + ((2 * 6) + 5)) + 4) = 23 ______!!!!! This pattern is OK !!!!!______
(4 + (2 + ((2 * 6) + 5))) = 23 ______!!!!! This pattern is OK !!!!!______
===== 中略 中略 中略 =====
(((5 + 4) + (2 * 6)) + 2) = 23 ______!!!!! This pattern is OK !!!!!______
((2 * 6) + ((5 + 4) + 2)) = 23 ______!!!!! This pattern is OK !!!!!______
(((5 + 4) + 2) + (2 * 6)) = 23 ______!!!!! This pattern is OK !!!!!______
((((2 + 2) * 6) - 5) + 4) = 23 ______!!!!! This pattern is OK !!!!!______
(4 + (((2 + 2) * 6) - 5)) = 23 ______!!!!! This pattern is OK !!!!!______
(((6 * (2 + 2)) - 5) + 4) = 23 ______!!!!! This pattern is OK !!!!!______
(4 + ((6 * (2 + 2)) - 5)) = 23 ______!!!!! This pattern is OK !!!!!______
((2 + 2) + ((6 * 4) - 5)) = 23 ______!!!!! This pattern is OK !!!!!______
(((6 * 4) - 5) + (2 + 2)) = 23 ______!!!!! This pattern is OK !!!!!______
((2 + 2) + ((4 * 6) - 5)) = 23 ______!!!!! This pattern is OK !!!!!______
(((4 * 6) - 5) + (2 + 2)) = 23 ______!!!!! This pattern is OK !!!!!______
((((2 * 2) * 6) - 5) + 4) = 23 ______!!!!! This pattern is OK !!!!!______
(4 + (((2 * 2) * 6) - 5)) = 23 ______!!!!! This pattern is OK !!!!!______
(((6 * (2 * 2)) - 5) + 4) = 23 ______!!!!! This pattern is OK !!!!!______
(4 + ((6 * (2 * 2)) - 5)) = 23 ______!!!!! This pattern is OK !!!!!______
((2 * 2) + ((6 * 4) - 5)) = 23 ______!!!!! This pattern is OK !!!!!______
(((6 * 4) - 5) + (2 * 2)) = 23 ______!!!!! This pattern is OK !!!!!______
((2 * 2) + ((4 * 6) - 5)) = 23 ______!!!!! This pattern is OK !!!!!______
(((4 * 6) - 5) + (2 * 2)) = 23 ______!!!!! This pattern is OK !!!!!______
((((2 + 4) * 2) + 6) + 5) = 23 ______!!!!! This pattern is OK !!!!!______
===== 中略 中略 中略 =====
((6 * 2) + (4 + (2 + 5))) = 23 ______!!!!! This pattern is OK !!!!!______
((4 + (2 + 5)) + (6 * 2)) = 23 ______!!!!! This pattern is OK !!!!!______
((2 * 6) + (4 + (2 + 5))) = 23 ______!!!!! This pattern is OK !!!!!______
((4 + (2 + 5)) + (2 * 6)) = 23 ______!!!!! This pattern is OK !!!!!______
((((6 - 2) * 4) + 2) + 5) = 23 ______!!!!! This pattern is OK !!!!!______
(5 + (((6 - 2) * 4) + 2)) = 23 ______!!!!! This pattern is OK !!!!!______
((((6 - 2) * 4) + 5) + 2) = 23 ______!!!!! This pattern is OK !!!!!______
(2 + (((6 - 2) * 4) + 5)) = 23 ______!!!!! This pattern is OK !!!!!______
((2 + ((6 - 2) * 4)) + 5) = 23 ______!!!!! This pattern is OK !!!!!______
(5 + (2 + ((6 - 2) * 4))) = 23 ______!!!!! This pattern is OK !!!!!______
(((6 - 2) * 4) + (2 + 5)) = 23 ______!!!!! This pattern is OK !!!!!______
((2 + 5) + ((6 - 2) * 4)) = 23 ______!!!!! This pattern is OK !!!!!______
(2 + (5 + ((6 - 2) * 4))) = 23 ______!!!!! This pattern is OK !!!!!______
((5 + ((6 - 2) * 4)) + 2) = 23 ______!!!!! This pattern is OK !!!!!______
(((6 - 2) * 4) + (5 + 2)) = 23 ______!!!!! This pattern is OK !!!!!______
((5 + 2) + ((6 - 2) * 4)) = 23 ______!!!!! This pattern is OK !!!!!______
(((6 - 2) * 4) + (2 + 5)) = 23 ______!!!!! This pattern is OK !!!!!______
((2 + 5) + ((6 - 2) * 4)) = 23 ______!!!!! This pattern is OK !!!!!______
((2 + 5) + (4 * (6 - 2))) = 23 ______!!!!! This pattern is OK !!!!!______
((4 * (6 - 2)) + (2 + 5)) = 23 ______!!!!! This pattern is OK !!!!!______
((2 + (4 * (6 - 2))) + 5) = 23 ______!!!!! This pattern is OK !!!!!______
===== 中略 中略 中略 =====
(((5 + 4) + 2) + (2 * 6)) = 23 ______!!!!! This pattern is OK !!!!!______
((6 * 2) + ((5 + 4) + 2)) = 23 ______!!!!! This pattern is OK !!!!!______
(((5 + 4) + 2) + (6 * 2)) = 23 ______!!!!! This pattern is OK !!!!!______
_______END_______
検証結果
■ 問題点[1][2]のために、非常に長い出力結果のため、途中を省略しました。
■ 結果として、減算を利用した解の出力はできていましたが、除算を利用した解の出力ができていませんでした。
■ 考えられる原因として、fracOptionの動作不良か、arithOperatorの定義のミスが考えられますが、Task.004にて四則演算の結果を出す際には、6/6も1と出力できていたので、正確な原因究明はできていません。
次回までの挑戦
[1] 加算・乗算の場合に、結果が同じものを予めパージする
■ 特に加算や乗算を用いた解の場合、数式的には同じ意味なのに、四則演算の順番を変更した解グループを複数表示してしまっていました。
■ add()関数やmultiply()関数、arithOprerator()関数の定義時、あるいはjmcReduce()関数のループ時に加算や乗算の結果が同一のi,jの組を予め排除する工夫を施せないでしょうか?
■ これについては、再帰的な関数定義によって求解するのが厳しいかもしれません。
■ 事前に考えられうる2数と四則演算の組み合わせの個数とその結果を出力した上で、探索しなければならない配列のセットをスタティック(静的)に格納したアレイを用意して、求解する方策も有効かと思いました。
[2] 除算のエラーを改善する
■ 正確な原因はわかりませんが、除算を利用した解の出力ができていませんでした。。
■ 四則演算関連の定義や、求解のあたりのアルゴリズムを見直しながら、正確な原因の究明から始めていきたいと思います。
次回予告
今回は、四則演算の関数定義と計算要素配列への再帰的走査関数を実装し、ジャマイカの求解に挑戦しました。
次回は、今回発生した問題を改善した上で、
再帰的探索を行わずに、スタティックに解候補を補完・生成・処理して、求解探索する関数を定義
することにも挑戦したいと思います。。
題して、vol.04 「ジャマイカの解探索を目指して〜第2戦目〜」 です。
REF. ジャマイカ関連の基本情報
Q1. 算数教具「ジャマイカ」って何?
A1. 「ジャマイカ / Jamaica」とは、サイコロを用いた"数遊び"を題材とする算数教具として販売されているものです。
■ AmazonやYahoo!ショッピングなどの通販サイトでも販売されている一般的な商品です。
➡︎ Amazon販売ページはこちらからどうぞ。
➡︎ 画像は下図を参照ください(上記ページからの引用)

■ サイコロは白と黒の2種類で、それぞれ5個と2個付属しています。
➡︎ 円環部分に白サイコロ×5個と黒サイコロ×1個、中央部分に黒サイコロ×1個が付属しています。
| 色 / Color | 数量 / amount | 記載されている数字 / Numbers |
|---|---|---|
| 白 / white | 5 個 / 5 dice | 1, 2, 3, 4, 5, 6 |
| 黒 / black | 1 個 / 1 dice | 1, 2, 3, 4, 5, 6 |
| 黒 / black | 1 個 / 1 dice | 10, 20, 30, 40, 50, 60 |
Q2. ジャマイカの遊び方は?
A2. 白サイコロ×5個の数字をそれぞれ1回ずつ使って四則演算を行い、黒サイコロ×2個の数字の和を作ります。
例えば、白サイコロの出目が(1,2,3,5,5)であり、黒サイコロの出目が(10,6)の場合は、
白サイコロの出目を全て足し合わせて 1+2+3+5+5=10+6 という等式を作ることができます。
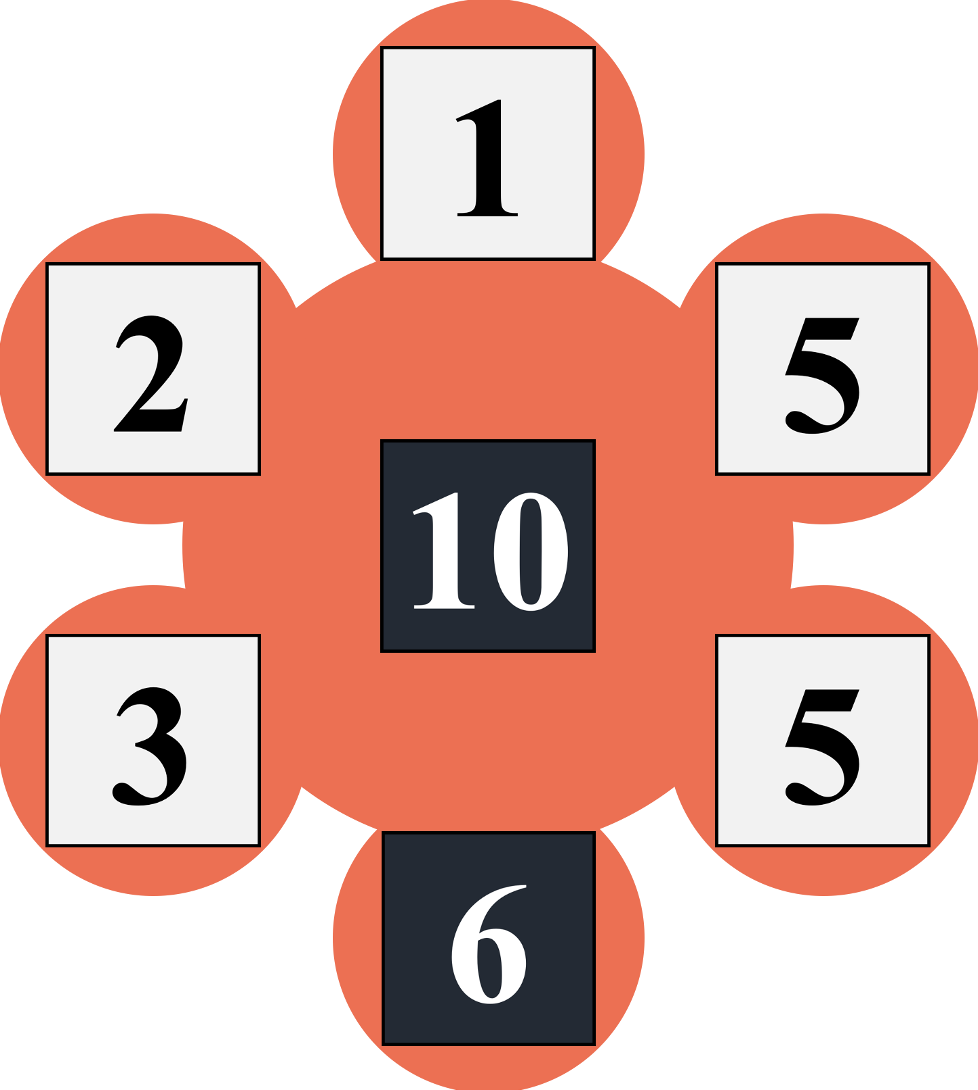
■ 白サイコロ×5個の数字は、それぞれ1回ずつしか使えません。
➡︎ 例えば、白サイコロの出目が(2,4,5,3,3)だった場合、計算に使えるのは
2 が1回、3 が2回、4 が1回、5 が1回です。それ以上使ってはいけません。
(2 を2回使ったり、3 を3回使ったりしてはダメです。)
➡︎ もちろん、「指定回数分使わない」ことも御法度です。
(上の例では、3 を1回しか使わないなどもダメです。)
■ 四則演算とは、加減乗除のことです。
➡︎ 「加」とは、「加法」すなわち**「足し算」です。
例えば、2+3=5 のような和(足し算の結果)を計算します。
➡︎ 「減」とは、「減法」すなわち「引き算」です。
例えば、5-2=3 のような差(引き算の結果)を計算します。
➡︎ 「乗」とは、「乗法」すなわち「掛け算」です。
例えば、3×4=12 のような積(掛け算の結果)を計算します。
➡︎ 「除」とは、「除法」すなわち「割り算」**です。
例えば、4÷2=2 のような商(割り算の結果※)を計算します。
※ 割り切れる演算のみを許す、すなわち既約分数形を許さないルールと、既約分数も許すルールがあります。
[1] 既約分数になるものは許さないルールの場合
白サイコロの出目(2,4,6,3,5)のとき、6÷3=2 という演算はできますが、
6÷4=3/2 という結果は利用不可能です。
[2] 既約分数になるものも許すルールの場合
白サイコロの出目(2,4,6,3,5)のとき、6÷3=2 という演算もできるだけでなく、
6÷4=3/2 という結果も利用可能です。
※ 既約分数を利用しないと解けないサイコロの出目の組もあります。
例) 白サイコロの出目(2,2,4,4,6)に対して、黒サイコロの出目(30,3)のとき
{(2- 2/4) + 4} × 6 = 30 + 3 という等式が成り立ちます。
■ 四則演算はどのような順番で行っても構いません。
➡︎ 先に2つの数字を足しておいて、別の数字と掛ける、といった演算の順序は自由です。
つまり、いつ・どこでも括弧を何回使ってもよいということです。
例) 白サイコロの出目(3,6,4,4,1)に対して、黒サイコロの出目(20,6)のとき
{(3 + 6) + (4 × 4)} + 1 = 20 + 6 という等式が成り立ちます。
参考記事まとめ
-
Recollection|算数教具「ジャマイカ」を再現しよう❗️の前々回記事(vol.01) ↩
-
Recollection|算数教具「ジャマイカ」を再現しよう❗️の前回記事(vol.02) ↩
-
Task004|【NANって何だ?】意味と用法 ↩
-
Task005|Pythonのif文による条件分岐の書き方 ↩
-
Task005|再帰関数を理解するための最もシンプルな例 ↩
-
Check|ジャマイカの解探索の先行実装サイト ↩
