はじめに

このシリーズは、とある算数教具「ジャマイカ」について、
以下の目的を達成するべく奮闘する記録です。

▶︎　1. 「ジャマイカ」のゲームを画像表示などを用いたプログラムで動かせるようになる。
2. 「ジャマイカ」におけるサイコロの任意の組み合わせについて、解の存在とその内容を探索・提示するプログラムを作る。

Q1. 算数教具「ジャマイカ」って何？

A1. 「ジャマイカ / Jamaica」とは、サイコロを用いた"数遊び"を題材とする算数教具として販売されているものです。

■ AmazonやYahoo!ショッピングなどの通販サイトでも販売されている一般的な商品です。
　➡︎ Amazon販売ページはこちらからどうぞ。
　➡︎ 画像は下図を参照ください（上記ページからの引用）

　➡︎ 出版社などの詳細な情報は下表を参照ください（上記ページからの引用）

カテゴリ / Category	情報 / Information
出版社 / publisher	トモエ算盤(2006/12/8)
言語 / language	日本語 / Japanese
ISBN-10	4902756161
ISBN-13	978-4902756166
発売日 / release date	2006/12/8
梱包サイズ / packing size	13 × 10.6 × 2 cm

■ サイコロは白と黒の２種類で、それぞれ５個と２個付属しています。
　➡︎ 円環部分に白サイコロ×５個と黒サイコロ×１個、中央部分に黒サイコロ×１個が付属しています。

色 / Color	数量 / amount	記載されている数字 / Numbers
白 / white	5 個 / 5 dice	1, 2, 3, 4, 5, 6
黒 / black	1 個 / 1 dice	1, 2, 3, 4, 5, 6
黒 / black	1 個 / 1 dice	10, 20, 30, 40, 50, 60

Q2. ジャマイカの遊び方は？

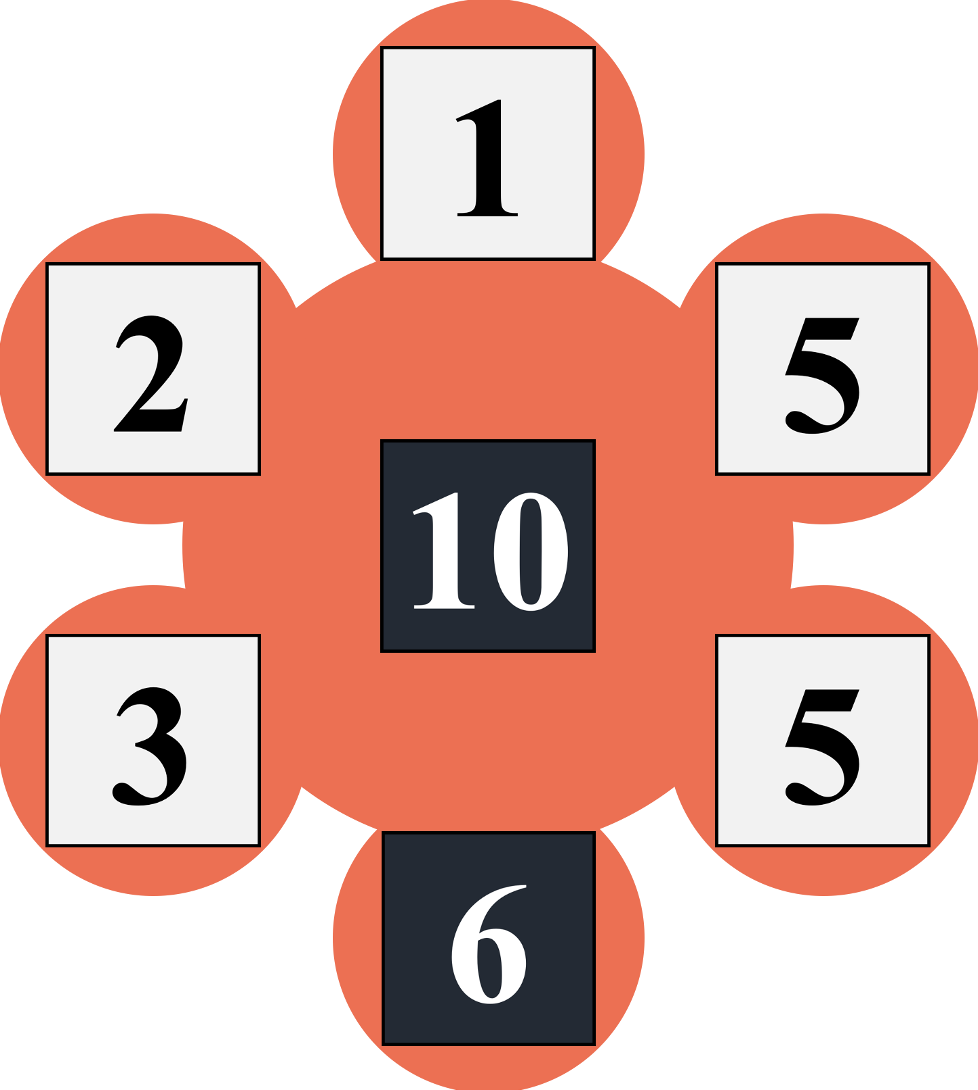
A2. 白サイコロ×５個の数字をそれぞれ１回ずつ使って四則演算を行い、黒サイコロ×２個の数字の和を作ります。

例えば、白サイコロの出目が（1,2,3,5,5）であり、黒サイコロの出目が（10,6）の場合は、
白サイコロの出目を全て足し合わせて 1+2+3+5+5=10+6 という等式を作ることができます。

■ 白サイコロ×５個の数字は、それぞれ１回ずつしか使えません。
　➡︎ 例えば、白サイコロの出目が（2,4,5,3,3）だった場合、計算に使えるのは
　　　2 が１回、3 が２回、4 が１回、5 が１回です。それ以上使ってはいけません。
　　　（2 を２回使ったり、3 を３回使ったりしてはダメです。）
　➡︎ もちろん、「指定回数分使わない」ことも御法度です。
　　　（上の例では、3 を１回しか使わないなどもダメです。）

■ 四則演算とは、加減乗除のことです。
　➡︎ 「加」とは、「加法」すなわち「足し算」です。
　　例えば、2+3=5 のような和（足し算の結果）を計算します。
　➡︎ 「減」とは、「減法」すなわち「引き算」です。
　　例えば、5-2=3 のような差（引き算の結果）を計算します。
　➡︎ 「乗」とは、「乗法」すなわち「掛け算」です。
　　例えば、3×4=12 のような積（掛け算の結果）を計算します。
　➡︎ 「除」とは、「除法」すなわち「割り算」です。
　　例えば、4÷2=2 のような商（割り算の結果※）を計算します。
　※ 割り切れる演算のみを許す、すなわち既約分数形を許さないルールと、既約分数も許すルールがあります。
　　[1]　既約分数になるものは許さないルールの場合
　　　　　白サイコロの出目（2,4,6,3,5）のとき、6÷3=2 という演算はできますが、
　　　　　6÷4=3/2 という結果は利用不可能です。
　　[2]　既約分数になるものも許すルールの場合
　　　　　白サイコロの出目（2,4,6,3,5）のとき、6÷3=2 という演算もできるだけでなく、
　　　　　6÷4=3/2 という結果も利用可能です。
　※ 既約分数を利用しないと解けないサイコロの出目の組もあります。
　　例）白サイコロの出目（2,2,4,4,6）に対して、黒サイコロの出目（30,3）のとき
　　　　{(2- 2/4) + 4} × 6 = 30 + 3 という等式が成り立ちます。

■ 四則演算はどのような順番で行っても構いません。
　➡︎ 先に２つの数字を足しておいて、別の数字と掛ける、といった演算の順序は自由です。
　　つまり、いつ・どこでも括弧を何回使ってもよいということです。
　　例）白サイコロの出目（3,6,4,4,1）に対して、黒サイコロの出目（20,6）のとき
　　　　{(3 + 6) + (4 × 4)} + 1 = 20 + 6 という等式が成り立ちます。

§1. 「ジャマイカ」を再現する

ジャマイカという遊具を買って以来、実物を用いて行うのが楽しいと思いつつも、次第に
「コードで再現したい……」
「オンラインミーティングの画面共有とかで一緒にやりたい……」
と思うようになりました。

そこで、初のQiita投稿もしてみたいという気持ちを相まって、今回のシリーズが生まれました。

シリーズタイトルは、
算数教具「ジャマイカ」を再現しよう❗️
です。

コーディング初心者がジャマイカを再現するべく奮闘する記録をよしなにご覧ください。

《特記事項》
[1] このシリーズは、GoogleColabratory というサービスを利用して JupyterNotebookファイル(.ipynb) で試行錯誤した結果を整えて掲載しています。
[2] Python のバージョンは 3.6.9 です。これは以下のコードを利用して確認しました。

confirmPythonVer

import platform
print('python ' + platform.python_version())

> python 3.6.9

↑↑↑ 上記コードの参考URLはこちらから ¹
[3] その他の必要となるライブラリについては、使用時に都度記載していきます。

Task.001 「サイコロの出目を画像で表示する」

■ リアルなジャマイカでは、２色のサイコロを計７個用いる。
■ サイコロの色や数字などの内訳は以下の通り。（再掲）

色 / Color	数量 / amount	記載されている数字 / Numbers
白 / white	5 個 / 5 dice	1, 2, 3, 4, 5, 6
黒 / black	1 個 / 1 dice	1, 2, 3, 4, 5, 6
黒 / black	1 個 / 1 dice	10, 20, 30, 40, 50, 60

■ このサイコロの出目を画像で表示したい。

　手順1.　サイコロの画像を用意する。(今回はMicrosoftPowerPointで作成した。拡張子は.png)
　手順2.　サイコロの画像をGoogleDriveの所定のフォルダに保存する。
'/content/drive/My Drive/Mathematics/MathProgramming/MathPro-Jamaica/Jamaica-figs/'
　手順3.　用意したサイコロの画像をそれぞれ試しに表示してみる。
　　　　　↓↓↓ 具体的なファイル名は以下を参照のこと。

ファイル名：　　'dice-' '色(白=w, 黒=b)' '-' '番号（1-6, 10-60）' '.png'
例) dice-w-4.png　= 白サイコロの4
例) dice-b-20.png = 黒サイコロの20

＿＿＿＿＿【参考記事】＿＿＿＿＿
² Task001｜Pythonで画像を表示する方法
　➡︎ 画像表示の基礎的な文法はここから引用した。
³ Task001｜画像をグリッド状に並べて軸ラベルを消す
　➡︎ 複数枚画像を一覧で並べて表示する方法として、一番良さそうなコードが乗っていた記事。

task001_black10

import matplotlib
import matplotlib.pyplot as plt
import matplotlib.image as mpimg

wheredrive = '/content/drive/My Drive/Mathematics/MathProgramming/MathPro-Jamaica/'
wherefigs = wheredrive + 'Jamaica-figs/'
whereimg = wherefigs + 'dice-b-10.png'
print('画像ファイルの参照先： ',whereimg)
img = mpimg.imread(whereimg)
imgplot = plt.imshow(img)
plt.axis('off') #'on'にすると画像１つ１つに縦横のグリッド軸が追加で表示される

> 画像ファイルの参照先：  /content/drive/My Drive/Mathematics/MathProgramming/MathPro-Jamaica/Jamaica-figs/dice-b-10.png

task001_white1to6

import numpy as np

row = 1 #画像を表示する枠行列における行の数
col = 6 #画像を表示する枠行列における列の数
plt.figure(figsize=(10,10)) #画像１つ１つのサイズを調整するパラメータの指定
for num in range(row * col):
    plt.subplot(row, col, num+1) #このループで画像を表示する枠の作成
    imgname = 'dice-w-' + str(num+1) + '.png'
    whereimg = wherefigs + imgname
    img = mpimg.imread(whereimg)
    imgplot = plt.imshow(img)
    plt.axis('off') #'on'にすると画像１つ１つに縦横のグリッド軸が追加で表示される

Task.002 「ランダムな数字に合わせてサイコロ出目画像を表示する」

■ リアルなジャマイカでは、サイコロをランダムに振る。
■ 全部で７個のサイコロを振る操作を、ランダムな数字の出力で代行する。
　手順1.　1以上6以下の正の整数をランダムに出力する変数を７個用意する。
　手順2.　前半の１〜５個目の結果を白サイコロの画像表示に対応づける。
　手順3.　6個目の結果を2桁の黒サイコロの画像表示に対応づける。
　手順4.　7個目の結果を1桁の黒サイコロの画像表示に対応づける。

＿＿＿＿＿【参考記事】＿＿＿＿＿
⁴ Task002｜Pythonでランダムな小数・整数を生成するrandom, randrange, randintなど
　➡︎ 乱数生成に関して、いろいろなモジュールが見れるので、整理するには良い。
⁵ Task002｜いろんなサイコロが作れるrandint
　➡︎ 誰もが気になるサイコロの事象確率が同様に確からしいかどうか、確かめてくれている。

task002_diceroll

row = 1 #画像を表示する枠行列における行の数
col = 7 #画像を表示する枠行列における列の数
dices = np.random.randint(1,7,row * col) #第１変数は母集団の最小値、第2変数は母集団の最大値+1、第3変数はランダムな数字の出力する個数
print('サイコロ７個の結果',dices)

plt.figure(figsize=(20,20))
for index in range(row * col):
  plt.subplot(row, col, index+1)
  if index < 5: #5個目まで（indexが0以上4のとき）のサイコロは白で1桁
    imgname = 'dice-w-' + str(dices[index]) + '.png'
    whereimg = wherefigs + imgname
    img = mpimg.imread(whereimg)
    imgplot = plt.imshow(img)
    plt.axis('off')
  elif index < 6: #6個目（indexが5のとき）のサイコロは黒で2桁
    imgname = 'dice-b-' + str(dices[index]) + str(0) + '.png'
    whereimg = wherefigs + imgname
    img = mpimg.imread(whereimg)
    imgplot = plt.imshow(img)
    plt.axis('off')
  elif index < 7: #7個目（indexが6のとき）のサイコロは黒で1桁
    imgname = 'dice-b-' + str(dices[index]) + '.png'
    whereimg = wherefigs + imgname
    img = mpimg.imread(whereimg)
    imgplot = plt.imshow(img)
    plt.axis('off')
  else:
    continue

> サイコロ７個の結果 [6 5 1 4 2 4 3]

次回予告

今回は主に、Pythonで画像を表示する方法と、サイコロのランダムな出目をシミュレートする方法の備忘録を記載しました。

次回は、これらのコードを関数定義によって整理する備忘録です。

題して、vol.02 「Pythonで関数を作るための備忘録」 です。

参考記事まとめ

Demo｜colaboratoryにデフォルトで入っているライブラリのバージョン情報を確認する ↩
Task001｜Pythonで画像を表示する方法 ↩
Task001｜画像をグリッド状に並べて軸ラベルを消す ↩
Task002｜Pythonでランダムな小数・整数を生成するrandom, randrange, randintなど ↩
Task002｜いろんなサイコロが作れるrandint ↩

算数教具「ジャマイカ」を再現しよう❗️ vol.01 「Pythonで画像を表示するための備忘録」