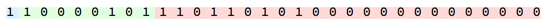はじめに
一昨日の記事 で、Wolframコミュニティで答えた質問を紹介しましたが、本記事ではその回答について説明します。
質問
質問の内容はこうです。
とあるシステムで浮動小数点数を扱ってます。Mathematicaで浮動小数点のバイナリ列が正しいかどうか確認したいんですが、どうやって確認したらいいですか?
(超意訳)
ということで、Mathematicaで浮動小数点数のバイナリ列を扱う方法を紹介します。
回答
Mathematicaでは、単精度数(32ビット浮動小数点数)は Real32 として扱われます。
適当な数字を ExportString すればバイナリを得ることができるのですが、バイナリゆえに表示上は文字化けします。
In[1]:= ExportString[12345, "Real32"]
Out[1]= ä@F
そこで、バイナリをさらに ImportString で UnsignedInteger32 として読み込み、それを2進数としてリスト化すれば、文字化けしない状態の列を得ることができます。
(* 数値をIEEE 754 の単精度浮動小数点数表現の01列 (長さ32) に変換 *)
real32Digits[x_] :=
IntegerDigits[
First[ImportString[ExportString[x, "Real32"], "UnsignedInteger32"]],
2, 32]
(* Real32で表された01列から {sgn, e, m} のリストを生成 (特別な数は無視) *)
real32Format[li_] :=
{If[First[li] === 0, 1, -1],
FromDigits[Take[li, {2, 9}], 2] - 2^7 + 1,
FromDigits[{Join[{1}, Take[li, {10, 32}]], 1}, 2]}
(* Real32で表された01列をそれの表す数値に変換 *)
fromReal32Digits[li_] := First[ImportString[ExportString[FromDigits[li, 2], "UnsignedInteger32"], "Real32"]]
ちなみに用語としては
sgn: Sign(符号)
e: Exponent part(指数部)
m: Mantissa(仮数部)
を意味します。略し方は文献によってまちまちなのであまり信用しないでください(仮数はSignificandとも書くので、こっちをsと略す場合もあります。)。
これをつかっていろいろな浮動小数点数をリスト化してみましょう。
In[1] := real32Digits[-118.625]
Out[1] := {1, 1, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 1, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0}
In[2]:= real32Format[%]
Out[2] := {-1, 6, 949/512}
In[3] := fromReal32Digits[%%]
Out[3] := -118.625
In[1]: real32Digits[Pi]
In[2]: real32Format[%]
In[3]: fromReal32Digits[%%]
In[4]: N[%]
Out[1]: {0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1, 1, 1,
1, 1, 1, 0, 1, 1, 0, 1, 1}
Out[2]: {1, 1, 13176795/8388608}
Out[3]: 3.14159
Out[4]: 3.14159
In[1]: real32Digits[2^128]
In[2]: real32Format[%]
In[3]: fromReal32Digits[%%]
In[4]: fromReal32DigitsByAbnormal[%%%]
Out[1]: {0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0}
Out[2]: {1, 128, 1}
Out[3]: Infinity
Out[4]: 340282366920938463463374607431768211456
In[1]: real32Digits[0]
In[2]: real32Format[%]
In[3]: fromReal32Digits[%%]
Out[1]: {0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0}
Out[2]: {1, -127, 1}
Out[3]: 0.
上記の方法だと、符号部・指数部・仮数部が並んで表示されているので、区切りがわかりにくいですね。
そこで、符号部が青、指数部が緑、仮数部が赤にハイライトされる仕組みも作りました。
nLi = IntegerDigits[First[ImportString[ExportString[-118.625, "Real32"], "UnsignedInteger32"]], 2, 32]
sgnLi = Take[nLi, 1]; (* Sign *)
eLi = Take[nLi, {2, 9}]; (* Exp *)
sLi = Take[nLi, {10, 32}]; (* Mantissa *)
Grid[{Join @@ {Item[#, Background -> LightBlue] & /@ sgnLi,
Item[#, Background -> LightGreen] & /@ eLi,
Item[#, Background -> LightRed] & /@ sLi}}]
どうでしょう。これでややこしい浮動小数点数への理解が深まれば幸いです。
最後に
ちなみに、 Real64、 Real128 でも同じことをやっているので、ご興味ある方いればお教えいたします。
(ToDoとしてはComplex64 …。)