自己紹介
関東圏の大学の文系学部に通うものです。最近よくよく考えると誤差逆伝播(数式の変形を追っただけ)やDeconvolutionなどの原理をよく知らないということを悟り、調べたらみんなあまり詳しく解説していないような気がしたので、改めてまとめようと思いここに書きました。
どのような人向けの記事か
・全結合層ネットワークでの誤差逆伝播をある程度理解している人
・CNNの順伝播(畳み込みの計算など)をある程度理解している人
・CNNの逆伝播もしくはDeconvolutionの仕組みを知りたい人
(「Decovolutionの計算はCNNの誤差逆伝播とほぼ同じだよ」といってすぐに理解できた人は、最後の補足だけみてくだされば大丈夫だと思います。)
なぜこのタイミングでCNNの誤差逆伝播の説明?
これを読んでくださっている皆さん、いまの時代chainer, TensorFlow, Keras, PyTorchなど、どのフレームを使っているかは個人の自由ですが、基本的に抽象化されたフレームワークを使用していると思います。そうなるときっと1から誤差逆伝播を記述する機会は少なくなっているのではないでしょうか。(と言いますか、僕は恥ずかしながら書いたことありませんでした。)
chainer風に記述すれば、Lossの計算をしてLoss.backward()すれば誤差逆伝播できるのでそこまで気にする必要もないかもしれません。しかし、このようにこれから便利になっていくことが予期されるからこそ、一回ちゃんと原理を抑えようと思い、この記事を書きました。
皆さん本当にCNNの誤差逆伝播を理解していますか?(煽りと戒め)
僕は今までゼロから作るDeepLearning を読んでわかった気になっていました(全結合層の誤差逆伝播は抑えたし、CNNもどうせ同じようなものだろうと…)。もちろんこの書籍は初学者に対して、非常にわかりやすく記述されており、名著であると個人的に思っています。しかし、皆さんお気づきでしょうか?あの本はあくまで初学者向きであり、誤差逆伝播の計算の代わりに数値微分を用いていていることに…
すみません、ここの記述は誤りがありました。ゼロから作るDeepLearningは、ソースコードの方にBackwardの処理も記述しており、誤差逆伝播で解いていました(大変失礼しました)。
本記事は、先の教科書とは異なり(計算量を気にせず)数式の動きを解説した記事、もしくはDeconvolutionの挙動とConvolutionのBackwardの挙動の比較を書いた記事として読んでいただけると幸いです。(2018/08/22)
Deconvolutionとの関係
CNNの逆伝播の仕組みを理解することは、Deconvolutionの計算過程を理解することに繋がります。これはどういうことを言っているかと言いますと、chainerの場合は、Convolutionの計算の誤差逆伝播にはDeconvolutionを用いており、逆もまた然りとなっているからです。つまり、Convolution層に返ってきた特徴マップ上の誤差をDeconvolutionすることでもう一つ前の層に誤差を伝えています。しかも、Deconvolutionは教科書にはあまり乗っていないと思いますし、なにをやっているかわかりにくいので、ここで一度把握しておくべきかと考えたからです。ただ大きく異なると言いますか、注意しなければいけないことは、Deconvolutionによる特徴マップの拡大は順伝播の際に行われるものであり、誤差逆伝播で行われる特徴マップの拡大させる処理は逆伝播であるため、活性化関数の扱いが異なるということです。
Deconvolutionの動きなどは、こちらの記事を見ていただけるとわかりやすいと思います。
・Convolution arithmetic
数式的な理解とイメージ的な理解
数式的な展開とイメージ的な理解がつながれば幸いですが、本当に詳しいことが知りたいかたは画像認識 (機械学習プロフェッショナルシリーズ)を参考にしてみてください。
順伝播
CNNの順伝播の場合の畳み込みの計算は、以下のサイトなどが非常にわかりやすいですし、ゼロから作るDeepLearning にも乗っているので割愛します。
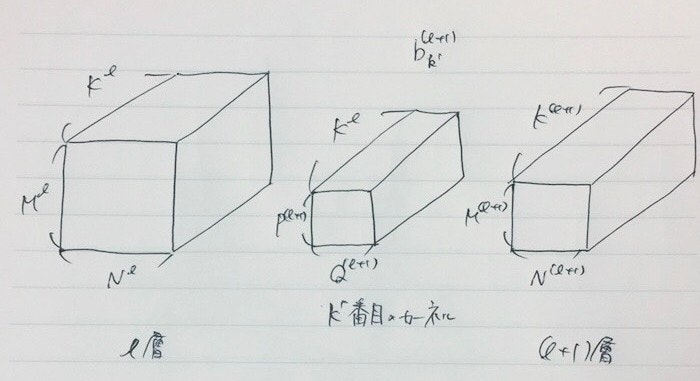
====変数の定義=====
$K^l$:l層のチャンネル数(lは添字)
$M^l,N^l$:l層の縦横の長さ
$P^{l+1},Q^{l+1}$:カーネルの縦横の長さ
$p = ${$1,2,...,P^{l+1}$}
$q = ${$1,2,...,Q^{l+1}$}
$k = ${$1,2,...,K^{l}$}
$k'= ${$1,2,...,K^{l+1}$}
=================
$
a _ { m , n , k ^ { \prime } } ^ { l + 1 } = \sum _ { p , q , k } w _ { p , q , k,k^{'} } ^ { l + 1 } z _ { m + p , n + q , k } ^ { l } + b _ { k ^ { \prime } } ^ { l + 1 }
$
$
z _ { m , n , k ^ { \prime } } ^ { l } = h \left( a _ { m , n , k ^ { \prime } } ^ { l } \right)
$
$a _ { m , n , k ^ { \prime } } ^ { l + 1 } $ :(l+1)層上のピクセル(m,n)におけるk'番目のチャンネルにおける出力
$w _ { p , q , k,k^{'} } ^ { l + 1 } $ :(l+1)層の特徴マップを作成するために使用したカーネルのうちk'番目のカーネルであり、kチャンネル目にある(p,q)の位置にある重み
$z _ { m + p , n + q , k } ^ { l }$ :l層上のピクセル(m+p,n+q)におけるkチャンネル目の出力
$b _ { k ^ { \prime } } ^ { l + 1 }$ :各チャンネル毎のバイアス項
$h(x)$ :活性化関数(ReLUなどなど)
以下のサイトなども参考になります。
・Convolution arithmetic
・Convolutional Neural Networkとは何なのか
・Applied Deep Learning - Part 4: Convolutional Neural Networks
逆伝播
逆伝播は、連鎖律という規則を用いて各パラメータでの勾配を計算していきます。CNNのConvolution層でも、もちろんそれは変わりません。ただConvolution層の場合は順伝播で、カーネル(フィルターとも呼ばれる)という重みテンソル(この記事では多次元配列のことをテンソルと呼ぶ)を共有することで、対象にした特徴マップから次の層の特徴マップを作成しています。そしてこの計算過程をもとに逆伝播させていくわけですから、全結合層とは少し勝手が異なります。
このように重みの共有の問題を乗り越え、誤差逆伝播を計算するためには3つ問題点に上がると思われます。
1.誤差逆伝播の計算について
2.どのようにして、特徴マップのサイズ(縦と横の大きさ)を大きくしているのか?
3.どのようにして、特徴マップのチャンネル数の違いを合わせているのか?
1.誤差逆伝播の計算について
全結合層での誤差逆伝播の計算はこれらの記事、「誤差逆伝播法のノート」、「誤差逆伝播法をはじめからていねいに」を見ていただければわかると思いますので、 ここでは省略します。
イメージ的には、「重み行列(行列)→カーネル(テンソル)」、「中間層(ベクトル)での発火→特徴マップ(テンソル)での発火」に変わります。ただ、全結合ではないので、ある特徴マップでの1点の発火が、次の層の特徴マップに関与している訳ではないことに注意する必要もあります(有効受容野の考えに近いものですね)。
2.どのようにして、特徴マップのサイズ(縦と横の大きさ)を大きくしているのか?
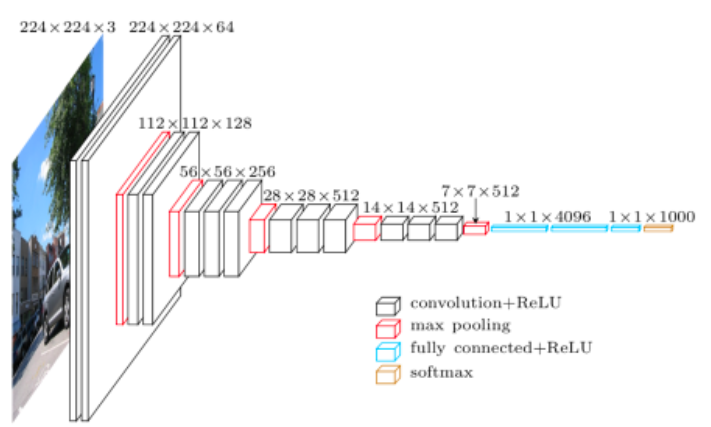
順伝播の場合は畳み込みの計算でpaddingサイズやstrideサイズ、dilateなどを指定することで特徴マップのサイズ(縦横の大きさ)を調整しています。ResNetなどのモデルでは特徴マップのサイズが変わりませんが、VGG-16などのモデルをイメージしていただければ、徐々に特徴マップが小さくなっていく様子がわかると思います。ちなみにサイズの調整に関しては、このサイト【保存版】chainerのconvolutionとdeconvolution周りを理解するがわかりやすいと思います。ただこの記事はあくまで1チャンネルで動かした際のDeconvolutionの計算をわかりやすく、具体的に説明してくれているということに注意する必要があります。そしてこの記事を踏まえた上で今回は解説を行います。
まず、逆伝播の計算では特徴マップ上に帰ってきた勾配に対して畳み込みの計算を行います。ただ、通常の順伝播での畳み込み計算ではなく、勾配に対してDeconvolution(逆畳み込み)を行います。しかし、Deconvolution(逆畳み込み)と言っても特別新たな計算を行うという訳ではありません。では何が順伝播(Convolution)と計算過程が異なるかと言いますと、以下の点です。
2.① 重み行列を縦横方向に反転する
2.② 1チャンネルごとに計算を行う
(順伝播の畳み込みの計算はカーネルごとにチャンネル方向にも一気に足し合わせてしまうが、逆伝播では各チャンネルごとに全てのカーネルを用いて計算を行うことが違う)
2.③ サイズを調整するためにzero-paddingやdilateなどを駆使する
2.①重み行列(使用する重みテンソルのあるチャンネル)を縦横方向に反転する
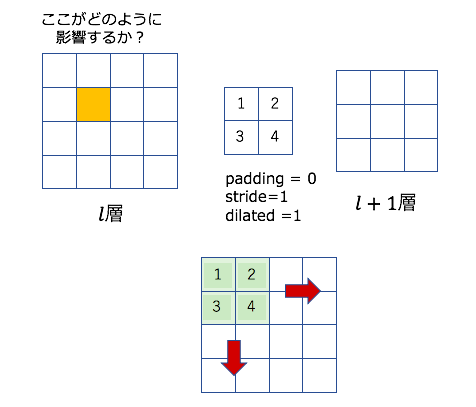
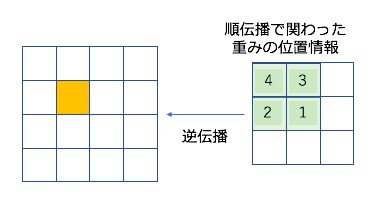
これはなぜこのようなことをしているかを理解するためには、まずはじめに順伝播で関わったピクセルと重みの位置を意識する必要があります。以下のように4×4の特徴マップから2×2のカーネル(単純のためにチャネル数は1になっている)から3×3の特徴マップの順伝播を考えます。ここでのカーネルの数字は重みの大きさというよりは、位置情報という風に読んでくださると理解が捗るかもしれません。
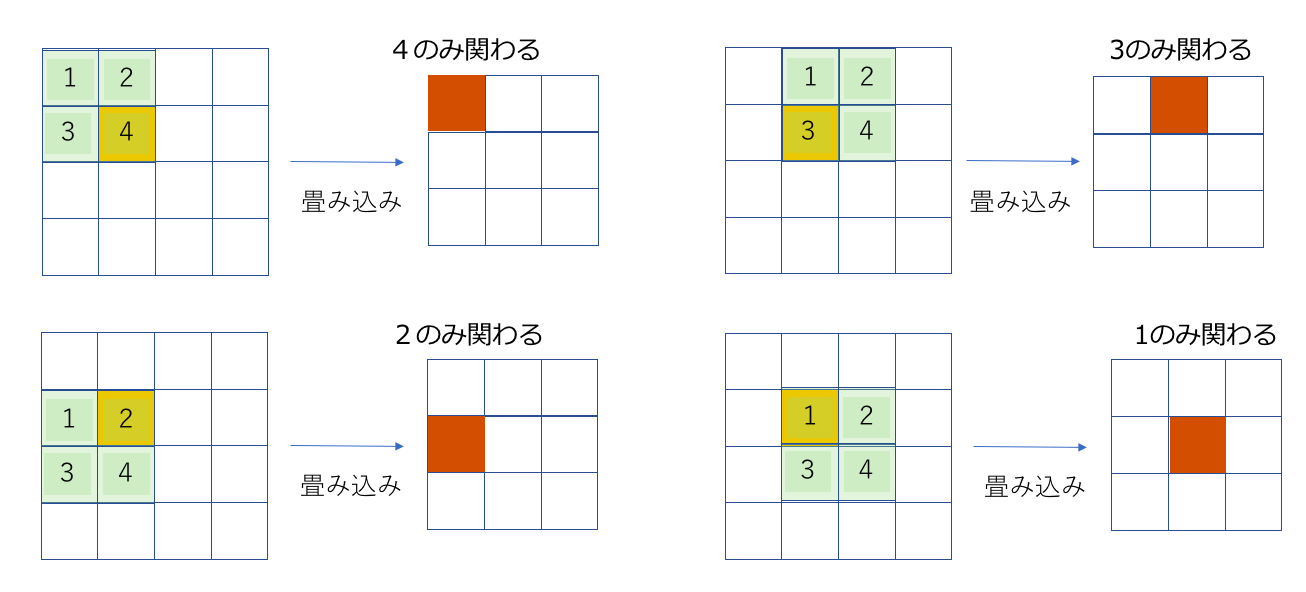
すると、各畳み込み処理の結果と、携わった重み行列の要素は以下のようになります。今回はオレンジ色になっているピクセルの計算に関わらない計算は無視してあります。
つまり、3×3の特徴マップを作るために、カーネルが関わった重みの要素の情報と3×3の特徴マップのピクセルの関係は以下のようになります。
順伝播の際に関わった重みの位置は、ちょうどカーネルの縦横を反転させたものと一致します。このようにして、オレンジ色のピクセルが計算に関わった重み要素と特徴マップの箇所に対して逆伝播を行うことができるということになります。じゃあ、l層の(1,1)番目のピクセルの逆伝播はどうするんだ?という疑問を思った方は、2.③をご覧ください。有り体に言うと、辻褄が合うようにpadding等をすればいいと言う話なだけです。
2.②どのようにして、特徴マップのサイズ(縦と横の大きさ)を大きくしているのか?
これは順伝播の時と逆伝播の時の数式を見てもらえば一目瞭然なのですが、まず順伝播の時の計算式は以下です(stride=1,padding=0の時)。(デルタの計算の時に戻ってきます。)
$
a _ { m , n , k ^ { \prime } } ^ { l + 1 } = \sum _ { p , q , k } w _ { p , q , k,k^{'} } ^ { l + 1 } z _ { m + p , n + q , k } ^ { l } + b _ { k ^ { \prime } } ^ { l + 1 }
$
$
z _ { m , n , k ^ { \prime } } ^ { l } = h \left( a _ { m , n , k ^ { \prime } } ^ { l } \right)
$
次に逆伝播の時の計算です。
逆伝播を行う目的としては、各層のカーネルの重みを更新することにあります。そこで必要なものは、$\frac { \partial J _ { i } } { \partial w _ { p , q , k , k ^ { \prime } } ^ { l } }$となります。連鎖律を元にこの勾配を計算すると以下のようになります。
$
\frac { \partial J _ { i } } { \partial w _ { p , q , k , k ^ { \prime } } ^ { l } } = \sum _ { m , n } \frac { \partial J _ { i } } { \partial a _ { m , n , k ^ { \prime } } } \frac { \partial a _ { m , n , k ^ { \prime } } ^ { l } } { \partial w _ { p , q , k , k ^ { \prime } } ^ { l } }
$
ここで一度それぞれ、かけられているものを見ると、順伝播の計算から以下のことがすぐに導かれます。
$
\frac { \partial a _ { m , n , k ^ { \prime } } ^ { l } } { \partial w _ { p , q , k , k ^ { \prime } } ^ { l } } = z _ { m + p , n + q , k } ^ { l - 1 }
$
そして問題となってくるのが、$\frac { \partial J _ { i } } { \partial a _ { m , n , k ^ { \prime } } }$の部分ですが、今これを、$\frac { \partial J _ { i } } { \partial a _ { m , n , k ^ { \prime } } ^ { l } } = \delta _ { m , n , k ^ { \prime } } ^ { l }$として表します。$\delta _ { m , n , k ^ { \prime } } ^ { l }$を使ってに表すと、以下のようになります。
$
\frac { \partial J _ { i } } { \partial w _ { p , q , k , k ^ { \prime } } ^ { l } } = \sum _ { m , n } \delta _ { m , n , k ^ { \prime } } ^ { l } \cdot z _ { m + p , n + q , k } ^ { l - 1 }
$
バイアス項に対しても同じように計算しますが、bに関して偏微分したものは1になるので、以下のように表せます。
$
\frac { \partial J _ { i } } { \partial b _ { k ^ { \prime } } ^ { l } } = \sum _ { m , n } \delta _ { m , n , k ^ { \prime } } ^ { l }
$
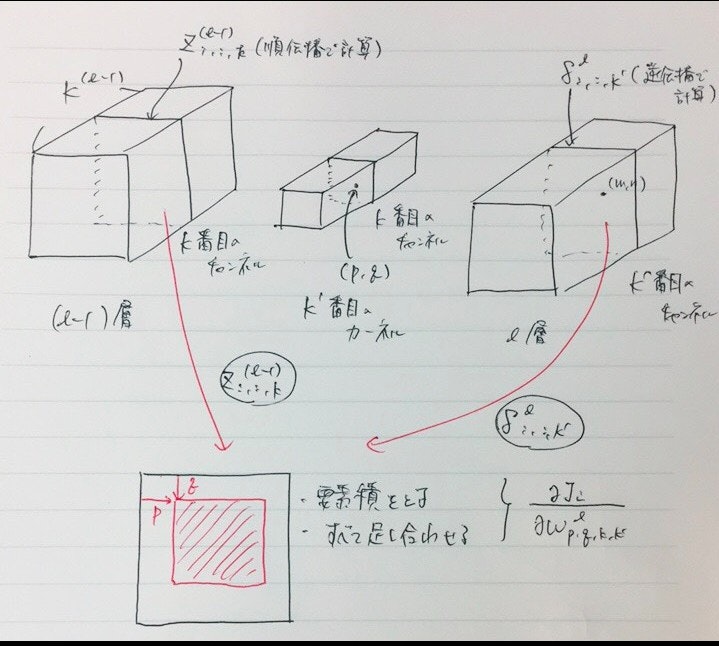
つまり、$\delta _ { m , n , k ^ { \prime } } ^ { l }$が計算することができれば、重みの更新を行うことができます。ちなみに重み更新の際の計算の動きは以下のようになります。下記の図はk'番目のカーネルのkチャンネル目の(p,q)を更新することを想定したものです。使用する箇所は、順伝播で(l-1)層のkチャンネルで計算された出力と、l層のk'チャンネルまでに計算された$\delta^l$を元に計算しています。わかりにくいですが、図の赤い正方形は、$\delta^l_{:,:,k'}$(l層に帰ったきた誤差のうちk'番目のもの)です。(手書きなのは、力尽きました。許してください…)
では、実際に$\delta _ { m , n , k ^ { \prime } } ^ { l }$の逆伝播の様子についてまとめます。$\delta _ { m , n , k ^ { \prime } } ^ { l }$も連鎖律を用いて表すと以下のようになります。
$
\delta _ { m , n , k } ^ { l } = \frac { \partial J _ { i } } { \partial a _ { m , n , k } ^ { l } } = \sum _ { p , q , k ^ { \prime } } \frac { \partial J _ { i } } { \partial a _ { m - p , n - q , k ^ { \prime } } ^ { l + 1 } } \frac { \partial a _ { m - p , n - q , k ^ { \prime } } ^ { l + 1 } } { \partial a _ { m , n , k } ^ { l } }
$
$\frac { \partial a _ { m - p , n - q , k ^ { \prime } } ^ { l + 1 } } { \partial a _ { m , n , k } ^ { l } }$の計算は、順伝播の時の計算を参照すると、以下のようになります。
$
\frac { \partial a _ { m - p , n - q , k ^ { \prime } } ^ { l + 1 } } { \partial a _ { m , n , k } ^ { l } } = w _ { p , q , k , k ^ { \prime } } ^ { l + 1 } h ^ { \prime } \left( a _ { m , n , k } ^ { l } \right)
$
さらに、$\frac { \partial J _ { i } } { \partial a _ { m - p , n - q , k ^ { \prime } } ^ { l + 1 } }=\delta _ { m - p , n - q , k ^ { \prime } } ^ { l + 1 }$となることに注意すると、最終的に以下のようになります。
$
\delta _ { m , n , k } ^ { l } = h ^ { \prime } ( a _ { m , n , k } ^ { l } )\sum _ { p , q , k ^ { \prime } } \delta _ { m - p , n - q , k ^ { \prime } } ^ { l + 1 } \cdot w _ { p , q , k , k ^ { \prime } } ^ { l + 1 }
$
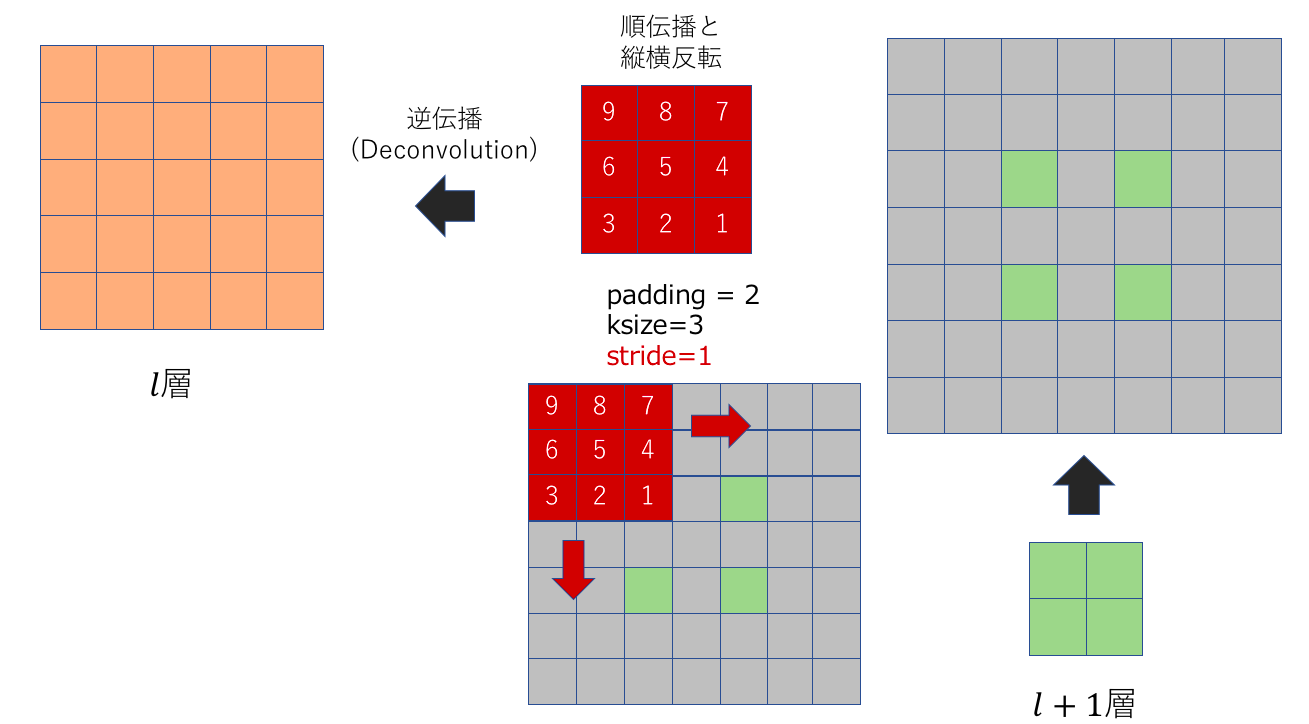
この数式が意味していることは、各辺の外側に(kernel_size -1)の大きさでpaddingをして、重み行列を縦横反転させたのち(わざわざ対象にするピクセルを(m - p)や(n - q)にしている理由に該当)に、特徴マップ上に帰ってきた勾配に対して、重み行列を縦横反転させたのちに畳み込みの計算をしていることと同じになります。(畳み込み処理をしようとして、特徴マップからはみ出た部分は0として扱うみたいなイメージです。)
もちろん数式的に表しているものとしては、重み行列を反転させていないのですが、畳み込み計算を行う$\delta^{l}$の領域に対して、今まで左上の端から順に畳み込み計算を行なっていた部分を、右下の端から計算するように変えているので、結果的に重み行列の縦横を反転させて畳み込みの計算をしたことと同じになります。
2.③サイズを調整するためにzero-paddingや特徴マップへのdilateなどを駆使する
すでに計算でも紹介したように順伝播の時のstrideやpaddingが直接影響してきます。
具体的には、A guide to convolution arithmetic for deep learningこの資料を読んでいただければDeconvolution(Transposed Convolution)に関して自分の得たい情報がすぐに手に入ると思います。ちなみに基本的には、Deconvolutionの出力サイズは、
出力サイズ = stride数 * (inputのサイズ - 1) + カーネルのサイズ - 2*パディング数
で計算されているみたいです。
strideが2以上であった場合の計算もよくわからなかったのですが(と言いますか、これの計算にはめぼしい資料がなかったため)、一応まとめました。気になる人は、下記の注意の部分を参照していただければと思います。後ろの方にchainerの挙動を載せておきました。
※※※※※※※注意※※※※※※※
※の中はchainerの実装コードを読んでも理解できなかったので、もしかしたらあっているかもしれませんし、間違っているかもしれません。(一応chainerでの動作確認はしましたが…)
おそらく順伝播の際のstrideやpaddingの影響は誤差逆伝播やDeconvolutionの時に以下のようになっています。
stride数を元に「stride-1」だけdilateする。paddingとksizeを元に「ksize-padding(順伝播の際にしようしたもの)-1」の大きさでzero-paddingする。畳み込みの際は、重み行列を縦横反転させて、stride数は1に強制する(ここがあっているか不安です)。
ここで一度具体的な例を元に考えてみます。下記のような順伝播を考えます。
5×5の特徴マップから2×2の特徴マップを作成する。(padding=0, stride=2, ksize=3, diliate=1)
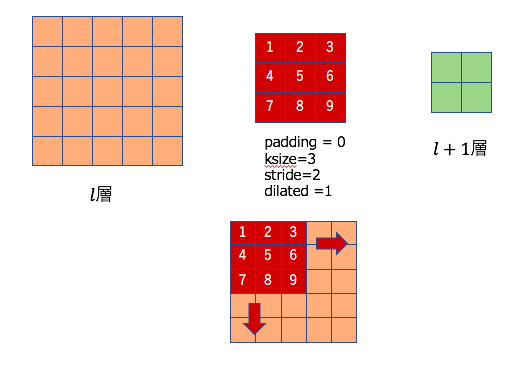
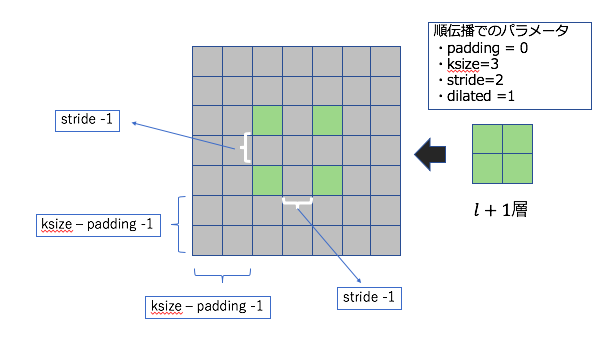
次に考えるものは、上の図で右側(l+1)層に帰ってくる勾配情報を元にl層へ逆伝播する計算過程です。上にも述べましたが、下記のように順伝播の際にしようしたパラメータ(stride数など)を元にzero-paddingを行います。
図は順伝播の時にpadding=0なので、ksize-1の大きさだけ周囲をzero-paddingしています(灰色部分)。次にstride-1だけ特徴マップのピクセルとピクセルの間にzeroを入れてきます。
つまり特徴マップを右の特徴マップの用意リサイズするためのパラメータは以下のようになっていると考えられました。つまり、Deconvolutionで言う所のstride数は、特徴マップをどれくらいdiliateするかという値ということです。
なぜこのように注意喚起をしているかと言いますと、このように考えると辻褄が会うのですが、chainerの実装からそれを読み取ることができなかったからです(誰か強い人確認お願いします…)。一応chainerで簡単な実験をしてみて動作確認をやってあっていたのですが(補足を載せておくのでそちらを参照してください)、厳密にあっているのかわからなかったのであくまで参考にどうぞ…
※※※※※※※注意終了※※※※※※※
3.どのようにして、特徴マップのチャンネル数の違いを合わせているのか?
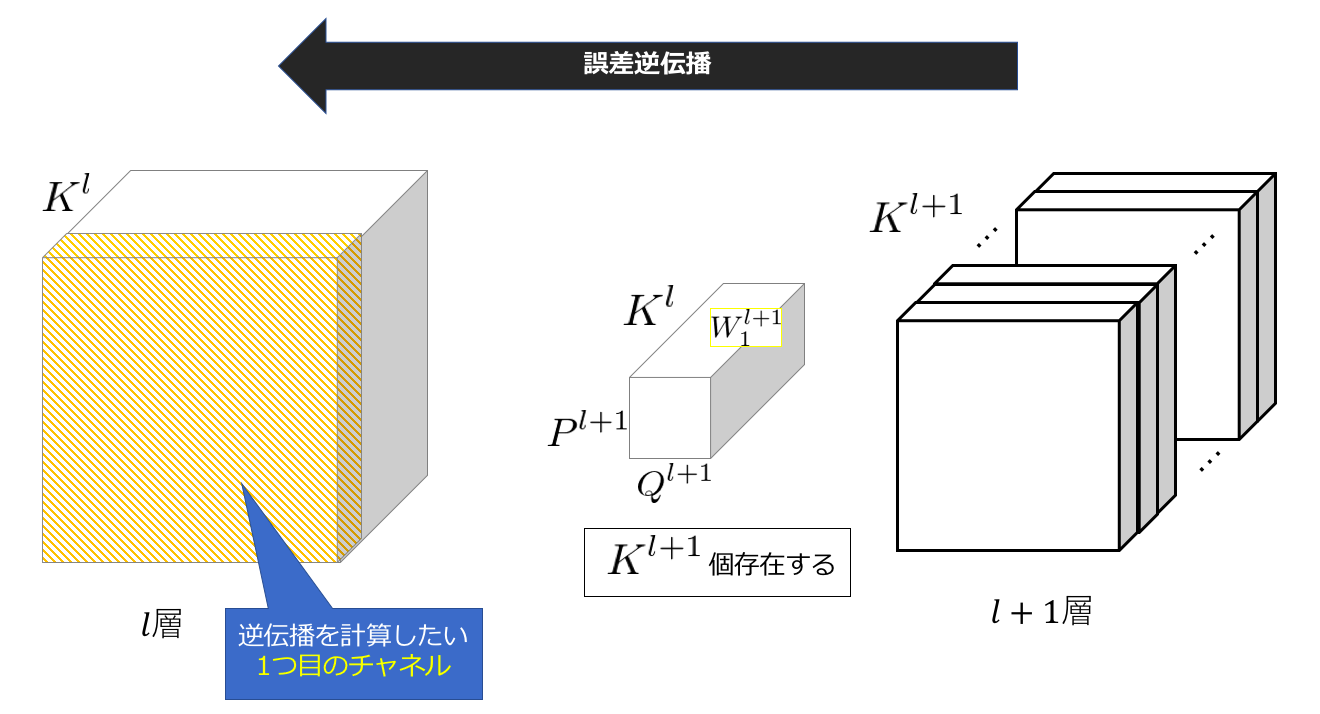
今私がやろうとしていることを図に表すと以下のようになります。
また「2.② 1チャンネルごとに計算を行う」に関して説明をしている際にも登場した際の数式を再掲すると以下のようになります。
$
\delta _ { m , n , k } ^ { l } = h ^ { \prime } ( a _ { m , n , k } ^ { l } )\sum _ { p , q , k ^ { \prime } } \delta _ { m - p , n - q , k ^ { \prime } } ^ { l + 1 } \cdot w _ { p , q , k , k ^ { \prime } } ^ { l + 1 }
$
ここで注目すべきなことは、$\delta _ { m , n , k } ^ { l }$(l層のkチャンネル目の(m,n)の位置にあるピクセル)を計算するために、和の部分にk(l層のチャンネル数)ではなく、k’((l+1)層のチャンネル数)で足し合わせていることです。しかもの添字に注目すると、kは固定した状態で計算を行なっています。
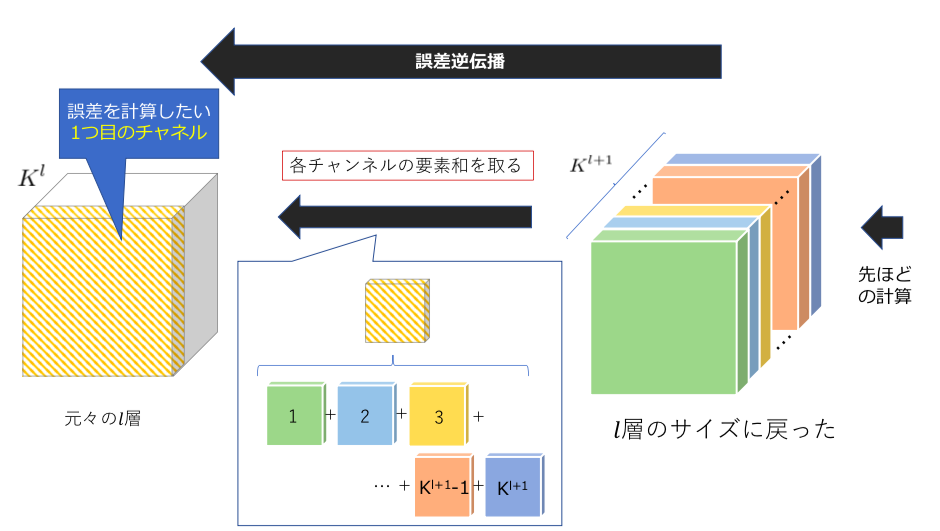
よって上の数式を元に、改めて一度復元したいチャンネル毎の計算過程をおってみたいと思います。画像には記載されていませんが、(l+1)層に帰ってきた勾配テンソルと順伝播で用いたカーネルを使ってl層の1チャネル目に帰ってくるはずの勾配を計算したいというものです。
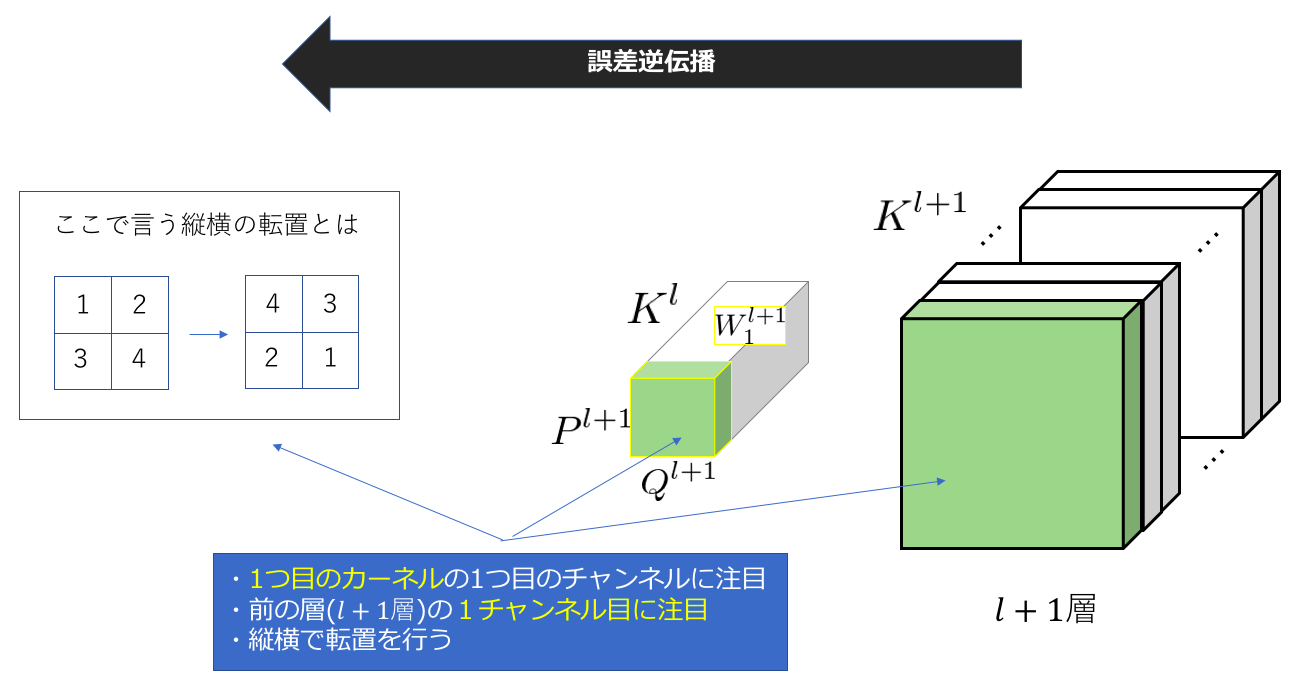
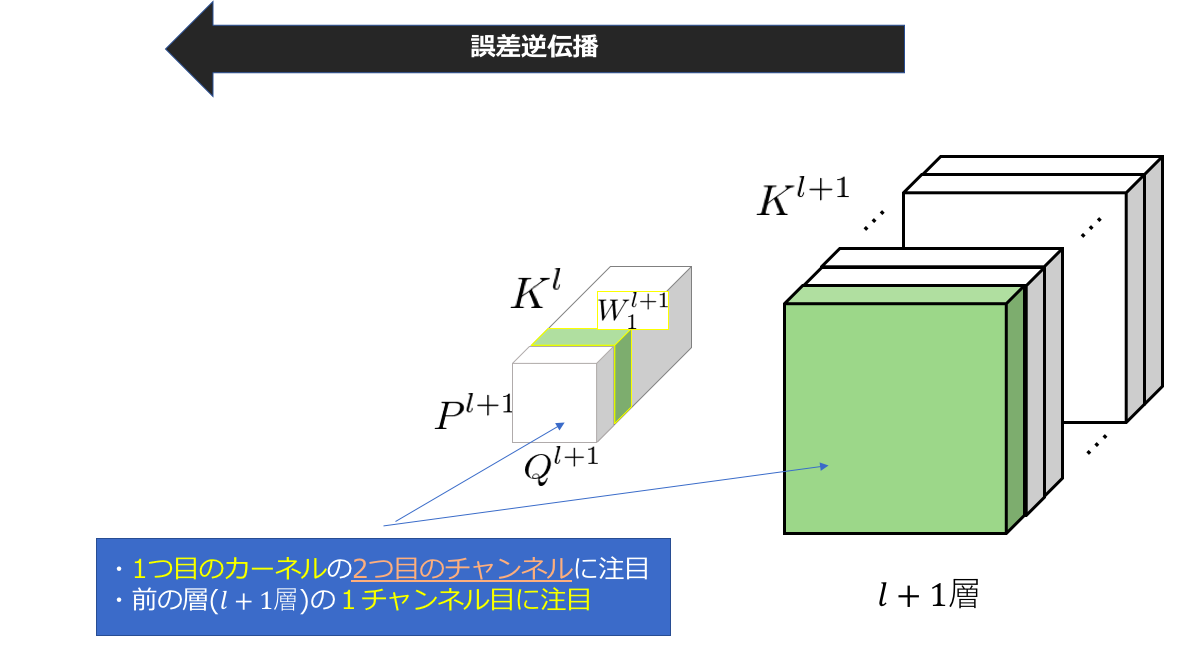
はじめに考える作業は図にも書いてあるように、(l+1)層目の1チャンネル目と1個目のカーネルの1チャンネル目に注目した作業です。つまり、$\delta _ {:,:,1}^{l+1}$と$w_{:,:,k, 1}^{l+1}$に注目します。
先ほどの計算(2.①)でも言ったように、重み行列(重みテンソルの1チャンネル目)を縦横の転置(反転)を行います。
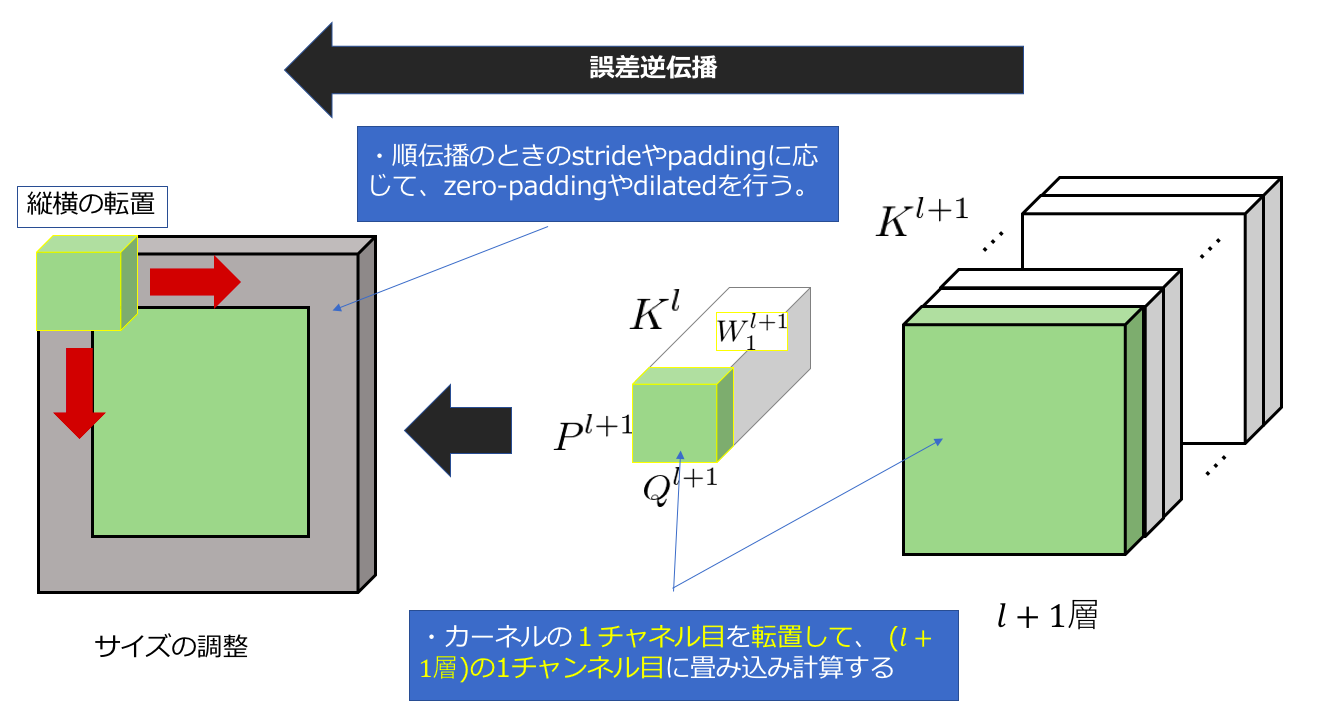
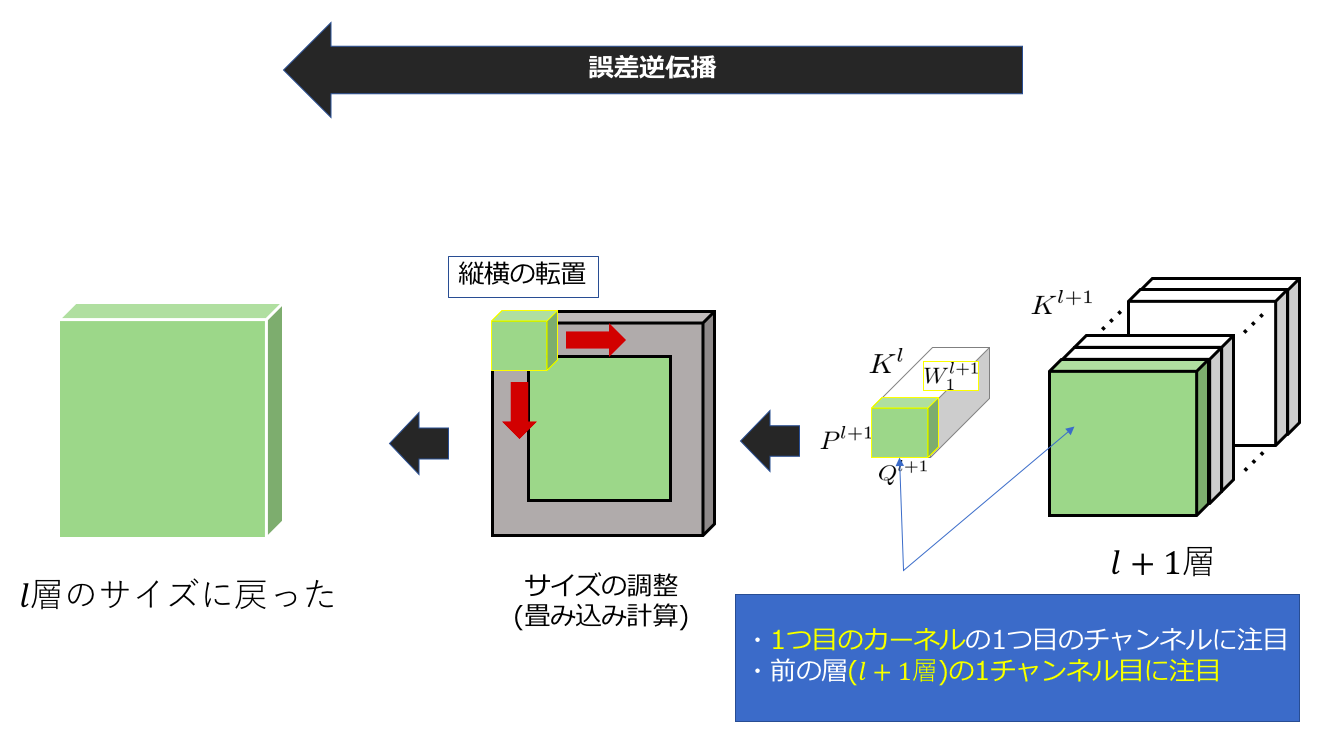
次に、2.③でも触れらたように、zero-paddingや特徴マップへのdilateなどを駆使してサイズを調整します。それが上の図の左側絵になります。そして、このサイズ調整後の特徴マップの勾配に対して、通常の(stride=1 ?)の畳み込み計算を施します。このようにすると、2.①のように、重みが作用した箇所に対して、その重みを用いて逆伝播することができます。ここまでの過程をまとめるとこのようになります。
このようにして、l層の大きさまで、誤差を復元(という言葉が正しいかわかりませんが、逆伝播の方がいいかも?)します。ちなみに2チャンネル目以降の動きは下のslideshareを参考にしてください。(p1~8が参考になると思います)
次に$K^{l+1} $回各チャンネルでこれを繰り返すことで、上の図のカラフルなテンソルが出来上がります。そしてこれを中央の図のようにチャンネル方向に足し合わせることでようやくl層の1チャンネル目に誤差を逆伝播することができました。
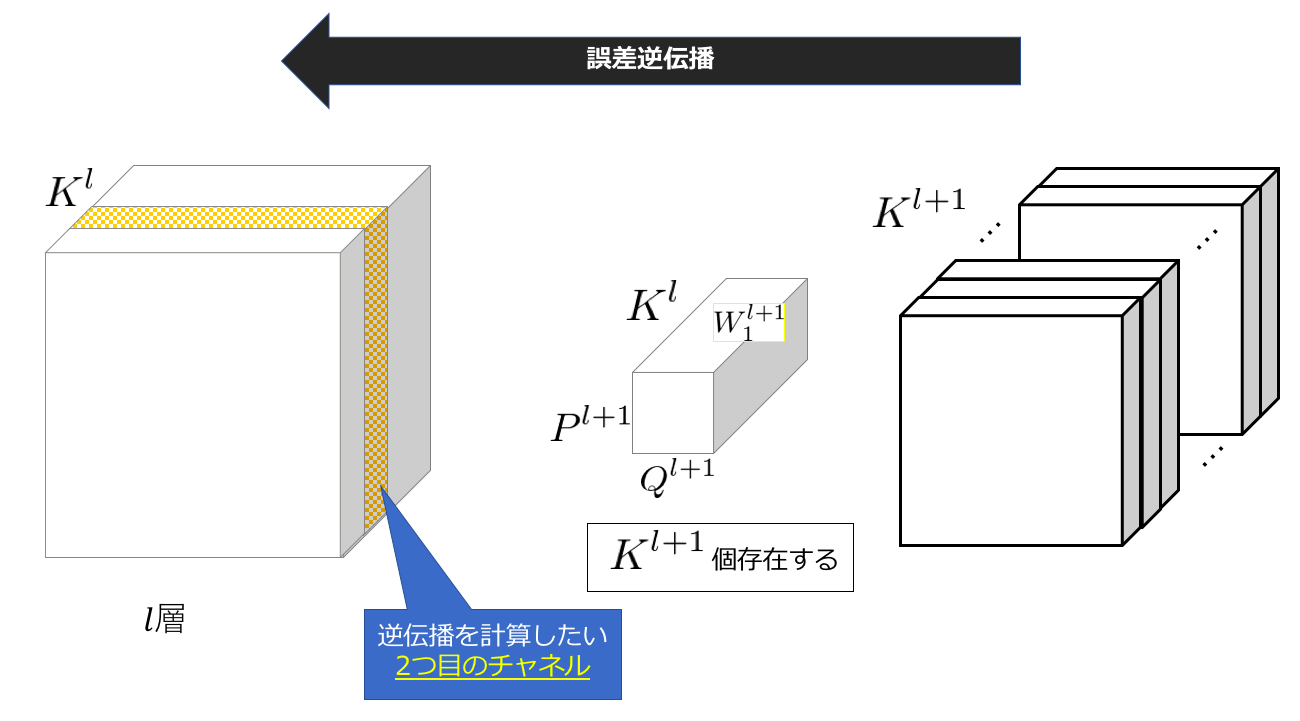
l層の2チャンネル以降の計算は以下のようになります。つまり以下のような計算を行うことを考えます。
今度は、各カーネルの2チャンネル目を用いて同じことを繰り返します。つまり、l層のnチャンネル目の誤差の逆伝播を計算したい場合、各カーネルのn番目のチャンネルを使用するということになります。ちなみにあとは足し合わせるという過程を含めて全て同じです。
詳しい動きは、先ほどあげましたslideに乗っていますので、ご覧いただければと思います。
以上で、CNNの誤差逆伝播の計算過程の説明をおわります。
補足
環境は以下のようになっています。
Python version = 3.6.2
conda version = 4.5.9
chainer.__version__ = 4.3.1
numpy.__version__ = 1.12.1
またモジュールの定義は以下のようになっています。
import chainer
import numpy as np
import chainer.functions as F
import chainer.links as L
from chainer import Variable
chainer での動作確認を行います。
例として、9×9の大きさで要素が全て1となるような入力と、今までの図のように1~9が順番に入っている重みを用意します。(ただしchainerに入れられるようにx.shape=(1,1,9,9),W.shape=(1,1,3,3)としてあります)
[[[[ 1. 1. 1. 1. 1. 1. 1. 1. 1.]
[ 1. 1. 1. 1. 1. 1. 1. 1. 1.]
[ 1. 1. 1. 1. 1. 1. 1. 1. 1.]
[ 1. 1. 1. 1. 1. 1. 1. 1. 1.]
[ 1. 1. 1. 1. 1. 1. 1. 1. 1.]
[ 1. 1. 1. 1. 1. 1. 1. 1. 1.]
[ 1. 1. 1. 1. 1. 1. 1. 1. 1.]
[ 1. 1. 1. 1. 1. 1. 1. 1. 1.]
[ 1. 1. 1. 1. 1. 1. 1. 1. 1.]]]])
[[[[ 1. 2. 3.]
[ 4. 5. 6.]
[ 7. 8. 9.]]]]
以上のパラメータで畳み込み処理を行います。わかりやすいようにsride=3にしてあります。
with chainer.using_config('train', False):
x = Variable(np.ones(9**2).astype("f").reshape(9,9)[None,None,:,:])
W = np.arange(1,10).astype("f").reshape(3,3)[None,None,:,:]
conv = L.Convolution2D(1, 1, ksize=3,stride=3,nobias=True,dilate=1, initialW=W)
conv_output_sum = F.sum(conv(x))
conv.cleargrads()
conv_output_sum.backward(retain_grad=True)
ここでは、詳しい説明は省きたいと思いますが、chainerは出力を逆伝播したいときに、そのまま〇〇.backward()とすると、その値ではなく、勾配が1として計算されるみたいです(conv_outputsum.gradの部分)。ですので、この場合は合計の値が405.0なので、それを逆伝播しているように思われるかもしれませんが、今回δに該当する部分は1となります。
print(conv_output_sum.data)
405.0
print(conv_output_sum.grad)
1.0
print(x.grad)
[[[[ 1. 2. 3. 1. 2. 3. 1. 2. 3.]
[ 4. 5. 6. 4. 5. 6. 4. 5. 6.]
[ 7. 8. 9. 7. 8. 9. 7. 8. 9.]
[ 1. 2. 3. 1. 2. 3. 1. 2. 3.]
[ 4. 5. 6. 4. 5. 6. 4. 5. 6.]
[ 7. 8. 9. 7. 8. 9. 7. 8. 9.]
[ 1. 2. 3. 1. 2. 3. 1. 2. 3.]
[ 4. 5. 6. 4. 5. 6. 4. 5. 6.]
[ 7. 8. 9. 7. 8. 9. 7. 8. 9.]]]]
一応、「※※※※※※※注意※※※※※※※」に記載した通りの動きはしているようです。
次にDeconvolutionの動きを追ってみたいと思います。今度はyという3×3の要素が1の行列を入力として(重みは同じです)、Deconvolutionしたいと思います。先ほどと同様にstride=3です。
[[[[ 1. 1. 1.]
[ 1. 1. 1.]
[ 1. 1. 1.]]]]
with chainer.using_config('train', False):
y = Variable(np.ones(9).astype("f").reshape(3,3)[None,None,:,:])
W = np.arange(1,10).astype("f").reshape(3,3)[None,None,:,:]
deconv = L.Deconvolution2D(1, 1, ksize=3,stride=3,pad=0,nobias=True, initialW=W)
deconv.cleargrads()
deconv_output = deconv(y)
結果を表示すると、1をDeconvolutionした結果と誤差逆伝播が同じ動きをしていることがわかります。
print(deconv_output.data)
array([[[[ 1., 2., 3., 1., 2., 3., 1., 2., 3.],
[ 4., 5., 6., 4., 5., 6., 4., 5., 6.],
[ 7., 8., 9., 7., 8., 9., 7., 8., 9.],
[ 1., 2., 3., 1., 2., 3., 1., 2., 3.],
[ 4., 5., 6., 4., 5., 6., 4., 5., 6.],
[ 7., 8., 9., 7., 8., 9., 7., 8., 9.],
[ 1., 2., 3., 1., 2., 3., 1., 2., 3.],
[ 4., 5., 6., 4., 5., 6., 4., 5., 6.],
[ 7., 8., 9., 7., 8., 9., 7., 8., 9.]]]], dtype=float32)
まとめ
・CNNの逆伝播では、順伝播で使用した重みテンソルを用いるが、その際に縦横の重みは反転させており、各チャンネルごとに計算を行う。
・チャンネル方向の調整は、各カーネルのチャンネルごとに計算を行うことで実現している。
・Convolutionの逆伝播の計算過程で、Deconvolutionを使用している(Chainer限定かも?)
・Stride=2以上の計算は少し不安なので、参考までに…
・Deconvolutionは重みテンソルの縦横を反転させて、色々paddingしたのちに畳み込み処理しただけ(だと思う)。
感想
・今回はなるべく数式と図的なイメージを連結できるように解説をしましたが、正直どこまで正確に把握しているのか自分でもわからないところがあるので、自分で勉強するための参考程度にしていただければと思います。
・絶対にテンソルの計算でうまう具合に処理できるような気がしたが、あくまで今回はイメージが湧くようにすることを優先しました(強がり)
・何かわかりにくいところや、間違えているところがあれば言ってくださればなるべく直すようにするので言ってください。
Reference
・画像認識 (機械学習プロフェッショナルシリーズ)
(この記事の数式部分はほとんど、この書籍を丸ぱくり参考にしました。)
・畳み込みニューラルネットワークにおける順伝播・誤差逆伝播計算
(ネット上に挙げられていて数式が掲載されている資料です。添字は若干異なります。)
・数式で書き下す Convolutional Neural Networks (CNN)
(すごく参考になったブログ記事です。)
・A guide to convolution arithmetic for deep learning
(友人が見つけた論文?資料?です。便利そうだったので、パクりました。)
・Deconvolutional Networks
(Deconvoluionを提案した論文、教師あり学習)
・Visualizing and Understanding Convolution Networks 誤差逆伝播
(Deconvolutionを用いた可視化、教師なし学習、重み行列を縦横に反転すると記載あり)
・Convolution arithmetic
(@taashi さんより紹介されたGithubの資料です。非常にわかりやすいのでこちらではじめに用語の確認とかをするといいかもしれません。)