目次
はじめに
実行環境
接線の交点の座標の求め方
微分係数の求め方
ソースコード
結果
まとめ
はじめに
様々な関数の任意の2点の接線の交点を求めると面白そうだったので、2つの接線の交点のx座標とy座標の式を求めました。
また、Pythonのライブラリである matplotlib を用いて関数のグラフ、任意の2点を通る2つの接線、2つの接線の交点を描画しました。
よろしければこちらもどうぞ!!
実行環境
実行環境は次の通りです。
実行環境
-
実行環境
Windows 10Python 3.10.5
-
ライブラリ
matplotlib 3.6.1
接線の交点の座標の求め方
微分係数を用いた接線の公式は、任意の$x$座標を$a$とし任意の関数を$f(x)$とすると$x$座標のときの$y$座標は$f(a)$と表せます。
また、任意の$x$座標での微分係数を$f'(x)$とし、これを用いると任意の点での接線の傾きを求められ$x=a$での傾きは$f'(a)$と表せます。
これらの値から$x=a$での接線は、以下のように表せます。
y-f(a)=f'(a)(x-a) \label{a}\tag{1}
ここで、新たに任意の$x$座標を$b$とし上記と同様に考えると、接線は以下のように表せます。
y-f(b)=f'(b)(x-b) \label{b}\tag{2}
$(1)-(2)$より、
\begin{align}
f(b)-f(a) & =\Bigl(f'(a)-f'(b)\Bigl)x+f'(b)b-f'(a)a\\
\Bigl(f'(a)-f'(b)\Bigl)x &= f(b)-f(a)-f'(b)b+f'(a)a\\
x&=\frac{f(b)-f(a)-f'(b)b+f'(a)a}{f'(a)-f'(b)} \label{c}\tag{3}
\end{align}
また、$(1)\times f'(b)$より、
f'(b)\times y-f(a)\times f'(b)=f'(a)\times f'(b)\times x-f'(a)\times f'(b)\times a \label{d}\tag{4}
一方で、$(2)\times f'(a)$より、
f'(a)\times y-f'(a)\times f(b)=f'(a)\times f'(b)\times x-f'(a)\times f'(b)\times b \label{e}\tag{5}
$(4)-(5)$より、
\begin{align}
\Bigl(f'(b)-f'(a)\Bigl)y+f'(a)f(b)-f(a)f'(b) & =f'(a)f'(b)b-f'(a)f'(b)a\\
\Bigl(f'(b)-f'(a)\Bigl)y&= (b-a)f'(a)f'(b)-f'(a)f(b)+f(a)f'(b)\\
y&= \frac{(b-a)f'(a)f'(b)-f'(a)f(b)+f(a)f'(b)}{f'(b)-f'(a)}\label{f}\tag{6}
\end{align}
したがって、$(3)$と$(6)$が2つの接線の交点の$x$座標と$y$座標です。
微分係数の求め方
ここで、微分係数の定義式を考えると、
f'(a)=\lim_{h \to 0}\frac{f(a+h)-f(a)}{h} \label{g}\tag{7}
であり、$h$を0に近づけるという極限操作をしなければなりません。しかし、コンピュータ上では極限操作を行うことができません。
そこで、数値微分を行うことで近似的に微分係数を計算しました。
数値微分における3つの差分とその誤差についてを参照すると、
中心差分が最も接線の傾きに近い
らしいので中心差分を用いて微分係数を求めることにしました。ちなみに、中心差分は以下の式で求められるそうです。
f'(x)\approx \frac{f(x+h)-f(x-h)}{2h}
ソースコード
実行環境で示した環境で実行すればおそらく動くはず。
ソースコード
#任意の関数の二接線の交点の座標を算出
#ライブラリのインポート
import numpy as np
import matplotlib.pyplot as plt
#中心差分の式のhを定義
h = 10**(-4)
#aとbを定義
a = -2
b = 2
x = np.linspace(-10,10,1001) #xの値を定義
'''接線の交点を求めたい関数の宣言
本コードでは
y=x^2
とした'''
def func(x):
return x**2
#定義したa,bでの微分係数の計算
dydx_a = (func(a+h)-func(a-h))/(2*h) #x=aでの微分係数
dydx_b = (func(b+h)-func(b-h))/(2*h) #x=bでの微分係数
y_a = dydx_a*x-dydx_a*a+func(a) #x=aでの接線の計算
y_b = dydx_b*x-dydx_b*b+func(b) #x=bでの接線の計算
'''交点のx座標を計算
f(b)-f(a)-f'(b)b+f'(a)a
x_交点 = ----------------------
f'(a)-f'(b)
'''
x_inter = (func(b)-func(a)-dydx_b*b+dydx_a*a)/(dydx_a-dydx_b)
if x_inter == -0.0: #x_interが-0.0になったとき
#(左側極限を考える)
x_inter = 0.0 #x_interを0.0にする
#(-0.0と0.0は、点を考える上では同一と考えてもよいため)
'''交点のy座標を計算
(a-b)f'(a)f'(b)+f'(a)f(b)-f'(b)f(a)
y_交点 = -----------------------------------
f'(a)-f'(b)
'''
y_inter = ((a-b)*dydx_a*dydx_b+dydx_a*func(b)-dydx_b*func(a))/(dydx_a-dydx_b)
#print("f(a) = {:.3f}".format(func(a))) #コメントアウトを外すとx=aでのy座標が出力される
#print("f'(a) = {:.3f}".format(dydx_a)) #コメントアウトを外すとx=aでの微分係数が出力される
#print("f(b) = {:.3f}".format(func(b))) #コメントアウトを外すとx=bでのy座標が出力される
#print("f'(b) = {:.3f}".format(dydx_b)) #コメントアウトを外すとx=bでの微分係数が出力される
#print("x_inter = {:.3f}".format(x_inter)) #コメントアウトを外すと2つの接線の交点のx座標が出力される
#print("y_inter = {:.3f}".format(y_inter)) #コメントアウトを外すと2つの接線の交点のy座標が出力される
#print("(%f,%f)" % (x_inter,y_inter)) #コメントアウトを外すと2つの接線の交点の座標が出力される
plt.xlim(-10,10) #x軸の表示範囲を制限
#plt.ylim(0,2) #y軸の表示範囲を制限
plt.plot(x,func(x)) #任意の関数のグラフを描画
plt.plot(x,y_a) #任意の関数のx=aでの接線を描画
plt.plot(x,y_b) #任意の関数のx=bでの接線を描画
plt.scatter(x_inter,y_inter) #2つの接線の交点を描画
#plt.plot(x,np.zeros(len(x))) #コメントアウトを外すとx=0の直線を描画
plt.show()
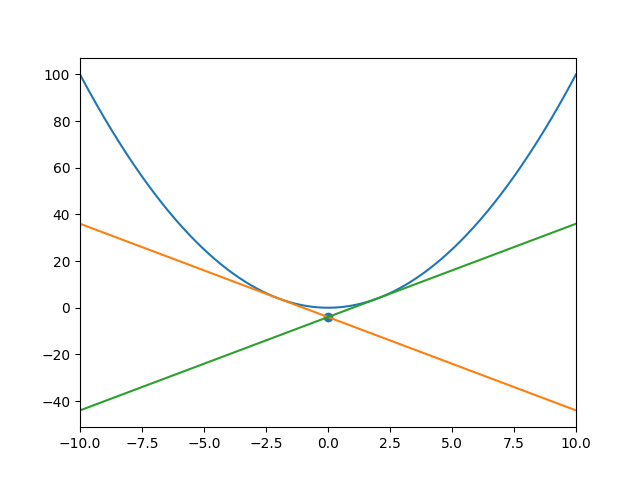
結果
ソースコードを実行した結果は次の通りです。
実行結果のコマンドプロンプト上の表示

上から
- $x=a$での$y$座標である
f(a) - $x=a$での微分係数である
f'(a) - $x=b$での$y$座標である
f(b) - $x=b$での微分係数である
f'(b) - 2つの接線の交点の$x$座標である
x_inter - 2つの接線の交点の$y$座標である
y_inter - 2つの接線の交点の座標(
(x,y)表記)
です。
まとめ
関数の任意の2点の接線の交点の$x$座標と$y$座標を求め、その結果をもとに Python のライブラリであるmatplotlibを用いて接線の交点を描画しました。
この記事をQiitaに投稿するかどうか迷ったが自分のやったことの整理のために有用であると考えたので投稿することにしました。
この記事が実際に役に立つかどうかは分からないですが、誰かの役に立ってくれると嬉しいです。
記事を執筆する余力があれば、次回も記事を投稿する予定です。
次回の予定としては、中心差分を用いて画像の画素ごとの微分を行ってその結果を Pythonのライブラリである OpenCV を用いて表示させたのでそれに関する記事を投稿する予定です。