現在, 会社の有志を集めゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装を用いてDeepLearningの勉強会を行っています.
評判通り, この本には数式とイメージが程よいバランスで記述されており, ストレスなく学ぶことができています.
しかし一方で, 少し行間があったり理由 (もしくは証明) が書かれていない箇所も含まれています.
例えば, 4.3節「数値微分」に次のような記述があります.
(前略) 数値微分には誤差が含まれます。この誤差を減らす工夫として、(x + h) と (x - h) での関数 f の差分を計算することで、誤差を減らすことができます。
何故この工夫で誤差を減らすことができるのか証明はおろか説明もされていなかったため, 自身で調査を行いました.
その結果をここに記します.
ただし, 私は工学出身ではないため厳密でない箇所があるかもしれません. その場合はご指摘をお願いします.
そもそも数値微分って?
関数 $f : \mathbb{R} \rightarrow \mathbb{R}$ に対して, ある点 $x \in \mathbb{R}$ における微分係数 (以下, 単に微分と呼ぶこともある) は以下で定義されます.
$$
f'(x) = \lim_{h \rightarrow0} \dfrac{f(x + h) - f(x)}{h}
$$
高校数学でも習う定義なのでご存じの方も多いと思います.
微分係数はその点における接線の傾きを意味します.
例えばこの定義に従って, $f(x) = x^2$ の $x = 2$ における微分係数を求めてみましょう.
\begin{align*}
f'(2) &= \lim_{h \rightarrow 0}\dfrac{(2 + h)^2 - 2^2}{h}\\
&= \lim_{h \rightarrow 0} (h + 4)\\
&= 4
\end{align*}
よって, $f'(2) = 4$ と求めることができ, $f(x) = x^2$ の $x = 2$ における接線の傾きは $4$ であることが分かります.
上記で見たように, 我々人類は極限操作を行うことができるので定義通りに微分の計算を実行することができます.
しかしプログラムでは $h \rightarrow 0$ のような極限操作を行うことができません.
そのため, $h$ に十分小さい数をとり差分をとることで微分係数を近似します.
このことを 数値微分 と呼びます(対して普段の数学で行う微分のことを 解析的微分 と呼んだりします).
ここで $h$ は十分小さい数とは言っていますが, あまりにも小さい数を取りすぎると丸め誤差が起きる可能性があるので, ここでは書籍と同じく$h = 10^{-4}$ としておきます.
差分の代表的な取り方には次の3種類があります.
前方差分
微分の定義から愚直に差分をとるなら次のようになるでしょう.
$$
f'(x) \approx \dfrac{f(x + h) - f(x)}{h}
$$
$x$ とその前方の点 $x + h$ との差分を考えていることから, これを 前方差分 と呼びます.
後方差分
$x$ とその後方の点 $x - h$ との差分を考える 後方差分 は以下で定義されます.
$$
f'(x) \approx \dfrac{f(x) - f(x - h)}{h}
$$
中心差分
中心差分 は $x$ が中心に来る $x + h$ と $x - h$ との差分をとることで定義されます.
$$
f'(x) \approx \dfrac{f(x + h) - f(x - h)}{2h}
$$
実験
さて, では前方差分, 後方差分, 中心差分を用いて $f(x) = x^2$ の $x = 2$ における数値微分を求めてみましょう.
h = 1e-4 # h = 0.0001
# 数値微分を行う f(x) = x**2 の定義
def func(x):
return x**2
# 前方差分の定義
def front_numerical_diff(f, x):
return (f(x + h) - f(x)) / h
# 後方差分の定義
def back_numerical_diff(f, x):
return (f(x) - f(x - h)) / h
# 中心差分の定義
def center_numerical_diff(f, x):
return (f(x + h) - f(x - h)) / (2 * h)
print('前方差分 :', front_numerical_diff(func, 2))
print('後方差分 :', back_numerical_diff(func, 2))
print('中心差分 :', center_numerical_diff(func, 2))
前方差分 : 4.0001000000078335
後方差分 : 3.999900000000167
中心差分 : 4.000000000004
$f(x) = x^2$ の $x = 2$ における解析的微分の値は $4$ だったので, 確かに書籍の記述通り中心差分の誤差が最も小さいことが分かります.
前方差分, 後方差分, 中心差分を適当なグラフに書いてみると, 接線の傾きに最も近いのは中心差分であることが確認できます(手書きですみません)。
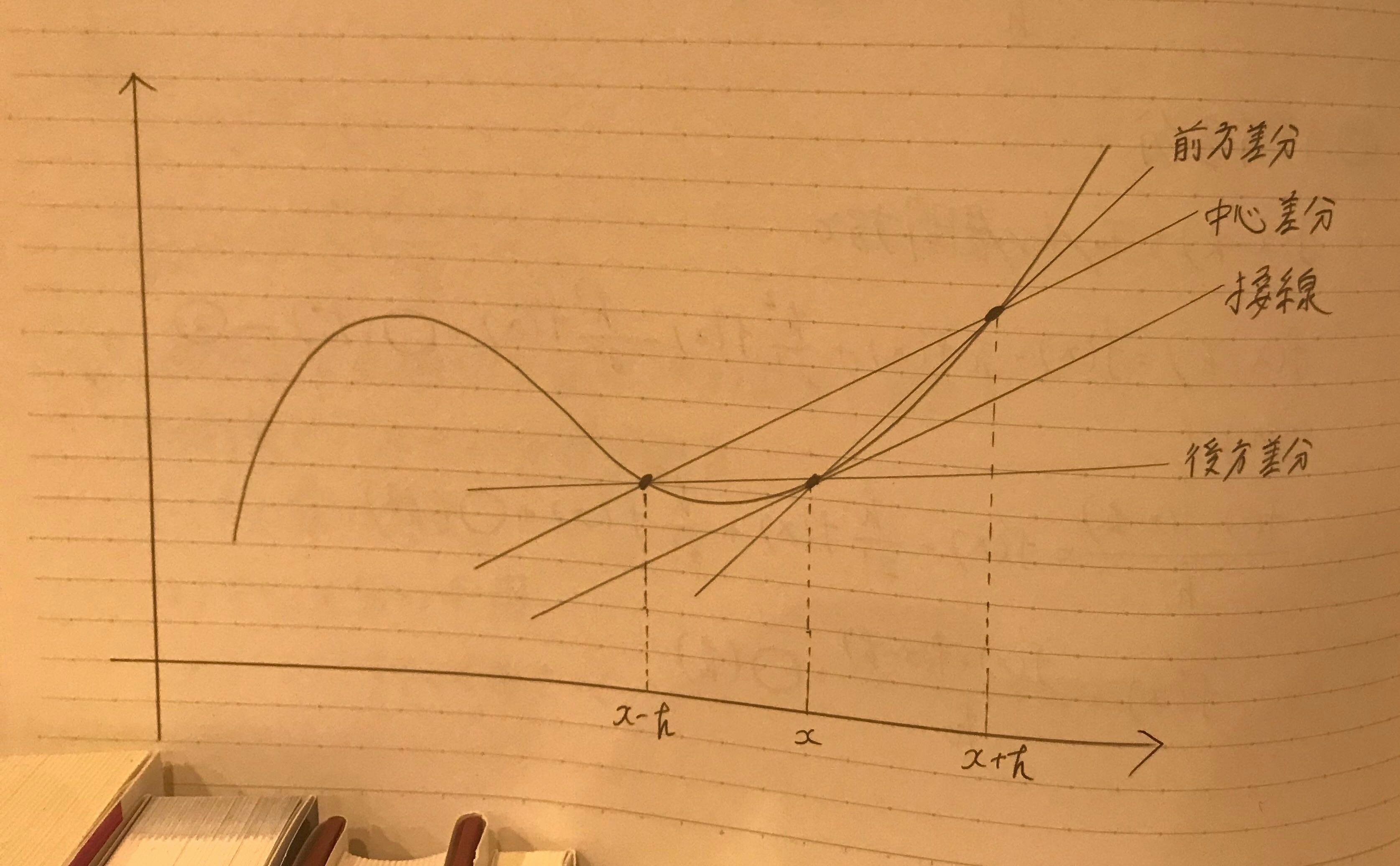
しかしこれは数学的には厳密ではないので, きちんと証明しましょう.
中心差分の誤差が前方差分, 後方差分よりも小さいことの証明
$h$ を十分小さな正の数とし, $f:\mathbb{R} \rightarrow \mathbb{R}$ を微分可能な関数とする.
また, $x \in \mathbb{R}$ をとり固定する.
$f(x + h)$ をTeylor展開すると,
$$
f(x + h) = f(x) + hf'(x) + \frac{h^2}{2!}f''(x) + \frac{h^3}{3!}f'''(x) + O(h^4) \hspace{2cm}(1)
$$
これより,
\begin{align*}
\dfrac{f(x + h) - f(x)}{h} &= f'(x) + \frac{h}{2!}f''(x) + \frac{h^2}{3!}f'''(x) + O(h^3)\\
&= f'(x) + O(h)
\end{align*}
なので,
$$
f'(x) = \dfrac{f(x + h) - f(x)}{h} + O(h)
$$
となって, 前方差分の誤差項は $O(h)$ となる.
次に, $f(x - h)$ をTaylor展開すると,
$$
f(x - h) = f(x) - hf'(x) + \frac{h^2}{2!}f''(x) - \frac{h^3}{3!}f'''(x) + O(h^4) \hspace{2cm}(2)
$$
これより,
\begin{align*}
\dfrac{f(x) - f(x - h)}{h} &= f'(x) - \frac{h}{2!}f''(x) + \frac{h^2}{3!}f'''(x) + O(h^3)\\
&= f'(x) + O(h)
\end{align*}
なので,
$$
f'(x) = \dfrac{f(x) - f(x - h)}{h} + O(h)
$$
となって, 後方差分の誤差項は $O(h)$ となる.
最後に, $(1) - (2)$ より,
$$
f(x + h) - f(x - h) = 2hf'(x) +\frac{2h^3}{3!}f'''(x) + O(h^4)
$$
なので,
\begin{align*}
\dfrac{f(x + h) - f(x - h)}{2h} &= f'(x) + \frac{h^2}{3!}f'''(x) + O(h^3)\\
&=f'(x) + O(h^2)
\end{align*}
であるから,
$$
f'(x) = \dfrac{f(x + h) - f(x - h)}{2h} + O(h^2)
$$
となって, 中心差分の誤差項は $O(h^2)$ となる.
さて, $h$ は十分小さな正の数なので, 誤差項は $O(h)$ よりも $O(h^2)$ の方が小さい.
従って, 中心差分の誤差が最も小さくなる. ■