James-Stein推定量を解説してみた

目的

大学院の授業でJames-Stein推定量という聞き慣れないものを学び、Webで検索したところ、あまり記事が見つからなったので、忘備録として残しておきます。

問題設定

まず、以下の確率モデルを考えます。
$$
p(\boldsymbol{x}|\boldsymbol{\theta})=\prod_{i=1}^D\frac{1}{\sqrt{2\pi}}\exp\left(-\frac{1}{2}(x_i-\theta_i)^2\right),\quad(\boldsymbol{x}\in\mathbb{R}^D,\boldsymbol{\theta}\in\mathbb{R}^D)
$$
これは入力$\boldsymbol{x}$の各次元に独立にガウス分布$\mathcal{N}(\theta_i,1)$を仮定しています。
1個の観測$\boldsymbol{x}$からパラメータ$\boldsymbol{\theta}$を点推定したい。その際、目的関数として設定するのが、
$$
\mathbb{E}_{p(\boldsymbol{x}|\boldsymbol{\theta})}[||\hat{\boldsymbol{\theta}}(\boldsymbol{x})-\boldsymbol{\theta}||^2]\to \mathrm{minimize}
$$
です。つまり、真のパラメータとの平均2乗誤差(Mean Squared Error;MSE)を最小にするようなパラメータを点推定したいという問題設定です。

不偏推定量

平均二乗誤差を最小化する、という問題設定の場合、不偏推定量を採用することが多いです。なぜなら
$$
MSE=\mathbb{V}[\hat{\boldsymbol{\theta}}]+\left(\mathbb{E}[\hat{\boldsymbol{\theta}}]-\boldsymbol{\theta}\right)^2
$$
と推定量の分散とバイアスに分解することができ、不偏推定量は
$$
\mathbb{E}[\hat{\boldsymbol{\theta}}]=\boldsymbol{\theta}
$$
を満たすので、MSEを最小にするには良さそうな推定量に見えるからです。

さて、今回の問題設定の場合だと、
$$
\hat{\boldsymbol{\theta}}_{UB}=\boldsymbol{x}
$$
とすれば、これは不偏推定量となります。そのため、欲しいパラメータの推定量として、これを採用するのは一見良さそうに見えます。

James-Stein推定量とStein's Paradox

ここからがこの記事の本題です。上述したように、不偏推定量はMSEを最小化するような推定量として良さそうに見えると書きましたが、理論的には一番良さそうに見える不偏推定量よりも、MSEをより小さくすることができるのが、James-Stein推定量であり、下式で計算されます。
$$
\hat{\boldsymbol{\theta}}_{JS}=\boldsymbol{x}-\frac{D-2}{||\boldsymbol{x}||^2}\boldsymbol{x}
$$

$D\geq3$の場合、不偏推定量よりもMSEを小さくすることができると知られています(証明略)。

また、「James-Stein推定量を用いることで、不偏推定量よりもMSEが小さくなる」現象のことをSteinのパラドックスと呼びます。

実際に計算してみた

3次元のガウス分布$\mathcal{N}(\boldsymbol{\mu},I)$を用意して、パラメータを以下のように設定します。
$$
\boldsymbol{\mu}=(\mu_1,3,7)^{\top},\quad\mu_1=-20,...,30
$$
なお、共分散行列に単位行列を設定しているので、各次元の独立に正規分布を仮定していることになり、上記の問題設定と同じになります。

$\mu_1$を動かしながら、各パラメータでの正規分布で100,000サンプル生成し、平均二乗誤差を計算してみました。その結果、下図のような結果が得られました。

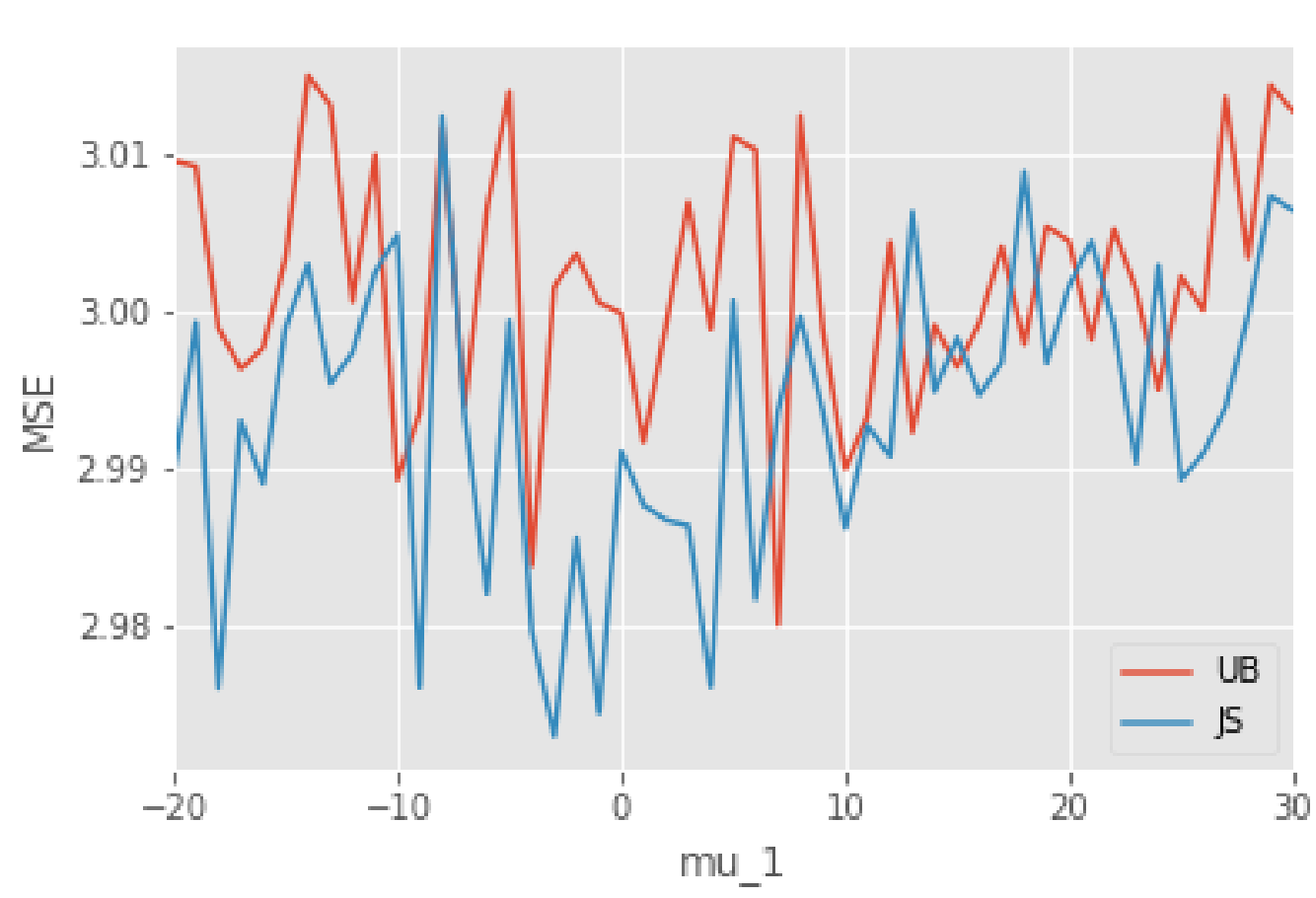
全体的にJames-Stein推定量の方が小さくなっていますね。特に、$\mu_1$が0付近の値だとその特徴が顕著です。しかし、$\mu_1$の絶対値が大きくなってくると、不偏推定量とそこまで変わらないようにも見えます。
おそらく、$\mu_1$の絶対値が大きくなると、James-Stein推定量のノルムが大きい数値になって、不偏推定量の計算とあまり変わらないことが理由だと考察できます。

次に、James-Stein推定量が0付近でのみ、小さくなっている理由を考えるべく、MSEの各次元の寄与をプロットしてみました。

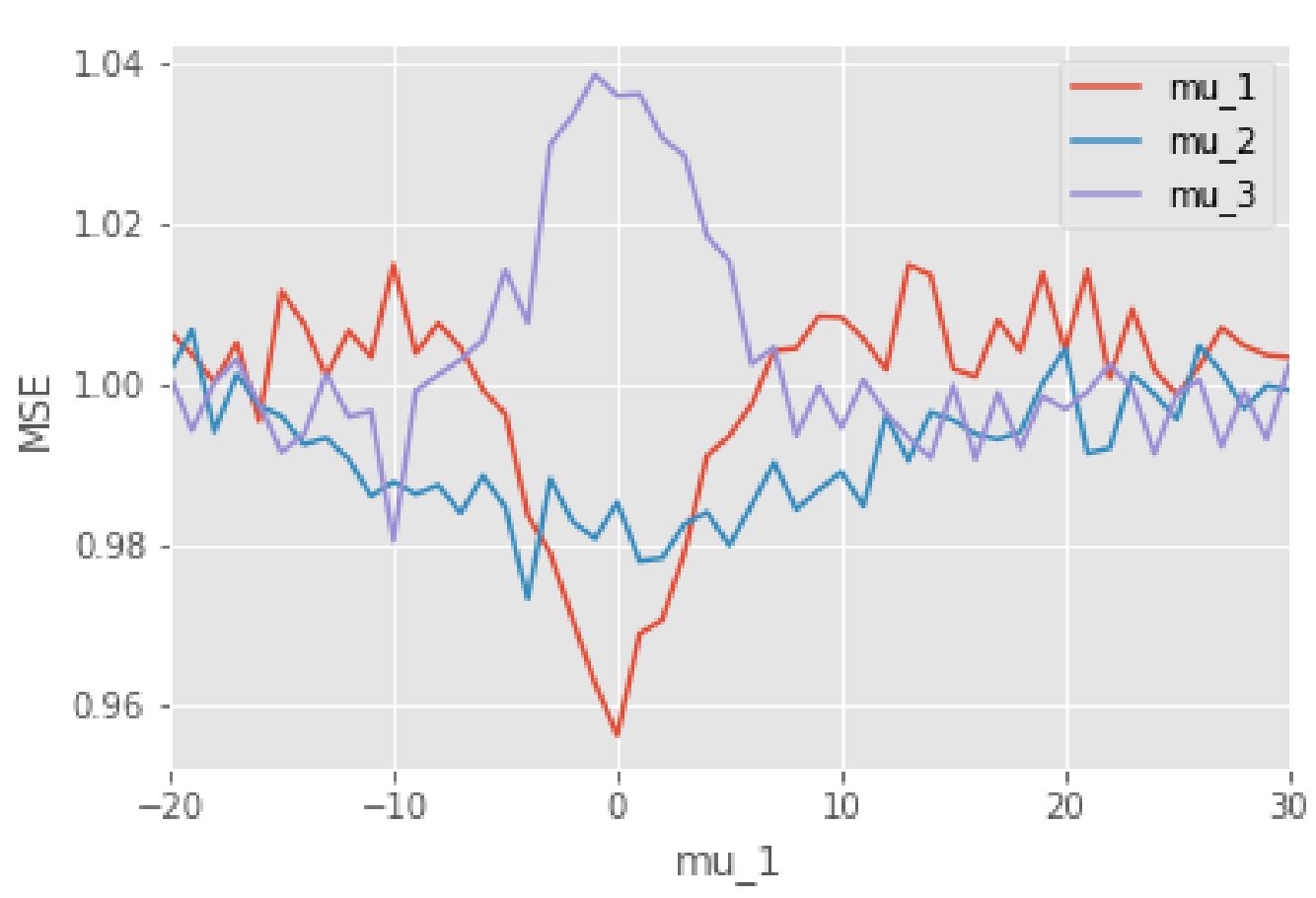
$\mu_1$が0付近で$\mu_1$の寄与が小さく、$\mu_3$の寄与が大きくなっていることが特徴的ですね。しかし、この数値設定だと、互いに相殺しあうように見えるので、先ほどの図で0付近のみMSEが特に小さく見えた理由は、$\mu_2$の寄与が少し小さくなっているからと考えられます。

このようになった理由としては、やはり数値設定が理由にあり、ノルムの値が小さいほど、元のサンプルから引かれる量が大きくなります。$\mu_1=0$の場合だと、大体
$$
1/(3^2+7^2)=0.017
$$
分だけ元のサンプルを減算することになります。パラメータの値が大きい程、線形に減少分が多くなるので、真のパラメータとの解離が大きくなります。そういうわけで、$\mu_3$の寄与が大きくなったのでしょう。

コード

数値実験はPython3.6.9を使って行いました。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
plt.style.use('ggplot')
from tqdm import tqdm

# 実験１
mu1 = np.array(range(-20, 31))
cov = np.eye(3)
NUM_SAMPLE = 100000

ub = []
for mu_1 in tqdm(mu1):
    mu = np.array([mu_1, 4, 7])
    # サンプル生成
    samples = np.random.multivariate_normal(mean=mu, cov=cov, size=NUM_SAMPLE)
    sqr_errors = []
    for sample in samples:
        sqr_error = ((sample - mu)**2).sum()
        sqr_errors.append(sqr_error)
    mse = np.mean(sqr_errors)
    ub.append(mse)

js = []
for mu_1 in tqdm(mu1):
    mu = np.array([mu_1, 4, 7])
    samples = np.random.multivariate_normal(mean=mu, cov=cov, size=NUM_SAMPLE)
    sqr_errors = []
    for sample in samples:
        sample_norm = (sample ** 2).sum()
        sqr_error = ((sample - (1/sample_norm)*sample - mu) ** 2).sum()
        sqr_errors.append(sqr_error)
    mse = np.mean(sqr_errors)
    js.append(mse)

df = pd.DataFrame()
df['ub'] = ub
df['js'] = js
df.index = range(-20, 31)


fig , ax= plt.subplots(1,1)
df['ub'].plot(ax=ax, label='UB')
df['js'].plot(ax=ax, label='JS')
ax.legend()

# 実験2
mu1 = np.array(range(-20, 31))
cov = np.eye(3)
NUM_SAMPLE = 100000

mses = []
for mu_1 in tqdm(mu1):
    mu = [mu_1, 7, 7]
    samples = np.random.multivariate_normal(mean=mu, cov=cov, size=NUM_SAMPLE)
    dim_mse = []
    for sample in samples:
        sample_norm = (sample ** 2).sum()
        sqr_error = ((sample - (1/sample_norm)*sample - mu) ** 2)
        dim_mse.append(sqr_error)
    dim_mse = np.array(dim_mse)
    mses.append(dim_mse.mean(axis=0))

df2 = pd.DataFrame(mses)
df2.index = range(-20, 31)
df2.columns = ['mu_1', 'mu_2', 'mu_3']

fig2, ax2 = plt.subplots(1, 1)
df2['mu_1'].plot(ax=ax2, label='mu_1')
df2['mu_2'].plot(ax=ax2, label='mu_2')
df2['mu_3'].plot(ax=ax2, label='mu_3')
ax2.legend()
ax2.set_xlabel('mu_1')
ax2.set_ylabel('MSE')

まとめ

• 入力の各次元に独立に分布を仮定できる場合に、James-Stein推定量を使うことで、不偏推定量よりもMSEを小さくすることができる
• Steinのパラドックスはパラメータの大きさによっては効果が異なる

これを実際に使って、何かを分析するということをあまりないかもしれませんが、統計学/機械学習の雑学的な知識として、知ってても良いかなと思いました。

以上、暇な土曜日の忘備録投稿でした。