AtCoder Beginner Contest 412
ABの2完(12分0ペナ)でした。
420perfでレートは1108->1054(-54)となりました。
諸事情あり、全く集中できずCとDを落としてしまいました。
今回はA〜Eをまとめます。
A - Task Failed Successfully
$A$が目標の完了数、$B$が実際の完了数を表します。
$A_i<B_i$となるような$i$の個数を求めましょう。
function Main(input) {
input = input.split("\n").map((line) => line.trim());
const N = Number(input[0]);
const [A, B] = [[], []];
for (let i = 0; i < N; i++) [A[i], B[i]] = input[i + 1].split(" ").map(Number);
let ans = 0;
for (let i = 0; i < N; i++) {
if (A[i] < B[i]) ans++;
}
console.log(ans);
}
Main(require("fs").readFileSync(0, "utf8"));
B - Precondition
$S_i (2 \leq i \leq N)$を確認し、$S_i$が英大文字ならば$S_{i-1}$が$T$に含まれるかどうかを確認します。
本番では色々と酷い誤読をしまして、最終的に$S$のうち最初に出てきた大文字以外が$T$に含まれるかを調べるコードを書いたらACしました。
しかしこれは$S=$aBcDe、$T=$cなどでWAです。テストケースが弱く助かりました。
// 嘘解法(初めて出てきた大文字を無視するのかと思っていた)
function Main(input) {
input = input.split("\n").map((line) => line.trim());
const S = input[0];
const T = input[1];
let c = [];
let f = false;
for (let i = 0; i < S.length; i++) {
if (S[i].charCodeAt(0) <= "Z".charCodeAt(0)) {
if (!f) f = true;
else c.push(S[i - 1]);
}
}
for (let i = 0; i < c.length; i++) {
if (!T.includes(c[i])) return console.log("No");
}
console.log("Yes");
}
Main(require("fs").readFileSync(0, "utf8"));
正解は、シンプルに$i=2 \cdots N$の全探索で問題ありません。
// 真の正解
function Main(input) {
input = input.split("\n").map((line) => line.trim());
const S = input[0];
const T = input[1];
for (let i = 1; i < S.length; i++) {
if (S[i].charCodeAt(0) <= "Z".charCodeAt(0)) {
if (!T.includes(S[i - 1])) return console.log("No");
}
}
console.log("Yes");
}
Main(require("fs").readFileSync(0, "utf8"));
C - Giant Domino
もし、ドミノが昇順になっているとします。
このとき、ドミノを並べる最小の手順は、「ドミノ$1$から順に、選べる限界の大きさのドミノを選ぶ」貪欲法で求めることができます。逆に、この手順でドミノ$N$に到達できないのであれば、ドミノ$1$から倒れ最終的にドミノ$N$が倒れるような並べ方はありません。
ドミノ$i$から選べる限界の大きさは、$S_x \le 2S_i$を満たす最大の$x(i \ne x)$を二分探索で求めることによって取得できます。
なお、ドミノ$1$から右へみていくとlowerboundを素直に使えないので、ドミノ$N$から左に見ていくのが良いと思います。
とてもシンプルな問題なので、解法はすぐにわかりました。
しかし、本番では「ドミノ$1$とドミノ$N$はそのままである」という条件に気づかず、全体をソートするという酷い誤読をしてしまいました。
さらに、online-judge-toolsが壊れていて(?)CLIでのデバッグができず、AtCoder Easy Test v2でブラウザ上でのデバッグを試してみても一回のデバッグで30秒以上かかるという最悪の環境でした。何が原因で間違っているのかの究明にあまりにも時間がかかりすぎて、このままでは高い順位が望めないと判断し、次の問題に進みました。
function Main(input) {
input = input.split("\n").map((line) => line.trim());
const T = Number(input[0]);
const ans = new Array(T).fill(-1);
for (let i = 0; i < T; i++) {
const N = Number(input[2 * i + 1]);
const S = input[2 * i + 2].split(" ").map(Number);
const sortedS = S.slice(1, N - 1).sort((a, b) => a - b);
sortedS.unshift(S[0]);
sortedS.push(S[N - 1]);
let cnt = 1;
let min = N - 1;
while (min > 0) {
let idx = lower_bound(sortedS, Math.ceil(sortedS[min] / 2));
if (sortedS[0] * 2 >= sortedS[min]) {
min = 0;
cnt++;
break;
}
if (min == idx) break;
min = idx;
cnt++;
}
if (min > 0) continue;
ans[i] = cnt;
}
console.log(ans.join("\n"));
}
const isOK = (arr, mid, key) => arr[mid] >= key;
const lower_bound = (arr, key) => {
let ng = -1; //「index = 0」が条件を満たすこともあるので、初期値は -1
let ok = arr.length; // 「index = a.size()-1」が条件を満たさないこともあるので、初期値は a.size()
while (ok - ng > 1) {
let mid = Math.floor((ok + ng) / 2);
if (isOK(arr, mid, key)) ok = mid;
else ng = mid;
}
return ok;
};
Main(require("fs").readFileSync(0, "utf8"));
D - Make 2-Regular Graph
$N \le 8$の頂点について、全ての頂点の次数が$2$であるようにするためには辺をちょうど$8$本選ぶ必要があります。したがって、辺を選ぶ組み合わせ数の最大値は$C(28,8) \approx 3 \times 10^6$程度となり、これなら全ての組み合わせを全探索しても十分に間に合います。
実際に、この問題の答えは辺の組み合わせを全探索して、辺の追加・削除コストの最小値を求めるというのは公式解法の一つです。
この解法をすぐに思いつき、計算量的にも問題ないと判断しました。
しかし、実際には別の解法を実装してしまいました。「全ての頂点の次数が$2$であるようなグラフは、全ての頂点が連結された一つのサイクルグラフである」という誤った思い込みがあり、$N$頂点の順列を全探索すればよいと考えたのです。
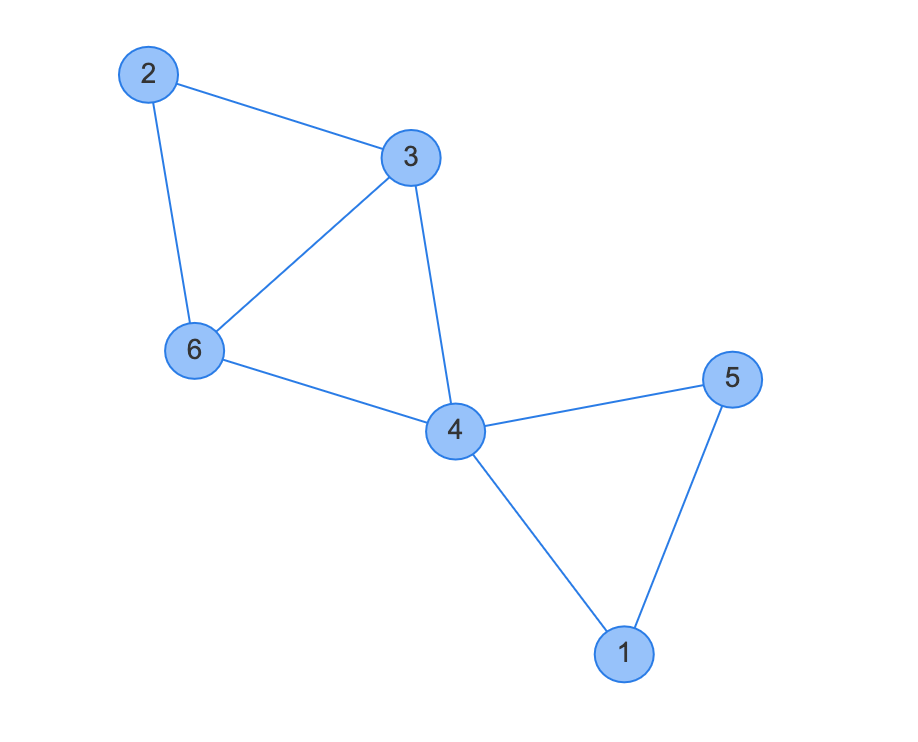
しかし、サンプル3のように、最適解が「全ての頂点が連結された一つのサイクルグラフ」であるとは限りません。この場合、辺3-4と辺4-6を削除するという2回の手順で全ての頂点の次数が$2$となります。
それに気づいたのはコンテスト終了10分前でした。
辺を管理して、デフォルトの辺と照らし合わせるという少しクセのある実装を10分で、デバッグなしでできるはずもなくそのままタイムオーバー。
コンテスト後に以下のdfsを書いてACしました。
function Main(input) {
input = input.split("\n").map((line) => line.trim());
const [N, M] = input[0].split(" ").map(Number);
const [A, B] = [[], []];
const dflt = new Array(N).fill(0).map(() => new Set());
for (let i = 0; i < M; i++) {
[A[i], B[i]] = input[i + 1].split(" ").map(Number);
let [a, b] = [A[i] - 1, B[i] - 1];
if (a > b) [a, b] = [b, a];
dflt[a].add(b);
}
const edges = [];
for (let i = 0; i < N; i++) {
for (let j = i + 1; j < N; j++) {
edges.push([i, j]);
}
}
let min = Infinity;
const visited = new Array(edges.length).fill(false);
let deg = new Array(N).fill(0);
const dfs = (cur, cnt) => {
if (cnt == N) {
let res = 0;
for (let i = 0; i < edges.length; i++) {
let [u, v] = edges[i];
if (visited[i] && !dflt[u].has(v)) res++;
if (!visited[i] && dflt[u].has(v)) res++;
}
min = Math.min(min, res);
return;
}
if (cur == edges.length) return;
let [u, v] = edges[cur];
dfs(cur + 1, cnt);
visited[cur] = true;
deg[u]++;
deg[v]++;
if (deg[u] <= 2 && deg[v] <= 2) dfs(cur + 1, cnt + 1);
deg[u]--;
deg[v]--;
visited[cur] = false;
};
dfs(0, 0);
console.log(min);
}
Main(require("fs").readFileSync(0, "utf8"));
E - LCM Sequence
こちら、コンテスト後にチャレンジして60分程度で解けました。
公式解説よりも少し効率は悪いですが、エラストテネスの篩の知識の延長で解けるということを参考程度に共有します。
区間$[L,R]$に含まれる$A$の種類数を$f$とします。
考察を深めると、$f(L,R)+1=f(L,R+1)$となるような$R+1$の条件は次の二種類であると言えます。
- $x \le R$のすべての$x$について、各素因数の冪乗の最大値を更新する
- $R+1$には、$x \le R$のどの$x$にも含まれていない新たな素因数が存在する(冪乗の最大値が0から1に増えると捉えれば、一つ目の条件と同じ)
例えば、$[L, R]=[4,7]$とします。
このとき、$A=[A_L,.., A_R]=[12, 60, 60, 420]$より$f(4,7)=3$ですが、$[L, R+1]=[4,8]$のとき、$A=[A_L,.., A_R]=[12, 60, 60, 420,840]$より$f(4,8)=4$です。
これは、$4=2^2, 5=5^1, 6=2^ 1\times3^1, 7=7^1, 8=2^3$であり、素因数$2$の冪乗が$8$のときに更新されているから、といえます。
また、$[L, R]=[4,6]$と$[L, R+1]=[4,7]$についても、$f(4,6)=2$、$f(4,7)=3$と$f(L,R)+1=f(L,R+1)$が成り立ちます。
これは、$7$が区間$[4,6]$に登場しない素数$7$を含むからです。
もし、以上の判定法により、$[L, R]$のすべての整数について$f(L,R)+1=f(L,R+1)$となるかどうかを高速に調べることができれば、この問題が解けそうです。
それでは、具体的なアルゴリズムについて考えましょう。
幸い、$R-L\le 10^7$という条件がうまく使えそうです。この条件によって、$10^7$以上の素因数を含む数は、$[L,R]$の範囲に高々一回しか現れないということがわかります。
この条件により、一つ目の条件である「$x \le R$のすべての$x$について、各素因数の冪乗の最大値を更新する」ような数の個数については、$L$から$R$まで順に、$10^7$以下の素数で割れるだけ割って、ある素因数の冪乗の最大値を更新するような数をマークすることによって数え上げることができます。
これを高速に行えるようなアルゴリズムとしては、エラストテネスの篩(素数篩)があります。
区間$[L,R]$において、素数$p$の倍数であるような最小の数$x$を初期値とします。すると、$x, x+ p+,\cdots ,x+p \times k(\le R)$は区間$[L,R]$において素因数$p$をもつような数の全てとなります。この手法により、$M$以下の素因数を持つ数の個数を計算量$O(M \log \log M)$で求めることができます。
今回紹介する回答では、ある素数を素因数に含むかだけではなく、ある素因数の冪乗の最大値を更新するかも見るため、可能な限り割る必要があり、$O(\log R)$だけ余分に計算量が大きくなります。したがって、一つ目の条件を評価するための計算量は$O((R-L)\log \log (R-L) \log R)$です。(ここが公式解説と異なります)
次に、二つ目の条件である、「$x \le R$のどの$x$にも含まれていない新たな素因数が存在する」ような数の個数を求めましょう。
なお、一つ目の条件で区間$[L,R]$の数を$10^7$以下の素数で割れるだけ割った配列を再利用すれば、簡単に求めることができます。
$10^7$以下の素数で割れるだけ割っていて、いまだに$1$よりも大きい値が残っているということは、その数は$10^7$以上の素因数を持っていたということになります。
ここで、$R-L\le 10^7$という条件によって、$10^7$以上の素因数を含む数は、$[L,R]$の範囲に高々一回しか現れないというのを覚えていますか?
そうです、$1$よりも大きい値が残っている要素は、互いに異なる素因数を持ちます。
ただし同時に、$1,2\cdots,L$のLCM(最小公倍数)である$A_L$は、$L$以下の素数を全て含むため、残りは$L$よりも大きい必要があります。
したがって、二つ目の条件を満たすような個数は、$L\le x\le R$中の$x$のうち、$10^7$の素数で割れるだけ割って、なお$L$より大きい数が残っているような数の個数となります。
これは、$O(R-L)$で数え上げることができます。
結果として、一つ目の条件の評価がボトルネックとなり、全体計算量$O((R-L)\log \log (R-L) \log R)$でこの問題をギリギリ解くことができました。
function Main(input) {
input = input.split("\n").map((line) => line.trim());
const [L, R] = input[0].split(" ").map(Number);
const primes = Primetools.sievePrimes(10 ** 7);
const sieves = new Array(R - L + 1).fill(0).map((x, i) => i + L);
let ans = 1;
for (let p of primes) {
if (p > R) break;
let s = Math.ceil(L / p) * p;
let max = 0;
let val = L;
while (val >= p) {
val = Math.floor(val / p);
max++;
}
for (let i = s; i <= R; i += p) {
let cnt = 0;
while (sieves[i - L] % p === 0) {
sieves[i - L] /= p;
cnt++;
}
if (cnt > max) {
max = cnt;
ans++;
}
}
}
for (let i = 0; i < sieves.length; i++) if (sieves[i] > L) ans++;
console.log(ans);
}
以下、Primetoolsライブラリのため割愛
まとめ
C問題のところでも話しましたが、私の環境では数週間前からonline-judge-toolsがコンテスト中の問題で使えなくなってしまい、ブラウザ上でのテストに頼っている現状なのですが、いかんせんコンテスト開始直後だと非常に重く、通常時でも一回のテストに30秒ぐらいかかってしまうため、早解きがやりづらい状況になってしまいました。
そうすると早くサンプルが合っているか確認して提出できなくなるだけでなく、細かい途中経過の確認もしにくくメンタル的にも全く集中できなくなってしまうため、online-judge-toolsが直るまで一旦rated参加は控えようと思います。
ある程度実力不足はあるとは思いますが、不利な状況で参加して積み上げてきたレートが失われたのは残念です。
しばらくはレートにこだわらず、純粋にプログラミングを楽しみたいと思います。