それでは前回記事、魚眼レンズ画像をVRに復元する（前編） ～球体をプロシージャルモデリングする～の続きです。
前回記事では、球面上の任意の座標をユークリッド座標で表すところまでいきました。
ここからは頂点座標配列と、頂点インデックス配列を作っていきます。
DynamicMeshMaker.cs
//縦割りと横割りの単位となる角度
float centerRadianX = 2f * Mathf.PI / (float)divideX; //360°を横分割数で割ったもの
float centerRadianY = Mathf.PI / (float)divideY; //180°を縦分割数で割ったもの
##ステップ1-4 天面の頂点座標配列を求める
天面の頂点座標は球体の一番上にある点なので、座標は(0, r, 0)となります。
半径をr、頂点座標のカウンタ用変数をcnt_vertとしています。
DynamicMeshMaker.cs
//天面の頂点座標
vertices[cnt_vert] = new Vector3(0, r, 0);
cnt_vert++;
##ステップ1-5 側面の頂点座標配列を求める
DynamicMeshMaker.cs
//側面
for (int vy = 0; vy < divideY - 1; vy++) {
//真上から数えた時の角度
float yRadian = (float)(vy + 1) * centerRadianY;
//一辺の長さ
float tmpLen = Mathf.Abs(Mathf.Sin(yRadian));
for (int vx = 0; vx < divideX; vx++) {
Vector3 pos = new Vector3(
tmpLen * Mathf.Sin((float)vx * centerRadianX),
Mathf.Cos(yRadian),
tmpLen * Mathf.Cos((float)vx * centerRadianX)
);
//サイズ反映
vertices[cnt_vert] = pos * r;
cnt_vert++;
}
}
##ステップ1-5 底面の頂点座標配列を求める
底面の頂点座標は球体の一番下にある点なので、座標は(0, -r, 0)となります。
DynamicMeshMaker.cs
//底面の頂点座標
vertices[cnt_vert] = new Vector3(0, -r, 0);
これで頂点座標配列は完成したので、頂点インデックスを作っていきます。
##ステップ1-6 天面、側面、底面の頂点インデックス配列を求める
頂点インデックス配列に関してはこちらの大庭さんの記事がとても詳しいのでこちらを参照していただければと思います。
これで、頂点座標配列と頂点インデックス配列が全て求まりました。
ここまでのコードをすべてまとめるとこんな感じです。
DynamicMeshMaker.cs
using UnityEngine;
[RequireComponent(typeof(MeshFilter))]
[RequireComponent(typeof(MeshRenderer))]
public class DynamicMeshMaker : MonoBehaviour {
private MeshRenderer _renderer;
private MeshRenderer Renderer => _renderer != null ? _renderer : (_renderer = GetComponent<MeshRenderer>());
private MeshFilter _filter;
private MeshFilter Filter => _filter != null ? _filter : (_filter = GetComponent<MeshFilter>());
private Mesh _mesh;
//Materialを保持するようにする
[SerializeField]
private Material _mat;
public Vector2Int divide; //横の分割数、縦の分割数を入れる構造体
public float sphereSize; //球のサイズ
void Update() {
//再生中も変更できるように、毎フレーム更新
Create();
}
[ContextMenu("Create")]
void Create() {
int divideX = divide.x;
int divideY = divide.y;
float size = sphereSize;
MeshData data = CreateSphere(divideX, divideY, sphereSize);
if (_mesh == null) {
_mesh = new Mesh();
}
_mesh.vertices = data.vertices;
_mesh.SetIndices(data.indices, MeshTopology.Triangles, 0);
_mesh.uv = data.uvs;
Filter.mesh = _mesh;
//MeshRendererからMaterialにアクセスし、Materialをセットするようにする
MeshRenderer renderer = GetComponent<MeshRenderer>();
renderer.material = _mat;
_mesh.RecalculateNormals();
}
struct MeshData {
public Vector3[] vertices;
public int[] indices;
public Vector2[] uvs;
}
MeshData CreateSphere(int divideX, int divideY, float size = 1f) {
//分割数は最低でもそれぞれ4にする
divideX = divideX < 4 ? 4 : divideX;
divideY = divideY < 4 ? 4 : divideY;
//
//頂点座標作成
//
//半径
float r = size * 0.5f;
//カウンタ
int cnt_vert = 0;
//頂点の数（天面と底面合わせて）
int vertCount;
vertCount = divideX * (divideY - 1) + 2;
//頂点座標の配列
Vector3[] vertices = new Vector3[vertCount];
//ここで頂点座標を求めていく
//縦割りと横割りの単位となる角度
float centerRadianX = 2f * Mathf.PI / (float)divideX; //360°を横分割数で割ったもの
float centerRadianY = Mathf.PI / (float)divideY; //180°を縦分割数で割ったもの
//天面の頂点座標
vertices[cnt_vert] = new Vector3(0, r, 0);
cnt_vert++;
//側面
for (int vy = 0; vy < divideY - 1; vy++) {
//真上から数えた時の角度
float yRadian = (float)(vy + 1) * centerRadianY;
//一辺の長さ
float tmpLen = Mathf.Abs(Mathf.Sin(yRadian));
for (int vx = 0; vx < divideX; vx++) {
Vector3 pos = new Vector3(
tmpLen * Mathf.Sin((float)vx * centerRadianX),
Mathf.Cos(yRadian),
tmpLen * Mathf.Cos((float)vx * centerRadianX)
);
//サイズ反映
vertices[cnt_vert] = pos * r;
cnt_vert++;
}
}
//底面
vertices[cnt_vert] = new Vector3(0, -r, 0);
//
//頂点インデックス情報
//
//天面と底面の三角形の数
int topAndBottomTriCount;
topAndBottomTriCount = divideX * 2;
//天面と底面以外の三角形の数
int aspectTriCount;
aspectTriCount = divideX * (divideY - 2) * 2;
//頂点インデックスの配列を生成
int[] indices = new int[(topAndBottomTriCount + aspectTriCount) * 3];
//ここで頂点インデックスを求めていく
//天面
int offsetIndex = 0;
cnt_vert = 0;
for (int i = 0; i < divideX * 3; i++) {
if (i % 3 == 0) {
//天面の出っ張り
indices[cnt_vert] = 0;
cnt_vert++;
} else if (i % 3 == 1) {
int index = 2 + offsetIndex;
if (index > divideX) {
index = indices[2];
}
indices[cnt_vert] = index;
cnt_vert++;
} else if (i % 3 == 2) {
indices[cnt_vert] = 1 + offsetIndex;
cnt_vert++;
offsetIndex++;
}
}
//側面
//開始Index番号
int startIndex = indices[2];
//天面と底面以外のIndex要素数
int sideIndexLen = aspectTriCount * 3;
//ループ時に使用するIndex
int loop1stIndex = 0;
int loop2ndIndex = 0;
//ピンクの帯一周分のIndex要素数
int lapDiv = divideX * 2 * 3;
//何本目の帯に取り掛かっているのか（一本目を１とする）
int createSquareFaceCount = 0;
for (int i = 0; i < sideIndexLen; i++) {
//一周の帯を終了したら次の帯に移動する
if (i % lapDiv == 0) {
loop1stIndex = startIndex;
loop2ndIndex = startIndex + divideX;
createSquareFaceCount++;
}
if (i % 6 == 0) {
indices[cnt_vert] = startIndex;
cnt_vert++;
} else if (i % 6 == 1) {
if (i > 0 && i % (lapDiv * createSquareFaceCount - 5) == 0) {
//一周したときのループ処理
indices[cnt_vert] = loop2ndIndex;
cnt_vert++;
} else {
indices[cnt_vert] = startIndex + divideX + 1;
cnt_vert++;
}
} else if (i % 6 == 2) {
indices[cnt_vert] = startIndex + divideX;
cnt_vert++;
} else if (i % 6 == 3) {
indices[cnt_vert] = startIndex;
cnt_vert++;
} else if (i % 6 == 4) {
if (i > 0 && i % (lapDiv * createSquareFaceCount - 2) == 0) {
//一周したときのループ処理
indices[cnt_vert] = loop1stIndex;
cnt_vert++;
} else {
indices[cnt_vert] = startIndex + 1;
cnt_vert++;
}
} else if (i % 6 == 5) {
if (i > 0 && i % (lapDiv * createSquareFaceCount - 1) == 0) {
//一周したときのループ処理
indices[cnt_vert] = loop2ndIndex;
cnt_vert++;
} else {
indices[cnt_vert] = startIndex + divideX + 1;
cnt_vert++;
}
//開始Indexの更新
startIndex++;
}
}
//底面
offsetIndex = vertices.Length - 1 - divideX;
int loopIndex = offsetIndex;
for (int i = 0; i < divideX * 3; i++) {
if (i % 3 == 0) {
//底面の先頂点
indices[cnt_vert] = vertices.Length - 1;
cnt_vert++;
} else if (i % 3 == 1) {
indices[cnt_vert] = offsetIndex;
cnt_vert++;
} else if (i % 3 == 2) {
int value = 1 + offsetIndex;
if (value >= vertices.Length - 1) {
value = loopIndex;
}
indices[cnt_vert] = value;
cnt_vert++;
offsetIndex++;
}
}
return new MeshData() {
vertices = vertices,
indices = indices,
};
}
}
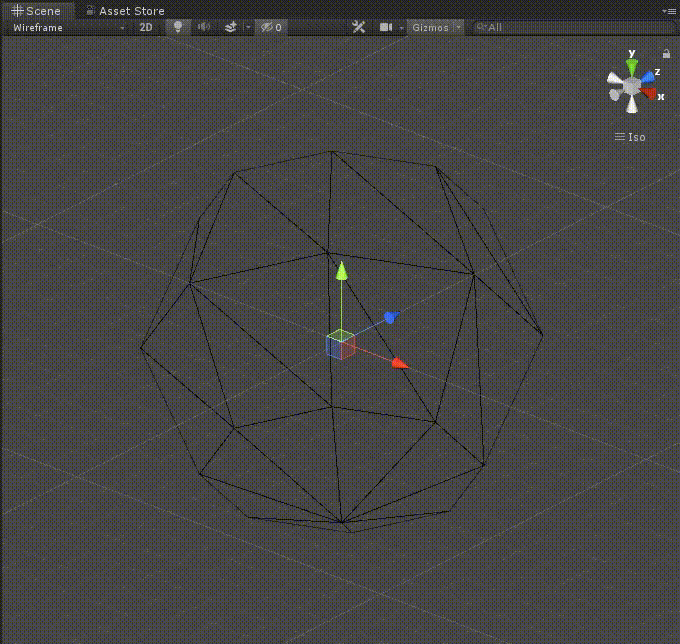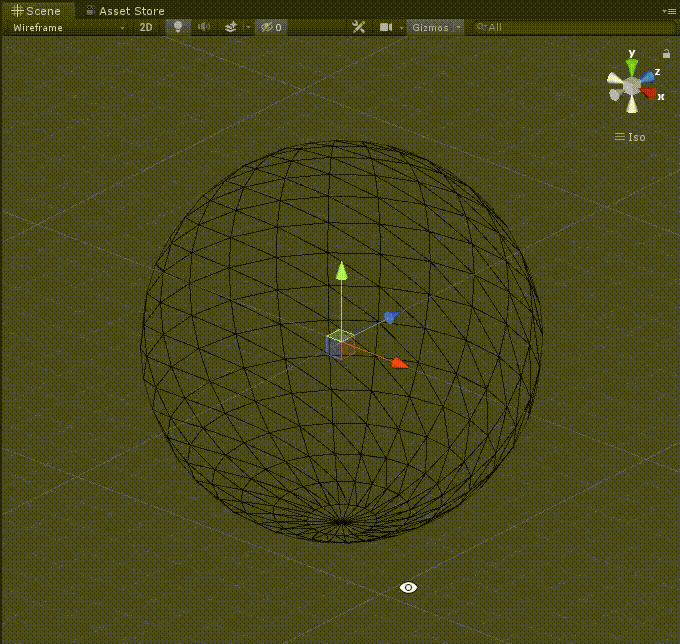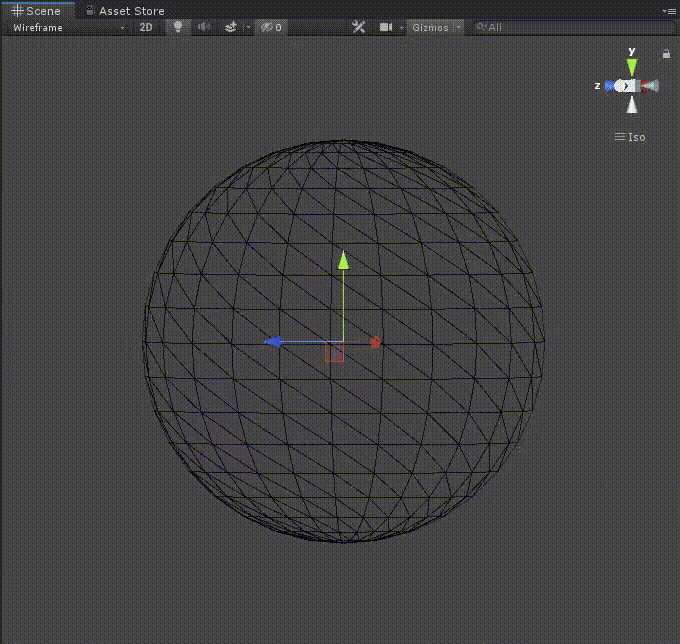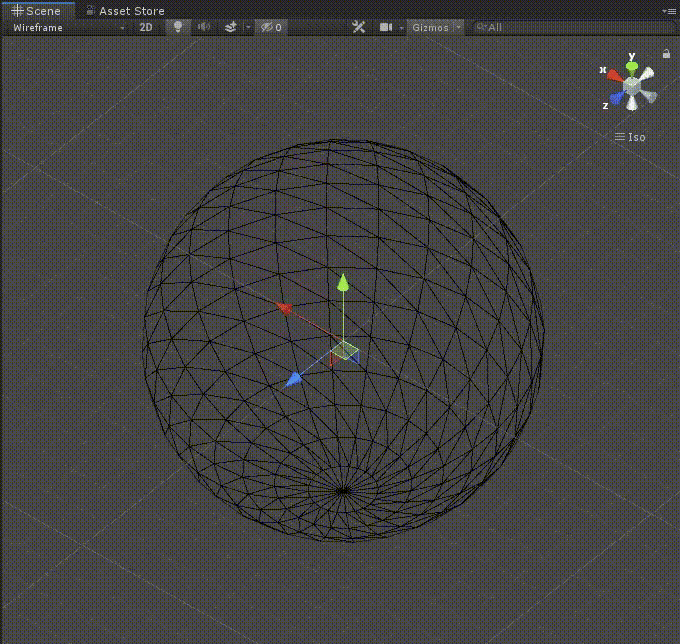
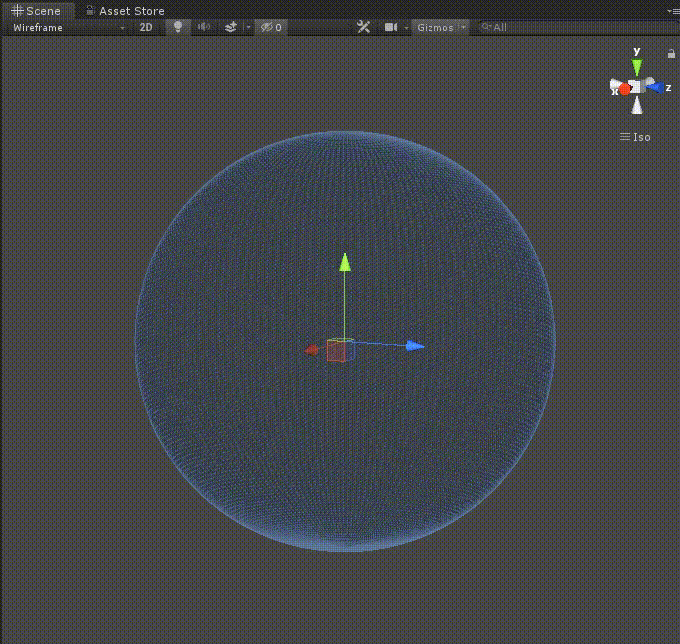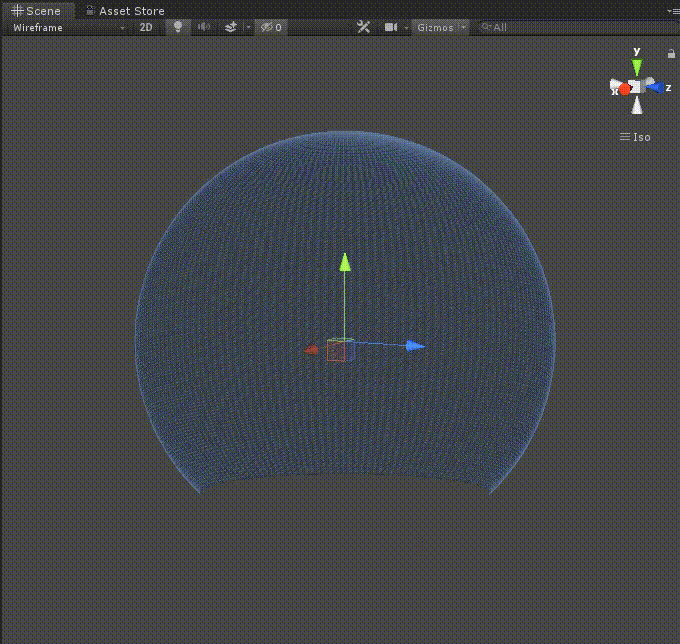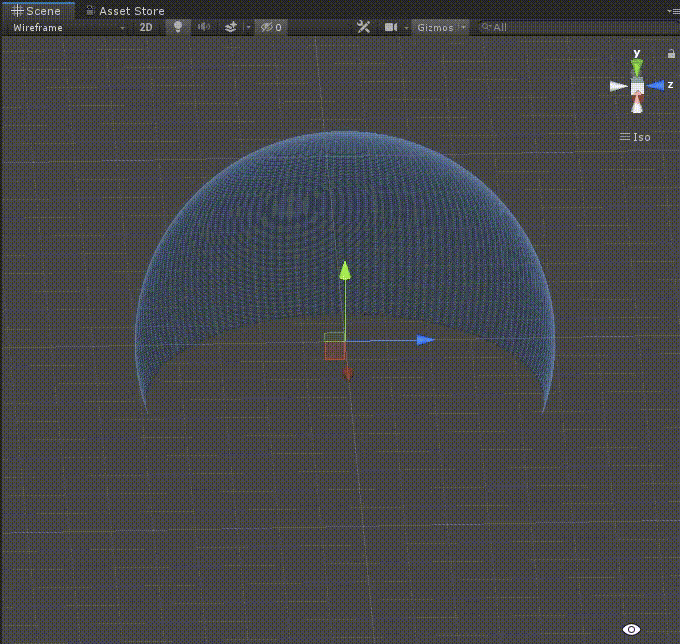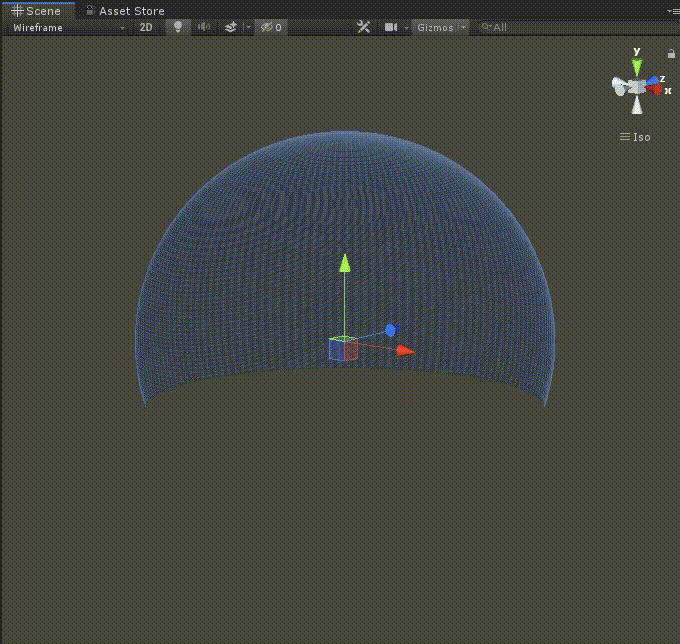
##実行
これで実行してみましょう。
再生して、divide構造体の値やsphereSizeの値を変えてみましょう。
再生しながらメッシュの縦割りと横割りの数を変更出来たら、ひとまず成功です。
（下のgifでは、Materialは未設定のためWireframeで表示しています。）
これでステップ1は終了です！お疲れさまでした。
さて、すかさずステップ2に移りましょう。
#ステップ２：球体を任意の中心角N°で切断したものを作る（N°の切断球と呼ぶ）
ステップ１で作ったものに手を加えていきます。
まずはカメラの視野角にあたる変数を新しく作ります。（これが切断球の中心角Nにあたります。）
DynamicMeshMaker.cs
[Range(0, 360)]
public float fov = 200; //魚眼カメラの視野角
中心角の単位が変わるので、
DynamicMeshMaker.cs
float centerRadianY = (fov / 2) * Mathf.Deg2Rad / (float)divideY; //FOVの半分の値を縦分割数で割ったもの
さらにNが360度未満の時は、頂点のカウントの仕方が変わるので、fovによって頂点数の計算を変えます。
DynamicMeshMaker.cs
//頂点の数（天面と底面合わせて）
int vertCount;
if (fov == 360) {
vertCount = divideX * (divideY - 1) + 2;
} else {
vertCount = divideX * divideY + 1;
}
そして、側面のforループをdivideY - 1 → fovへと変更します。
DynamicMeshMaker.cs
for (int vy = 0; vy < fov; vy++) {
//中身は省略
}
fovが360未満の時、一番最後の頂点座標がカウント漏れしているので、
DynamicMeshMaker.cs
//最後の頂点座標
if (fov != 360) {
vertices[vertCount - 1] = vertices[vertCount - divideX];
}
底面の頂点座標はfov=360のときのみ存在するので、if文で囲います。
DynamicMeshMaker.cs
//底面
if (fov == 360) {
vertices[cnt_vert] = new Vector3(0, -r, 0);
}
次に、頂点インデックスです。
fovが360未満の時、底面の三角形はなくなるため、下記のように書き換えます。
DynamicMeshMaker.cs
//天面と底面の三角形の数
int topAndBottomTriCount;
if (fov == 360) {
topAndBottomTriCount = divideX * 2;
} else {
topAndBottomTriCount = divideX;
}
また、天面と底面以外の三角形の数も以下のように変わります。
DynamicMeshMaker.cs
//天面と底面以外の三角形の数
int aspectTriCount;
if (fov == 360) {
aspectTriCount = divideX * (divideY - 2) * 2;
} else {
aspectTriCount = divideX * (divideY - 1) * 2;
}
最後に、底面の頂点インデックスは、fov=360の時のみ計算されるので、if文でくくります。
DynamicMeshMaker.cs
if (fov == 360) {
offsetIndex = vertices.Length - 1 - divideX;
int loopIndex = offsetIndex;
for (int i = 0; i < divideX * 3; i++) {
if (i % 3 == 0) {
//底面の先頂点
indices[cnt_vert] = vertices.Length - 1;
cnt_vert++;
} else if (i % 3 == 1) {
indices[cnt_vert] = offsetIndex;
cnt_vert++;
} else if (i % 3 == 2) {
int value = 1 + offsetIndex;
if (value >= vertices.Length - 1) {
value = loopIndex;
}
indices[cnt_vert] = value;
cnt_vert++;
offsetIndex++;
}
}
}
さて、これでN度の切断級に対応したバージョンになりました。
ここまでのコードをまとめると、以下のようになります。
DynamicMeshMaker.cs
using UnityEngine;
[RequireComponent(typeof(MeshFilter))]
[RequireComponent(typeof(MeshRenderer))]
public class DynamicMeshMaker : MonoBehaviour {
private MeshRenderer _renderer;
private MeshRenderer Renderer => _renderer != null ? _renderer : (_renderer = GetComponent<MeshRenderer>());
private MeshFilter _filter;
private MeshFilter Filter => _filter != null ? _filter : (_filter = GetComponent<MeshFilter>());
private Mesh _mesh;
[Range(0, 360)]
public float fov = 200; //魚眼カメラの視野角
//Materialを保持するようにする
[SerializeField]
private Material _mat;
public Vector2Int divide; //横の分割数、縦の分割数を入れる構造体
public float sphereSize; //球のサイズ
void Update() {
//再生中も変更できるように、毎フレーム更新
Create();
}
[ContextMenu("Create")]
void Create() {
int divideX = divide.x;
int divideY = divide.y;
float size = sphereSize;
MeshData data = CreateSphere(divideX, divideY, sphereSize);
if (_mesh == null) {
_mesh = new Mesh();
}
_mesh.vertices = data.vertices;
_mesh.SetIndices(data.indices, MeshTopology.Triangles, 0);
_mesh.uv = data.uvs;
Filter.mesh = _mesh;
//MeshRendererからMaterialにアクセスし、Materialをセットするようにする
MeshRenderer renderer = GetComponent<MeshRenderer>();
renderer.material = _mat;
_mesh.RecalculateNormals();
}
struct MeshData {
public Vector3[] vertices;
public int[] indices;
public Vector2[] uvs;
}
MeshData CreateSphere(int divideX, int divideY, float size = 1f) {
//分割数は最低でもそれぞれ4にする
divideX = divideX < 4 ? 4 : divideX;
divideY = divideY < 4 ? 4 : divideY;
//
//頂点座標作成
//
//半径
float r = size * 0.5f;
//カウンタ
int cnt_vert = 0;
//頂点の数（天面と底面合わせて）
int vertCount;
if (fov == 360) {
vertCount = divideX * (divideY - 1) + 2;
} else {
vertCount = divideX * divideY + 1;
}
//頂点座標の配列
Vector3[] vertices = new Vector3[vertCount];
//ここで頂点座標を求めていく
//縦割りと横割りの単位となる角度
float centerRadianX = 2f * Mathf.PI / (float)divideX; //360°を横分割数で割ったもの
float centerRadianY = (fov / 2) * Mathf.Deg2Rad / (float)divideY; //FOVの半分の値を縦分割数で割ったもの
//天面の頂点座標
vertices[cnt_vert] = new Vector3(0, r, 0);
cnt_vert++;
//側面
for (int vy = 0; vy < fov; vy++) {
//真上から数えた時の角度
float yRadian = (float)(vy + 1) * centerRadianY;
//一辺の長さ
float tmpLen = Mathf.Abs(Mathf.Sin(yRadian));
for (int vx = 0; vx < divideX; vx++) {
Vector3 pos = new Vector3(
tmpLen * Mathf.Sin((float)vx * centerRadianX),
Mathf.Cos(yRadian),
tmpLen * Mathf.Cos((float)vx * centerRadianX)
);
//サイズ反映
vertices[cnt_vert] = pos * r;
if (cnt_vert < vertCount - 1) {
cnt_vert++;
}
}
}
//最後の頂点座標
if (fov != 360) {
vertices[vertCount - 1] = vertices[vertCount - divideX];
}
//底面
if (fov == 360) {
vertices[cnt_vert] = new Vector3(0, -r, 0);
}
//
//頂点インデックス情報
//
//天面と底面の三角形の数
int topAndBottomTriCount;
if (fov == 360) {
topAndBottomTriCount = divideX * 2;
} else {
topAndBottomTriCount = divideX;
}
//天面と底面以外の三角形の数
int aspectTriCount;
if (fov == 360) {
aspectTriCount = divideX * (divideY - 2) * 2;
} else {
aspectTriCount = divideX * (divideY - 1) * 2;
}
//頂点インデックスの配列を生成
int[] indices = new int[(topAndBottomTriCount + aspectTriCount) * 3];
//ここで頂点インデックスを求めていく
//天面
int offsetIndex = 0;
cnt_vert = 0;
for (int i = 0; i < divideX * 3; i++) {
if (i % 3 == 0) {
//天面の出っ張り
indices[cnt_vert] = 0;
cnt_vert++;
} else if (i % 3 == 1) {
int index = 2 + offsetIndex;
if (index > divideX) {
index = indices[2];
}
indices[cnt_vert] = index;
cnt_vert++;
} else if (i % 3 == 2) {
indices[cnt_vert] = 1 + offsetIndex;
cnt_vert++;
offsetIndex++;
}
}
//側面
//開始Index番号
int startIndex = indices[2];
//天面と底面以外のIndex要素数
int sideIndexLen = aspectTriCount * 3;
//ループ時に使用するIndex
int loop1stIndex = 0;
int loop2ndIndex = 0;
//ピンクの帯一周分のIndex要素数
int lapDiv = divideX * 2 * 3;
//何本目の帯に取り掛かっているのか（一本目を１とする）
int createSquareFaceCount = 0;
for (int i = 0; i < sideIndexLen; i++) {
//一周の帯を終了したら次の帯に移動する
if (i % lapDiv == 0) {
loop1stIndex = startIndex;
loop2ndIndex = startIndex + divideX;
createSquareFaceCount++;
}
if (i % 6 == 0) {
indices[cnt_vert] = startIndex;
cnt_vert++;
} else if (i % 6 == 1) {
if (i > 0 && i % (lapDiv * createSquareFaceCount - 5) == 0) {
//一周したときのループ処理
indices[cnt_vert] = loop2ndIndex;
cnt_vert++;
} else {
indices[cnt_vert] = startIndex + divideX + 1;
cnt_vert++;
}
} else if (i % 6 == 2) {
indices[cnt_vert] = startIndex + divideX;
cnt_vert++;
} else if (i % 6 == 3) {
indices[cnt_vert] = startIndex;
cnt_vert++;
} else if (i % 6 == 4) {
if (i > 0 && i % (lapDiv * createSquareFaceCount - 2) == 0) {
//一周したときのループ処理
indices[cnt_vert] = loop1stIndex;
cnt_vert++;
} else {
indices[cnt_vert] = startIndex + 1;
cnt_vert++;
}
} else if (i % 6 == 5) {
if (i > 0 && i % (lapDiv * createSquareFaceCount - 1) == 0) {
//一周したときのループ処理
indices[cnt_vert] = loop2ndIndex;
cnt_vert++;
} else {
indices[cnt_vert] = startIndex + divideX + 1;
cnt_vert++;
}
//開始Indexの更新
startIndex++;
}
}
//底面
if (fov == 360) {
offsetIndex = vertices.Length - 1 - divideX;
int loopIndex = offsetIndex;
for (int i = 0; i < divideX * 3; i++) {
if (i % 3 == 0) {
//底面の先頂点
indices[cnt_vert] = vertices.Length - 1;
cnt_vert++;
} else if (i % 3 == 1) {
indices[cnt_vert] = offsetIndex;
cnt_vert++;
} else if (i % 3 == 2) {
int value = 1 + offsetIndex;
if (value >= vertices.Length - 1) {
value = loopIndex;
}
indices[cnt_vert] = value;
cnt_vert++;
offsetIndex++;
}
}
}
return new MeshData() {
vertices = vertices,
indices = indices,
};
}
}
##実行
さて、これで実行してみましょう。
いかがでしょうか。fovの値を変えると任意の角度の切断球が作られるはずです。
お疲れさまでした！
さて、次の記事ではいよいよ、球面にテクスチャを張り付けていきます。
魚眼レンズ画像をVRに復元する（後編） ～球面の頂点座標のUV座標を調べ、球面の内側にテクスチャを貼り付ける（UVマッピング）～(準備中)