はじめに
**魚眼レンズで撮った映像を、VRヘッドセットで見たい!**というニーズはちょこちょこあると思います。
例えば、

こういった画像だけが手元にあるとき、
このようにOculus RiftやHTC Viveを使って、VRとして見たい!というような需要です。
言い換えると、
魚眼レンズで撮った**平面画像(二次元)を、球体面(三次元)に投影したい!**とも言えるでしょう。
今回は、これをUnityで実現する方法について、説明していきたいと思います。
環境
UnityのバージョンはUnity 2018.2.17を使っています。
(どのバージョンでも特に問題ないと思います。)
また、一部C# 6.0以降の文法を用いています。
大まかなステップ
実現するためのステップとしては、大きく分けて三つあります
ステップ1:メッシュを動的に生成し、丸い球体を作る(プロシージャルモデリング)
このようにメッシュを作り、さらには縦の分割数、横の分割数を変化させ、メッシュの網目の解像度を変更できるようになっています。
プロシージャルモデリング(Procedural Modeling)とは
プロシージャルモデリングとは、ルールを利用して3Dモデルを構築するテクニックのことです。モデリングというと、一般的にはモデリングソフトであるBlenderや3ds Maxなどを利用して、頂点や線分を動かしつつ目標とする形を得るように手で操作をしていくことを指しますが、それとは対象的に、ルールを記述し、自動化された一連の処理の結果、形を得るアプローチのことをプロシージャルモデリングと呼びます。(中略)プロシージャルモデリングを使えば以下のようなことが可能になります。
・パラメトリックな構造を作ることができる
・柔軟に操作できるモデルをコンテンツに組み込むことができる
("Unity Graphics Programming"(IndieVisualLab)より)
ステップ2:球体を任意の中心角N°で切断したものを作る(N°の切断球と呼ぶ)
切断球というのは僕の造語です。この図形を表すいい言葉がなかったので許してください(笑)
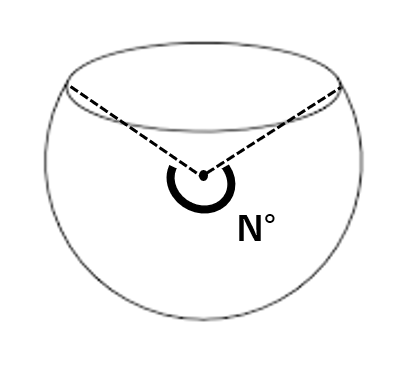
このように球体を刃物で切ったときの形をイメージしてください。
N°というのは、この角度のことを表します。
180°の切断球とはすなわち半球を表し、360°の切断球とはすなわち球体を表します。
魚眼レンズの画角は、360°ではないことも多いので、360°以下の任意の角度に対応できるように、N°の切断球を用意します。
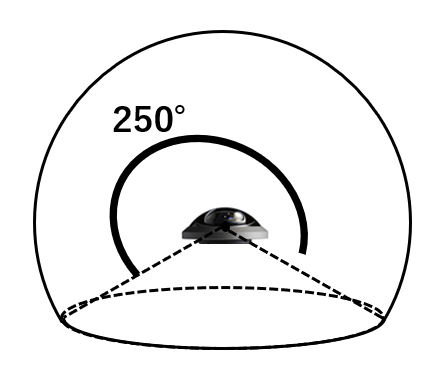
例えば、こちらの魚眼レンズ(Entaniya Fisheye 250)は画角が250°なので、
見えている範囲はこんな感じです。
ちなみに、360°をカバーしている画像は全天球画像や、360°パノラマ写真と言われていますね。
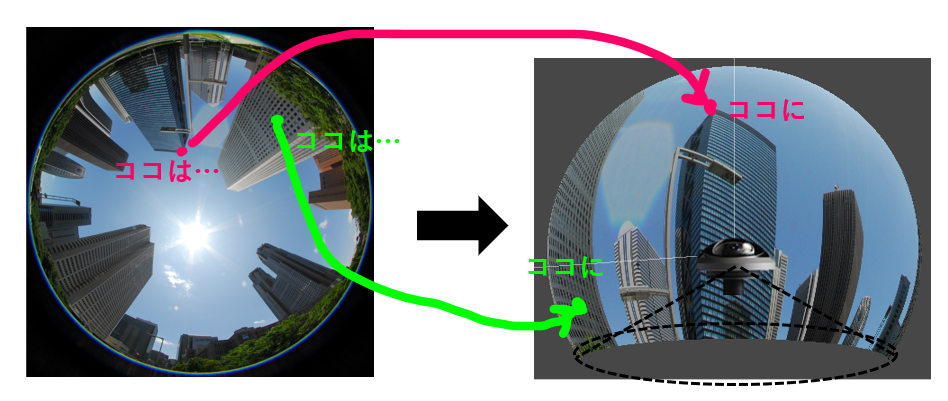
ステップ3:球面の頂点座標のUV座標を調べ、球面の内側にテクスチャを貼り付ける(UVマッピング)
球面上のすべての頂点について、魚眼画像のどの位置と対応しているかを調べます。
これをすべての頂点について行うと、このような球面上に投影されることになります。
つまるところ、平面と球面上の位置の対応関係を調べていく作業となります。
以上、3つのステップが必要になります。
本記事(前編)では、ステップ1をカバーしたいと思います。
ステップ2(中編)、3(後編)については別記事にて近々公開予定です!
ステップ1:メッシュを動的に生成し、丸い球体を作る
完成図はこんな感じです。

動的にメッシュを生成する方法については、こちらの大庭さんの記事を参考にさせていただきました。(ありがとうございます!)
というかステップ1については実はほとんどこちらの記事を踏襲していたりします。
ただ、今回はのちのち魚眼画像という複雑なテクスチャをUVマッピングをしたり、N°の切断球にしたりするためにパラメータ等を工夫しているので、本記事では最初から解説していきたいと思います。
ステップ1-1 変数の確認
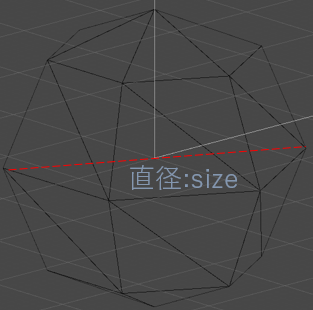
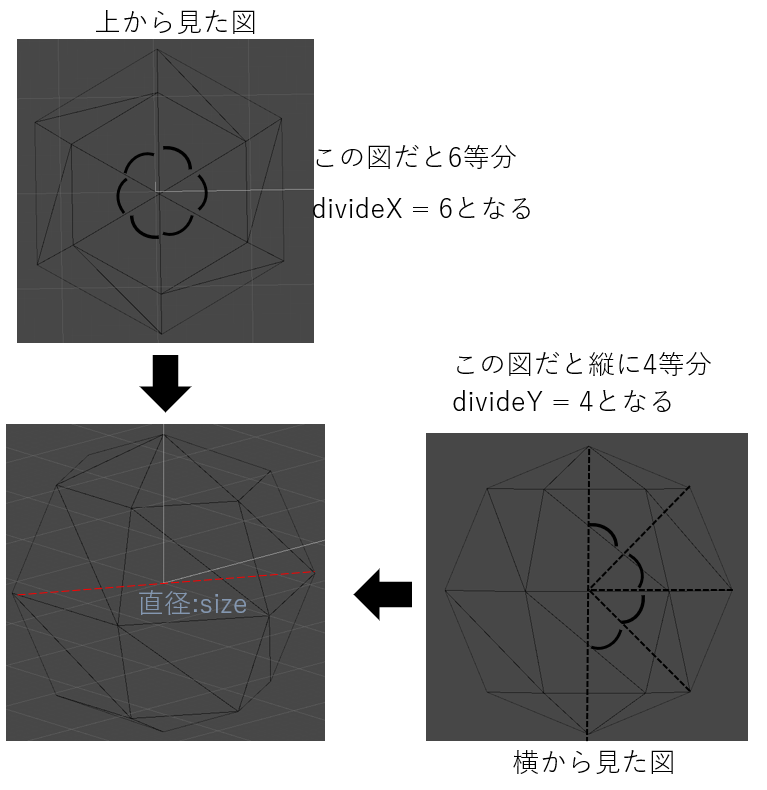
このように、直径sizeの球を、縦と横に分割して考えます。
上から見た時のこの分割数を、divideX
横から見た時のこの分割数を、divideY
このとき、すべての頂点の数vertCountは、
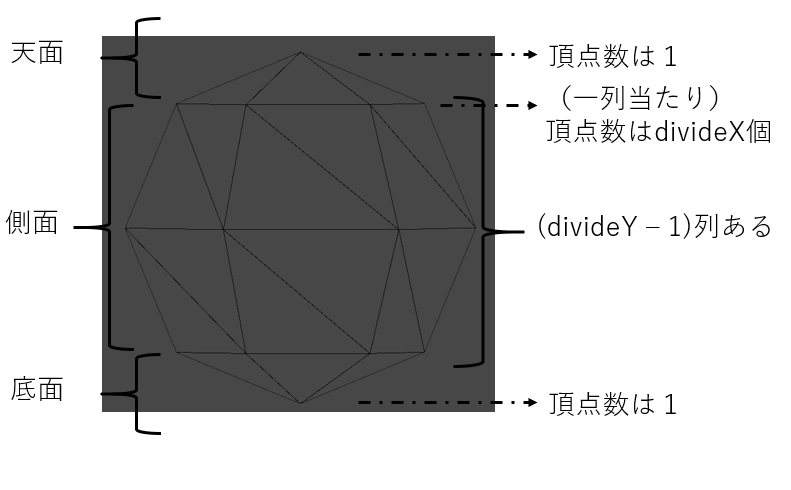
**vertCount = (天面の頂点の数) + (側面の頂点の数) + (底面の頂点の数)**となるので、
それぞれ以下の図から、
計算すると、
vertCount = divideX * (divideY - 1) + 2となります。
よって頂点座標の配列はこのように生成されます。
//頂点の数(天面と底面合わせて)
int vertCount;
vertCount = divideX * (divideY - 1) + 2;
//頂点座標の配列
Vector3[] vertices = new Vector3[vertCount];
一方、頂点インデックスindicesの配列数は全ての面の数を単純に三倍すればよいので、面の数を求めたいです。
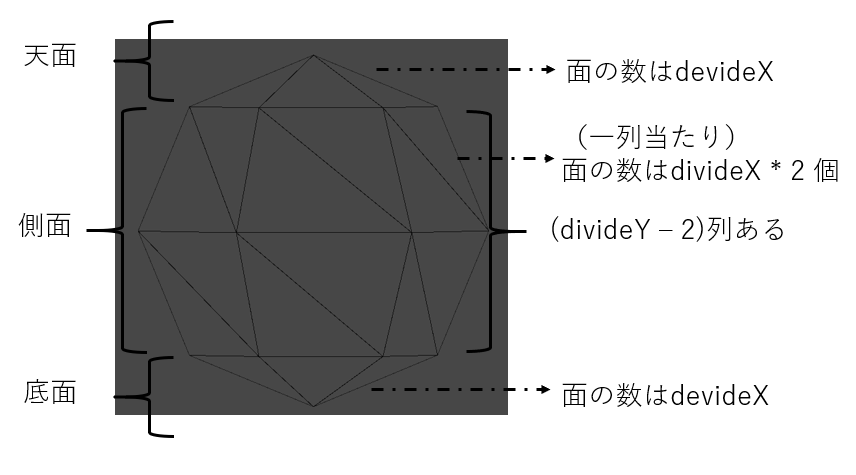
**面の数 = (天面の面の数) + (側面の面の数) + (底面の面の数)**なので、
(天面の面の数) = divideX
(側面の面の数) = divideX * (divideY - 2) * 2
(底面の面の数) = divideX
より、
それら足したものを三倍し、このようになります。
//天面と底面の三角形の数
int topAndBottomTriCount;
topAndBottomTriCount = divideX * 2;
//天面と底面以外の三角形の数
int aspectTriCount;
aspectTriCount = divideX * (divideY - 2) * 2;
//頂点インデックスの配列を生成
int[] indices = new int[(topAndBottomTriCount + aspectTriCount) * 3];
ステップ1-2 準備を整える
さて、ここからはスクリプトを書いていきます。
Unityのプロジェクトを開き、空のGameObjectを作ります。
こちらのGameObjectに、これから作成するスクリプト(DynamicMeshMaker.cs)を貼り付けます。
DynamicMeshMaker.csのひな型がこちら。
using UnityEngine;
[RequireComponent(typeof(MeshFilter))]
[RequireComponent(typeof(MeshRenderer))]
public class DynamicMeshMaker : MonoBehaviour {
private MeshRenderer _renderer;
private MeshRenderer Renderer => _renderer != null ? _renderer : (_renderer = GetComponent<MeshRenderer>());
private MeshFilter _filter;
private MeshFilter Filter => _filter != null ? _filter : (_filter = GetComponent<MeshFilter>());
private Mesh _mesh;
//Materialを保持するようにする
[SerializeField]
private Material _mat;
public Vector2Int divide; //横の分割数、縦の分割数を入れる構造体
public float sphereSize; //球のサイズ
void Update() {
//再生中も変更できるように、毎フレーム更新
Create();
}
[ContextMenu("Create")]
void Create() {
int divideX = divide.x;
int divideY = divide.y;
float size = sphereSize;
MeshData data = CreateSphere(divideX, divideY, sphereSize);
if (_mesh == null) {
_mesh = new Mesh();
}
_mesh.vertices = data.vertices;
_mesh.SetIndices(data.indices, MeshTopology.Triangles, 0);
_mesh.uv = data.uvs;
Filter.mesh = _mesh;
//MeshRendererからMaterialにアクセスし、Materialをセットするようにする
MeshRenderer renderer = GetComponent<MeshRenderer>();
renderer.material = _mat;
_mesh.RecalculateNormals();
}
struct MeshData {
public Vector3[] vertices;
public int[] indices;
public Vector2[] uvs;
}
MeshData CreateSphere(int divideX, int divideY, float size = 1f) {
//
//頂点座標作成
//
//頂点の数(天面と底面合わせて)
int vertCount;
vertCount = divideX * (divideY - 1) + 2;
//頂点座標の配列
Vector3[] vertices = new Vector3[vertCount];
//ここで頂点座標を求めていく
//
//頂点インデックス情報
//
//天面と底面の三角形の数
int topAndBottomTriCount;
topAndBottomTriCount = divideX * 2;
//天面と底面以外の三角形の数
int aspectTriCount;
aspectTriCount = divideX * (divideY - 2) * 2;
//頂点インデックスの配列を生成
int[] indices = new int[(topAndBottomTriCount + aspectTriCount) * 3];
//ここで頂点インデックスを求めていく
return new MeshData() {
vertices = vertices,
indices = indices,
};
}
}
この中の、CreateSphere()の中身を書き加えていきます。
とりあえずステップ1ではUV座標のことは考えないので、頂点座標配列を作る→頂点インデックス配列を作るという流れだけ考えておけばよいことになります。
ステップ1-3 球面上の任意の座標をユークリッド座標で表す
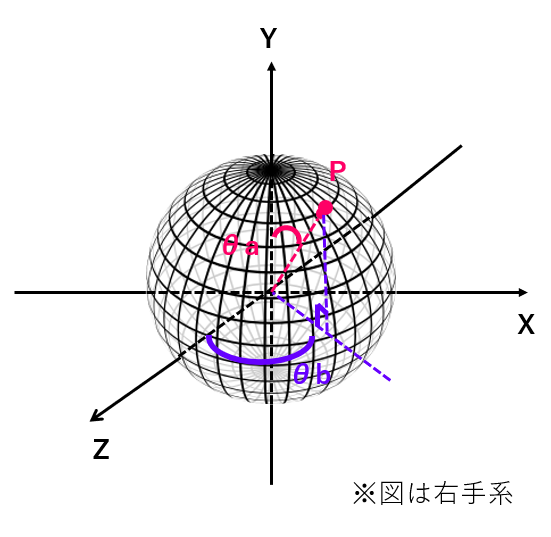
例えば球面上の任意の点Pはユークリッド座標((1, 2, 0)みたいなやつです)でどう表されるでしょうか。
まずはこれを横から見ると、このようになります。
よってPのY座標は半径rとして、r * cosθaです。
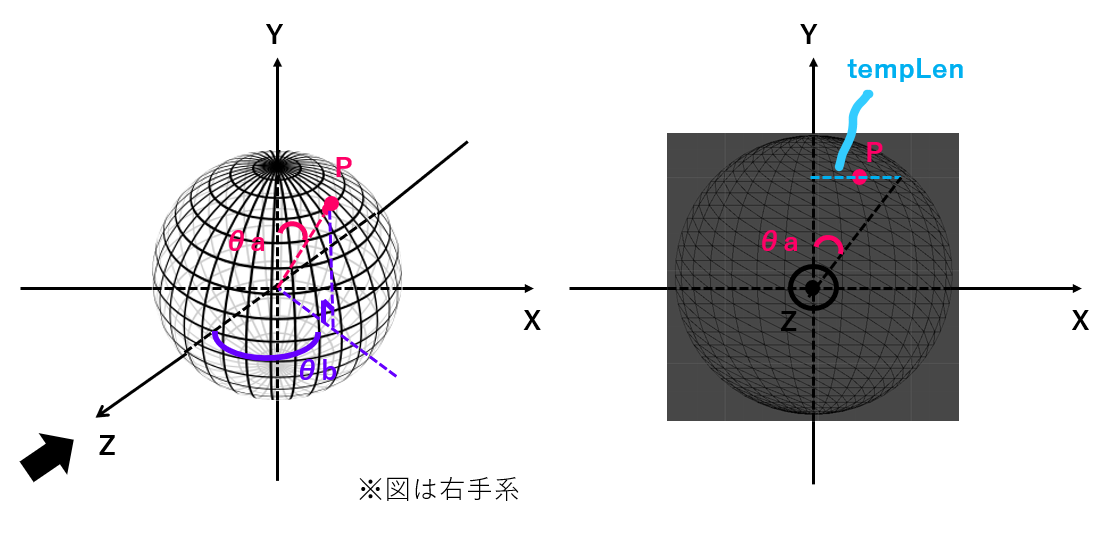
のちのち使うので、上の図の水色の長さをtempLenとおきます。この値は、点PとY軸との距離にあたります。上の図でtempLenの端点がPじゃない理由は、Pの横の一周上の一番遠い点との距離がtempLenにあたるためです。立体をイメージしてもらえるとわかると思います。
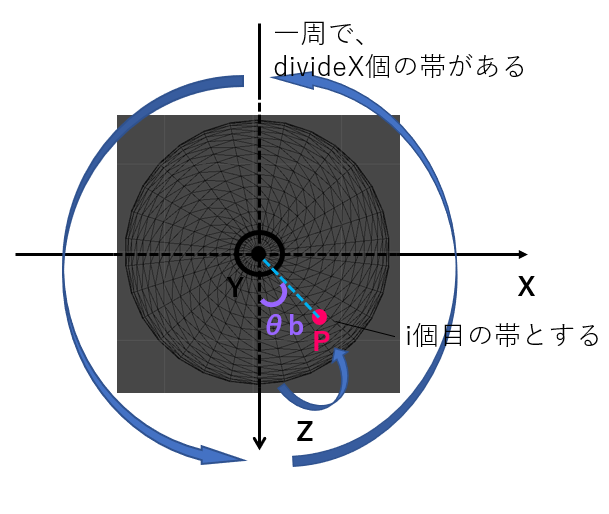
一方で、真上から見るとこのようになります。
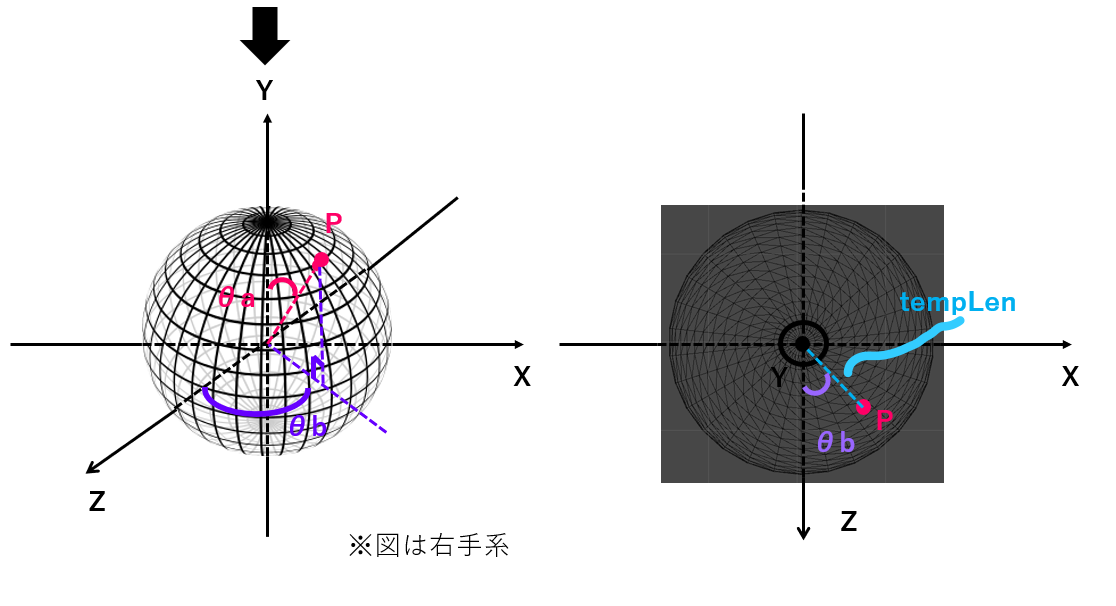
tempLenを用いて、X座標とZ座標はそれぞれこのように表されます。
X座標:tempLen * sinθb
Z座標:tempLen * cosθb
(ただし、tempLen = sinθa)
よって、**P(tempLen * sinθb, r * cosθa, tempLen * cosθb)**と表されることがわかりました。
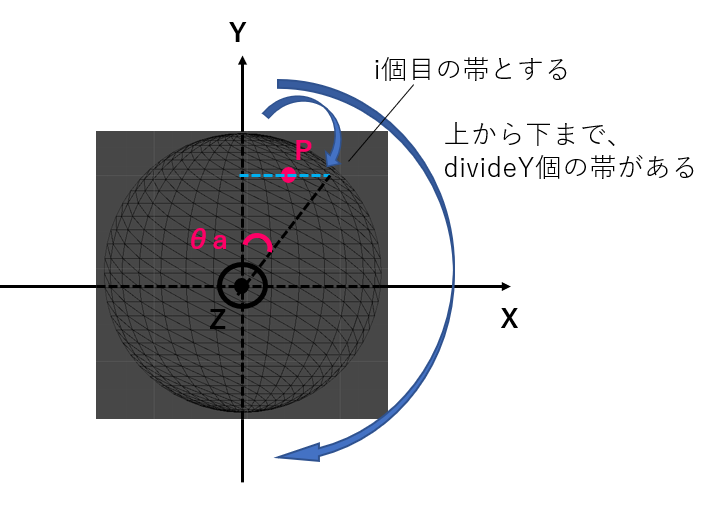
さらに、θaとθbは、それぞれこのように表されます。
θa = (180° / divideY) * iとなります
θb = (360° / divideX) * iとなります
ちょっと最後の図はわかりにくかったかもしれません...
さて、準備は整ったので、いよいよ次の記事から実装に入っていきます。