はじめに

今回は統計学で最も重要な分野である推測統計について説明していきます。

1. 標本調査

標本調査とは以前にも説明しましたが、母集団の一部である標本から母集団の性質を推測する調査のことです。
標本から母集団の性質を推測するのを推測統計といいました。

推測統計をするにあたり重要になってくる考えが、母集団と標本という実世界の話を数学の世界に落とし込んで考えるということです。
標本から母集団を推測するのだと少しざっくりしていてどのような手法で行えばよいのかがわからないと思います。なので母集団を確率分布、標本を確率分布に従う実現値とみなすことで数学的な観点から性質を推測していきます。

つまり今までの推測統計の目的であった「得られた標本から母集団について推測する」は「得られた実現値から、その実現値を発生させた確率分布について推測する」と置き換えることができます。

では数学の世界に落とし込むことでどんなメリットがあるのでしょうか。
一番のメリットは母集団分布のモデル化が行えることだと思います。
母集団分布は未知ですがおそらく真の姿は、多少いびつであったりデコボコした分布になっているかと思います。
しかしこれを数学の世界に落とし込むことで、数式で記述でき数学的に扱える確率分布(正規分布など）で近似して話を進めることができ、母集団の推定が容易になるでしょう。

2. 無作為抽出

データを得る際に、母集団に含まれる要素を１つ１つランダムに選ぶ抽出方法で、別名ランダムサンプリング。
例えば、日本の平均年収を知りたいのに東京だけでデータを抽出したら、間違った平均が推測されるのは言うまでもなくわかると思います。

無作為抽出法にはいくつか手法がありますので、そのうちの一部を紹介します。

単純無作為抽出法
・標本になりうるすべての要素のリストを用意し、乱数を用いてサンプリングする手法。
・全数調査に近いイメージ
・労力とコストが結構かかる
層化多段抽出法
・実際の現場でよく用いられる手法
・母集団をいくつかの層(グループ)に分けておき、各層の中から必要な数の調査対象をランダムに抽出する手法。
多段抽出法(今回の説明は二段抽出法)
・一段目として何かを無作為抽出し、抽出された群の中から対象をさらに無作為に抽出する手法。
・例：全国調査の場合、１段目に都道府県をランダム抽出。２段目に選ばれた都道府県からさらにランダムで抽出。

データの抽出はとても重要で、偏った標本抽出の場合その標本から母集団を正しく推測することはできません。
偏ったデータ抽出になっていないか、データ分析をする前に一度確かめてみるとよいと思います。

3. 標本誤差

母集団平均を$\mu$として、そこから標本を得たとする。標本平均が母平均$\mu$にぴったり一致するのであれば、標本から母集団の平均を言い当てることができることになり、母集団の性質を知ることができたということになりす。
ただ実際に標本平均が母平均$\mu$にぴったり一致することはなく、多少なりの誤差が生じるはずです。これを標本誤差といいます。

※標本誤差は標本抽出における人為的なミスや誤りから生じるものではなく、ランダムに標本を選ぶために生じる避けることのできない誤差です。また平均値に限らず母集団の様々な性質に対して一般的に生じる

推測統計において母集団の性質をぴったり推測することはほぼ不可能だと思っておくことが良いです。なにかしらの誤差が発生していることを許容して推測をするようにしましょう。

続いて標本誤差の分布についても少し説明しておきます。
次章以降の大数の法則や中心極限定理について理解してから、こちらを読むことをお勧めします。

中心極限定理より、標本誤差=$\bar x -\mu$は平均0、標準偏差$\sigma/\sqrt n$の分布に従います。
つまり標本誤差=$\bar x -\mu$の分布は、母集団の標準偏差$\sigma$とサンプルサイズ$n$の2つの値だけで決まることがわかります。
この時の$\sigma/\sqrt n$を標準誤差といいます。
ただここで1点気になるのが、母集団の標準偏差$\sigma$は未知の値なのでこれを用いて計算することはできません。
そこで標本から推定した不偏標準偏差sを$\sigma$の代わりに用いて、$s/\sqrt n$を標準誤差とすればよいでしょう。
不偏標準偏差を数式で表すと次のようになります。

s = \sqrt{\frac{1}{n-1} \Sigma_{i=1}^n \left(x_i - \bar x \right)^2} \

これで標本誤差の分布の説明は以上です。この分布を使うことでどのくらいの大きさの誤差がそれくらいの確率で現れるかを知ることができるようになりました。

4. 大数の法則

標本平均と母集団平均の間に成り立つ法則であり、サンプルサイズ$n$を大きくしていくと標本平均$\bar x$が母集団平均$\mu$に限りなく近づくというというものです。つまり標本誤差=$\bar x - \mu$が限りなく０に近づくということ。

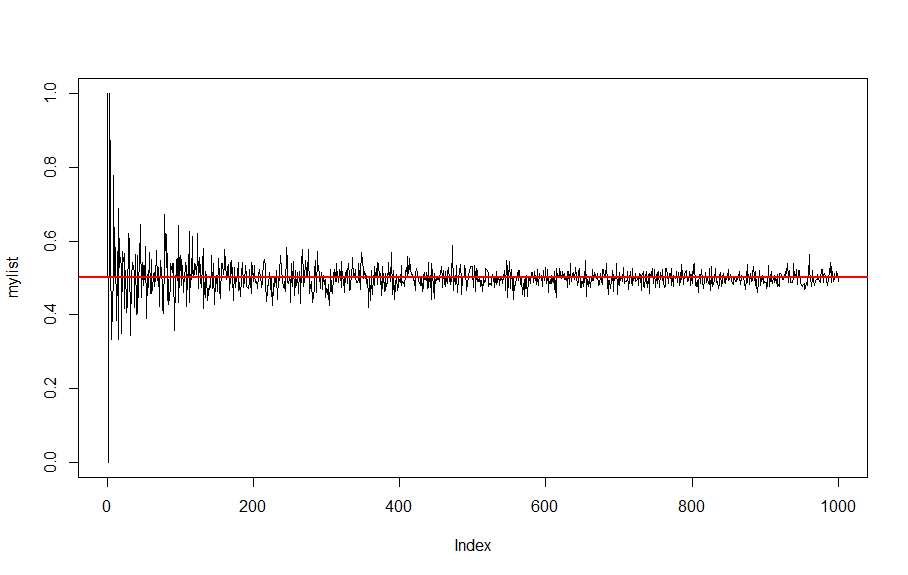
実際にRを用いてコイントスのシミュレーションを実施した。
表：1、裏：0として、サンプルサイズを1~1000回に増やし実際にプロットしました。
赤線が母集団平均=0.5を示しています。グラフを見てわかるように試行回数を増やすほどに標本平均が母集団平均に近づいているのがわかると思います。ただしいくら増やしたところで標本平均が母集団平均とぴったり一致していないこともわかると思います。

5. 中心極限定理

中心極限定理とは母集団がどのような分布であっても、サンプルサイズnが大きいときに標本平均$\bar x$の分布が正規分布で近似できることを意味しています。
「標本平均$\bar x$の分布」という点が少しややこしいですが、サンプルサイズ$n$で標本抽出し標本平均$\bar x$を計算する作業を何度も繰り返し、標本平均$\bar x$を集めてヒストグラムを描くことです。この時サンプルサイズnが大きければ正規分布へと近似ができるといった性質です。

ではこの時近似できる正規分布の２つのパラメータ、平均と標準偏差はどのような値をとるでしょうか。
詳細な証明は省きますが、サンプルサイズnが大きいとき標本平均の分布は、平均：母集団平均$\mu$・標準偏差：$\sigma/\sqrt n$で近似ができます。つまり標準偏差をみるとわかるようにサンプルサイズnが大きくなるほど、ばらつきが小さくなり標本平均と母集団平均の間のズレが小さくなることを意味しています。

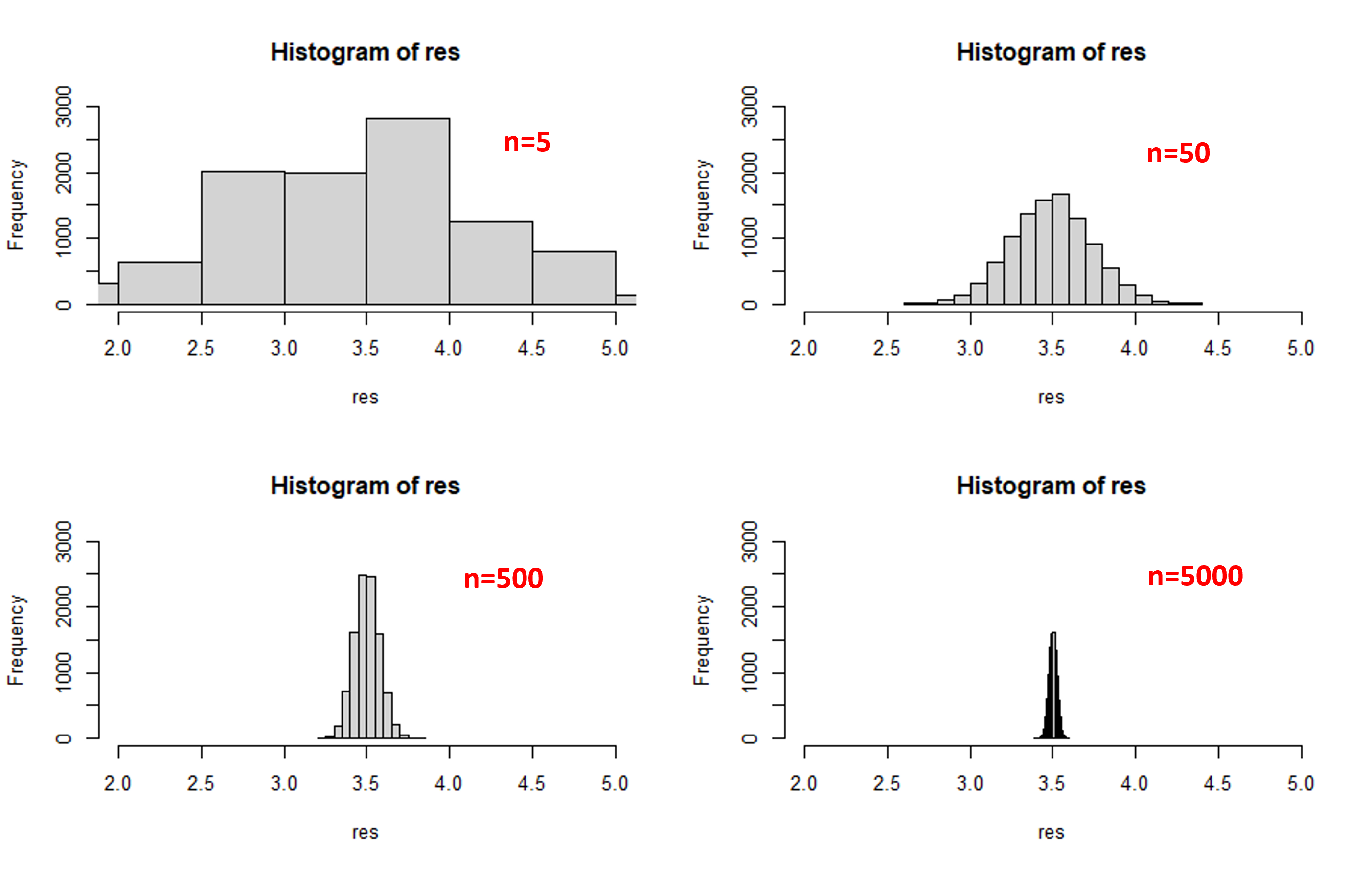
こちらも実際にシミュレーションを実施しました。
今回はサイコロを投げて出た目の平均をとり描画しました。
サンプルサイズ$n=5,50,500,5000$で実施し、各サンプルサイズで$10000$回の標本平均を取得しました。
例えば$n=50$の場合、サイコロを50回投げで出た目の平均をとる作業を10000回実施し、それをヒストグラムで描画しました。

ヒストグラムを見てもらうとわかるように、サンプルサイズを大きくしていくにつれて分布のばらつきが小さく母平均周りに収束していっていることがわかると思います。

6. 推定量

母集団の性質を推定するために使う統計量のこと。サンプルサイズを無限大にしたとき、推定量が母集団の性質に一致する推定量を一致推定量といい、推定量の平均値が母集団の性質に一致する推定量を不偏推定量という。
不偏推定量を数式で表すと以下のようになる。

E[\hat \theta] = \theta

$\theta$を真の値、$\hat \theta$を推定量とする。つまり推定量$\hat \theta$は計算するたびに違う値をとるが、平均的にみると真の値を正しく予測できるような推定量を表します。つまり不偏推定量であることは望ましい推定量であることを示します。

7. 信頼区間

誤差を簡単に定量化するための考えかたを信頼区間といいます。
正規分布の性質を思い出すと、平均値±2×標準偏差の範囲に約95%の値が含まれていましたね。つまりこれは正規分布から1つの値をランダムに取り出すと、約95%の確率でその範囲に含まれるということでした。
この考えをそのまま標本誤差にも適用させたいと思います。

標本誤差の約95%は

0 - 2 × \frac{s}{\sqrt n} \leq \bar x - \mu \leq 0 + 2 × \frac{s}{\sqrt n} \

となる。ここで$\bar x$を移項すると

\bar x - 2 × \frac{s}{\sqrt n} \leq  \mu \leq \bar x + 2 × \frac{s}{\sqrt n} \

となる。

95%信頼区間とは「95%の確率で、この区間が母集団平均$\mu$を含んでいる」ということを示している。
もう少しかみ砕いていうと、母集団から標本を取り出して上記で示した$\mu$に対する95%信頼区間を求める作業を100回実施した時、平均的に95個の信頼区間には母集団平均が含まれるということ。

例えば日本人成人男性の平均身長$\mu$が170cmだとする。このときに、ランダムに選ばれた100人の身長から95%信頼区間を算出する実験を100回行います。
1回目：$150 \leq \mu \leq 175$
2回目：$162 \leq \mu \leq 172$
・
・
・
100回目：$171 \leq \mu \leq 179$
これら100個の信頼区間のうち、5個くらいは母平均である170を含まない範囲のことを示しています。

この信頼区間を用いることで、母集団から標本抽出したサンプルの集計結果がどのくらい誤差を持っているかがわかります。

8. おまけ

推測統計について味噌汁を例におもしろく説明している記事がありましたので、リンクを貼っておきます。
良かったら見てみてください。
https://qiita.com/epppJones/items/7cd8b90da8b59eb60f66

1-4 統計学基礎～推測統計