味噌汁の味見をしたい
皆さんは味噌汁はお好きですか?母が朝早くから作ってくれていたのを思い出します.ところで,味噌汁を作るときに味見をしますよね.実はこの味見というのは**「統計的推定」**に非常によく似ているんです.
**「統計的推定」**とは・・・
母集団からランダムに取り出された標本に基づいて,母集団の性質を表す値(平均や分散)を推定すること
を言います.
先ほどの話でいうところの
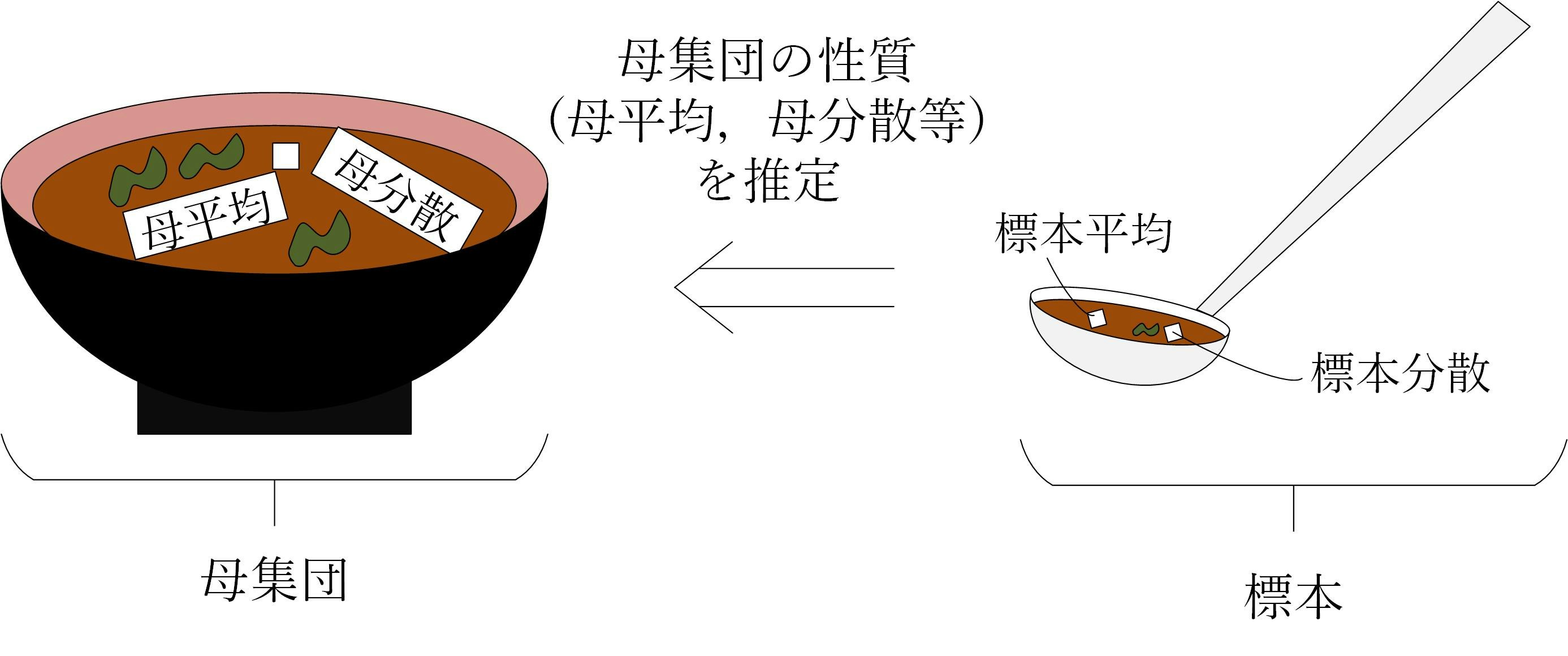
- 母集団 = 味噌汁全体
- 標本 = 味見用に掬い取った少しの味噌汁
- ランダムに取り出す = 味噌汁を(味が均一になるように)よくかき混ぜて取り出す
- 母集団の性質を表す値を推定 = 味噌汁全体の味を見定める
です.つまり,先ほどの定義を「味噌汁の味見」に書き換えると,
味噌汁をよくかき混ぜて取り出された味見用の少しの味噌汁に基づいて,味噌汁全体の味を見定めること
となります(下図,イラストが下手なのはご勘弁ください...).
区間推定とは何ぞや
母集団の未知の母数$\theta$(平均や分散)を,標本の値から適当な"幅"を持たせて推定しようというのが区間推定です.区間推定の場合には,推定の精度を$100(1-\alpha)%$のようにパーセントで表記します.この$100(1-\alpha)%$のことを信頼係数とか信頼区間と呼ぶそうです.
例えば,「母集団の平均身長$\mu$を99%信頼区間で推定したところ$161.2\leq \mu \leq 162.2$となった.」のような場合,より噛み砕いた言い方をすれば
「99パーセントの確率で母平均が161.1~162.2の区間に含まれる」
ということです.

区間推定の方法を教えてほしい
ここでは,母集団が正規分布の場合を考えましょう.求めたい母数$\theta$は母平均だとします.
母平均を求めるにあたって,次の様な2通りの場合が考えられれます.つまり,
- 母分散$\sigma^2$が既知の場合
- 母分散$\sigma^2$が未知の場合
です.
母平均を推定したい!(母分散が既知の場合)
母集団から大きさ$N$の標本$x_1,x_2,\cdots,x_N$を取り出します.この時の母分散$\mu$の$100(1-\alpha)%$信頼区間は
\overline{x}-z\left( \frac{\alpha}{2} \right)\frac{\sigma}{\sqrt{N}}
\leq
\mu
\leq
\overline{x}+z\left( \frac{\alpha}{2} \right)\frac{\sigma}{\sqrt{N}}
となります.ここで,$z\left( \frac{\alpha}{2} \right)$とは,標準正規分布(平均$0$,分散$1^2$)の$(\alpha/2)$パーセント点のことです(下図参照).また,$\overline{x}$は取り出した標本の平均,$N$は取り出した標本数のことです.

ポイントは既知の母分散$\sigma^2$を用いている点ですね.

母平均を推定したい!(母分散が未知の場合)
母分散$\sigma^2$が未知の場合を考えます.この場合は,母分散の代わりに標本分散$s^2$を用いるわけです.
母集団から大きさ$N$の標本$x_1,x_2,\cdots,x_N$を取り出します.この時の母分散$\mu$の$100(1-\alpha)%$信頼区間は
\overline{x}-t_{N-1}\left( \frac{\alpha}{2} \right)\frac{s}{\sqrt{N}}
\leq
\mu
\leq
\overline{x}+t_{N-1}\left( \frac{\alpha}{2} \right)\frac{s}{\sqrt{N}}
となります.$s^2$は先程も述べたように標本の分散で
s^2=\frac{(x_1-\overline{x})^2+(x_2-\overline{x})^2+\cdots+(x_N-\overline{x})^2}{N-1}
また,$t_{N-1}\left( \frac{\alpha}{2} \right)$とは自由度$N-1$のt分布の$(\alpha/2)$パーセント点のことです.$\overline{x}$は取り出した標本の平均,$N$は取り出した標本数のことです.
ポイントは母分散$\sigma^2$が未知なので,仕方なく標本分散$s^2$を用いている点ですね.

なんだよ,やっぱり数学の話がダラダラ続くのかよ
ここまで出てきた標準正規分布やt分布などを聞いてうんざりした方がいるかもしれません.
個人的な話で申し訳ないのですが,私は数学科出身でなく工学系出身です.そのため,統計学はあくまでも道具(ツール)としてとらえています.t分布や標準正規分布については,「ふーん,そんな分布があるんだ」くらいに思っています(本当にそれでいいのかは別として).これらの分布は数表を参照すれば簡単に値が出てきます.
具体例
この記事の締めとして,具体例を見て感動しましょう.
「サラダ油の内容量」
N社のサラダ油800g入りのボトルを9本買ってきました.その内容量を測定したところ,
807g, 811g, 801g, 798g, 798g, 795g, 803g, 805g, 804g
でした.このボトルの内容量の平均は何gでしょう.
母平均$\mu$が99%(の確率で含まれている)信頼区間を求めてみる.もちろん(出荷されたすべてのボトルを購入でもしない限りは分からないので)母分散は未知です.
- STEP1:標本平均$\overline{x}$
\overline{x}=\frac{807+811+801+\cdots+804}{9}=802.4
- STEP2:標本分散$s^2$
s^2=\frac{(807-802.4)^2+(811-802.4)^2+\cdots+(804-802.4)^2}{9-1}=22.25=4.72^2
- STEP3:t分布の$(\alpha/2)$パーセント点
母平均$\mu$が99%(の確率で含まれている)信頼区間を求めたいので,
99=100(1-\alpha)より\frac{\alpha}{2}=0.005
です.データ数$N=9$なので,自由度$N-1=8$のt分布の数表を参照すれば,
t_8(0.005)=3.355
- STEP4:信頼区間
先ほど述べた,母分散が未知の場合の公式
\overline{x}-t_{N-1}\left( \frac{\alpha}{2} \right)\frac{s}{\sqrt{N}}
\leq
\mu
\leq
\overline{x}+t_{N-1}\left( \frac{\alpha}{2} \right)\frac{s}{\sqrt{N}}
を用いると,
\begin{align*}
802.4-3.355\cdot\frac{4.72}{\sqrt{9}}
\leq
&\mu
\leq
802.4+3.355\cdot\frac{4.72}{\sqrt{9}} \\ & \\
797.1\leq&\mu\leq807.7
\end{align*}
が得られました.つまり.N社から出荷された全てのサラダ油800gのボトルは
99%の確率で内容量平均が797.1~807.7gである
というのが分かりました!
参考
石村貞夫著,統計解析のはなし,東京図書,1989年