今更ながら機械学習の学習を始めてみたが、若干とっつきにくかった。
TensorFlowのチュートリアルでまず紹介されるのが文字認識で、初心者おことわりな雰囲気がかもしだされていたことが大きい。
いきなり
「784要素(画素数)の入力データを10要素(数字)の出力データに分配する関数を作ってみよう。膨大(55000個)な手入力データは用意してあるからね。これが機械学習のHello Worldだよ。」
というのはキツかった。
と言いつつも仕方がないので試してみたところ、なんとなくやり方はわかったので、自分なりに租借したチュートリアルを作成してみたので備忘録を兼ねて記す。
Pythonのバージョンは3.5.1を利用した。
作るもの
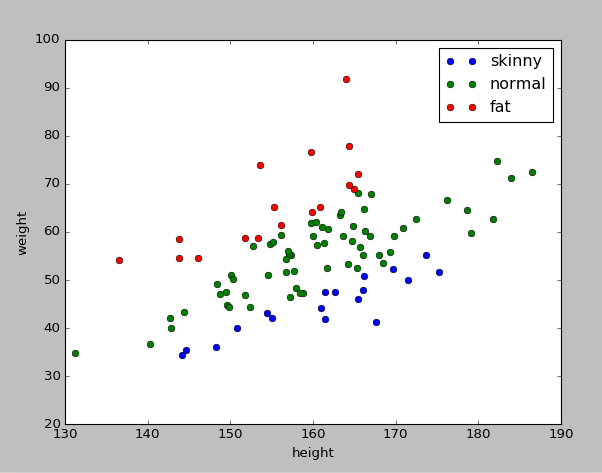
- 身長と体重から体形を「やせ」「普通」「ぽっちゃり」に分類する分配器
想定したシチュエーション
- 多数の人に「身長」と「体重」を聞き出す
- その人の「体形」の印象(個人主観)を「やせ」「普通」「ぽっちゃり」の3分類でメモる
```
172cm 62kg 普通
181cm 55kg やせ
...
```
- メモのデータがある相当数たまったら「身長」と「体重」と「体形」の相関を機械学習させ、「身長」と「体重」さえ判れば直感にたよらなくても体形を判断できるようにする。
TensorFlowによる機械学習の流れ
- 教師データ、及びテストデータを用意する
- 教師データから入力値と出力値のデータ構造を設計する
- 入力値と出力値の相関モデルを仮定する
- モデルに教師データを渡し、学習させる
- モデルの学習状況を確認する
- いくら学習しても正しい結果に近づかない場合は
→ 3.へ戻る
1.教師データ、及びテストデータを用意する
データの相関が分析できる十分なデータ、教師データを用意する。
データ数が多ければ多いほど正確な学習を行うことができる。
Y = f(X)
の$X$と$Y$のセットが教師データ。
$Y$が求め方は判らないけど知りたい情報。
$X$と$Y$はベクトルだけど、難しく考えずに下記のイメージ。
\left(
\begin{array}{ccc}
普通 \\
やせ \\
\vdots
\end{array}
\right)
= f\left(
\begin{array}{ccc}
172 & 62 \\
181 & 55 \\
\vdots & \vdots
\end{array}
\right)
今回の教師データだが、データ形式はCSVにした。
街頭アンケートをする暇がなかったので手で作った。
import numpy as np
import csv
def gen_data(n):
h = 160 + (np.random.randn(n) * 10)
w = (h/100) ** 2 * 22 + (np.random.randn(n) * 10)
bmi = w / (h/100) ** 2
f = np.vectorize(lambda b: 'ぽっちゃり' if b > 25 else '普通' if b > 18.5 else 'やせ')
return np.c_[h, w, f(bmi)]
fp = open('train.csv', 'w')
writer = csv.writer(fp)
writer.writerows(gen_data(100))
fp.close()
172,62,普通
181,55,やせ
...
読み込むのは簡単。
fp = open('train.csv', 'r')
train_data = np.array([r for r in csv.reader(fp)])
train_plot = [train_data[train_data[:,2] == 'やせ'],
train_data[train_data[:,2] == '普通'],
train_data[train_data[:,2] == 'ぽっちゃり']]
plt.plot(train_plot[0][:,0], train_plot[0][:,1], 'o', label = 'skinny')
plt.plot(train_plot[1][:,0], train_plot[1][:,1], 'o', label = 'normal')
plt.plot(train_plot[2][:,0], train_plot[2][:,1], 'o', label = 'fat')
また教師データとは別に、機械学習の学習結果を判定するためのテストデータも用意しておく。
このテストデータは、
$教師データのY = f(教師データのX)$ に限りなく近づくように機械学習された関数
$教師データのY \fallingdotseq g(教師データのX)$
この$g$の性能をチェックするために利用する。
教師データとは異なる$X$を$g$に渡して期待した結果が返ってくるかどうかを見るのである。
チェック内容: $g(テストデータのX)$ が $テストデータのY$ と等しいか
今回は100件の教師データと50件のテストデータを用意した。
2. 教師データから入力値と出力値のデータ構造を設計する
設計と言っても入力値の要素数と出力値の要素数を割りだし、型を決めるだけ。
今回は入力要素が2要素
[ 身長: float, 体重: float]
出力要素が3要素
[ やせである確率:float, 普通である確率:float, ぽっちゃりである確率:float ]
とした。確率は$0$ ~ $1$までの値をとることとする。
CSVから読み込んだデータを下記のように変換。
train_x = np.array([[float(r[0]), float(r[1])] for r in train_data])
train_y = np.array([ [1,0,0] if r[2] =='やせ' else [0,1,0] if r[2] == '普通' else [0,0,1] for r in train_data])
$Y = f(X)$はようするにこうなる。
\left(
\begin{array}{ccc}
0 & 1 & 0 \\
1 & 0 & 0 \\
\vdots & \vdots & \vdots
\end{array}
\right)
= f\left(
\begin{array}{ccc}
172 & 62 \\
181 & 55 \\
\vdots & \vdots
\end{array}
\right)
3. 入力値と出力値の相関モデルを仮定する
ここが肝。
機械学習させる関数$g(X)$を以下のように仮定する。
Y = {\rm softmax}(WX+b)
唐突に式が出てきたが、線形回帰が可能な問題はこれで解ける。
解けない場合については後述。
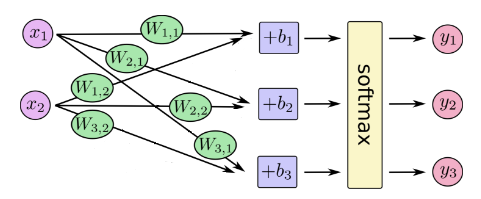
$x_{i}$全てに重み$W_{i,j}$を掛けて、バイアス$b_{j}$を足して${\rm softmax}$すればと$y_{j}$となる関数を用意する。
$W$と$b$を少しづつ変えて教師データの$X$と$Y$の関係に近づけていけば最終的に高性能な分類機になるんじゃないかな、なればいいなという戦略である。
\left(
\begin{array}{ccc}
y_{1,1} & y_{1,2} & y_{1,2}\\
y_{2,1} & y_{2,2} & y_{1,3}\\
\vdots & \vdots & \vdots
\end{array}
\right)
= {\rm softmax}(
\left(
\begin{array}{ccc}
W_{1,1} & W_{1,2} & W_{1,3} \\
W_{2,1} & W_{2,2} & W_{2,3}
\end{array}
\right)
\cdot
\left(
\begin{array}{ccc}
x_{1,1} & x_{1,2} \\
x_{2,1} & x_{2,2} \\
\vdots & \vdots
\end{array}
\right) +
\left(
\begin{array}{ccc}
b_{1} &
b_{2} &
b_{3}
\end{array}
\right))
1行について紐解くと、
$\left(\begin{array}{ccc}やせである確率y_{,1} & 普通である確率y_{,2} & ぽっちゃりである確率y_{,3} \end{array}\right)$
=
{\rm softmax}
\left(
\begin{array}{ccc}
(W_{1.1} x_{,1} + W_{2.1} x_{,2} + b_{1}),\ (W_{1.2} x_{,1} + W_{2.2} x_{,2} + b_{2}),\ (W_{1.3} x_{,1} + W_{2.3} x_{,2} + b_{3}
\end{array}
\right))
$x_{,1}$: 身長、$x_{,2}$: 体重
こういうことである。
${\rm softmax}$が残った。
${\rm softmax}$関数は、今回のように複数の確率値への分類をニューラルネットワークにより行う際に便利な関数である。
数式でいうと$A = \left[\begin{array}{ccc} a_{1} \ldots a_n \end{array}\right]$があったときに${\rm softmax}(A) = \left[\frac{e^{a_{1}}}{\sum_{j=1}^n e^{a_j}} \ldots \frac{e^{a_n}}{\sum_{j=1}^n e^{a_j}} \right]$となる関数であるがとりあえず無視してもらって、
簡単にいうと、配列$A$の合計が$1$になるように、相対的により大きい値は$1$に近づき、小さい値は$0$に近づくように$0$から$1$の範囲で正規化してくれる代物である。
今回は、3つの分類
$[やせである確立,\ 普通である確率,\ ぽっちゃりである確率]$
の組を求めたい。
例えば80%の確率でやせ、20%の確率で普通である身長体重であった場合の答えは
$[0.8,\ 0.2,\ 0.0]$
としたい。
また、教師データの全てのレコードの各合計値も$1$である。
$[1,\ 0,\ 0]\ {\rm or}\ [0,\ 1,\ 0]\ {\rm or}\ [0,\ 0,\ 1]$
そのため、$[1,\ 2,\ 3]$のような結果を出されても収束する気がしない。というかしない。
$[1,\ 2,\ 3]$を${\rm softmax}$すると$[0.09 ,\ 0.245,\ 0.665]$になる。これならいける気がする。
ちなみにこの${\rm softmax}$のように値を正規化する関数のことを機械学習では活性化関数と呼ぶ。
TensorFlowでのモデルの定義は
import tensorflow as tf
# 入力値定義
x = tf.placeholder('float', [None, 2])
# 出力値定義
w = tf.Variable(tf.ones([2, 3]))
b = tf.Variable(tf.zeros([3]))
y = tf.nn.softmax(tf.matmul(x, w) + b)
こうなる。
tensorflowのapiが登場したので軽く説明すると
| api | 説明 |
|---|---|
tf.placeholder |
入力値の定義。 教師データやテストデータはここに入る。実行時に渡してあげる必要がある。 引数は型と次元数。 |
tf.Variable |
学習により変動させる値の定義。 学習を実行する度に誤差が小さくなるように変動する(ようにする) 引数は初期値。 |
tf.ones |
1埋めされた行列を返す |
tf.zeros |
0埋めされた行列を返す |
tf.matmul |
行列の乗算結果を返す |
4.モデルに教師データを渡し、学習させる
先ほどの設定では初期値は適当に設定したため、$X$を渡したとしても適当な結果しか返ってこない。
正しい結果への方向性は予め設定しておく必要がある。
前項で仮定した$g(X)$、$Y= {\rm softmax}(WX+b)$に対し$W$、$b$に初期値、$X$に教師データを代入して計算すると、
\left(
\begin{array}{ccc}
0.333 & 0.333 & 0.333 \\
0.333 & 0.333 & 0.333 \\
\vdots & \vdots & \vdots
\end{array}
\right)
= g\left(
\begin{array}{ccc}
172 & 62 \\
181 & 55 \\
\vdots & \vdots
\end{array}
\right)
このような結果となる。
この結果$Y$と、教師データの真の結果($Y'$と置く)の誤差値を計算し、この誤差値を最小化できれば学習完了である。
確率分布の誤差値は、クロスエントロピーという計算式を使って求められる。
loss = -\sum Y' {\rm log}(Y)
完全一致してれば$0$、違えば違うほど大きい値が取り出せるため、今回はこのクロスエントロピーを誤差値の測定方法として定義した。
次に、モデルでtf.Variable(学習により変動する値)として定義した、$W$と$b$を調整しながら、測定できた誤差値を小さくしていく必要がある。
この誤差値を求める関数(今回でいうと$loss$: $Y$と$Y'$のクロスエントローピー)のことを目的関数と呼ぶ。
目的関数の最適化には様々なアルゴリズムがある。
- 収束は早いが最適解がみつからない可能性が高いアルゴリズム
- 最適解を見つけやすいが収束に時間がかかるアルゴリズム
- ある問題では解をみつけられないアルゴリズム
- パラメータ設定が面倒なアルゴリズム
- など
が、TensorFlowには多くの最適化アルゴリズムの実装が用意されているので、切り替えて試すのは容易である。
今回は勾配降下法(tf.train.GradientDescentOptimizer)とAdam(tf.train.AdamOptimizer)の二つを試したが、どちらとも解を得ることができた。
Adamの方が収束が早かったため最終的にはこちらを選択した。
TensorFlowの最適化アルゴリズムは、目的関数の結果(=誤差値)が小さくなるように、変動値である重み$W$及びバイアス$b$をほんの少しづつ変更してくれる。
一気に変更しても答えはみつからないため、少しづつ変えなければならないが、この変更量はパラメータで調整できる。
大きすぎると答えがみつからず、小さすぎると答えをみつけるまでの時間がかかる。
今回AdamOptimizerへの設定値は0.05が具合がよかった。
TensorFlowでの学習の定義は下記のように行う。
# 教師データの答え入力域(Y')
y_ = tf.placeholder('float', [None, 3])
# 目的関数 -sum(Y'log(Y))
# log(0)はnanを示すため極小量を調整(tf.clip_by_value)
loss = tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(tf.clip_by_value(y, 1e-10, 1.0))))
# 目的関数の結果が最小化されるように変動値を徐々に最適化する
train_step = tf.train.AdamOptimizer(0.05).minimize(loss)
# Variable初期化
init = tf.initialize_all_variables()
sess = tf.Session()
sess.run(init)
train_feed_dict={x: train_x, y_: train_y}
for i in range(100001):
#学習
sess.run(train_step, feed_dict=train_feed_dict)
sess.runを実行すると、第一パラメータの内容が評価される。
その際、そのパラメータを計算するのに必要な、placeholderにマッピングされるデータをfeed_dictパラメータに渡す。
train_stepには教師データの$X$と$Y'$が必要なため上記のように設定する。
学習を10万回実行した。
5.モデルの学習状況を確認する
学習には時間がかかる。
待ったあげく結果がでていなかったら悲しくなるため、設定したモデルが正しく機能しているか、すなわち誤差値が収束に向かっているかを実行中に確認したい。
TensorFlowに可視化のツールとしてTensorBoardが用意されているが今回は触れない。
泥臭くコンソールで可視化した。
test_feed_dict={x: test_x}
for i in range(100001):
sess.run(train_step, feed_dict=train_feed_dict)
if(i % 10000 == 0 or (i % 1000 == 0 and i < 10000) or (i % 100 == 0 and i < 1000) or (i % 10 == 0 and i < 100)):
# 誤差出力
test_y = ['やせ' if max(a) == a[0] else '普通' if max(a) == a[1] else 'ぽっちゃり' for a in sess.run(y, feed_dict=test_feed_dict)]
bools = train_data[:,2] == test_y
print (i, sess.run(loss, feed_dict=train_feed_dict), str(sum(bools) / len(bools) * 100) + '%')
学習回数回数、教師データとの誤差値、及びテストデータの$X$を使用した場合(feed_dictに$Y'$は不要)の正答率を出力している。
出力タイミングは適宜修正。
10 89.8509 64.0%
20 80.4948 64.0%
30 73.6655 64.0%
40 68.4465 65.0%
50 64.4532 69.0%
60 61.0676 73.0%
70 58.317 73.0%
80 56.0346 74.0%
90 54.1317 74.0%
100 52.5213 74.0%
200 44.4377 79.0%
300 41.6028 79.0%
400 40.2241 80.0%
...
このように表示される。
なんとなく学習は成功しているっぽい。
もう少しわかりやすくしたかったため、pyplotでも可視化してみた。
import matplotlib.pyplot as plt
# height: 130~190, weight: 20~100の全組み合わせを作り、学習した関数よりyを取り出す
px, py = np.meshgrid(np.arange(130, 190+1, 1), np.arange(20, 100+1, 1))
graph_x = np.c_[px.ravel() ,py.ravel()]
graph_y = sess.run(y, feed_dict={x: graph_x})
# yをカラーグラデーション(-1 ~ 1)に変換
pz = np.hsplit(np.array([sum(e * [-1, 0, 1]) for e in graph_y]), len(px))
plt.pcolor(px, py, pz)
plt.cool()
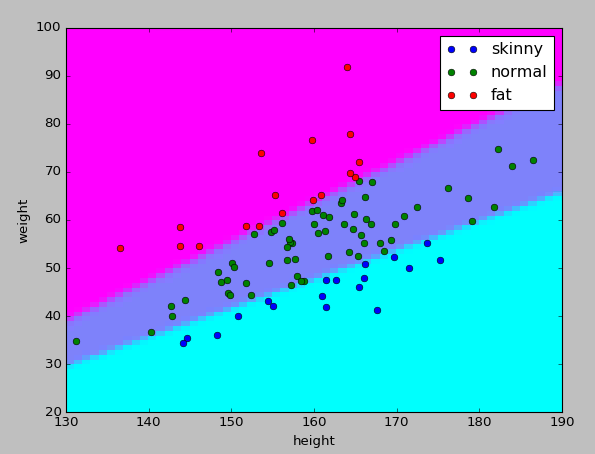
今回の教師データ範囲を身長1cm刻み、体重1kg刻みでとれる全ての組み合わせパターンを$X$とし、モデルに評価させてプロットした。
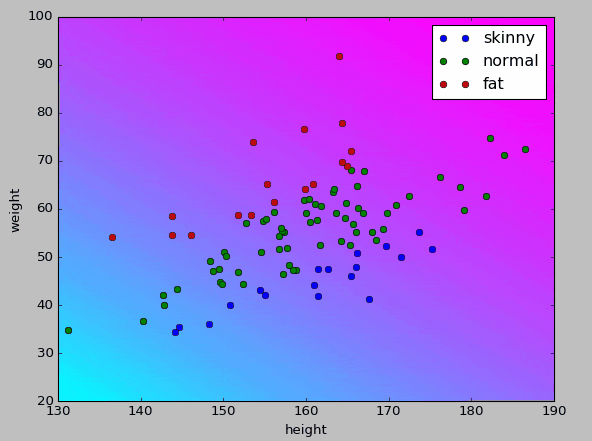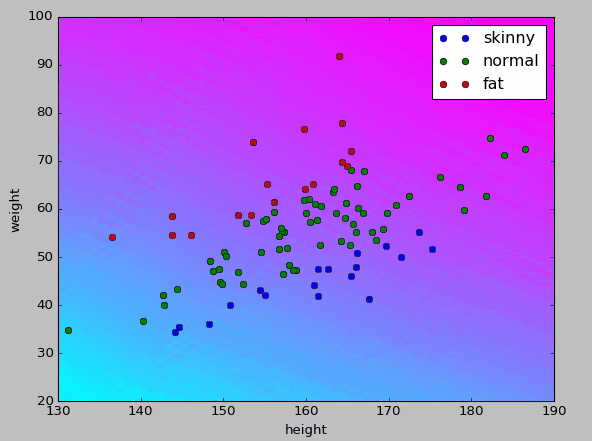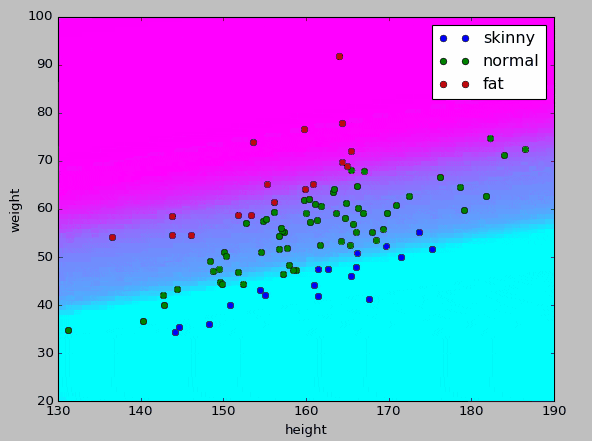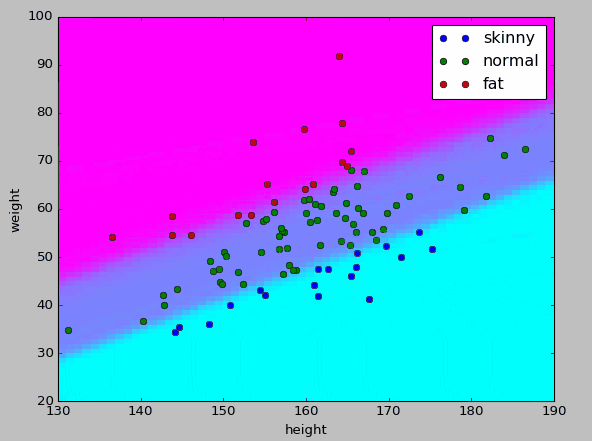
学習の状況としてはこちらの方がつかみやすいのかな、と思う。
6. いくら学習しても正しい結果に近づかない場合は
モデルの設計を見直す。
問題によっては、今回のような単純なモデルでは対応できないため、少しづつ調整を加える必要がでてくる。
詳しくは掴めていないため簡単な例を示すと
学習が遅い、もしくは途中でとまる
- ミニバッチを切る
- 最適化アルゴリズムのパラメータを調整する
- 別のアルゴリズムに変更してみる
期待した結果に近づかない
中間層(hidden層)を追加してみる
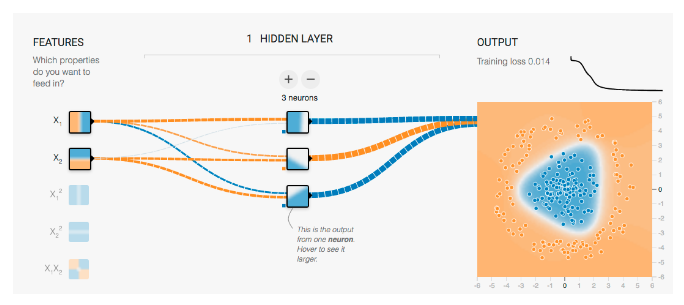
TensorFlow Playgroundの例がわかりやすい
$WX+b$は1次式のため、非線形問題には対応できない。
が、入力層と出力層の間に今回のモデルでは省略した中間層を用意することで、線形モデルの組み合わせにより複雑な非線形モデルを学習させることができるようになる。
時間効率は落ちるが、最終的な誤差値を少なくできる可能性があがる。
中間層追加例
# 中間層
with tf.name_scope('hidden'):
w0 = tf.Variable(tf.ones([2, 4])) #入力層より2つのxを受け取り4つの出力に変換
b0 = tf.Variable(tf.zeros([4])) #それぞれの出力にかかるバイアス
h0 = tf.nn.relu(tf.matmul(x, w0) + b0)
# 出力層
with tf.name_scope('output'):
w = tf.Variable(tf.ones([4, 3])) #中間層より4つの出力を受け取り3つの出力に変換
b = tf.Variable(tf.zeros([3])) #それぞれの出力にかかるバイアス
y = tf.nn.softmax(tf.matmul(h0, w) + b)
入力データを加工してみる
入力データの加工も試す価値があるかもしれない、例えば新たな$x_i$として${x_{1}}^2,\ {\rm sin}(x_{2})$等を追加することで線形回帰可能な問題に変換する。
入力データ加工例
# 入力層
with tf.name_scope('input'):
x = tf.placeholder('float', [None, 2])
#入力値の事前加工
x1, x2 = tf.split(1, 2, x)
x_ = tf.concat(1, [x, x1 ** 2, tf.sin(x2)])
# 出力層
with tf.name_scope('output'):
w = tf.Variable(tf.ones([4, 3])) #[[x1, x2, x1**2, sin(x2)],[skinny, normal, fat]]
b = tf.Variable(tf.zeros([3]))
y = tf.nn.softmax(tf.matmul(h0, w) + b)
入力データを追加する
入力情報が足りない可能性を疑う。
今回の例でいくと、性別、年齢などもデータに追加したらさらに精度が高まるかもしれない。
ただしデータ収集からやりなおしである。
学習結果
今回のモデルでは100件10万回で2分間くらいの計算時間だった。(Core i5 1.8GHz)
...
70000 3.63972 99.0%
80000 3.27686 100.0%
90000 3.02285 100.0%
100000 2.80263 100.0%
8万回目くらいに正答率は100%になった。
グラフもいい感じ
$W$と$b$の値も見てみる
print ('w:',sess.run(w))
print ('b:',sess.run(b))
w: [[ 3.11868572 1.0388186 -0.9223755 ]
[-2.45032024 0.99802458 3.3779633 ]]
b: [-172.08648682 -3.14501309 158.91401672]
分配関数
$(やせである確率, 普通である確率, ぽっちゃりである確率)$
$={\rm softmax}((3.12身長 -2.45体重-172.96), (1.04身長 +体重 -3.15), (-0.92身長 + 3.38体重+158.91))$
の完成である。
念のためipythonで検算
import numpy as np
# softmaxがnumpyになかったので自作定義
def softmax(a):
e = np.exp(np.array(a))
return e / np.sum(e)
def taikei(h, w):
return softmax([(3.12*h - 2.45*w - 172.96), (1.04*h + w - 3.15), (-0.92*h + 3.38*w + 158.91)])
print(np.round(taikei(172,60),2))
↓
[ 0. 1. 0.]
身長172cm、体重60kgだと
100%普通である。
微妙なライン、身長172cm、体重74kgだと
print(np.round(taikei(172,74),2))
↓
[ 0. 0.26 0.74]
74%ぽっちゃりである。
全ソースコード
import numpy as np
import tensorflow as tf
import csv
import matplotlib.pyplot as plt
import math
def read(path):
fp = open(path, 'r')
data = np.array([r for r in csv.reader(fp)])
fp.close()
return data
def convert(data):
return [np.array([[float(r[0]), float(r[1])] for r in data]),
np.array([ [1,0,0] if r[2] =='やせ' else [0,1,0] if r[2] == '普通' else [0,0,1] for r in data])]
train_data = read('train.csv')
test_data = read('test.csv')
# 教師データ表示
plt.xlabel('height')
plt.ylabel('weight')
plt.xlim(130, 190)
plt.ylim(20, 100)
train_plot = [train_data[train_data[:,2] == 'やせ'],
train_data[train_data[:,2] == '普通'],
train_data[train_data[:,2] == 'ぽっちゃり']]
plt.plot(train_plot[0][:,0], train_plot[0][:,1], 'o', label = 'skinny')
plt.plot(train_plot[1][:,0], train_plot[1][:,1], 'o', label = 'normal')
plt.plot(train_plot[2][:,0], train_plot[2][:,1], 'o', label = 'fat')
plt.legend()
train_x, train_y = convert(train_data)
test_x, test_y = convert(test_data)
# 入力層
with tf.name_scope('input'):
x = tf.placeholder('float', [None, 2])
# 出力層
with tf.name_scope('output'):
w = tf.Variable(tf.ones([2, 3]))
b = tf.Variable(tf.zeros([3]))
y = tf.nn.softmax(tf.matmul(x, w) + b)
with tf.name_scope('train'):
#教師データの答え入力域(Y')
y_ = tf.placeholder('float', [None, 3])
#目的関数 -sum(Y'log(Y))
#log(0)はnanを示すため極小量を調整(tf.clip_by_value)
loss = tf.reduce_mean(-tf.reduce_sum(y_ * tf.log(tf.clip_by_value(y, 1e-10,1.0))))
#目的関数の結果が最小化されるように変動値を徐々に最適化する
train_step = tf.train.AdamOptimizer(0.05).minimize(loss)
# Variable初期化
init = tf.initialize_all_variables()
sess = tf.Session()
sess.run(init)
train_feed_dict={x: train_x, y_: train_y}
test_feed_dict={x: test_x}
for i in range(100001):
sess.run(train_step, feed_dict=train_feed_dict)
if(i % 10000 == 0 or (i % 1000 == 0 and i < 10000) or (i % 100 == 0 and i < 1000) or (i % 10 == 0 and i < 100)):
# 誤差出力
test_y = ['やせ' if max(a) == a[0] else '普通' if max(a) == a[1] else 'ぽっちゃり' for a in sess.run(y, feed_dict=test_feed_dict)]
bools = train_data[:,2] == test_y
print (i, sess.run(loss, feed_dict=train_feed_dict), str(sum(bools) / len(bools) * 100) + '%')
# 分類状況表示
# height: 130~190, weight: 20~100の全組み合わせを作り、学習した関数よりyを取り出す
px, py = np.meshgrid(np.arange(130, 190+1, 1), np.arange(20, 100+1, 1))
graph_x = np.c_[px.ravel() ,py.ravel()]
graph_y = sess.run(y, feed_dict={x: graph_x})
# yをカラーグラデーション(-1 ~ 1)に変換
pz = np.hsplit(np.array([sum(e * [-1, 0, 1]) for e in graph_y]), len(px))
plt.pcolor(px, py, pz)
plt.cool()
plt.pause(.01)
print ('w:',sess.run(w))
print ('b:',sess.run(b))
所感
簡単にするつもりがそうでもなかったような気がしないでもない。
pythonは真面目に触ったのは初めてだったが行列演算のやりやすさに感動した。
実用的な機械学習ネタを見つけたいけどなかなかみつからない。