はじめに
この記事では,強化学習において代表的なOff-Policyな学習アルゴリズムとして知られるQ-Learningが,「実際にはどの程度Off-Policyなのか」,ということを実験的に検証してみました.
Q-Learning
Q-Learningはしばしば強化学習の基本的なアルゴリズムとして説明されることが多いアルゴリズムです.
Q-Learningは,以下のような更新式を反復的に繰り返すことによって状態行動価値関数(Q関数)を最適状態行動価値関数へと近づけていきます.
$$Q(s_t,a_t) \gets Q(s_t,a_t) + \alpha (r_t - Q(s_t,a_t) + \gamma \max_a Q(s_{t+1},a))$$
なおここでは,時刻$t$における状態を$s_t$,行動を$a_t$,行動によって遷移したあとの状態を$s_{t+1}$,行動に対して与えられる報酬を$r_t$とします.
Q-Learningの魅力的な点といえばアルゴリズムのシンプルさや実装のしやすさが挙げられることが多いですが,個人的には「無限に反復を繰り返せばQ関数は必ず最適なQ関数へと収束する」という理論的な保証があることも非常に素晴らしい点だと思います.
Off-Policy
Q-Learningのような強化学習アルゴリズムでは,環境内で行動を何回か取ってみて学習のためのデータ${(s_t,a_t,s_{t+1},r_t)}$を集め,そのデータを用いてQ関数の更新のような学習を行う,という流れを繰り返すことで学習を行っていきます.
Q-Learningでは,$\epsilon$-greedyやボルツマン分布によって行動を選択することで,Q関数の学習のためのデータを集める,ということが一般的になっています.ただし,絶対に$\epsilon$-greedyのような行動選択方法でデータを集めなければならない,というわけではなく,理論的には「すべての状態ですべての行動を十分選択できるような行動選択方法」によって行動を取ったとしてもQ関数の収束が保証されています.このような強化学習アルゴリズムのことをOff-Policyであると表現します.1
これはつまり,無限に学習時間があるなら完全にランダムに行動を選択したとしてもQ関数が収束する,ということを意味しています.もちろん,実用上はランダムに行動を選択した場合,そんなに重要でない状態についてのデータばかり集めることがありそうなので,あまり学習の効率はよくなさそうです.また,一度の失敗も許されないようなゲームの場合,そもそもランダムに行動を取っていては現実的な時間ではステージの奥深くに進むことができず,到達できないような状態が出てきてしまうことが予想されます.これではいつまで経ってもゴールにたどり着くように学習が進まないため,この観点からもランダムな行動選択を用いた場合の学習効率が悪そうなことがわかります.
理想的には最適な政策2に非常に近い政策に従って行動を選択できれば良さそうですが,実際にはどの程度最適な政策に近ければ学習効率が良くなり,逆にどの程度最適な政策から離れてしまうと学習効率が悪化してしまうのでしょうか??
今回は簡単な迷路を探索するタスクにQ-Learningを適用することによって,「学習のためのデータを集める政策を変化させたときに学習効率がどのように変化するのか」を実験的に確認したいと思います.
実験
迷路探索タスク
迷路探索タスクは,エージェントが以下のような迷路を探索してゴール地点に到達することを目指すタスクです.

エージェントは,スタート地点「S」からゴール地点「G」へと移動することを目指します.エージェントはエピソードの各ステップごとに,今いるマスから上下左右の隣接したマスに移動することができます.ただし,エージェントは黒色の壁に移動しようとした場合には移動できず,その場にとどまるものとします.
エージェントはゴール地点に到達した場合に$+1$の報酬を,壁に移動しようとした場合に$-1$の報酬を受け取ります.エージェントがゴール地点に到達する,または計1000回移動した場合,そのエピソードは終了し新しいエピソードが開始します.
設定
$\epsilon$-greedyのパラメータは$\epsilon=0.05$に設定し,Q値の初期値はそれぞれ$[0,1]$の範囲でランダムに決定するようにしました.学習は各実験ごとに$100,000$step行いました.
迷路1
まずはじめの実験では,$\epsilon$-greedyによって行動を選択する政策とランダムに行動を選択する政策の比較を行います.
迷路の構造はこちらの記事を参考にして,上述の画像のように設定しました.
学習データを集める政策として**$\epsilon$-greedyによって行動を選択する政策**を用いた場合の結果は以下のようになりました.この図は,学習中のエージェントが迷路のゴールにたどり着くまでのステップ数の推移を表しています.goal stepが1,000stepとなっている場合はゴールに到達できずにエピソードが終了してしまったことを表しています.
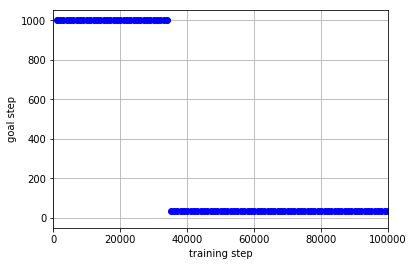
学習データを集める政策としてランダムに行動を選択する政策を用いた場合の結果は以下のようになりました.

この結果から,「ランダムに行動を選択する政策」よりも「$\epsilon$-greedyによって行動を選択する政策」を用いたほうが効率よく学習を行えていることがわかります.
迷路2
次の実験では,「迷路1」を学習させることによって得たQ関数に従って$\epsilon$-greedyに行動を行う政策と**$\epsilon$-greedyによって行動を選択する政策**の比較を行います.
迷路2の構造はつぎのように設定しました.迷路1のスタート地点とゴール地点を入れ替えただけのものですが,ほぼ真逆の方向へと進まないといけなくなるため,「迷路1」と「迷路2」は本質的に全く異なるタスクとなっています.

学習データを集める政策として**「迷路1」を学習させることによって得たQ関数に従って$\epsilon$-greedyに行動を行う政策**を用いた場合の結果は以下のようになりました.
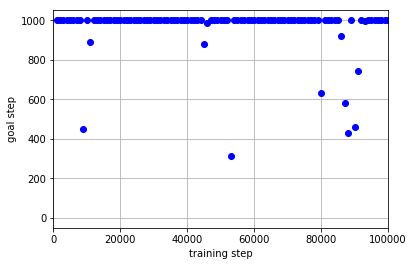
学習データを集める政策として**$\epsilon$-greedyによって行動を選択する政策**を用いた場合の結果は以下のようになりました.
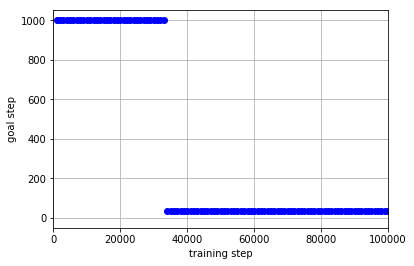
この結果から,学習のためのデータを集める政策として「迷路1」によって学習済みの政策を用いた場合,学習が進まなくなってしまっていることがわかります.これは「迷路1」と「迷路2」がスタート地点とゴール地点が入れ替わっているために,まったく違うタスクとなっていることが要因と考えられます.全然異なるタスクである「迷路1」の学習済みの政策では「迷路2」のゴール地点に到達することが困難であるため,「迷路2」のゴールへのたどり着き方がうまく学習できなかったようです.
迷路3
最後の実験では,「迷路1」と構造を近いものにした上で,再度**「迷路1」を学習させることによって得たQ関数に従って$\epsilon$-greedyに行動を行う政策と$\epsilon$-greedyによって行動を選択する政策**の比較を行います.
迷路3の構造はつぎのように設定しました.ゴール地点の位置が「迷路1」のものから微妙に異なっていますが,「迷路1」と「迷路3」はほとんど同じタスクであることがなんとなくわかります.

学習データを集める政策として**「迷路1」を学習させることによって得たQ関数に従って$\epsilon$-greedyに行動を行う政策**を用いた場合の結果は以下のようになりました.
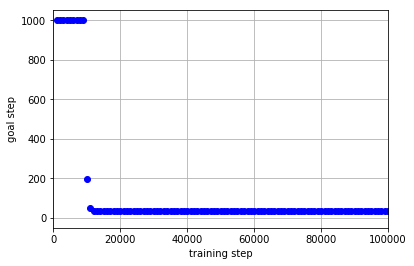
学習データを集める政策として**$\epsilon$-greedyによって行動を選択する政策**を用いた場合の結果は以下のようになりました.
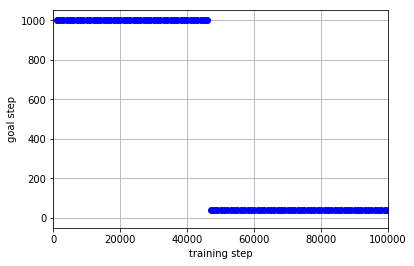
「迷路2」の実験と違い,学習のためのデータを集める政策として「迷路1」によって学習済みの政策を用いた場合,学習効率が良くなっていることがわかります.これは「迷路1」と「迷路3」が非常に似たタスクであるため,「迷路1の学習済みの政策」も「迷路3の最適な政策」と似通ったものになっていることが要因であると考えられます.
おわりに
迷路探索タスクを通した実験によって,Q-Learningの学習のためのデータを集める政策が最適な政策に近い場合,$\epsilon$-greedyと比べて学習の効率が良くなることがわかりました.一方で,最適な政策とあまりに離れている場合,かえって学習効率が悪化する可能性があることもわかりました.
ゲームなどを学習させる場合,人間によるプレイログを用いてQ関数を事前学習させる,ということがしばしば行われます.今回の結果から,人間のプレイログが質が良いものになっていることが重要であると考えられます.あまりにも下手なプレイヤによるプレイログの場合学習効率をかえって悪化させてしまうため,学習のためのデータとして用いないほうが良い,というケースもありそうです.