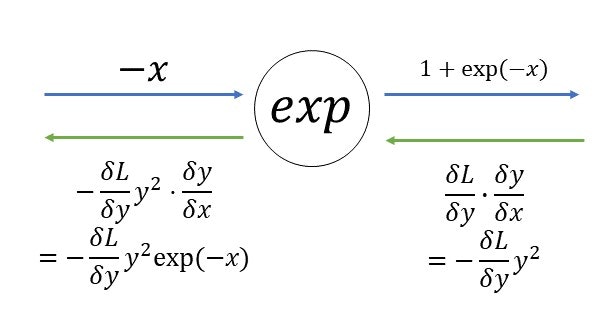Pythonの勉強はしていたけど、DeepLearningに関しては一切勉強をしていなかった私ですが、今回DeepLearningの勉強をすることになったので、その中でつまずいたところや、すぐに理解できなかったこと、メモしておきたいところを残していきたいと思います。
私と同じようなところでつまずいた方や、パッと確認したい、みたいな方がいたら、なんとなく使っていただけたら嬉しいです。
今回、私が使った本は ***「ゼロから作るDeep Learning」***です。
再度確認しておきますが、本書で勉強を始める前の私の理解度は、
- Pythonは多少理解している
- 本書だと、1章の1.4までを読む前から理解している状態
- ２章も学校の授業であらかじめ理解している
- 高校の数学レベルの内容も理解している
- 本書だと、４章の4.2や4.3の微分の部分
- Deep Learningに関しては全くの初心者である
- 行列・配列の計算や考え方、偏微分は存在だけを知っているが、中身はあまり知らない
といった具合です。
本記事の流れ:
1.「対応する行列の次元数を一致させる」の認識
2.勾配の考え方
3.前方差分より中心差分の方がいい理由
4.関数一覧
5.逆伝播のレイヤまとめ
6.まとめ
また、この記事は、「ゼロから作るDeep Learning」を読んでいることを前提として、必要最低限の情報のみで構成しています。
##1.対応する行列の次元数を一致させる
３章 3.3 多次元配列の計算で１番初めに出てくるこの言葉ですが、私にはあまりピンときませんでした。
感覚的には何となく理解できていたし、実際に計算するときもそんなに苦労しなかったのですが、ちゃんと理解できていたかと聞かれれば、"感覚"でずっと考えていた、という感じでした。
本の説明では、
行列Aの１次元目の要素数(列数)と行列Bの０次元目(行数)を同じ値にする必要があります
と書いてあります。
ですが、たまに行列Aの０次元目の要素数(行数)と行列Aの1次元目(列数)を同じ値にして計算している場面がありました。
別に、感覚的に理解できなくはないので
(ああ、そういうもなんだな)
と思って読み進めていましたが、自分なりの結論が出たので、メモしておきます。
(行列Xの１次元目の要素数, 行列Yの0次元目の要素数)
が
$(a, a)$
という形になるようにする
（補足）
X, Y:は行列A, Bどちらでもよい
(例えば、行列Bの1次元目の要素数、行列Aの0次元目の要素数という形でもよい)
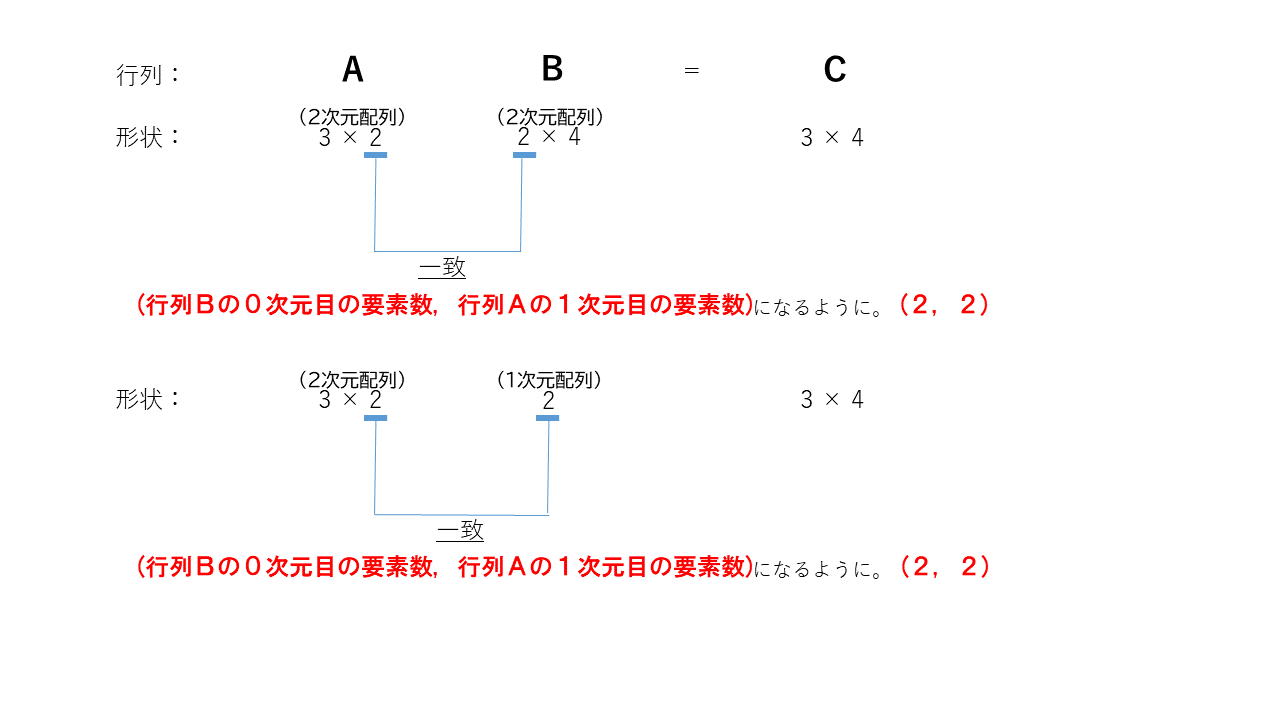
です。自分的には、この考え方が一番しっくりきました。
理解した後に、もう一度、
行列Aの１次元目の要素数(列数)と行列Bの０次元目(行数)を同じ値にする必要があります
を読んだら、すごくしっくりきました。
##2.勾配の考え方
偏微分の勉強をしていなかったので、私にはこの勾配の考え方をつかむのにすごく時間がかかりました。
本の説明では
勾配が示す方向は、各場所において「関数の値を最も減らす方向」なのです。
と書いてあります。
・関数の値を最も減らす方向ってなに？？？
という疑問を持ち続けて勉強を進めていました。
そんな私が勾配に対して違和感なく考えられるようになったのは
-
勾配ってなんだ
-
Deep Learningにおいて微分が何を示しているのか
を理解できるようになったからだと思います。
###◎勾配ってなんだ
そもそも微分とは、ある１点における接線の傾きを表すものです。
微分をして出てきた値が、正の向きに大きくなる時の方向を示しています。
例えば、
$$ y = x^2 $$
という式の微分は
$$ y' = 2x $$
になります。
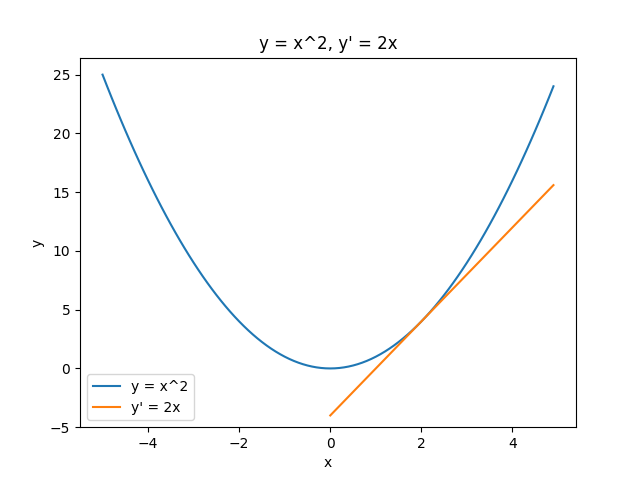
x = 2 の時、 y = 4 になり、この場合は右斜め上方向に大きくなっていくことを示すことができます。
この場合、x の値が変更されることで y の値が決まるため、変数は x のみの1つ、 y は定数となります。
この変数の部分が複数ある場合の微分を、偏微分と言います。
この偏微分を使って、ベクトル表示でまとめたものが、勾配となります。
こう言われても、初めは全く理解ができません。
私は理解ができませんでした。
最後にまたここに戻ってきたときに、私は理解することができたので、1番初めに書いておきます。
###◎Deep Learningにおいて微分が何を示しているのか
ディープラーニングとは、層を深くしたディープなニューラルネットワーク
と8章の初めに書いてあります。
ニューラルネットワークの学習の流れは
1. データをランダムに取り出して推論処理を行う(forword propagation)
2. 誤差逆伝播を使って勾配を求める(backword)
3. 勾配を基に重みパラメータを操作(更新)する
という感じです。
そもそも、ニューラルネットワークの学習の目的は、**「損失関数の値をできるだけ小さくするパラメータを見つけること」であり、これはすなわち「最適なパラメータを見つける」**ということになります。
つまり、
最適なパラメータとは、その関数の最小値である
と言えます。
そして、この
関数の最小値への方向を示してくれるのが、勾配
なのです。
これに気づいたときに、パズルのピースがはまった感覚になりました。
勾配を求めるためには、偏微分が必要で、偏微分には、微分が必要になる、ということになるのです。
##3.前方差分より中心差分の方がいい理由
4章 4.3数値微分で、
- 小さすぎる値を用いるため、丸め誤差が起きてしまう
- 丸め誤差:少数の小さな範囲において数値が省略されることで、最終的な計算結果に誤差が生じてしまう
という記述があり、
小さすぎる値を用いることはコンピュータで計算する上で問題になる
ことがわかります。
これを改善するために「前方差分より、中心差分を用いた方がいい」という風に書いてあります。
前方差分とは、
$$\frac{df(x)}{dx} = \lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$$
で表されるように、(x + h)と x の差分から求めるものです。
それに対し、
中心差分とは、
$$\frac{df(x)}{dx} = \lim_{h \to 0}\frac{f(x+h)-f(x-h)}{2h}$$
で表されるように、(x + h)と(x - h)の差分から求めるものです。
私の目には、前方差分((x + h) と x の差分)の方が、中心差分((x + h)と(x - h)の差分)の方が、誤差が少なく済むように感じました。
これに関しては、きちんと証明して、まとめてくださっている記事があるので、そちらを紹介させていただきます。
紹介したい記事
証明がめちゃめちゃわかりやすかったです。
##4.関数一覧
ここからは本当にメモです。
私がわかりやすいように、区別がつきやすいように書いていきます。
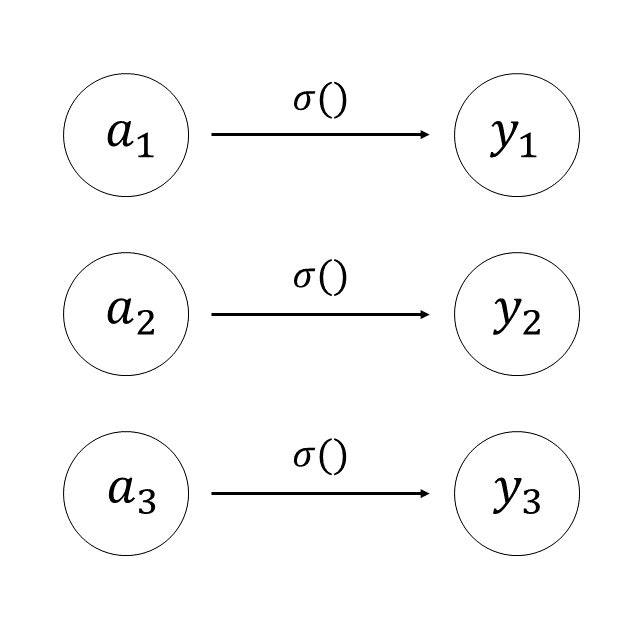
4.1 活性化関数
隠れ層
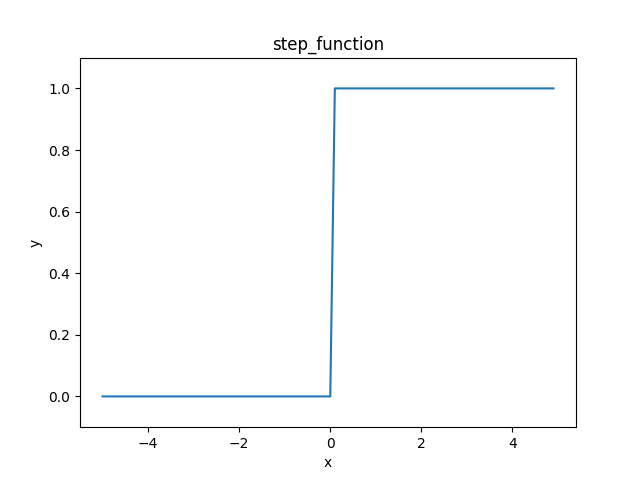
1.ステップ関数
見た目がジャギジャギしてる。
階段状のグラフになる。
入力が0を超えたら1を出力し、それ以外は0を出力する
$$y=h(b+w_1x_1+w_2x_2)$$
h(x) = \left\{
\begin{array}{ll}
1 & (x \leqq 0) \\
0 & (x > 0)
\end{array}
\right.
2.sigmoid関数
見た目が滑らかなやつ。
ステップ関数の欠点を補っている。
2クラスの分類問題の出力層に使われる。
$$h(x)=\frac{1}{1+\exp(-x)}$$
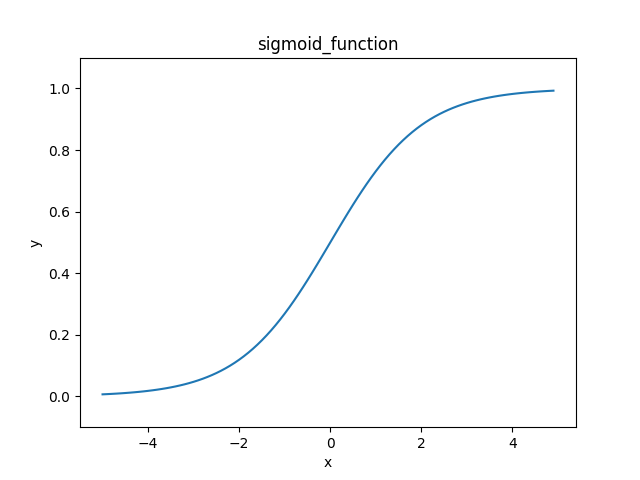
似たもので、tanh関数がある。
これは、sigmoid関数と同じで、S字のカーブを描く関数。
- sigmoid関数
- $(x, y) = (0, 0.5)$において対称
- tanh関数（双曲線関数）
- $(x, y) = (0, 0)$、原点において対称
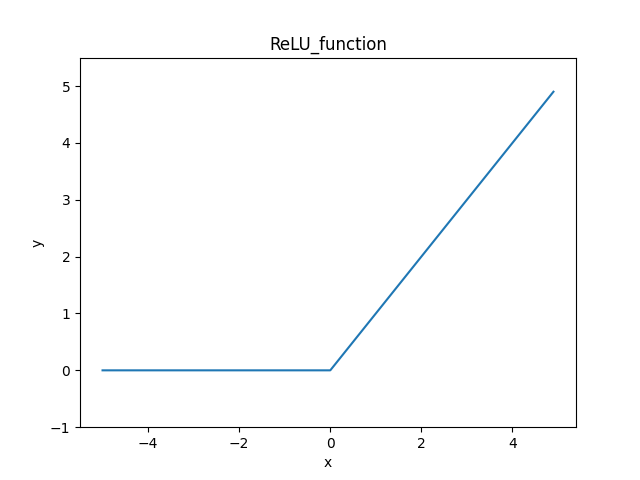
3.ReLU関数
よく使われているやつ。
今でも使われている優秀な関数。
入力が0を超えていれば、入力をそのまま出力し、0 以下ならば0を出力する関数
h(x) = \left\{
\begin{array}{ll}
1 & (x > 0) \\
0 & (x \leqq 0)
\end{array}
\right.
出力層
4.恒等関数
入力をそのまま出力する。
回帰問題の出力層に使われる。
5.ソフトマックス関数
多クラス分類の出力層に使われる。
最終的に、確率っぽい形で出力する。
(それが実際の確立と互換性があるかは、2020.12現在、まだわからない。けど、確率っぽい形で出力してくれるから、とても使いやすい。)
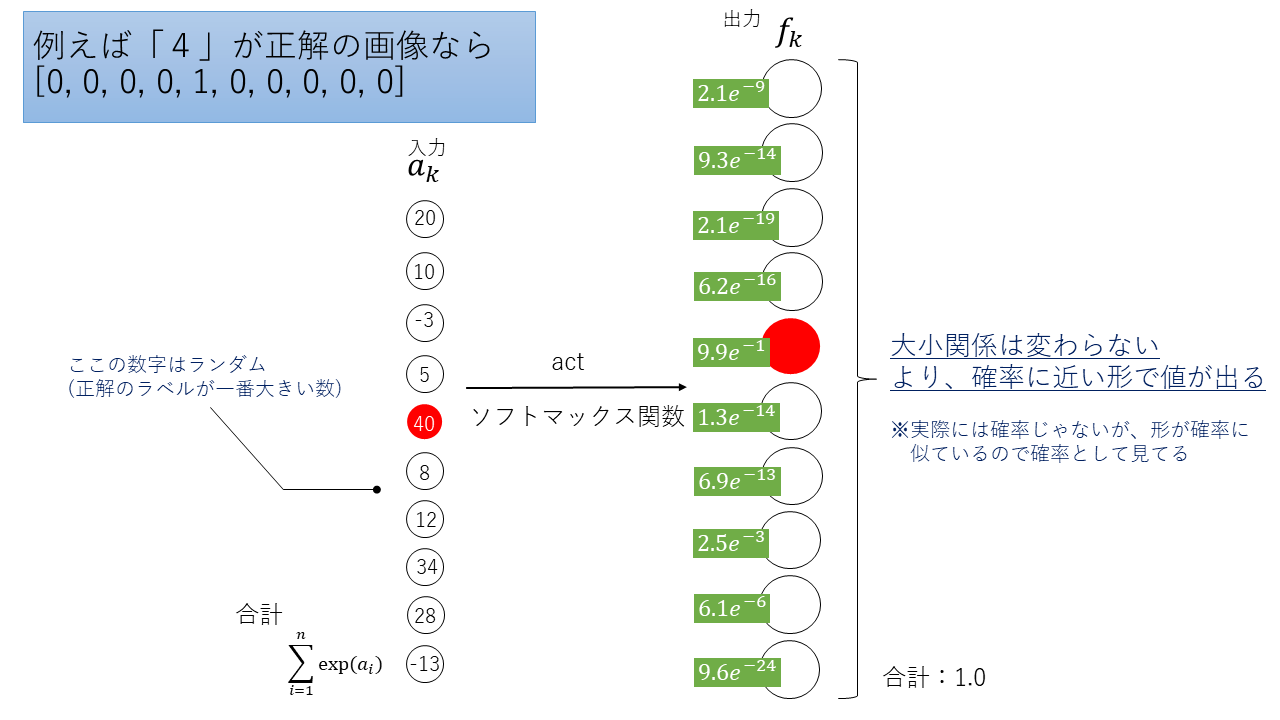
y_k=\frac{\exp(a_k)}{\sum_{i=1}^{n}\exp(a_i)}
本来は、$y_k=\frac{a_k}{\sum_{i=1}^{n}a_i}$としたいけど、これだと値の差が狭くなりすぎて、確率っぽい形にならない。
正解のラベルのみ、値を大きくして、そうじゃないラベルの値はとても小さくしたい。
そうすることで、正解と正解じゃないラベルがはっきりと区別されるため、より確率っぽい形になるので、exponential(exp)を付ける。
4.2 損失関数
ニューラルネットワークが出した結果と正解ラベルとの差
ニューラルネットワークの信頼性を上げるためには、ここを最も小さくしていく。
##5.逆伝播のレイヤまとめ
5章の誤差逆伝搬で何ぺージにもわたって書かれていた逆伝搬の各ノードまとめです。
ページをめくるのがめんどくさいので、ここでまとめます。
関数同様、こちらも私がわかるためのメモです。
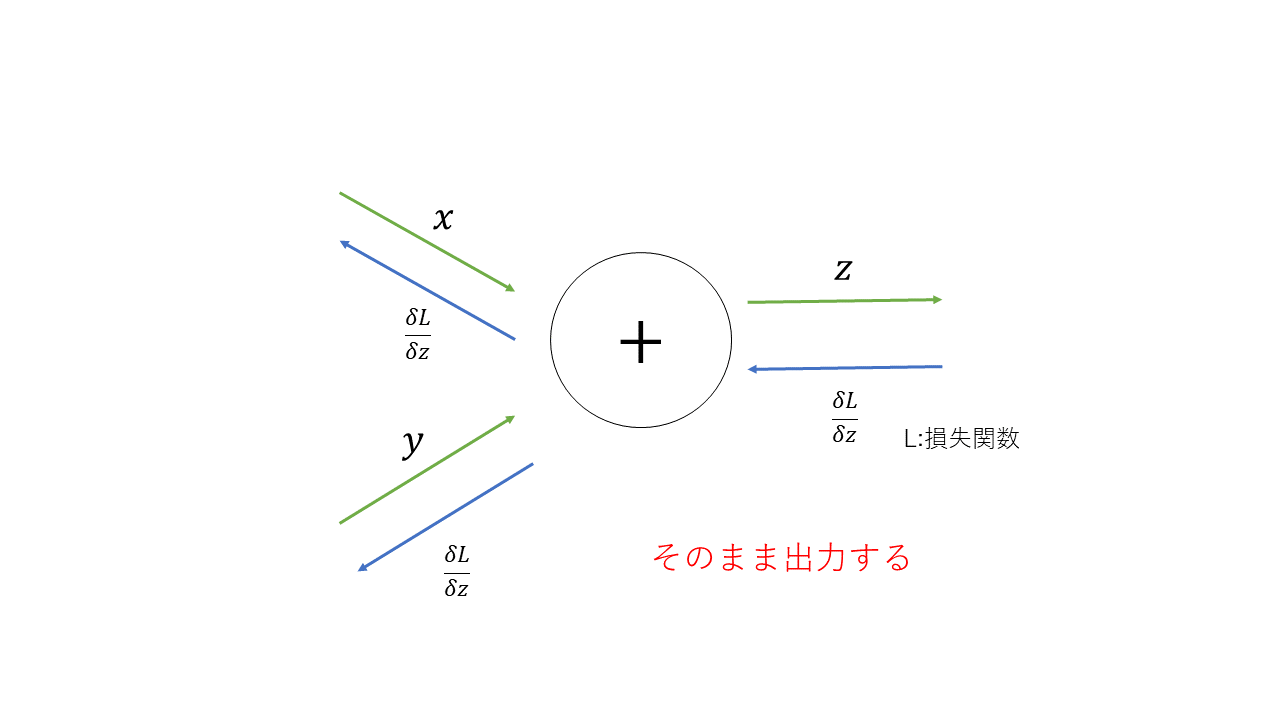
以下からは計算ノードを示しています。
→（緑）は順伝播、←（青）は逆伝播の様子です。
5.1 加算レイヤ
\begin{align}
\frac{\delta z}{\delta x}=1\\
\frac{\delta z}{\delta y}=1
\end{align}
そのまま出力する。
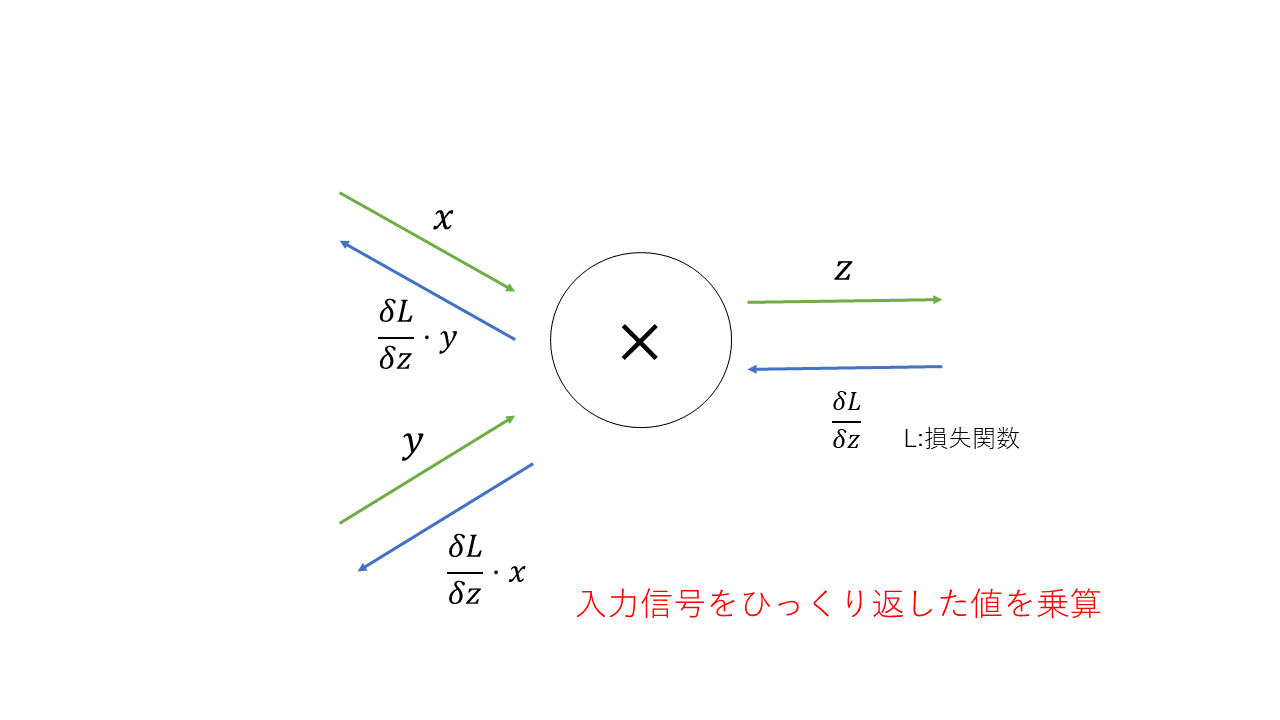
5.2 乗算レイヤ
\begin{align}
\frac{\delta z}{\delta x}=y\\
\frac{\delta z}{\delta y}=x
\end{align}
順伝播の時の入力信号の逆
5.3 ReLUレイヤ
\frac{\delta y}{\delta x}= \left\{
\begin{array}{ll}
1 & (x \gt 0) \\
0 & (x \leqq 0)
\end{array}
\right.
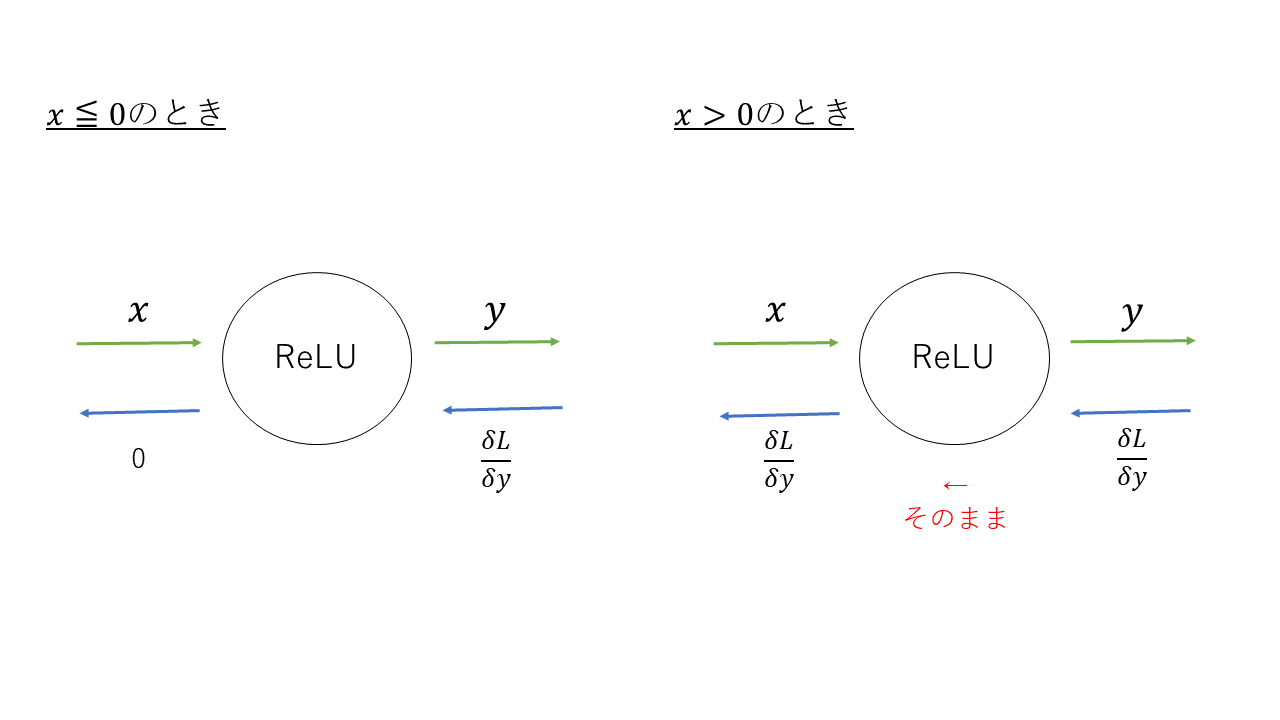
$x$は順伝播の入力のことで、
$x \leqq 0$の時は、逆伝播では下流への信号がそこでストップする。
$x > 0$の時は、逆伝播では上流の値をそのまま下流に流す。
5.4 sigmoidレイヤ
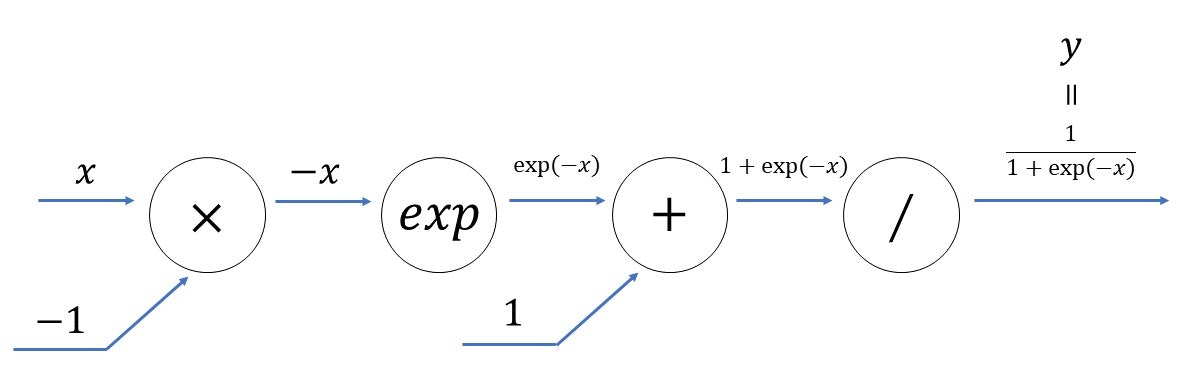
sigmoidレイヤの計算グラフ
以下は、今まで出てきていないノードの伝播の仕方。
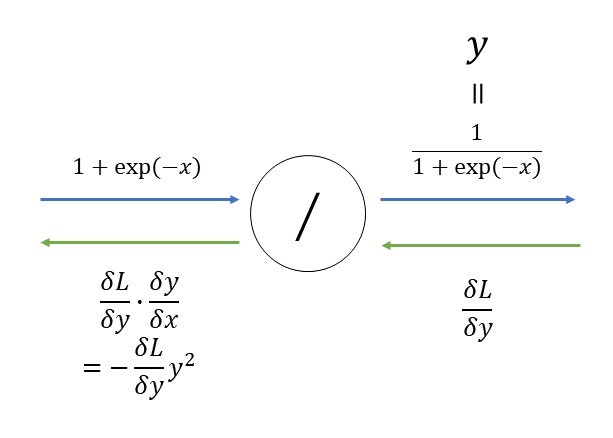
・「/」(割り算)ノード
\begin{align}
\frac{\delta y}{\delta x}&=-\frac{1}{x^2}\\
&=-y^2
\end{align}
・expノード
\begin{align}
\frac{\delta y}{\delta x}&=\exp(x)
\end{align}
最終的に
になる。
（詳しい証明は本を参照P145~）
5.5 Affineレイヤ
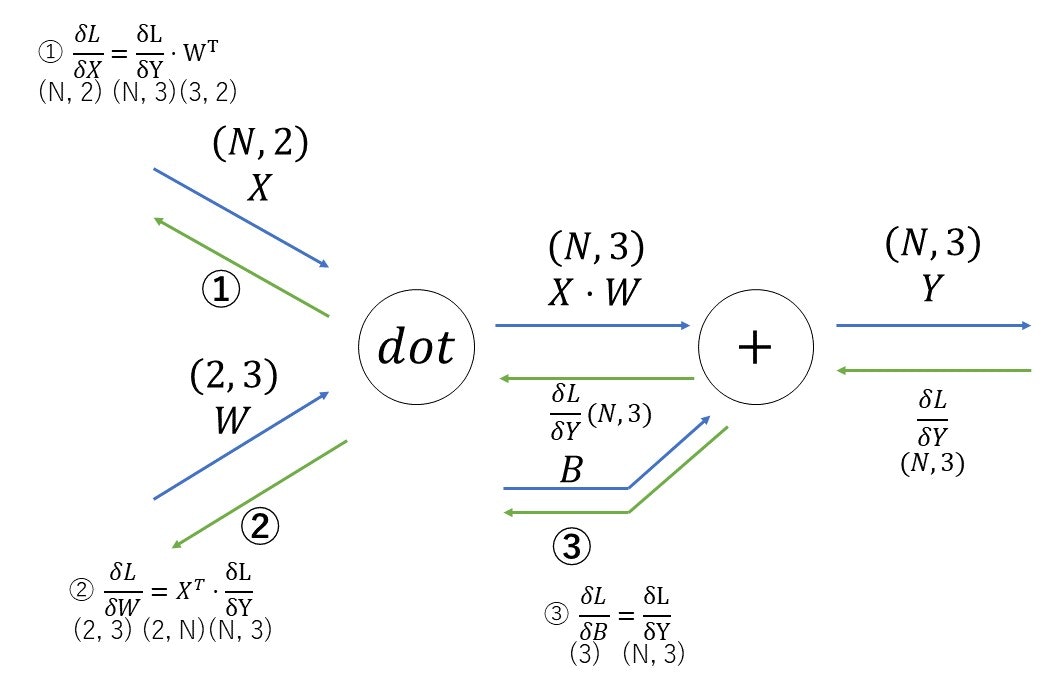
Affineレイヤの計算グラフ。
以下は、今まで出てきていないノードの伝播の仕方。
・dotノード
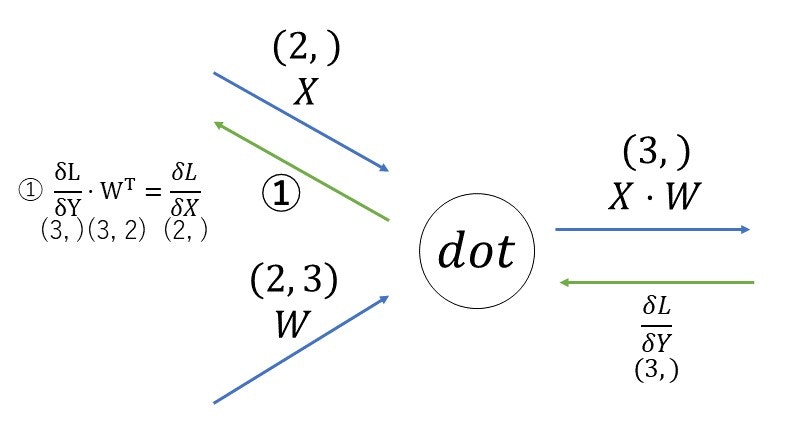
行列の対応する次元の要素数を一致させるように式を組み立てる(①)。
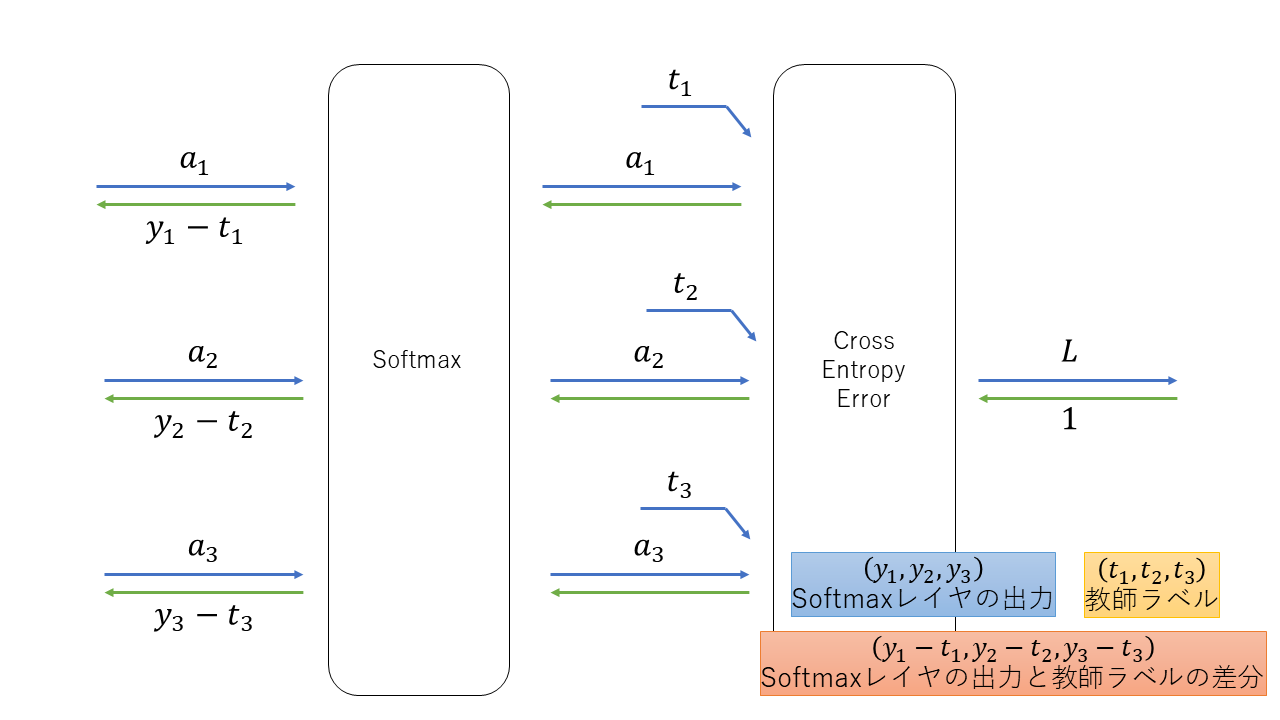
5.6 Softmax-with-Lossレイヤ
簡素化して図示すると、きれいな形になる。
##6.まとめ
他にもまとめたいことはたくさんあるのですが、全て載せると長くなってしまうので、まずつまずいたところをまとめました。
興味はある分野でしたが、勉強を始めると、プログラミングの知識以外の部分で知らない部分が多く、たくさんつまずきました。
それでも、5章のノードの部分や、7章の畳み込みニューラルネットワークなど、難しいところと同じくらい楽しいところも多く、時間をかけて勉強できてよかったなと思っています。
得た知識を活用していけるように、これからも勉強を続けて、Deep Learningに携わっていけたらなと思います。
斎藤 康毅 著
ゼロから作るDeep Learning