今年の夏頃に「ゼロから始めるMATLAB」というセミナーがありました。その時、巷で盛り上がっていたのが 「MATLABって0からじゃなくて1からでしょ」というツッコミ。
いやいや。そうとも言い切れないでしょ。
ということで、0から始まるMATLABを使ってみました。まずは、結果から見てみましょう。
x = zerobased(magic(7))
x =
7×7 zerobased:
double データ:
30 39 48 1 10 19 28
38 47 7 9 18 27 29
46 6 8 17 26 35 37
5 14 16 25 34 36 45
13 15 24 33 42 44 4
21 23 32 41 43 3 12
22 31 40 49 2 11 20
左上の値を取りだしてみると
x(0,0)
ans =
zerobased:
double データ:
30
0行目のベクトルは?
x(0,:)
ans =
1×7 zerobased:
double データ:
30 39 48 1 10 19 28
3列目の値を0に設定してみる
x(:,3) = 0
x =
7×7 zerobased:
double データ:
30 39 48 0 10 19 28
38 47 7 0 18 27 29
46 6 8 0 26 35 37
5 14 16 0 34 36 45
13 15 24 0 42 44 4
21 23 32 0 43 3 12
22 31 40 0 2 11 20
うっかり1ベースで最終行を抽出しようとすると
try
y = x(7,:)
catch ME
disp('エラー:')
disp(ME.message)
end
エラー:
位置 1 のインデックスが配列範囲を超えています (6 を超えてはならない)。
end は正しく解釈されているみたい
x(2:4,end-1)
ans =
3×1 zerobased:
double データ:
35
36
44
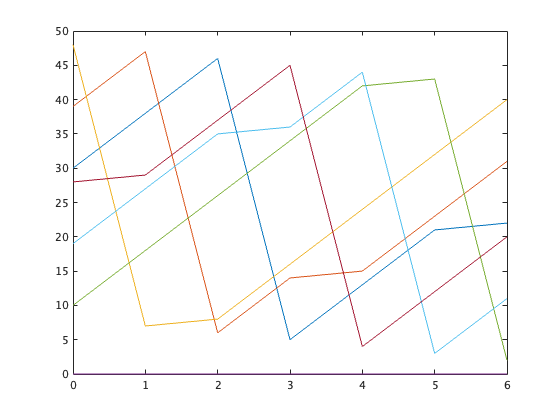
plot してみるとちゃんと横軸は0からになっている
plot(x)
演算は普通にできるみたい
a = zerobased([1 2 3 4 5])
b = zerobased([2 3 4 5 6])
c_tasu = a+b
d_kakeru = a.*b
e_bekijou = a.^b
a =
1×5 zerobased:
double データ:
1 2 3 4 5
b =
1×5 zerobased:
double データ:
2 3 4 5 6
c_tasu =
1×5 zerobased:
double データ:
3 5 7 9 11
d_kakeru =
1×5 zerobased:
double データ:
2 6 12 20 30
e_bekijou =
1×5 zerobased:
double データ:
1 8 81 1024 15625
zerobased.m の解説
さて、謎のzerobased.mを見ていきます。
サブクラス
これはオブジェクト指向で書いたクラスファイルです。また、通常の数値ベクトルとして使えるように組み込みの double型を継承しています。(ちなみに @larking95さんが「MATLAB with オブジェクト指向 への乗り換えガイド」というすばらしい記事を書いてくれたのでMATLABでのオブジェクト指向について詳しく知りたいひとは読んでみてください)
classdef zerobased < double
methods
function obj = zerobased(data)
if nargin == 0
data = [];
end
obj = obj@double(data);
end
end
end
ただ、これだけだと単に double と同じ機能を搭載するクラスを作成しただけです。
ん?いやいや。実はこれってすごいことで、double型に使えるすべての演算や関数が使えることになっています。組み込みのデータ型を拡張するために適しています。
インデックスの再定義
さて、ここからがポイントです。
1ベースインデックスから0ベースインデックスに変えるためにはインデックス付き参照(subsref)とインデックス付き代入(subsasgn)のメソッドを再定義してあげる必要があります。
subsref は
x(3,4)
と実行した時に
subsref(x,S)
という風に呼ばれます。ここで S は構造体で
S =
フィールドをもつ struct:
type: '()'
subs: {[3] [4]}
と定義されます。
ここでは、0ベースで実行されたインデックスを1ベースに変換してあげればいいのです。以下が subsref の再定義となります。
function B = subsref(A,S)
switch S(1).type
case '()'
if length(S) > 1
error('無効なインデックスです。')
end
% 0ベースインデックスを1ベースインデックスに変換
for id = 1:length(S.subs)
if isnumeric(S.subs{id})
S.subs{id} = S.subs{id}+1; % 1を足す
end
end
case '.' % 今回は対象外
error('MATLAB:structRefFromNonStruct','この型の変数ではドット インデックスはサポートされていません。')
case '{}' % 今回は対象外
error('MATLAB:cellRefFromNonCell','この型の変数では中かっこのインデックス付けはサポートされていません。')
end
end
同じく、subsasgn も再定義します。これは代入の時に呼ばれるメソッドです。
function A = subsasgn(A,S,B)
switch S(1).type
case '()'
if length(S) > 1
error('無効なインデックスです。')
end
% 0ベースインデックスを1ベースインデックスに変換
for id = 1:length(S.subs)
if isnumeric(S.subs{id})
S.subs{id} = S.subs{id}+1; % 1を足す
end
end
% 組み込みのsubsasgnを呼ぶ
A = builtin('subsasgn',A,S,B);
case '.' % 今回は対象外
error('MATLAB:structRefFromNonStruct','この型の変数ではドット インデックスはサポートされていません。')
case '{}' % 今回は対象外
error('MATLAB:cellRefFromNonCell','この型の変数では中かっこのインデックス付けはサポートされていません。')
end
end
end の再定義
これでほぼ完成です。ただ、一つ気をつけなければならないのが、end を使ったインデックスです。
x(end,:)
インデックスとして使われる end は自動的に配列のサイズを計算するので、そのままにしておくと1ベースのインデックス値に変換されてしまいます。つまり、今回の例では x(end,:) は x(7,:) として解釈されてしまい、エラーとなってしまいます。この問題を解消するために、end メソッドを再定義します。
function ind = end(obj,k,n)
szd = size(obj);
ind = szd(k)-1; % サイズから1を引く
end
演算子の再定義
組み込みデータ型を継承すると、継承されたメソッドの振る舞いが物によって異なります。特に、データの処理をする演算子などは結果(出力)をもとのデータ型(スーパークラス)として返します。例えば、x と y がともに zerobased型とすると、x+y は double型として結果が戻ってきます。これを、zerobased型として返すようにするには、演算子のメソッドをそのように再定義する必要があります。
function C = plus(A,B)
C = zerobased(builtin('plus',A,B));
end
function C = minus(A,B)
C = zerobased(builtin('minus',A,B));
end
function C = times(A,B)
C = zerobased(builtin('times',A,B));
end
function C = divide(A,B)
C = zerobased(builtin('divide',A,B));
end
function C = mtimes(A,B)
C = zerobased(builtin('mtimes',A,B));
end
function C = ldivide(A,B)
C = zerobased(builtin('ldivide',A,B));
end
function C = rdivide(A,B)
C = zerobased(builtin('rdivide',A,B));
end
function C = mldivide(A,B)
C = zerobased(builtin('mldivide',A,B));
end
function C = mrdivide(A,B)
C = zerobased(builtin('mrdivide',A,B));
end
function C = power(A,B)
C = zerobased(builtin('power',A,B));
end
function C = mpower(A,B)
C = zerobased(builtin('mpower',A,B));
end
その他メソッドの再定義
最後に、必要に応じてその他のメソッドを再定義します。ここでは plot メソッドを少し変更します。
plot(x)
としたとき、通常 x 軸は 1 から始まりますが 0 からにしてみましょう。
function varargout = plot(varargin)
if nargin == 1 % 入力引数が1つの場合のみ
data = varargin{1};
[varargout{1:nargout}] = builtin('plot',0:size(data,1)-1,data);
else
[varargout{1:nargout}] = builtin('plot',varargin{:});
end
end
zerobased クラス
`zerobased.m` の完成版です。
classdef zerobased < double
methods
function obj = zerobased(data)
if nargin == 0
data = [];
end
obj = obj@double(data);
end
function B = subsref(A,S)
switch S(1).type
case '()'
if length(S) > 1
error('無効なインデックスです。')
end
% 0ベースインデックスを1ベースインデックスに変換
for id = 1:length(S.subs)
if isnumeric(S.subs{id})
S.subs{id} = S.subs{id}+1; % 1を足す
end
end
try
% 組み込みのsubsrefを呼ぶ
B = builtin('subsref',A,S);
catch ME
% 無効なインデックスが指定された時のエラーメッセージを変更
if isequal(ME.identifier,'MATLAB:badsubscript')
nums = regexp(ME.message, '\d+', 'match');
if length(nums) == 2
% 上限の値を1少なくする
replaceTxt = num2str(str2double(nums{2})-1);
ME2 = MException(ME.identifier,regexprep(ME.message,'\d+',replaceTxt,2));
else
ME2 = ME;
end
throwAsCaller(ME2)
else
rethrow(ME)
end
end
case '.' % 今回は対象外
error('MATLAB:structRefFromNonStruct','この型の変数ではドット インデックスはサポートされていません。')
case '{}' % 今回は対象外
error('MATLAB:cellRefFromNonCell','この型の変数では中かっこのインデックス付けはサポートされていません。')
end
end
function A = subsasgn(A,S,B)
switch S(1).type
case '()'
if length(S) > 1
error('無効なインデックスです。')
end
% 0ベースインデックスを1ベースインデックスに変換
for id = 1:length(S.subs)
if isnumeric(S.subs{id})
S.subs{id} = S.subs{id}+1; % 1を足す
end
end
% 組み込みのsubsasgnを呼ぶ
A = builtin('subsasgn',A,S,B);
case '.' % 今回は対象外
error('MATLAB:structRefFromNonStruct','この型の変数ではドット インデックスはサポートされていません。')
case '{}' % 今回は対象外
error('MATLAB:cellRefFromNonCell','この型の変数では中かっこのインデックス付けはサポートされていません。')
end
end
function ind = end(obj,k,n)
szd = size(obj);
ind = szd(k)-1; % サイズから1を引く
end
function C = plus(A,B)
C = zerobased(builtin('plus',A,B));
end
function C = minus(A,B)
C = zerobased(builtin('minus',A,B));
end
function C = times(A,B)
C = zerobased(builtin('times',A,B));
end
function C = divide(A,B)
C = zerobased(builtin('divide',A,B));
end
function C = mtimes(A,B)
C = zerobased(builtin('mtimes',A,B));
end
function C = ldivide(A,B)
C = zerobased(builtin('ldivide',A,B));
end
function C = rdivide(A,B)
C = zerobased(builtin('rdivide',A,B));
end
function C = mldivide(A,B)
C = zerobased(builtin('mldivide',A,B));
end
function C = mrdivide(A,B)
C = zerobased(builtin('mrdivide',A,B));
end
function C = power(A,B)
C = zerobased(builtin('power',A,B));
end
function C = mpower(A,B)
C = zerobased(builtin('mpower',A,B));
end
function varargout = plot(varargin)
if nargin == 1 % 入力引数が1つの場合のみ
data = varargin{1};
[varargout{1:nargout}] = builtin('plot',0:size(data,1)-1,data);
else
[varargout{1:nargout}] = builtin('plot',varargin{:});
end
end
end
end
最後に
今回は、既存のクラスを継承し、subsref と subsasgn を再定義することによって0から始まるMATLABを実現しました。ただ、完璧に作り上げるにはもっとエラーチェック機能を追加したり、double型が使える全ての関数を見直して再定義するものがあるかを考える必要があると思っています。
MATLABが初めての言語である私にとってはあまり実用的ではないので、これはちょっとしたプログラミングの遊び程度だったかなと思います。