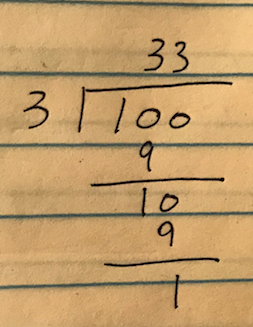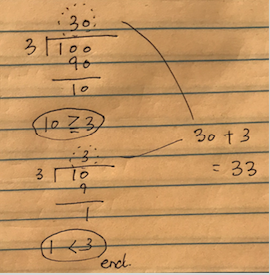はじめに
前回の高速累乗計算に続いて、シンプルなアルゴリズムに関するものです.
python3 で実装します.
ゴール
割り算(/)・掛け算(*)・剰余(%)の演算子を使わずに二つの正の整数の割り算を実装する.
ただし、整数の商のみ求め、余りは捨てる.
求まった商が
# 切り捨て除算
a // b
と同じ結果になればいいかと思います.
まず残された選択肢を検討する
単純に、四則演算をもとに考えてみましょう.
「割り算・掛け算・剰余の演算子を使わずに」ということで、
「足し算」と「引き算」が残っていることがわかります.
たとえば引き算
割り算なので被除数をどんどん小さくしていく必要があります. そういった点を考えると、引き算は都合がいいかもしれません.
以下は、除数で被除数をどんどん引いていくことを実装しています.
def division_brute_force(a, b):
"""
a // b
:param a: dividend
:param b: divisor
:return: quotient
"""
n = 0
while a >= b:
a -= b
n += 1
return n
ただし、このような力任せ方法だと、データが大きくなればなるほど、計算が遅くなってしまいます.
一例で、
2^{50} \div 1
このように被除数と除数の差が大きすぎるとき、
除数1は被除数2^50を2^50回引くことになります.
試しで値を入れてみましたが、私の環境だと、長々と返ってこないです...😉
そこで、他の演算子をも検討する必要性が出てきます.
ビット演算子です. なかでも、シフト演算子を利用します.
まずはシフト演算について、次にどう利用できるかについて考えてみます.
シフト演算
二進数のビット(桁)、つまり0と1の列をずらします.
論理シフト(符号なし)と算術シフト(符号あり)でさらにわけられます.
nビット左にずらす = 2^{n} 倍
\\
nビット右にずらす = 2^{-n} 倍
論理シフト(符号なし)
例
10進数の8は2進数で表すと1000です.
1000を3bit論理左シフト
3桁左へずらして1000_ _ _空いたところには0を埋めます.
1000000 (10進数の64)
1000を3bit論理右シフト
右から数えて3桁捨てます. ぽん.
1 (10進数の1)
算術シフト(符号あり)
算術シフトの場合は、一番左のビットが「符号」となり、0なら正の数、1なら負の数を意味します.
シフトを行う際は、符号ビットは位置を固定したまま、符号より右にあるビット列を左右にずらして計算します.
例
10進数の-16を8bitの補数表現の2進数で表すと11110000です.
これは9bitの100000000から10000を引いた結果です.
11110000を2bit算術左シフト
一番左の符号の1を固定して、残りの1110000を左に2bitずらすと、111000000になりますが、
このままだと桁があふれるので、左側から1番目と2番目を捨てて1000000にします.
あとは固定しておいた符号1とくっつけると11000000が求まります(10進数の-64)
11110000を2bit算術右シフト
一番左の符号の1を固定して、残りの1110000を右に2bitずらすと、_ _ 1110000になりますが、
このままだと桁があふれるので、右側から1番目と2番目を捨てて_ _ 11100にします.
空いた桁には符号と同じ数字を埋めるので、1を埋めると1111100になります.
あとは固定しておいた符号1とくっつけると11111100が求まります(10進数の-4)
ただ、今回は正の整数のみを限定して扱うので、論理シフトをベースに考えていきます.
演算子
# shift Left
8 << 3 # 64
# shift Right
8 >> 3 # 1
もう一度割り算
たとえばこれ.
100 \div 3
商は33、余りは1です.
余りは捨てるので、求める結果は33になります.
割り算を紙に書いて計算する時、こういう風に計算すると思います.
タイピングでは、うまく表現できず......
割り算は、被除数を除数で引いていくことで実装できる、という点を考慮すると、
被除数を
除数 \times k \times 10^{n}
で引いて小さくしていけばいいことがわかります.
10進数なのでkは1から9の間の自然数になるでしょうし、自然数nは桁になります.
割った余りが次の被除数となり、上記の式が被除数よりは大きくならない、ぎりぎりの大きさになるようにnを決めていきます.
この過程を、余り(次の被除数)が除数より小さくなるまで繰り返すことになります.
途中から出てきた商を足し合わせると、最終的な商が求まります.
普通の割り算です.
もう一度割り算 (二進数)
まったく同じ式を2進数に変換します.
1100100(2) \div 11(2)
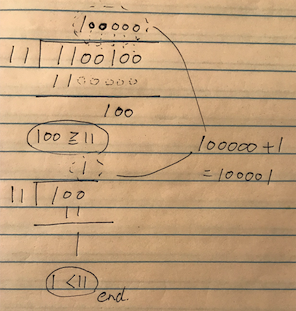
被除数を
除数 \times 2^{n}
で引いて小さくしていけばいいことがわかります.
2進数なので、先ほどのkは1となります.
下記のことを考慮すると、掛け算の演算子の代わりにシフト演算子を使うことでこの割り算が実装できることがわかります.
nビット左にずらす = 2^{n} 倍
余り(次の被除数)が除数より小さくなるまで繰り返します.
シフト演算で割り算
ゼロ除算例外処理と、除数が被除数より大きい場合の処理も含んでいます.
最初に扱うビット数を決めて、除数のビットを削っていく実装
def division_binary_shift_m(a, b, m):
"""
:param a: dividend
:param b: divisor
:param m: maximum bit capacity
:return: quotient
"""
if a < b:
return 0
if b == 0:
raise ZeroDivisionError
q = 0
sb = b << m
rem = a # remainder (init is dividend)
while rem >= b:
while sb > rem:
sb = sb >> 1
m = m - 1
q = q + (1 << m)
rem = rem - sb
return q
最初に扱うビット数mを決めて、除数のビット数を一旦最大ビットまで増やして(左シフトして)おきます.
余りremの初期値は、まだ何も引いていないので、被除数になります.
被除数で割れるようになるまで、一つずつ除数のビットを削って(右にシフトして)いきます.
除数と共にビット数mも一つずつ減らしていきます.
内側の while loop により「除数より大なりイコールな被除数」な状態(割り算できる状態)になったら、桁数mが決まります.
商qには2^mを足します. 2のm乗を1 << mで表現しています.
余りからは除数を引いて、次の被除数にします.
シフト演算子より加法(+ と -)の方が優先されるので、括弧で囲みます.
q = q + (1 << m)
複合代入(+= など)はシフト演算子より順位が低いのでまとめて書くと括弧要らず.
q += 1 << m
最大桁を決めずに、除数のビットを増やしていく実装
def division_binary_shift(a, b):
"""
a // b
:param a: dividend
:param b: divisor
:return: quotient
"""
if a < b:
return 0
if b == 0:
raise ZeroDivisionError
q = 0
sq = 1
ori_b = b
while a >= b:
b <<= 1
if a >= b:
sq <<= 1
else:
b >>= 1
a -= b
q += sq
sq = 1
b = ori_b
return q
被除数のサイズのぎりぎりまで除数(b)を左シフトしていきます.
各段階における商(sq)も、同じく桁を増やしていきます.
除数が被除数より大きくなったら除数を一つ少ない桁に戻して、被除数から除数を引きます.
各段階から出てきた商は、最終的な商(q)に足していきます.
各段階における一連の処理が終わったら(被除数から引いて、最終的な商に貯める)商を1に、除数をもともとの除数に戻します.
実行例
a, b = 14285699999999857143, 7
m = 64
expected = a // b
assert division_binary_shift_m(a, b, m) == expected
assert division_binary_shift(a, b) == expected
# 商は 2040814285714265306
メモリ使用量
せっかく(?)だから、並べて比較してみました.
一応、一番最初の brute_force 版もかけてみましたけど、案の定まったく返ってこない 😉
$ python -m memory_profiler my_division.py
Filename: my_division.py
Line # Mem usage Increment Line Contents
================================================
4 26.395 MiB 26.395 MiB @profile
5 def division_binary_shift(a, b):
6 26.395 MiB 0.000 MiB if a < b:
7 return 0
8 26.395 MiB 0.000 MiB if b == 0:
9 raise ZeroDivisionError
10
11 26.395 MiB 0.000 MiB q = 0
12 26.395 MiB 0.000 MiB sq = 1
13 26.395 MiB 0.000 MiB ori_b = b
14 26.398 MiB 0.000 MiB while a >= b:
15 26.398 MiB 0.000 MiB b <<= 1
16 26.398 MiB 0.004 MiB if a >= b:
17 26.398 MiB 0.000 MiB sq <<= 1
18 else:
19 26.398 MiB 0.000 MiB b >>= 1
20 26.398 MiB 0.000 MiB a -= b
21 26.398 MiB 0.000 MiB q += sq
22 26.398 MiB 0.000 MiB sq = 1
23 26.398 MiB 0.000 MiB b = ori_b
24
25 26.398 MiB 0.000 MiB return q
Line # Mem usage Increment Line Contents
================================================
28 26.402 MiB 26.402 MiB @profile
29 def division_binary_shift_m(a, b, m):
30 26.402 MiB 0.000 MiB if a < b:
31 return 0
32 26.402 MiB 0.000 MiB if b == 0:
33 raise ZeroDivisionError
34
35 26.402 MiB 0.000 MiB q = 0
36 26.402 MiB 0.000 MiB sb = b << m
37 26.402 MiB 0.000 MiB rem = a
38 26.402 MiB 0.000 MiB while rem >= b:
39 26.402 MiB 0.000 MiB while sb > rem:
40 26.402 MiB 0.000 MiB sb = sb >> 1
41 26.402 MiB 0.000 MiB m = m - 1
42
43 26.402 MiB 0.000 MiB q = q + (1 << m)
44 26.402 MiB 0.000 MiB rem = rem - sb
45
46 26.402 MiB 0.000 MiB return q
おわりまして
コンピューターが行う掛け算と割り算は、ビットを左右にずらすことがベースになっていると思いますが、改めてそういった演算や実装に関して考えるきっかけになって、興味深かったです.
ご指摘や補足などありましたら、随時教えてくださいませ.