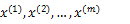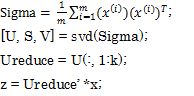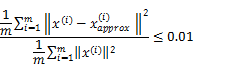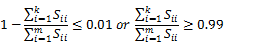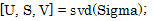機械学習用語としての「次元削減(Dimensionality Reduction)」について、「次元削減という言葉を初めて聞いた」という程度の方を対象に、次元削減の目的・方法から、どんな方法で実現するのかという話までを説明する記事です。
なお、いろいろと日本語訳にブレがあるようですが、「次元削減」で通します。
本記事は、courseraで提供されているAndrew Ng氏の機械学習講義の内容を参考に、「次元削減」に関して説明するものです。
また、本記事では、「次元削減」の手法として、主成分分析(PCA:Principal Component Analysis)を取り上げます。
次元削減
次元削減とは?
「次元削減」とは、文字通り、データの次元数を減らすことです。
ここでいう「次元数」は、データセットのフィーチャーの数と言い換えることができます。
以下に次元削減の例を示します。

上図上は身長と体重の関係を示したグラフです。
このグラフにおいて、プロットされている×は体格を示したもので、右上方向に進むほど、体格が良いととらえることができます。
それを一次元の線上に落とし込んだものが上図下の赤い直線になります。
この状態でも、右へ進むほど体格が良くなっている、と認識することができるかと思います。
今回の例は、二次元から一次元に落とし込んでいますが、削減後も体格を示すというデータの意味を保つことができています。
この場合、赤い直線は「体格」の軸と呼ぶことができるでしょう。
次元削減とは、多次元からなる情報を、その意味を保ったまま、それより少ない次元の情報に落とし込むことです。
例えば、こんな場合に次元削減
次元削減を行う目的は主に以下の二つです。
- データの圧縮
- データの可視化
データの圧縮
データの圧縮について、単純に2次元の情報を1次元に落とし込むことができれば、それは情報が圧縮出来ている、といえるでしょう。
つまり、二次元情報
(x, y)
を、一次元情報
(z)
に落とし込むわけです。
データセットが膨大になりやすい機械学習の分野において、このデータの圧縮は計算資源の有効活用という点について、非常に有用です。
なにせ、xとyの二つについて計算を行っていたところをz一つに対する計算で済ませることができるわけですから、単純に、高速に計算を行うことができるようになります。
加えていえば、上の例は2次元→1次元でしたが、実際には10000次元→1000次元という規模の圧縮も現実的なレベルなのですから、次元削減の有無による効率の差は言うまでもないでしょう。
ただし、圧縮により元のデータが少なからず損失している点には注意が必要です。
データの可視化
次にデータの可視化について、例えば世界各国の統計データには、
- データセット名:日本、アメリカ、カナダ、イギリス、フランス、中国、ドイツ、…
- フィーチャー:GDP、人口、面積、領海、経済水域、輸出入額、…
といった情報が含まれるでしょう。
その情報はいずれも有益ですが、一度に提示することは難しいです。
少なくとも、4次元以上の情報を端的に表現することは難しいと言わざるを得ません。
そこで行うのが「次元削減」です。
各国のデータに対して、二次元まで次元削減を行ったという前提で、以下の画像を見てみましょう。

一つの×は一つの国を表します。
ここでは軸名は指定しません。
二次元のグラフであるという前提の上で、なんとなくで構いませんが、右上の×(=国)は「良く」、左下の国は「悪い」と認識できるでしょうか?
この、「認識できる」というのが重要です。
多数の次元・フィーチャーからなるデータセットというのは珍しくありませんが、人間が効率的に可視化可能な次元数というのは、二次元か三次元といった程度です。
しかし、逆を言えば、そこまで落とし込むことができれば、視覚的にわかりやすく情報を提示することができるということでもあります。
その点について、可視化を目的に情報の次元を削減することは、非常に良い手段であるといえます。
この場合のデメリットは、データの圧縮を目的とした場合よりも、概ね多くの次元を削減しているということでしょう。
例えば、上で取り上げている身長と体重の例においては、削減後得られる情報は「このデータ(被験者)は体格が良い(or悪い)」といったレベルのもので、身長・体重といった元の具体的なデータはわからなくなります。
視覚的には認識しやすくなりますが、あくまで「そういった傾向がある」程度の精度に落ちてしまうため、厳密な情報とは言えなくなる点には注意が必要です。
次元削減の手法
主成分分析(PCA)の概要
ここまで、次元削減の目的について触れてきましたが、ここからは具体的な手法であったり、基準であったりといった部分に触れていきます。
次元削減を実現する際には、主成分分析(PCA:Principal Component Analysis、以下PCA)と呼ばれる手法が良く使われています。
PCAは、重みを付けたうえで多数のフィーチャーを統合し、少数の新たなフィーチャーを作り出すものです。
PCAは、集団を最もよく表現するベクトル上にデータを射影するすることで、フィーチャーを統合し、新しい指標としています。
その結果として、データ全体としての意味を保ちつつ、次元を削減することが可能となります。
射影先のベクトルを求める作業において、「集団を最もよく表現するベクトル」とは、下図中の青い線分の長さの二乗和を最小化するもののことを指します。

この青い線分は射影先のベクトルと各データの間の距離を示したもので、似たような図を用いる線形回帰とは異なり、線分(または平面など)に垂直になります。
その長さは「射影誤差」、または青い線分の長さだけ、二次元情報が欠落する故に、「情報損失量」とも呼ばれます。
この誤差・損失量が小さいほど、それぞれのデータをよく保持しているといえます。
概念として、上図は二次元を一次元に削減する図ですが、三次元を二次元に落とし込む場合には、直線ではなく、平面に対して射影誤差を求めるという風に変わるだけです。
PCAにおいて射影先の直線(上図赤い直線)は、「データのばらつきの大きい方向」を求めることで得ることができます。
この**「ばらつき」は「分散」**と言い換えることもでき、PCAは、最も分散の大きい方向を指すベクトルを得ることを目指します。
上記図中のすべての方向について分散を計算すると、赤い直線の方向(またはその逆方向)が、もっともデータの分散が大きい方向であるはずです。
主成分分析(PCA)のアルゴリズム
このフィーチャーの射影先を求める手順として、n次元をk次元に削減する場合、データセットを
としたとき、PCAのアルゴリズムは、
- 共分散行列Σを求める
- 共分散行列の固有値λと固有ベクトルxを求める
- M個の固有ベクトルを並べた行列を作る
- データから、3.の平均ベクトルを引く
- データを固有ベクトルを並べた行列を使用して変換し、射影データzを求める
という風になります。
共分散は、二組の対応するデータの平均からの偏差の積の平均値です。
分散が最大となる方向は、数学的には共分散行列の固有値と固有ベクトルに対応します。
なので、固有値、固有ベクトルを得た段階で、もっともそれらしい射影先のベクトルを得ることができていることになります。
あとは、その射影先のベクトルに従って、各々のデータを射影していくだけです。
また、これを特異値分解(SVD:Singular Value Decomposition)を関数として呼び出せる場合に、コードとして具体化すると、以下のようになります。
特異値分解によって得た固有ベクトルの行列Uから、対象を抜き出します。
そして、抜き出した行列を使用して元データxを変換し、射影後の行列zを取得します。
次元数の決定
次元削減の手順について説明しましたが、次元削減を行う際に、恐らく最も重要な要素は「どれだけの次元数を削減するか」という点でしょう。
これは射影先のデータをXapproxと置き、以下の式を用いて判定できます。
式は、共分散を用いて、以下のように書き換えることもできます。
ここでSiiは共分散を示します。
共分散Sは、特異値分解を関数として利用すると、
の左辺S中の対角行列として得ることができます。
上記の不等式を満たしている場合、その主成分の数kについて行ったPCAは、分散の99%の成分を保持していることを示します。
この保持する成分の割合が高いほど、次元削減前の元データの分散、つまり広がりを保持できているということになります。
この「分散の保持」について、以下に例を示します。

緑の直線は元のデータを良く保持できていない結果です。
この場合、この緑の直線に従って主成分分析を行った結果、保持されている分散は、最大と思われる方向に比べ、小さくなります。
例えば左下、あるいは右上のデータからは、非常に多くの情報が欠落してしまう状態です。
つまり、それだけの量の情報を損失しているということで、良い射影先とは言えません。
対して、赤い直線はデータの分散をよく保持しているといえます。
分散が保持できている割合が高ければ、それだけ情報の損失も小さく抑えることができるといえるでしょう。
ただし、比較対象は、どの程度の正確性を求めるかによって、変えてください。
他には0.05(=95%)辺りが良く使われます(目的・求める精度による)。
まとめ
次元削減は、
- データの圧縮
- データの可視化
を目的に、データの次元数を削減するものです。
実際に、次元削減を行う際には基本的に、
- PCAを実行してみる。
- その結果が基準を満たしているかどうか判定する。
- 満たしていなければ条件を変えて再度実行してみる。
というのが流れを満足行くまで繰り返すことになります。
データの可視化を目的とするのならば、そこまで悩む必要なしに、二次元or三次元まで次元削減を実行してください。
データの圧縮を目的とするのであれば、削減数のチェックを踏まえつつ、次元削減を行ってみてください。