1. 概要
* その2( https://qiita.com/asys/items/622594cb482e01411632 )に引き続き『経済・ファイナンスデータの計量時系列分析』を元に勉強中。
* 今回は3章に当たる部分、AR,MA,ARMAを用いた予測について。
2. データ
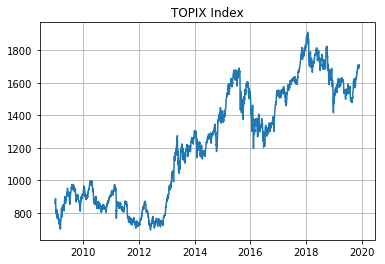
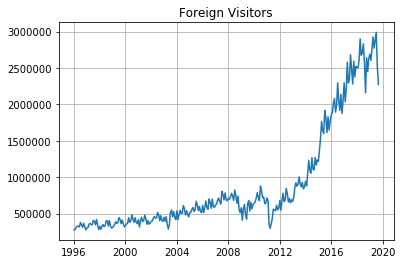
前回に引き続きTOPIXのヒストリカルデータと月次訪日外客数のデータを使用する。
3. AR過程の予測
以下予測をするにあたって、平均2乗誤差(MSE)を最小にする予測を最適予測とする。
$AR(p):\quad y_t=c+\phi_1y_{t-1}+\phi_2y_{t-2}+\cdots+\phi_py_{t-p}+\epsilon_t,\quad \epsilon_t\sim W.N.(\sigma^2)$
AR過程の予測にあたっては以下の性質を用いての逐次予測のアプローチが一般的である。
$\left\{\begin{array}{ll} E(y_\tau|\Omega_t)=y_\tau,&\tau\leq t \\E(\epsilon_{t+k}|\Omega_t)=0,&k>0\end{array}\right.$
ただし、$\Omega_t=\{y_t,y_{t-1},\cdots,y_1\}$
この時、最適1期先予測は、
$\hat y_{t+1|t}=c+\phi_1y_t+\phi_2y_{t-1}+\cdots+\phi_py_{t-p+1}$
となり、MSEは
$MSE(\hat y_{t+1|t})=E(\epsilon_{t+1}^2)=\sigma^2$
となる。
次に最適2期先予測は、
$\begin{split}\hat y_{t+2|t}&=c+\phi_1\hat y_{t+1|t}+\phi_2y_t+\cdots+\phi_py_{t-p+2}+\epsilon_{t+2}\\ &=(1+\phi_1)c+(\phi_1^2+\phi_2)y_t+(\phi_1\phi_2+\phi_3)y_{t-1}+\cdots\phi_1\phi_py_{t-p+1}\end{split}$
となり、この時MSEは
$MSE(\hat y_{t+2|t})=E(\epsilon_{t+2}+\phi_1\epsilon_{t+1})^2=(1+\phi_1^2)\sigma^2$
となる。
このように逐次的にh期先予測を求めていく。
以上がAR過程の点予測であるが、区間予測については以下のようになる。
仮に1期先の95%区間予測を考えてみる。
$y\sim N(\mu,\sigma^2)$の時、
$P(-1.96\leq\frac{y-\mu}{\sigma}\leq1.96)=0.95$
$P(\mu-1.96\sigma\leq y\leq\mu+1.96\sigma)=0.95$
が成り立つ。ここで、$y_{t+1}$の条件付き分布は
$N(\hat y_{t+1|t},MSE(\hat{y}_{t+1|t}))$
となるので、1期先の95%区間予測は、
$\bigl( \hat y_{t+1|t}-1.96\sqrt{MSE(\hat y_{t+1|t})},; \hat y_{t+1|t}+1.96\sqrt{MSE(\hat{y}_{t+1|t})}\bigr)$
となる。
一般に$AR(p)$のh期先MSEを求めることは難しく、シミュレーションで近似する手法などが使われる。
4. MA過程の予測
無限個の観測値がある場合、反転可能なMA過程は
$y_t = \sum_{k=1}^{\infty}\eta_ky_{t-k}+\epsilon_t$
と、$AR(\infty)$に書き直すことができるため、$MA(q)$の最適予測は、
(1)$q$期までの最適予測は全ての観測値$\Omega_t$に依存する。
(2)$q+1$期先以上の予測は単に過程の期待値に等しい。
(3)$q+1$期先以上の予測はのMSEは過程の分散に等しい。
という性質を持つ。
他方、有限個の観測値しかない場合も、$q$期先以上の予測は過程の期待値となり、MSEは過程の分散となる。$q$期までの予測については標本期間以前の$\epsilon=0$を仮定して予測を行うことが一般的である。
5. ARMA過程の予測
ARMA過程の予測はAR過程とMA過程の予測を組み合わせたものである。
以下、その2( https://qiita.com/asys/items/622594cb482e01411632 )でも使用した訪日外客数のデータを用いてARMA過程の予測を行ってみる。
その2で$p=4,q=1$がよさそうということがわかっているのでそれを利用する。
今回は全データ138個のうち、最初の100個をモデル構築に使用し、残りの38個を予測しにいく。
以下のようにpredictの機能を使うことで簡単に予測を得ることができる。
arma_model = sm.tsa.ARMA(v['residual'].dropna().values[:100], order=(4,1))
result = arma_model.fit()
pred = result.predict(start=0,end=138)
arma_model = sm.tsa.ARMA(v['residual'].dropna().values[:100], order=(4,1))
result = arma_model.fit()
pred = result.predict(start=0,end=138)
pred[:100] = np.nan
plt.figure(figsize=(10,4))
plt.plot(v['residual'].dropna().values, label='residual')
plt.plot(result.fittedvalues, label='ARMA(4,1)')
plt.plot(pred, label='ARMA(4,1) pred', linestyle='dashed', color='magenta')
plt.legend()
plt.grid()
plt.title('ARMA(4,1) prediction')
plt.show()
予測はAR過程とMA過程を合わせたものであり、予測する期間が長くなるほど精度が落ちていくのは直感的な理解と整合性がある。一方で1期先や2期先の予測精度は悪くない。どのように予測を使うかはその目的によって大きく異なるだろうが、例えば株式市場では月次訪日外客数の数字によってその後のインバウンド銘柄の値動きが影響を受けるため、公表前に数字を予測してポジションを取るといった活用が考えられる。この場合必要なのは1期先の予測のみであり、1期先の予測の精度にのみ関心がある。
そこで、1期先の予測精度を調べてみると、
res_arr = []
for i in range(70,138):
arma_model = sm.tsa.ARMA(v['residual'].dropna().values[:i], order=(4,1))
result = arma_model.fit()
pred = result.predict(i)[0]
res_arr.append([v['residual'].dropna().values[i], pred])
res_arr = np.array(res_arr)
sns.regplot(x=res_arr[:,0], y=res_arr[:,1])
plt.xlabel('observed')
plt.ylabel('predicted')
plt.show()
ということで、正の相関はあるもののばらつきも大きく、ちょっと実戦投入はためらわれるレベルである。


