PCを使ってオーディオ測定用のテスト信号を作っていきます。
そんなの簡単じゃないかと思うかもしれませんが私には手強かったです。
試行錯誤したことをそのまま書いたのでまとまりがありません。
書いてる人
エンジニアではありません(Qiitaの定義ではなく世間一般的な意味で)。
ただのオーディオマニアです。
数値計算もプログラミングも素人なので見当ハズレのことを書いてる可能性があります。
もちろんNimにも詳しくありません。
変なところがあったら指摘してください。
オーディオ測定用テスト信号を作ろう!
オーディオをやっていると測定用の信号が欲しいときがあります。
20Hzからの1/3oct刻みの正弦波、対数スイープ信号、ホワイトノイズ、ピンクノイズ、M系列疑似ノイズなど。
昔は(今もか?)テスト信号のCDなどで売られていましたが、パソコンを使って簡単に音声ファイルを作ることができます。
サンプリング周波数44.1kHzだけでなくてハイレゾのファイルでも自由自在なので作っていきます。
試した環境
- Ubuntu22.04 amd64
- nim 1.6.14
- sox v14.4.2
- Gnu Octave 6.4.0
グラフの作成にはGnu Octaveを使ってます。
作成するプログラム
今回作る信号は2つです。
- サンプリング周波数、持続時間、周波数を指定して正弦波の信号を作る。
- サンプリング周波数、持続時間、開始周波数、終了周波数を指定してログスイープ信号を作る。
正弦波は周波数がサンプリング周波数(fs)の整数分の1、とくにfs/4のときは作るのが簡単で測定によく使われます。
ログスイープはインパルス応答の測定でよく使われます。
時間による周波数変化が指数関数となります。
ハイレゾの サンプリング周波数96kHz 32bit wavファイルで出力することにします。
wavファイルを作るのは面倒なので、 音声信号処理プログラミングのスイスアーミーナイフとよばれるsoxを使います。
sox単体でテスト信号を出力することができますがそこは考えない。
作るプログラムは倍精度浮動小数点を出力することにして、pipeでsoxにデータを渡します。
普通に作る
プログラミング言語には何を使ってもあまり変わらないと思いますが、Nimを使ってみます。
Python風にインデントでプロックを作っていく言語です。
C言語に変換した後にコンパイルされるので速度が速いです。
倍精度浮動小数点(float64)で計算して標準出力に書き出します。
float64のデータを32bit wavファイルに変換するのに外部プログラムのsoxを使用します。
正弦波
まずは基本の正弦波です。 計算式は
y = sin(t * f * 2π)
そのまま計算します。
tone0.nim
import std/math
func mkTone0*(fs, duration, f: float): seq[float64] =
var s = newSeq[float64]((fs*duration).int)
for n in 1..<(fs*duration).int:
s[n] = sin(n.float/fs * f * 2 * Pi)
return s
#=================
when isMainModule:
import cligen
proc tone0(fs, duration, f: float): int =
if f >= fs/2:
stderr.writeLine("ERROR! f >= fs/2")
return 1
var s = mkTone0(fs, duration, f)
discard stdout.writeBuffer(s[0].addr, sizeof(s[0])*len(s))
dispatch tone0
実行ファイルを作ります
nim c -d:release tone0.nim
32bit wavファイルに変換するのに外部プログラムのsoxを使います。
サンプリング周波数96kHzで40001Hz 120秒のモノラル信号を32bit wav
で作る
./tone0 --fs 96000 -d 120 -f 40001 | sox -t raw -e float -b 64 -r 96000 - -r 96000 -e s -b 32 t0.wav
これで120秒のwavファイルが出力されます。
可聴周波数外・フルスケールの凶悪な信号です。 再生するとスピーカーを破損したり耳に悪影響が出る可能性があります。
ログスイープ信号
charp関数なんて便利なものがあるプログラミング言語もありますが自力で計算していきます。
周波数が指数的に変化していけばよいので 時間0での周波数をf0、時間t1での周波数f1 とすれば 時間tの周波数は
f(t) = (f1/f0)^(t/t1) * f0
周波数*2πが角速度になるので積分すれば角度がでる。
この関数は簡単に積分可能なので普通に積分する。
θ = (f1/f0)^(t/t1) / log(f1/f0) * t1 * f0 * 2π + C
このままでも良いけど時間0での角度をゼロにしたいのでf0の時の角度を引いて定積分にする。
NimではC言語と違って自然対数はlog()ではなくてln()です。
logsweep0.nim
import std/math
func mkLogsweep0*(fs: float, duration: float, f0: float, f1: float): seq[float64] =
func integr(t: float): float =
pow(f1/f0, t/duration) / ln(f1/f0) * f0 * duration
var s = newSeq[float64]((fs*duration).int)
let angle0 = integr(0)
for n in 1..<(fs*duration).int:
var angle1 = integr(n.float/fs)
s[n] = sin((angle1 - angle0)*2*Pi)
return s
#============================================================
when isMainModule:
import cligen
proc logsweep0(fs,duration,f0,f1: float): int =
if (f0 >= fs/2) or (f1 >= fs/2):
stderr.writeLine("freq >= fs/2 !!")
return 1
var s = mkLogsweep0(fs, duration, f0, f1)
discard stdout.writeBuffer(s[0].addr, sizeof(s[0])*len(s))
dispatch logsweep0
同様に実行ファイルを作ってSoxで32bit wavファイルに変換します。
nim c -d:release logsweep0.nim
サンプリング周波数96kHzで120秒、 20Hzから45kHzのログスイープ信号を32bit wav で作る。
./logsweep0 --fs 96000 -d 120 --f0 20 --f1 45000 | sox -t raw -e float -b 64 -r 96000 - -r 96000 -e s -b 32 log0.wav
可聴周波数外を含むフルスケールの凶悪な信号です。 再生するとスピーカーを破損したり耳に悪影響が出る可能性があります。
精度はでてるか?
一見問題なさそうだし、世の中のテスト信号を作るプログラムは大抵こんなものです。
では作った信号の特性を見てみます。
正弦波の特性
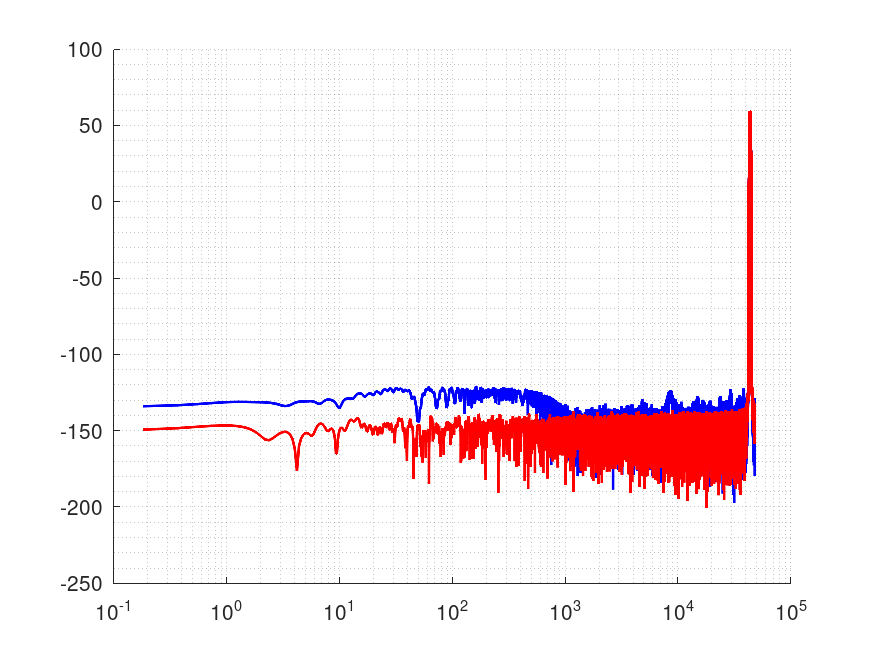
Gnu Octaveを使って120秒のテスト信号の最初の1秒と最後の1秒をfftして周波数特性を表示します。
β値20のカイザー窓を使ってます
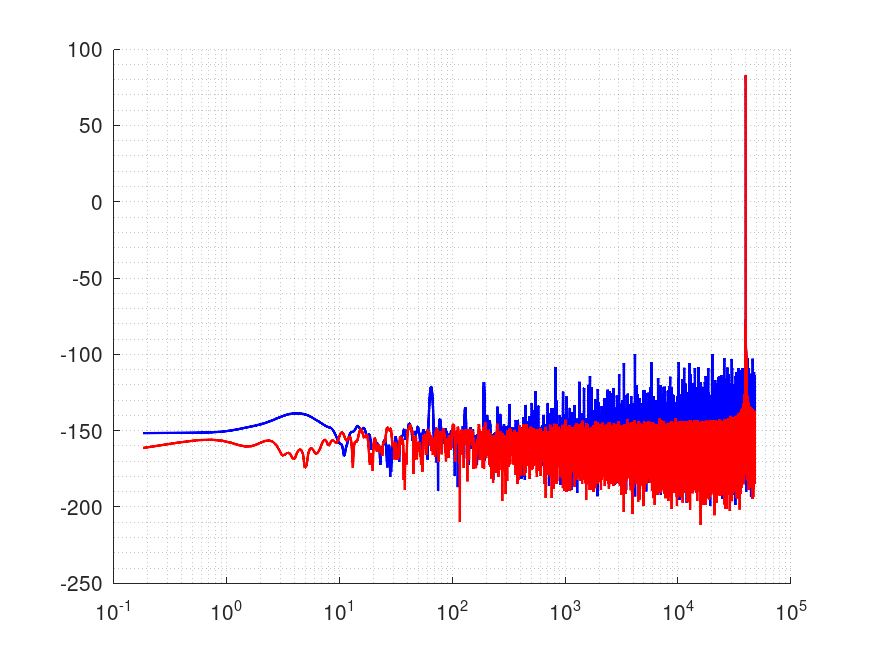
Fig.01 赤が最初の1秒、青が最後の1秒です。
ご覧のように青のほうが特性が悪くなってます。
ログスイープの特性
120秒のログスイープ信号、20Hz-45000Hzの最後の1秒と45000Hz-20Hzの最初の1秒を比較します。
Fig.02 赤が最初の1秒、青が最後の1秒です。
やはり最後の方で特性が悪化しています。
原因
浮動小数点の誤差が原因です。
64bit浮動小数点の仮数部は52bitあります。
最終出力が32bit符号付き整数なので十分な精度がありそうですが足りないのです。
正弦波40001Hzでは120秒後のsin関数の入力は倍精度浮動小数点では
(120-1/96000)*38400*2*π = 28952915.38220941
となっています。
小数点以下は8桁しかありません。
sinは2π毎の繰り返しなので有効数字の桁数が大きくても小数点以下の桁数が少ないと誤差がでてしまいます。
ログスイープでも同様に誤差が大きくなっています。
この誤差は24bit出力にすればほぼわかりません。
実用上は問題になることは少ないと考えます。
しかし最近の高性能DACは32bit入力のものもあります。
パソコンで作ったテスト信号の精度が32bit無いのはなんとなくイヤです。
というわけでこの誤差を改善する方法を考えていきます。
浮動小数点で誤差が出るなら浮動小数点を使わなければ良いじゃないか(ボツ案)
誤差の原因は浮動小数点
浮動小数点は近似値です。誤差は避けられません。
ならば浮動小数点を使わなければよいのでは?
Gnu Octave の symbolic package
Gnu Octave では symbolic package をインストールすることによって浮動小数点を使わないで記号は記号のまま計算できます。
インストール
試した環境
- OS Ubuntu22.04
Gnu Octave インストール
古いバージョンになるけど apt でインストールする。
sudo apt install octave octave-signal
version 6.4.0 がインストールされた
symbolic package インストール
octave の symbolic package は python のsympy パッケージを使っているのでインストールする。
sudo apt install python3-pip
pip install sympy
pip 22.0.2 と sympy-1.12 がインストールされた
octaveのコンソールから symbolic package をインストールする
> pkg install -forge symbolic
octsympy 3.1.1 (2023-03-19) がインストールされた
使う前にはoctaveのコンソールでloadする
> pkg load symbolic
使い方
> format long #表示桁数を増やす
> p1 = pi #倍精度浮動小数点
p1 = 3.141592653589793
> p2 = sym(pi) #pi は記号のまま
p2 = (sym) π
> x1 = sin(p1 * 10000000) #浮動小数点なので誤差が出る
x1 = 5.620555424855643e-10
> x2 = sin(p2 * 10000000) #記号のまま計算
x2 = (sym) 0
> a = sym(1.000001) # 1.000001 は浮動小数点。 symbolic に変換すると警告が出る。 値は不正確
warning: passing floating-point values to sym is dangerous, see "help sym"
warning: called from
double_to_sym_heuristic at line 50 column 7
sym at line 379 column 13
a = (sym)
2592⋅π
──────
8143
> a = sym("1.000001") # 文字列で入力すればOK
a = (sym)
1000001
───────
1000000
> c = sqrt(sym(2))
c = (sym) √2
> vpa(c) # symbolic変数を32桁表示
ans = (sym) 1.4142135623730950488016887242097
> vpa(c,200) # symbolic変数を200桁表示
ans = (sym)
1.4142135623730950488016887242096980785696718753769480731766797379907324784621070388503875343276415727350138462309122970249248360558507372126441214970999358314132226659275
055927557999505011527820605715
> double(c) # symbolic変数を倍精度浮動小数点に変換
ans = 1.414213562373095
正弦波を計算してみる
symbolic で計算して最後に倍精度浮動小数点に変換します。
tone1.m
function s = tone1(fs, duration, f)
pkg load symbolic
s = zeros(floor(fs*duration),1);
x = sym(0);
for n = 0:(fs*duration - 1)
s(n+1) = double(sin(x * f * 2 * sym(pi)));
x = x + 1/sym(fs);
endfor
endfunction
実行したところ、1/100秒(960サンプル)計算するのに180秒以上かかりました。 (Core™ i5-1135G7のノートパソコン、ネット見ながらなので不正確)
120秒のデータを作るのに25日間!かかることになります。
というわけでこの案はボツ!
別の方法を考えていきます。
積分するのをやめれば良いんじゃない?
浮動小数点が原因なのだけど、直接的にはsin関数への入力が大きな値になっているのが良くないです。
なぜ大きな値になるかというと積分してるから。
周波数の式から時間0から時間tまでの面積を求めて、2π倍すればその時間の角度になります。
そこで積分するのをやめて、区分求積法で角度を計算したら良いのでは?
1つ前のサンプル(1/fs秒前)の周波数と現在の周波数から面積を求め、1つ前の面積に足す。
サンプリング定理により周波数の最大値はfs/2より小さいので1/fs秒の区間の面積は1/2より小さくなります。
面積の2倍が1を超える毎に2を引いて小数点以下の桁数を保つようにします。
最後にπを乗じれば精度を保った角度が得られる(はず)。
正弦波
周波数一定の正弦波は角速度が一定なので簡単です。
角度が前のサンプルよりもf/fs*2π増えます。
πも浮動小数点では近似値なので使う回数を少なくするために最後に掛けることにします。
tone1.nim
# sin wave Riemann sum
import std/math
func mkTone1*(fs, duration, f: float): seq[float64] =
var
s = newSeq[float64]((fs*duration).int)
w: float #radian/Pi
w1: float = 1/fs * f * 2 #1/fs sec, radian/Pi
for n in 1..<(fs*duration).int:
w = w + w1
if w > 1:
w = w - 2
s[n] = sin(w * Pi)
return s
#=================
when isMainModule:
import cligen
proc tone1(fs, duration, f: float): int =
if f >= fs/2:
stderr.writeLine("ERROR! f >= fs/2")
return 1
var s = mkTone1(fs, duration, f)
discard stdout.writeBuffer(s[0].addr, sizeof(s[0])*len(s))
dispatch tone1
ログスイープ
正弦波は周波数が一定=角速度が一定なので区分求積法で誤差が出ません。
しかしログスイープは時間によって周波数が変化し、その周波数変化も直線的ではありません。
周波数変化が直線なら台形法で誤差が出ないけど曲線なので2次関数で近似したほうが良さそうです。
というわけでシンプソン法で計算してみます。
logsweep1.nim
# logsweep Simpson's rule
import std/math
func mkLogsweep1*(fs: float, duration: float, f0: float, f1: float): seq[float64] =
func freq(t: float): float =
return pow(f1/f0, t/duration) * f0
var
s = newSeq[float64]((fs*duration).int)
fr0 = f0
w: float = 0 # radian/Pi
for n in 1..<(fs*duration).int:
var fr2 = freq(n.float/fs)
var fr1 = freq((n.float - 0.5)/fs)
w = w + (fr0 + fr1*4 + fr2)/fs/6*2
if w > 1:
w = w - 2
s[n] = sin(w * Pi)
fr0 = fr2
return s
#=================
when isMainModule:
import cligen
proc logsweep1(fs,duration,f0,f1: float): int =
if (f0 >= fs/2) or (f1 >= fs/2):
stderr.writeLine("freq >= fs/2 !!")
return 1
var s = mkLogsweep1(fs, duration, f0, f1)
discard stdout.writeBuffer(s[0].addr, sizeof(s[0])*len(s))
dispatch logsweep1
特性は?
普通に計算したデータと最後の1秒を比較してみます。
正弦波
fs96kHz、120秒間、40001Hz のテスト信号(32bit wav)
青が普通に計算したもの、赤が今回のものです。
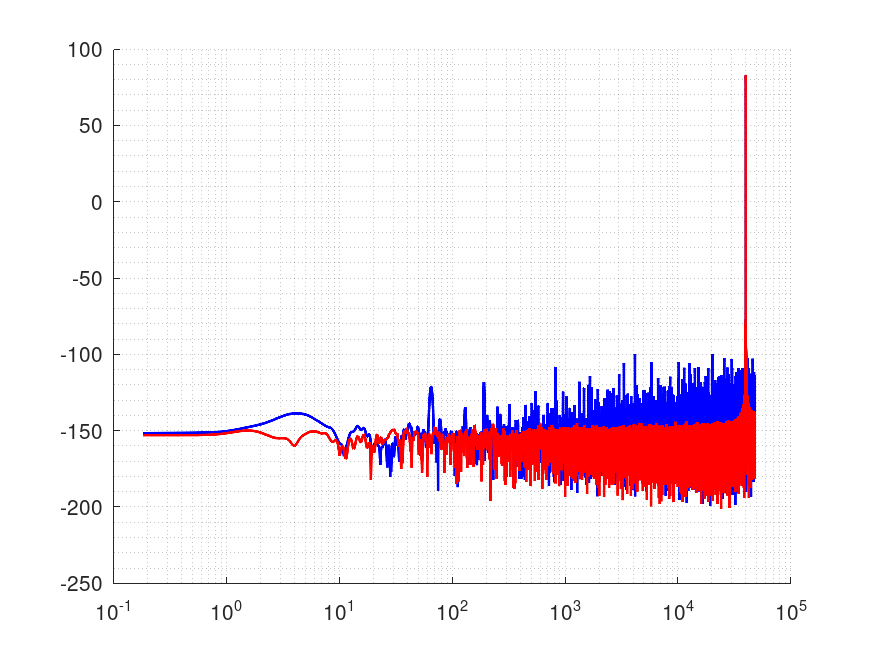
Fig.3
ご覧のように今回のプログラムのほうが精度が改善しています。
ログスイープ
fs96kHz、120秒間、20Hz-45000Hz のテスト信号(32bit wav)
やはり最後の1秒を比較します。
青が普通に計算したもの、赤が今回のものです。
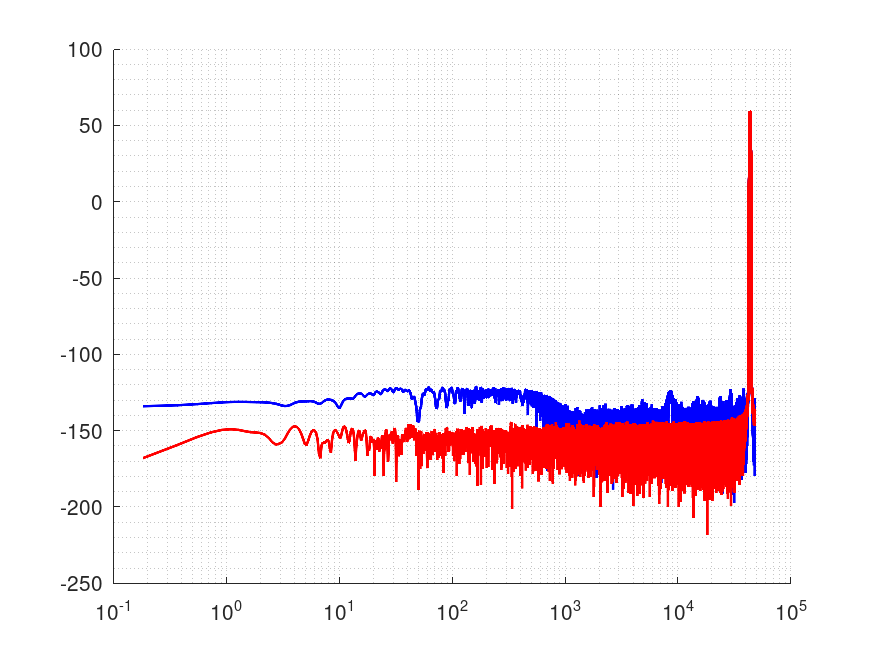
Fig.4
これも改善しています。
問題点
40001Hzの正弦波120秒の最初の1秒と最後の1秒の差を取るとゼロになりません。
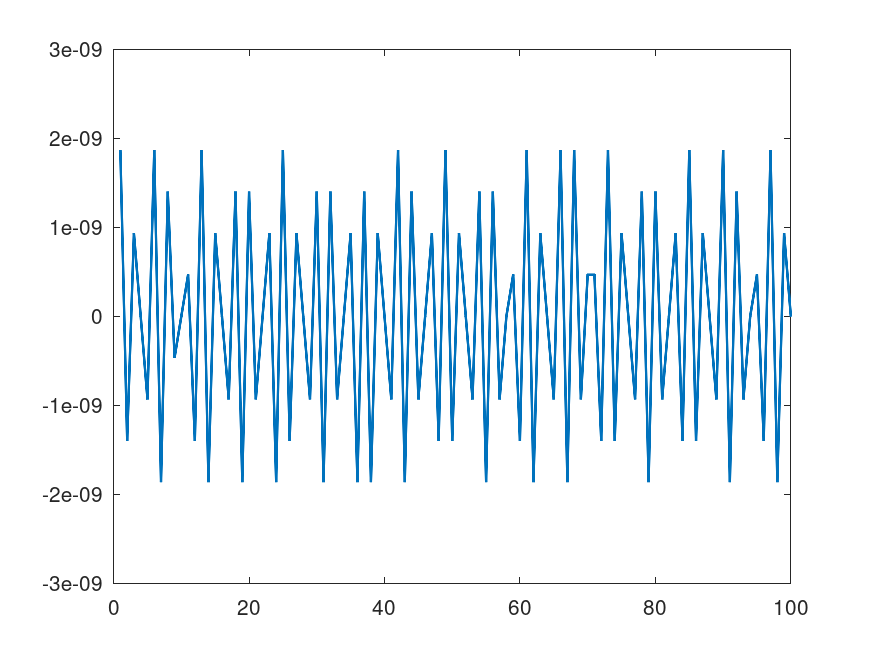
Fig.5
本来なら周波数が整数なので毎秒同じデータが繰り返されるはずです。
区間の面積を浮動小数点で求めているので誤差がでてしまうのです。
正弦波ならばその誤差がduration*fs倍されます。
そのためこの方法で計算した信号は周波数がわずかにずれる可能性があります。
誤差の最大値を見積もってみる
計算機イプシロン
計算機イプシロンとは
「1より大きい最小の数」と1との差 のこと。
倍精度浮動小数点では 2^(1-53) となります。
正弦波の誤差
正弦波の場合には周波数が一定なのでサンプル間の角度差も一定、同じ誤差がサンプル数だけ積算される。
サンプル間の角度差はπより小さいので誤差は計算機イプシロン*πより小さくなります。
従ってfs96kHz・120秒後の角度の誤差は
2^(1-53)*96000*120 * Pi
= 8.036049019411888e-09
より小さくなります。
普通に計算した時の120秒後の小数点以下の精度が8桁程度になっていたので、まあまあ十分な値かと思われます。
ログスイープの誤差
周波数が変化していくので誤差も変化していきます。
誤差も正負ばらけるのでトータルでは正弦波の場合よりも少なくなることが期待できます。
とりあえずこれで良いのか?
これで倍精度浮動小数点を使って32bit wavをほぼ正確に作れます。
しかし積分可能な関数なのにシンプソン公式で計算したほうが精度が良いというのもなんだかスッキリしない。
というわけで別の手段を考えます。
精度が足りなければ精度を上げればよいじゃないか!
浮動小数点には種類があって、倍精度浮動小数点よりも高精度なものもあります。
C言語で四倍精度浮動小数点数 (binary128) を使う
環境によって使えるものが違うのが欠点です。
GCCのlibquadmathで試していきます。armでは動きません。
Nim で四倍精度浮動小数点を使う
GCCで四倍精度浮動小数点(quadmath)が使えるなら Nim でも使えるはずです。
nimble search で探しても見つかりませんでした。
Google先生に聞いたらラッパーが見つかりました。
https://github.com/rforcen/nim/blob/add-license-1/quadmath.nim
ライセンスはMITなので修正していきます。
変更点
- 自然対数がlog なのを ln に置換 (nim の std/math に合わせた)
- 四倍精度浮動小数点を倍精度にキャストする関数 f64 を追加
- 文字列変換の桁数を増やした
検証用に修正したコードを置いておきます
ライセンス表記をどうすればよいのかよくわからなかったので調べた。
https://zenn.dev/noraworld/articles/license-copyright
修正したquadmath.nim
#MIT License
#
#Copyright (c) 2023 roberto forcen
#Copyright (c) 2023 Amanogawa Audio Labo
#
#Permission is hereby granted, free of charge, to any person obtaining a copy
#of this software and associated documentation files (the "Software"), to deal
#in the Software without restriction, including without limitation the rights
#to use, copy, modify, merge, publish, distribute, sublicense, and/or sell
#copies of the Software, and to permit persons to whom the Software is
#furnished to do so, subject to the following conditions:
#
# The above copyright notice and this permission notice shall be included in all
# copies or substantial portions of the Software.
#
# THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
# IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
# FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
# AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
# LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
# OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE
# SOFTWARE.
#Original Project https://github.com/rforcen/nim/blob/add-license-1/quadmath.nim
#Modified by AmanogawaAudioLabo
# quadmath.nim, __float128 wrapper
# doc: https://gcc.gnu.org/onlinedocs/libquadmath
{.passL: "-lm -lquadmath".}
type float128* {.importc: "__float128".} = object
const math_header = "<quadmath.h>"
# wrap
{.push inline.}
proc `+`*(x, y: float128): float128 = {.emit: [result, "=x+y;"].}
proc `-`*(x, y: float128): float128 = {.emit: [result, "=x-y;"].}
proc `-`*(x: float128): float128 = {.emit: [result, "=-x;"].}
proc `*`*(x, y: float128): float128 = {.emit: [result, "=x*y;"].}
proc `/`*(x, y: float128): float128 = {.emit: [result, "=x/y;"].}
proc `^`*(x, y: float128): float128 = {.emit: [result, "=pow(x,y);"].}
proc `+=`*(x: var float128, y: float128) = {.emit: "*x+=y;".}
proc `-=`*(x: var float128, y: float128) = {.emit: "*x-=y;".}
proc `*=`*(x: var float128, y: float128) = {.emit: "*x*=y;".}
proc `/=`*(x: var float128, y: float128) = {.emit: "*x/=y;".}
proc `==`*(x, y: float128): bool = {.emit: [result, "=x==y;"].}
proc `!=`*(x, y: float128): bool = {.emit: [result, "=x!=y;"].}
proc `>=`*(x, y: float128): bool = {.emit: [result, "=x>=y;"].}
proc `<=`*(x, y: float128): bool = {.emit: [result, "=x<=y;"].}
proc `>`*(x, y: float128): bool = {.emit: [result, "=x>y;"].}
proc `<`*(x, y: float128): bool = {.emit: [result, "=x<y;"].}
proc sin*(x: float128): float128 {.importc: "sinq", header: math_header.}
proc cos*(x: float128): float128 {.importc: "cosq", header: math_header.}
proc tan*(x: float128): float128 {.importc: "tanq", header: math_header.}
proc sinh*(x: float128): float128 {.importc: "sinhq", header: math_header.}
proc cosh*(x: float128): float128 {.importc: "coshq", header: math_header.}
proc tanh*(x: float128): float128 {.importc: "tanhq", header: math_header.}
proc asin*(x: float128): float128 {.importc: "asinq", header: math_header.}
proc acos*(x: float128): float128 {.importc: "acosq", header: math_header.}
proc atan*(x: float128): float128 {.importc: "atanq", header: math_header.}
proc atan2*(x, y: float128): float128 {.importc: "atan2q", header: math_header.}
proc pow*(x, y: float128): float128 {.importc: "powq", header: math_header.}
proc exp*(x: float128): float128 {.importc: "expq", header: math_header.}
proc ln*(x: float128): float128 {.importc: "logq", header: math_header.}
proc log10*(x: float128): float128 {.importc: "log10q", header: math_header.}
proc sqrt*(x: float128): float128 {.importc: "sqrtq", header: math_header.}
proc floor*(x: float128): float128 {.importc: "floorq", header: math_header.}
proc ceil*(x: float128): float128 {.importc: "ceilq", header: math_header.}
proc abs*(x: float128): float128 {.importc: "fabsq", header: math_header.}
# conversions
converter fto128*(f: float): float128 = # {.emit:[result, "=(__float128)f; "].} # this mangles vsc coloring
var r: float128; {.emit: "r=(__float128)f; ".}; r
converter ito128*(i: int): float128 = # {.emit:[result, "=(__float128) i;"].}
var r: float128; {.emit: "r=(__float128)i; ".}; r
converter f128toi*(f: float128): int =
var r: cint; {.emit: "r=(int)f; ".}; r.int
converter sto128*(s:cstring): float128 = {.emit:[result, "=strtoflt128 (s, NULL);"].}
converter sto128*(s:string): float128 = s.cstring.sto128
proc f64*(f: float128): float64 = #added by AmanogawaAudioLabo
var r: cdouble; {.emit: "r=(double)f; ".}; r.float64
let # constants
FLT128_MAX* = "1.18973149535723176508575932662800702e4932Q".float128
FLT128_MIN* = "3.36210314311209350626267781732175260e-4932Q".float128
FLT128_EPSILON* = "1.92592994438723585305597794258492732e-34Q".float128
FLT128_DENORM_MIN* = "6.475175119438025110924438958227646552e-4966Q".float128
M_Eq* = "2.718281828459045235360287471352662498Q" # e
M_LOG2Eq* = "1.442695040888963407359924681001892137Q" # log_2 e
M_LOG10Eq* = "0.434294481903251827651128918916605082Q" # log_10 e
M_LN2q* = "0.693147180559945309417232121458176568Q" # log_e 2
M_LN10q* = "2.302585092994045684017991454684364208Q" # log_e 10
M_PIq* = "3.141592653589793238462643383279502884Q" # pi
M_PI_2q* = "1.570796326794896619231321691639751442Q" # pi/2
M_PI_4q* = "0.785398163397448309615660845819875721Q" # pi/4
M_1_PIq* = "0.318309886183790671537767526745028724Q" # 1/pi
M_2_PIq* = "0.636619772367581343075535053490057448Q" # 2/pi
M_2_SQRTPIq* = "1.128379167095512573896158903121545172Q" # 2/sqrt(pi)
M_SQRT2q* = "1.414213562373095048801688724209698079Q" # sqrt(2)
M_SQRT1_2q* = "0.707106781186547524400844362104849039Q" # 1/sqrt(2)
proc sign*(x: float128): int =
if x<0: -1
elif x>0: 1
else: 0
proc lmod*(x: float128): (float128, int) =
var
i: float128
fract: float128
{.emit: "fract=modfq(x, &i);".}
(fract, i.int)
{.pop.}
# complex numers a+ib
import math
type Complex128* = object
re, im : float128
{.push inline.}
proc complex128*:Complex128=Complex128(re:0.0, im:0.0)
proc complex128*(re, im:float128):Complex128=Complex128(re:re, im:re)
proc arg*(z: Complex128): float128 = atan2(z.im, z.re)
proc sqmag*(z: Complex128): float128 = z.re*z.re + z.im*z.im
proc abs*(z: Complex128): float128 = z.sqmag.sqrt
proc `+`*(x, y: Complex128): Complex128 = Complex128(re: x.re + y.re, im: x.im + y.im)
proc `-`*(x, y: Complex128): Complex128 = Complex128(re: x.re - y.re, im: x.im - y.im)
proc `-`*(x: Complex128): Complex128 = Complex128(re: -x.re, im: -x.im)
proc `*`*(x, y: Complex128): Complex128 = Complex128(re: x.re*y.re - x.im*y.im, im: x.re*y.im + x.im*y.re)
proc `/`*(x, y: Complex128): Complex128 =
let d = (y.re*y.re) + (y.im*y.im)
result.re = (x.re*y.re)+(x.im*y.im)
result.re/=d
result.im = (x.im*y.re)-(x.re*y.im)
result.im/=d
proc `+`*(x: Complex128, y: float): Complex128 = Complex128(re: x.re + y, im: x.im + y)
proc `-`*(x: Complex128, y: float): Complex128 = Complex128(re: x.re - y, im: x.im - y)
proc `*`*(x: Complex128, y: float): Complex128 = Complex128(re: x.re * y, im: x.im * y)
proc `/`*(x: Complex128, y: float): Complex128 = Complex128(re: x.re / y, im: x.im / y)
proc `+=`*(x: var Complex128, y: Complex128) = x = x+y
proc `-=`*(x: var Complex128, y: Complex128) = x = x-y
proc `*=`*(x: var Complex128, y: Complex128) = x = x*y
proc `/=`*(x: var Complex128, y: Complex128) = x = x/y
proc `+=`*(x: var Complex128, y: float) = x.re+=y; x.im+=y
proc `-=`*(x: var Complex128, y: float) = x.re-=y; x.im-=y
proc `*=`*(x: var Complex128, y: float) = x.re*=y; x.im*=y
proc `/=`*(x: var Complex128, y: float) = x.re/=y; x.im/=y
proc sqr*(z: Complex128): Complex128 = z*z
proc pow3*(z: Complex128): Complex128 = z*z*z
proc pow4*(z: Complex128): Complex128 = z*z*z*z
proc pow5*(z: Complex128): Complex128 = z*z*z*z*z
proc pown*(z: Complex128, n: int): Complex128 =
result = z
for i in 1..n: result*=z
proc pow*(z: Complex128, n: int): Complex128 =
let
rn = z.abs().pow(n)
na = z.arg() * n.ito128
Complex128(re: rn * cos(na), im: rn * sin(na))
proc pow*(s, z: Complex128): Complex128 = # s^z
let
c = z.re
d = z.im
m = pow(s.sqmag, c/2.0) * exp(-d * s.arg)
result = Complex128(re: m * cos(c * s.arg + 0.5 * d * ln(s.sqmag)), im: m * sin(
c * s.arg + 0.5 * d * ln(s.sqmag)))
proc sqrt*(z: Complex128): Complex128 =
let a = z.abs()
Complex128(re: sqrt((a+z.re)/2.0), im: sqrt((a-z.re)/2.0) * sign(z.im).ito128)
proc ln*(z: Complex128): Complex128 = Complex128(re: z.abs.ln, im: z.arg)
proc exp*(z: Complex128): Complex128 = Complex128(re: E, im: 0.0).pow(z)
proc cosh*(z: Complex128): Complex128 = Complex128(re: cosh(z.re) * cos(z.im), im: sinh(z.re) * sin(z.im))
proc sinh*(z: Complex128): Complex128 = Complex128(re: sinh(z.re) * cos(z.im), im: cosh(z.re) * sin(z.im))
proc sin*(z: Complex128): Complex128 = Complex128(re: sin(z.re) * cosh(z.im), im: cos(z.re) *
sinh(z.im))
proc cos*(z: Complex128): Complex128 = Complex128(re: cos(z.re) * cosh(z.im), im: -sin(z.re) *
sinh(z.im))
proc tan*(z: Complex128): Complex128 = z.sin()/z.cos()
proc asinh*(z: Complex128): Complex128 =
let t = Complex128(re: (z.re-z.im) * (z.re+z.im)+1.0, im: 2.0*z.re*z.im).sqrt
(t + z).ln
proc asin*(z: Complex128): Complex128 =
let t = Complex128(re: -z.im, im: z.re).asinh
Complex128(re: t.im, im: -t.re)
proc acos*(z: Complex128): Complex128 =
let
t = z.asin()
pi_2 = 1.7514
Complex128(re: pi_2 - t.re, im: -t.im)
proc atan*(z: Complex128): Complex128 =
Complex128(
re: 0.50 * atan2(2.0*z.re, 1.0 - z.re*z.re - z.im*z.im),
im: 0.25 * ln((z.re*z.re + (z.im+1.0)*(z.im+1.0)) / (z.re*z.re + (z.im-1.0)*(z.im-1.0)))
)
{.pop.}
# end Complex128 - Complex128
{.emit:"#include <stdio.h>".}
proc `$`*(x: float128): string =
var
conv_buff: array[256, char]
cl: cint
{.emit: " cl=quadmath_snprintf (conv_buff, 255, \"%.40Qg\", x); ".}
for i in 0..<cl: result.add(conv_buff[i])
# factorial
proc `!`*(n: int): float128 =
if n > 0: n.float128 * !(n-1) else: 1.0
# test
when isMainModule:
proc test_f128=
var f0, f1, f2: float128
f1 = 123.45
f2 = 456.78
echo "max:", FLT128_MAX, ", min:", FLT128_MIN, ", 123.456=", "123.456Q".float128
echo "fin.sin=", f1.sin
echo f1, ",", f2, ",",f1+f2
# assert comps
assert f1 != f2
assert f1 == f1
assert f2 >= f0
assert f2 > f1
assert f1 < f2
assert f1 <= f2
# assert algebra
assert f1+f2 == 123.45.float128 + 456.78.float128, "+ doesn't work"
assert f1-f2 == 123.45.float128 - 456.78.float128, "- doesn't work"
assert f1*f2 == 123.45.float128 * 456.78.float128, "* doesn't work"
assert f1/f2 == 123.45.float128 / 456.78.float128, "/ doesn't work"
assert f1+f2 != (123.45 + 456.78).float128
f1+=f2
echo "+=", f1, "==", 123.45+456.78
f0 = f1+f2*f1
echo "f0=f1+f2*f1=", f0, ", f1=", f1, ", f2=", f2
echo "factorial(900) * 4 = ", !900 * 4
f1 = f1^(f2/10)
echo "f1.some func = ", f1.sin.sinh.atan.floor.exp.ln
f2 = 123.456.float128.sqrt
f0 = -678.89.float128
echo f0, ", ", f0.abs
echo 123.456.sqrt, ", ", f2.abs
echo f2, ", ", f2.lmod
echo "atan2=", atan2(f1,f2)
# seq's
var sf: seq[float128]
for i in 0..100:
var f: float128
case i %% 3:
of 0: f = f0
of 1: f = f1
of 2: f = f2
else: f = f0
sf.add(f)
echo sf[0..10], sf[sf.high-10..sf.high]
import times, complex, sugar
proc test_c128=
var
c0 = complex128(1, 0)
z = c0
zv = newSeq[Complex128](100)
# init all items in vect, notice that z=c0 will not work
for z in zv.mitems: z = c0
let zzv = collect(newSeq):
for i in 0..100:
z
for zz in zzv: z+=zz
echo "z=", z
z = c0
c0+=123.67
let n = 4000
echo "generating Complex128 ", n*n
var t0 = now()
for i in 0..n*n: # simulate mandelbrot fractal generation
z = c0
for it in 0..200:
z = z*z+c0
if z.abs > 4.0: break
echo z
echo "lap Complex128:", (now()-t0).inMilliseconds, "ms"
var
dz = complex64(1, 0)
dc0 = dz
dc0 += complex64(123.67, 123.67)
t0 = now()
for i in 0..n*n:
dz = dc0
for it in 0..200:
dz = dz*dz+dc0
if dz.abs > 4.0: break
echo dz
echo "lap complex 64:", (now()-t0).inMilliseconds, "ms"
test_f128()
# test_c128()
使い方
import quadmath # std/math をimport しなくても float128 の数学関数は使える
import std/math # float64 で数学関数を使うなら std/math が必要
# converter sto128 が定義してあるので文字列がfloat128に変換される
echo "1.0e-10" / 3.0
#float(64bit)と解釈されてからfloat128に変換されるので精度が出ない
echo float128(1.11111111111111111111111111111111111111)
#文字列で与えればよい
echo float128("1.11111111111111111111111111111111111111")
var a1: array[4,float128] #配列
var a2 = newSeq[float128](4) #動的配列
#echo sqrt(2'f128) #Error この記法は使えない
echo sqrt((2).float128) # intをfloat128 に変換
echo sqrt((2.0).float128) # floatをfloat128 に変換
var
x: int = 2
y1: float128 = x.float64 #暗黙の型変換
#y2: float64 = x.float128 #Error
y3 = sqrt(x.float128).f64 #float64 に変換するのには f64
echo y1, " ", y3
# どちらも誤差があって0にならないが、float128のほうが精度が格段に良い
echo sin(Pi*10000000.0) # Pi はfloat64
echo sin(M_PIq*1000000.0) # M_PIq はfloat128
echo ln(float128(2)) # 自然対数はlogではなくlnに変更した
四倍精度で計算する
早速四倍精度で計算してみます。
最初のプログラムとほとんど同じです。
正弦波(四倍精度版)
tone2.nim
import quadmath
proc mkTone2*(fs, duration, f: float): seq[float64] =
var s = newSeq[float64]((fs*duration).int)
for n in 1..<(fs*duration).int:
s[n] = sin(n.float128/fs * f * float128(2) * M_PIq).f64
return s
#=================
when isMainModule:
import cligen
proc tone2(fs, duration, f: float): int =
if f >= fs/2:
stderr.writeLine("ERROR! f >= fs/2")
return 1
var s = mkTone2(fs, duration, f)
discard stdout.writeBuffer(s[0].addr, sizeof(s[0])*len(s))
dispatch tone2
ログスイープ(四倍精度版)
logsweep2.nim
import quadmath
proc mkLogsweep2*(fs: float128, duration: float128, f0: float128, f1: float128): seq[float64] =
proc integr(t: float128): float128 =
pow(f1/f0, t/duration) / ln(f1/f0) * f0 * duration
var s = newSeq[float64]((fs*duration).int)
let angle0 = integr(0)
for n in 1..<(fs*duration).int:
var angle1 = integr(n.float128/fs)
s[n] = sin((angle1 - angle0)*2.0*M_PIq).f64
return s
#============================================================
when isMainModule:
import cligen
proc logsweep2(fs,duration,f0,f1: float): int =
if (f0 >= fs/2) or (f1 >= fs/2):
stderr.writeLine("freq >= fs/2 !!")
return 1
var s = mkLogsweep2(fs, duration, f0, f1)
discard stdout.writeBuffer(s[0].addr, sizeof(s[0])*len(s))
dispatch logsweep2
速度
かなり遅いですが実用範囲内です。
倍精度浮動小数点の50-70倍位の時間がかかります。
精度
fs96kHz、120秒間、40001Hz、32bit wav の最初の1秒と最後の1秒の差を見ると完全に一致します。
結論
- 32bit wav のテスト信号を作るのに倍精度浮動小数点では精度が足りない
- Octave の symbolic package は速度が遅いのでテスト信号作成には辛い
- 倍精度浮動小数点の場合、積分するよりもシンプソン公式で計算したほうが精度がでる
- 四倍精度浮動小数点は 32bit wav のテスト信号を作るのに十分な精度がある
おまけ
私のオーディオのメインシステムはHDMIからLPCM8chで出力するマルチアンプシステムになってます。
HDMIからのLPCM8ch出力は24bitまでしか出力できません。
したがって32bitデータを送ろうとしても下位8bitは切り捨てられてしまいます。
テスト信号をがんばって32bit精度で作っても全く意味がありませんでした。
チャンチャン。