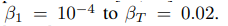LoginSignup
56
44

More than 1 year has passed since last update.

@asparagasu(アスパラ)

Diffusion Model

Last updated at Posted at 2022-04-02

何についての記事か

  • Diffusion Modelについて
    • VAEなどの画像生成関連知識と対比して

論文

Denoising Diffusion Probabilistic Models
(NeurIPS 2020)

何がすごいか

  • 拡散過程で画像を生成するという新しい概念
  • VAEと異なりエンコード側の学習パラメータが存在しない
  • 性能というよりも、画像生成手法の進化方向が分かる、つかめる点が面白い
    • オートエンコーダ→VAE→Flow→Diffusion Model
  • 高解像度化→テキストから画像への変換などの進化を遂げ始めている
    • GLIDE　Diffusion Model +　CLIPの構成
      image.png

画像生成のこれまで

Diffusion ModelがVAEにいているので主にVAEについて。
VAEについての記事はこちら①こちら②が分かりやすかった。

VAEの構成としては以下のようになっており、画像（事前分布$x_{1}$~$x_{N}$）を入力して、それを潜在変数zにエンコードして、デコードで画像（事後分布$ \hat{x}1$ ~$\hat{x}N$）を再構築する流れになっている。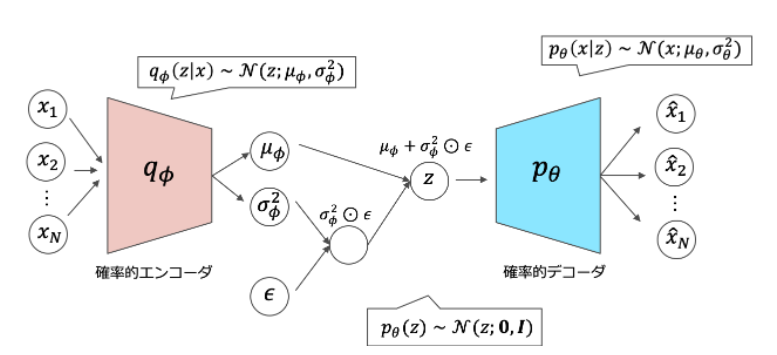image.png

潜在変数zをガウス分布と仮定し、エンコードでは平均と分散を出力するようにNNを学習する。
エンコード側、デコード側もガウス分布と仮定することでNNの損失関数を解析的に求めることが可能となった。

$p_{Θ}(x|z)$の尤度を最大化するように学習したい。（＝潜在変数zの時に生成される画像Xが入力と確からしいように学習したい）
その時に登場するのが変分下限であり、目的関数を近似すうことができる。最終的に求められる目的関数が以下となる。
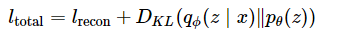
image.png
再構築誤差（入力分布と出力分布の確からしさの判断）+ 潜在空間の分布の良さ（どれだけガウス分布に近いか）から表される。
潜在空間の分布は正ガウス分布を期待するので$q_{Θ}(z|x)$と正規分布の分布間の距離KLダイバージェンスをとっている。
再構築誤差も小さく、潜在空間の分布も期待通りであればLは小さくなる。

ここでエンコードとデコードがガウス分布の場合KLダイバージェンスは一般的に以下のように解析的に計算できる。このように解析的に計算したいため、エンコードとデコードをガウス分布と仮定している。
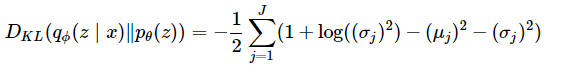
image.png

Diffusion Modelのアイデア

image.png

  • ガウスノイズを画像に対して順次かけていき（Forward）、完全にガウス分布後に、ノイズを予測して画像を生成する（Reverse）
    • kolmgorov equationの適用
      • 「順方向（Diffuse：ガウシアンの付加）の変化量が十分に小さい場合、逆変換も同様の関数系（ガウシアン）で表せる」という性質
      • ForwardもReverseもガウス分布とすることで、ガウス分布の性質（KLダイバージェンスが解析的に計算可能、平均と分散だけを推論すればよい）が使える
    • Fowardはガウスノイズを固定でかけるだけにすることで、Foward側には学習パラメータをなくす
    • 画像生成時(reverse)の時は画像にかけられているノイズを推測して取り除いていく
    • Fowardでかけるノイズの分散は時刻tにより決まっているので、本モデルでは平均だけを推論できればよい

これらのアイデアでより高精度で多様な画像生成を実現しようとした。

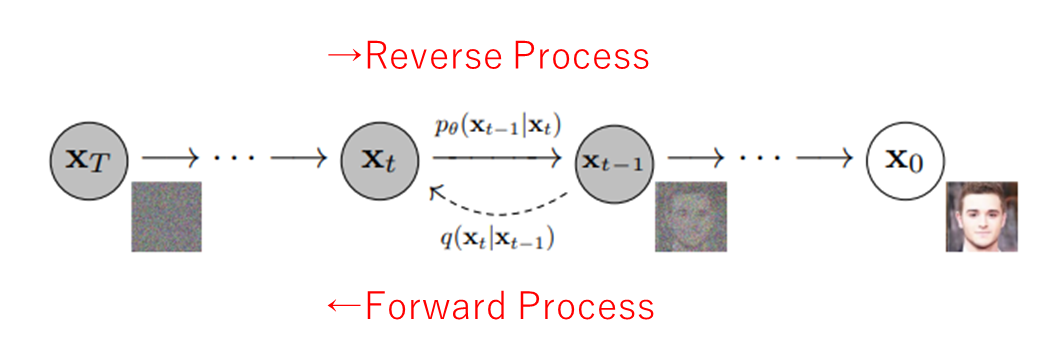
Diffusion Process

image.png

  • Forward Process: 複雑な分布 (X0)に少しずつガウシアンノイズを加えてガウス分布(XT)に変換する過程(左方向。学習なし)
  • Reverse Process: ガウス分布(XT)からガウシアンノイズをを取り除いていき複雑な分布 (X0)を作る過程（右方向。学習あり）

Forward Process

複雑な分布 q(X0)に少しずつガウシアンノイズを加えてガウス分布(XT)に変換する過程は以下のように表される。
前回の画像Xt-1からXt(t=1~T)への変換を掛け合わせることで最終的にXTに変換される。
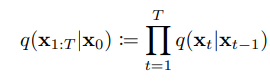
image.png

Xt-1からXtに変換する為に加えるノイズは平均$\sqrt{1-β_t}x_{t-1}$ 分散$β_tI$のガウシアンノイズであり以下のように表される。
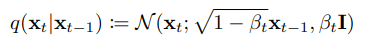
image.png

この変換を加えることで最終的には完全なガウシアンノイズになる。(T→∞)
論文中ではT＝1000。またステップが重なるごとにノイズは大きくかける$β1 < β2 < ・・・<βt $（Langevin動力学と似ているらしい）

Reverse Process

ガウス分布(XT)からガウシアンノイズをを取り除いていきX0を作る過程は以下のように表される。
P($x_T$)に対してForward Processとは逆で$x_t$から$x_{t-1}$に変換する処理を順次かけていく。
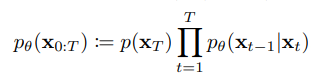
image.png

変換に使用する処理は以下の平均と分散を持つガウシアンノイズをかけることである。Θは学習したいパラメータ。
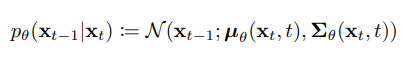
image.png

xtの分布から、あるサンプルをサンプリングして得られた画像の平均に対して、σzを付加して$x_{t-1}$の分布を作り出している。
$x_{t-1}$=$μ_{Θ}(xt,t)$+$σ_{t}z$
σはFowardの時の値を使用している。

微小時刻$t-1$から$t$の変化が十分に小さい場合は、その逆変換$t$から$t-1$の変換もガウス分布で表すことができることを利用している。

学習

時刻tで付加されているノイズを見破れるように学習していく。

VAE同様に変分下限で$p(Θ)$の対数尤度を最大化することを目指す
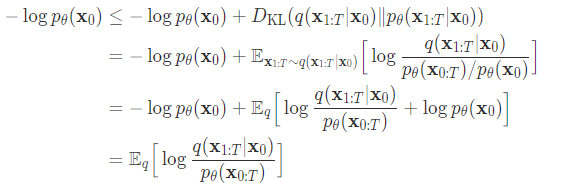
image.png

Eの中を計算できればよいので以下のように展開する
image.png

$LT$はノイズをかけた最終分布同士の比較なので定数、$L0$は計算可能。$Lt$は時刻tの時のFowardとReverseの分布間距離。
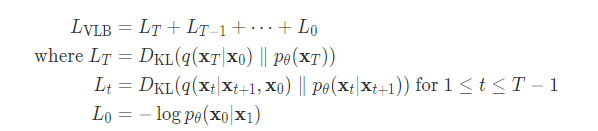
image.png

従って、変分下限を最大化することはLtを最小化すればよいことと同値になる。
また、本モデルでは分散は時刻tで決まっているので、時刻tにおける平均の予測誤差を最小化すればよいとなる。

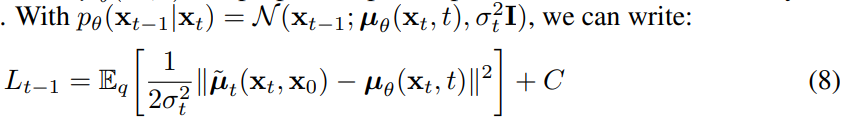
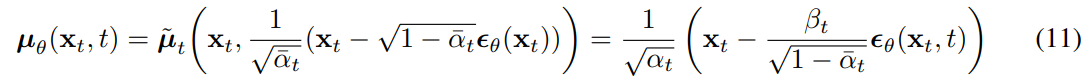
image.png
image.png
平均は式11のように表されるので(8)に(11)を代入すると以下のようになり、
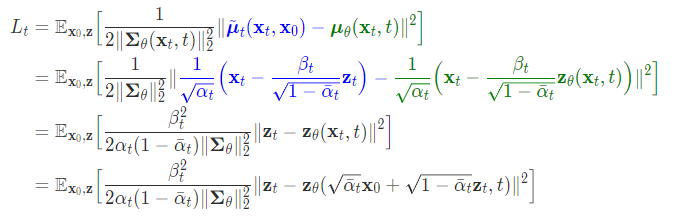
image.png
$t$と$x_{t}$はForwardプロセスで使用しているので利用可能なのでそこからzを計算可能となる。

最終的にシンプルにした式が以下。前に付いている係数がない方が性能が良かったのでなくしたらしい。
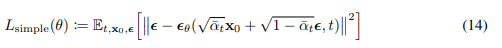
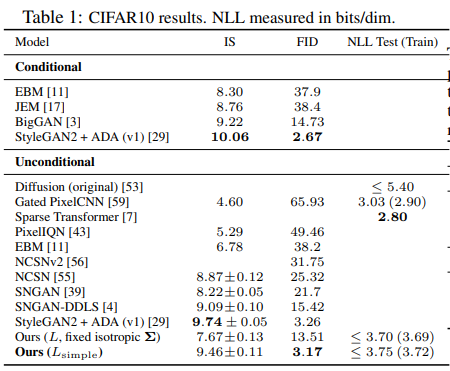
image.png

参考にしたBLOG

実験結果

  • すべての実験はT＝1000

  • βは以下の値で線形に変化するように設計
    image.png

  • U-Netを使用

  • 生成画像の品質結果
    以下のような画像を生成
    image.png

    • Inseptionスコアが高く、FIDが高いので非常に良いという結果。多様な画像を高品質で生成できていることを意味する。

image.png

  • 画像生成の実験

    • 画像生成の過程
      image.png
    • 同じ潜在変数から生成された画像からどのような画像が生成されるか
      • tが小さい画像から生成された画像は大きな特徴しか同じでない
      • tが大きい画像(t=250など)は詳細もほぼ同じ
      • 上記の特徴が概念的圧縮"Conceptual Compression"のヒントになるかもと言っているが良く分からなかった。
        • より高いレベル（画像を象徴する特徴）から圧縮されていることを概念的圧縮という
        • tが小さいほどかけるノイズが小さかったから詳細が復元されるのは普通な気もするが...
          image.png

  • 画像の補完

    • 混ぜるSourceは左右の端の画像、Sourceをそれぞれ再構築（ノイズに変換→再構築）して生成した画像がRec.
    • λの値で線形補完して生成した画像をそれぞれ再構築した画像がλに対応する画像
    • こんな感じでいろんな画像が作れる。いい感じで補完してノイズを消してくれているしてくれている。
      image.png
56
44
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
56
44