この記事は「データ構造とアルゴリズム Advent Calendar 2020」16日目の記事です。
15日目の記事はyurahunaさんの「木分解上の動的計画法」で、
17日目の記事はtsukasa__diaryさんの「Lawler の K-Best 列挙アルゴリズム」です。
この記事内で使用しているプログラムやそのテストプログラムは全て以下のGitHubリポジトリで閲覧可能です。プログラムの詳細に興味がある方はこちらをご覧ください(ついでにStarを押していってくれると喜びます🙂)。
Github: ashiba/Imprementation_of_IKERUKANA: Momotaro Dentetsu is a game.
変更履歴
2020/12/21に「最終的に貧乏神が付かない移動方法 ~貧乏神持ちの場合~」, 「最終的に貧乏神が付かない移動方法 ~貧乏神がついていない場合~」, 「PS2での実行時間に関する考慮について」を追記しました。
記事内容要約
- Switch版桃太郎電鉄における「いけるかな」機能を実現するアルゴリズムを考察・実装した。
- 桃太郎電鉄シリーズにおいて実装されていない「貧乏神が付くか否かを確実に予測」するアルゴリズムについて考察・実装した。
- 貧乏神を考慮した「いけるかな」が実装されていない理由を、過去の桃太郎電鉄シリーズが発売されているゲーム機のプロセッサ性能の面も考慮し、考察した。
記事執筆のきっかけ(桃鉄知ってる人向け)
桃太郎電鉄で遊んでいて、「いけるかな」機能を使うと以下のようなメッセージが出る場合があります。これは「いけるかな」機能において、計算時間の関係で「貧乏神が付くか否かを確実に予測」する機能は持たず、簡易的な判別を行っていることを示しています。しかし、これを実現する計算はそんなに複雑でしょうか?「1時間ぐらいかかるそうです!」とのことですが、僕は「これは動的計画法的なアプローチでまともな実行時間で解けるんじゃないか?🤔」と思い、アルゴリズムの考察を始めました。これが本記事執筆のきっかけです。
「この経路を 通ると ひょっとすると 貧乏神が くっつくかも しれません」
「<いけるかな>は 高性能ですが 大きな数字を出したときに 貧乏神が くっつくかどうかを 計算すると…」
「なんと! 1兆通りにもなって 計算だけで 1時間ぐらい かかるそうです!」
「そんなわけで ひょっとすると 貧乏神がつくかも? というときだけ 私が 助言させていただきます」
「私の 適当な 助言でも 1時間待つよりはいいですよね?」
桃鉄のルールと「いけるかな」機能の解説
桃鉄のルールや「いけるかな」機能の解説です。すでにご存じの方はここは読み飛ばしていただいて構いません。
桃鉄について
最近流行っていますね、桃太郎電鉄。桃鉄こと桃太郎電鉄は「日本全国各地がすごろくのマスになり、プレイヤーの誰かが到達するごとに変化する"目的地マス"をめざしてすごろくの盤面上を右往左往するゲームです。参考: 桃太郎電鉄シリーズ - Wikipedia
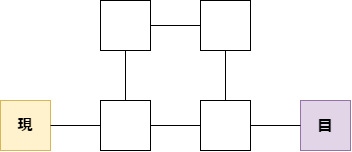
桃鉄では、プレイする中で"目的地マス"にピッタリ止まることが要求される場面が多々あります。一般的なすごろくでは、サイコロは1つであり出目が1~6程度であることが多いことや、ゴールまでの道のりが一本道であることが多いことから、現在の出目でゴールに到達することが可能かを判別することは比較的容易です。一方桃鉄の場合は必ずしもそうは行きません。なぜなら、サイコロの数は最大で8個まで増えるし、盤面には多くの閉路を含むためです。例えば以下の図のような例を考えてみましょう。ここで、「現」と書いてある黄色のマスを現在地マス、「目」と書いてある紫色のマスを目的地マスとします。
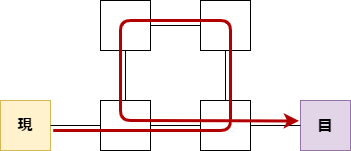
さて、ここでサイコロの出目が7であった場合に目的地マスにピッタリ止まることは可能でしょうか?その答えはYESです。最短経路で目的地マスに向かえば3ステップしか消費しませんが、以下の図のように閉路を反時計回りにぐるっと回ることで7ステップピッタリ消費して目的地マスにたどり着くことができます。
賢明な読者のみなさまならお気づきかと思いますが、このような状況では7以外にも11, 15, 19など、出目が4N+3(Nは正の整数)の形で表せる数であればゴールが可能ですし、閉路を逆向きの時計回りに回ることで4N+1(Nは正の整数)の形で表せる数であってもゴールが可能です。今回は目的地マスにピッタリ止まることができる出目を数式の形で列挙することができましたが、もっと閉路が増えるとそうは行きません。列挙のためには移動方法の探索を行うなどのアプローチが必要となります。この「そのときの出目で特定のマスにぴったり止まることができるか?」という問題は桃鉄では重要な問題でありながら、人間の手で解くには結構複雑な問題なのです。
貧乏神について
このゲームではプレイヤーのうち一人について回り、悪事を行う貧乏神という存在がいます。この貧乏神の悪事から逃れる方法の一つとして、他のプレイヤーになすりつけるという方法があります。貧乏神がついた状態で他のプレイヤーがいるマスを通過すると、すれ違ったプレイヤーに貧乏神をなすりつけることができます。一方自分に貧乏神がついていなくとも、貧乏神がついたプレイヤーがいるマスを通過した場合は自分に貧乏神が付いてきてしまいます。そのため桃鉄では、「このマスへ移動したいが、移動の過程で自分に貧乏神が付いてしまうことは避けたい」というような状況が時々発生します
「いけるかな」機能
そこで桃鉄に導入された機能が「いけるかな」機能です。この機能はサイコロを振った後に使用することができ、使用すると現在のマスからそのときの出目でピッタリ止まることができるマスを列挙し、到達可能なマスが光ってプレイヤーに教えてくれます。また、移動によって貧乏神がつく可能性があるかどうかを教えてくれます(貧乏神のなすりつけは確率的に起こるものではありませんが、なぜか断言はしてくれません。冒頭の"記事執筆のきっかけ"の部分の画像参照)。これを使えば現在のマスからそのときの出目で目的地マスにピッタリ止まることができるか?ということや、勝負に有利なアイテムがもらえるマスに止まることができるか?ということが一目でわかり、ゲームをプレイするにあたって非常に便利な機能です。本記事ではこの機能を実現するアルゴリズムについて考察・実装を行っていきます。
「いけるかな」機能を実現するアルゴリズムの考察と実装
愚直な幅優先探索
手始めに、貧乏神のなすりつけを考慮しない「いけるかな」のアルゴリズムを考えてみましょう。
「いけるかな」機能を言い換えると、「連結なグラフ上で、スタート地点となるノードからエッジを介して隣接しているノードへ移動する(ただし前回いたノードに戻ることはできない)ことをK回繰り返したときに、到達可能なノードを列挙せよ」という問題になります。これは深さKの幅優先探索で解くことができます。以下にそのプログラムを添付します。GitHub上の対応するコードは こちらです。
ここでソースコード中の関数の入力(引数)の一つである Graphは、Graph[i]がノードiに隣接するノードの集合を表す隣接グラフです。幅優先探索の処理では、remaining_move, node_num, directionの3つをメンバ変数として持つBFS_Statusを探索時の状態としています。各メンバ変数の説明は以下です。
| メンバ変数名 | 説明 |
|---|---|
| remaining_move | 残り移動可能ステップ数 |
| node_num | 現在いるノードのid |
| direction | 直前に通ったノードを記憶するために、そのノードに接続する頂点のうちidが何番目に小さいかを持つ |
なお、ここでdirectionの値を計算するために、getDirectionTableという関数を使用しています。配列サイズを大きくしたり、hashを利用したりしても良いのですが、配列サイズと状態数を一致させたいことや、hash(C++でいうとunordered_map)を使用してプログラムが実行する命令が読みづらくなることを懸念して、ここでは最低限のサイズを持った配列を使用しています。getDirectionTable関数の実装についてはGitHub上のこちらにあります。
探索時には現在いるノードに隣接している全てのノードへの移動をシミュレーションします。
桃鉄のマスの最大次数は4であるため隣接ノードへの移動は最大4通りです。このアルゴリズムの計算量を考えると、サイコロの出目(=移動数)をDとしたときに、このアルゴリズムはO(4^D)のアルゴリズムと言えます。Dが12程度ならば1秒以内に計算可能であることが予想できますが、桃鉄におけるサイコロの出目の最大値が48であることを考慮すると、ゲーム内のお助け機能としては実行時間がかなり厳しく、出目によっては処理が重すぎてしばらくゲームが固まってしまう可能性があります。
const std::set<size_t> solveBruteForce(const std::vector<std::vector<int>>& Graph, const int& PLAYER_POS, const int& DICE_NUM, const int& MAP_NUM) {
if (DICE_NUM == 0) {
return {0};
} else if (DICE_NUM < 0) {
std::cout << "DICE_NUM is less than 0 ??? ( " << DICE_NUM << " )" << std::endl;
return {};
}
std::set<size_t> reachable_nodes;
const std::vector<std::vector<char>> direction_table = getDirectionTable(Graph);
std::queue<BFS_Status> que;
que.push(BFS_Status{DICE_NUM, PLAYER_POS, NON_DIRECTION});
while(not que.empty()) {
const BFS_Status que_front = que.front();
que.pop();
assert(Graph[que_front.node_num].size() <= 4);
if ((int)que_front.remaining_move <= 0 ) { // 探索終了
assert((int)que_front.remaining_move == 0);
reachable_nodes.insert(que_front.node_num);
} else {
for (const int& dist_node: Graph[que_front.node_num]) { // 隣接するノードを探索
if (direction_table[que_front.node_num][dist_node] == que_front.direction) continue; // 前回通ったノードへの移動はNG
que.push(BFS_Status{que_front.remaining_move-1, dist_node, direction_table[dist_node][que_front.node_num]});
}
}
}
return reachable_nodes;
}
幅優先探索をメモ化
前述の幅優先探索では計算量がO(4^D)となり、サイコロの出目が大きい場合に実行時間が非常に長くなってしまうことがわかりました。そこで、この幅優先探索をメモ化することで無駄を省いて計算することにしましょう。この幅優先探索アルゴリズムでは、BFS_Statusのメンバ変数の値が全く同じデータが複数回queueに追加されることがあります。例えば以下のようなグラフを考えた場合、赤矢印の移動の結果も青矢印の移動の結果も、{移動回数、滞在しているノード、前回通ったノード}に着目すると全く同じです。このように、全く同じデータがqueueに追加された場合、それぞれのデータに対して幅優先探索が続けられるため、非常に無駄の多い探索となってしまいます。
そこで、BFS_Statusの値をキーとした配列を用意し、queueに追加しようとしている値がすでに探索済みである場合はqueueにpushしないことにします。これによって計算効率を大幅に改善することができます。これが一般的にメモ化と呼ばれる手法です。具体的な実装としては、dp[dice_sum][map_squares_num][direction]を状態とし、その状態がすでに探索済みであればtrue、そうでなければfalseを持つことにしています。以下にそのプログラムを添付します。GitHub上の対応するコードは こちらです。
さて、このアルゴリズムの計算量を考えてみましょう。幅優先探索によって探索される状態は、高々dp配列の要素数分となります。ここでも桃鉄のマスの最大次数は4であるという性質を使うと、サイコロの出目をD,桃鉄の盤面のサイズをMとしたときにO(DM)のアルゴリズムとなります。また、D回の移動で到達できないマスについては探索が行われないため、D回以内で移動できないマス目を考慮から外すことができます。桃鉄の盤面の最大次数は4となっており、ごく一部の例外(飛行機や船での移動)を無視すれば、平面グラフと言えます。このことから、最も密な盤面でも2次元のグリッドグラフ程度の辺の密度と言ってもおよそ問題ありません。グリッドグラフにおいてD回の移動で到達できるマスの数は(2D+1)^2/2+1(これは現在地からマンハッタン距離がDの範囲に含まれるマスの数です)であるため、盤面サイズMの上限はD^2のオーダーで押さえられることになります。
つまり、盤面が(2D+1)^2/2+1より十分に大きい場合にO(D^3)で、そうでない場合にO(DM)といえます。O(min(D^3, DM))とも書けますね。
const std::set<size_t> solveIkerukanaDP(const std::vector<std::vector<int>>& Graph, const int& PLAYER_POS, const int& DICE_NUM, const int& MAP_NUM) {
if (DICE_NUM == 0) {
return {0};
} else if (DICE_NUM < 0) {
std::cout << "DICE_NUM is less than 0 ??? ( " << DICE_NUM << " )" << std::endl;
return {};
}
std::set<size_t> reachable_nodes;
const std::vector<std::vector<char>> direction_table = getDirectionTable(Graph);
bool dp[DICE_NUM+1][MAP_NUM][DIRECTION_NUM];
memset(dp, 0, sizeof(dp));
std::queue<BFS_Status> que;
que.push(BFS_Status{DICE_NUM, PLAYER_POS, NON_DIRECTION});
while(not que.empty()) {
const BFS_Status que_front = que.front();
que.pop();
assert(Graph[que_front.node_num].size() <= 4);
if ((int)que_front.remaining_move <= 0) { // 探索終了
assert((int)que_front.remaining_move == 0);
reachable_nodes.insert(que_front.node_num);
} else {
for (const size_t& dist_node: Graph[que_front.node_num]) { // 隣接するノードを探索
if ((size_t)direction_table[que_front.node_num][dist_node] == que_front.direction) continue; // 前回通ったノードへの移動はNG
bool& dp_target_elm = dp[que_front.remaining_move-1][dist_node][(size_t)direction_table[dist_node][que_front.node_num]];
if (not dp_target_elm) {
que.push(BFS_Status{que_front.remaining_move-1, dist_node, (size_t)direction_table[dist_node][que_front.node_num]});
dp_target_elm = true;
}
}
}
}
return reachable_nodes;
}
貧乏神を考慮した「いけるかな」機能を実現するアルゴリズムの考察と実装
実はここまでの、貧乏神を考慮しない「いけるかな」の考察については、すでに同様の内容をまとめた記事がありました。ここからは、桃太郎電鉄のゲームにも実装されていない、貧乏神のなすりつけを考慮した「いけるかな」機能について考察・実装していきます。貧乏神のなすりつけにおいて、最終的に自分に貧乏神が付かないという条件を達成する移動にもいくつか種類があります。
最終的に貧乏神が付かない移動方法 ~貧乏神持ちの場合~ (2020/12/21 追記)
自分に貧乏神が付いている場合に、移動後に貧乏神が付いていない状態となるためには、移動中に他のプレイヤーになすりつける必要があります。移動中に他のプレイヤーに一度でも接触すれば貧乏神をなすりつけることができますが、一度貧乏神をなすりつけた他のプレイヤーに再度接触してしまうと、また自分に貧乏神がついてしまいます。そのため、「他のプレイヤーのいるマスを一度でも通ったか」という情報だけでは最終的に貧乏神がついてしまうかを確実に予測することはできず、「現在だれに貧乏神が付いているのか?」という情報を持っておく必要があります。
最終的に貧乏神が付かない移動方法 ~貧乏神がついていない場合~ (2020/12/21 追記)
自分に貧乏神が付いていない場合に、移動後に貧乏神が付いていない状態となるための方法として、貧乏神を持つ他のプレイヤーと移動中に接触しないという方法が思いつきます。そうすれば移動中に自分に貧乏神が付くことは一度もなく、最終的に貧乏神が付かずに希望の移動先へ移動することができます。そしてまた、貧乏神を持つ他のプレイヤーと接触しても、移動中に別のプレイヤーになすりつけたり、盤面の閉路をぐるぐる回ることで元々貧乏神を持っていたプレイヤーに付け返すことでも、最終的に貧乏神が付かずに希望の移動先へ移動することができます。前者の「貧乏神を持つプレイヤーと接触しない」という可能性の考慮だけで良ければ、貧乏神を考慮しない「いけるかな」の盤面上で、貧乏神を持つプレイヤーがいるマスを存在しないマスとして扱うことでも実現できます。しかし、いちど自分に付いた貧乏神をなすりつけ返すことでという行動も桃鉄においては常套手段であり、貧乏神が付いてしまうかどうかを確実に予測するためにはこれも考慮に入れるべきです。そのため、こちらの場合においても「現在だれに貧乏神が付いているのか?」という情報を持っておく必要があります。
愚直な幅優先探索
さて、それでは具体的な実装を考えてみましょう。貧乏神を考慮した「いけるかな」は「現在誰に貧乏神が付いているのか」の情報がキモとなるので、幅優先探索の際の状態として貧乏神を考慮しない場合にも使用している、「残り移動可能ステップ数」, 「現在いるノードのid」, 「直前に通ったノードの情報」に加えて「現在誰に貧乏神が付いているのか」の状態を持たせて幅優先探索を行います。幅優先探索の探索を行う場面では、自分に貧乏神がついているか否か や、移動先のマスに貧乏神を持つプレイヤーがいるか否か によって分岐を行っています。以下にそのプログラムを添付します。GitHub上の対応するコードは こちらです。
なお、ここでは移動先のマスにどのプレイヤーがいるかを調べるためにwhichPlayersOn関数を使用しています。whichPlayersOn関数の実装についてはGitHub上のこちらにあります。
このアルゴリズムでは「貧乏神が付いているプレイヤー」の状態が増えるため、貧乏神を考慮しない場合に比べて処理が定数倍重くなりますが、計算量は変わらずO(4^D)です。
const std::array<std::set<int>, 2> solveBruteForce(const std::vector<std::vector<int>>& Graph, const std::vector<int>& players_pos, const int& BONBI_playler_id, const int& DICE_NUM, const int& MAP_NUM) {
if (BONBI_playler_id < 0 or BONBI_playler_id >= (int)players_pos.size()) {
std::cout << "Invalid BONBI_player_id. " << BONBI_playler_id << std::endl;
return {};
}
if (DICE_NUM == 0) {
return {std::set<int>{players_pos[0]}, std::set<int>{players_pos[0]}};
} else if (DICE_NUM < 0) {
std::cout << "DICE_NUM is less than 0 ??? ( " << DICE_NUM << " )" << std::endl;
return {};
}
const int MY_PLAYER_ID = 0;
const int NO_BONBI = 0;
const int WITH_BONBI = 1;
std::array<std::set<int>, 2> reachable_nodes;
const std::vector<std::vector<char>> direction_table = getDirectionTable(Graph);
std::queue<BFS_Status_with_bonbi> que;
que.push(BFS_Status_with_bonbi{DICE_NUM, players_pos[0], NON_DIRECTION, BONBI_playler_id});
while(not que.empty()) {
const BFS_Status_with_bonbi que_front = que.front();
que.pop();
assert(Graph[que_front.node_num].size() <= 4);
if ((int)que_front.remaining_move <= 0) {
assert((int)que_front.remaining_move == 0);
if (que_front.player_with_BONBI_id == MY_PLAYER_ID) {
reachable_nodes[WITH_BONBI].insert(que_front.node_num);
} else {
reachable_nodes[WITH_BONBI].insert(que_front.node_num);
reachable_nodes[NO_BONBI ].insert(que_front.node_num);
}
} else {
for (const int& dist_node: Graph[que_front.node_num]) {
if (direction_table[que_front.node_num][dist_node] == que_front.direction) continue;
int new_player_with_BONBI_id;
const std::vector<int> the_player_ids = whichPlayersOn(dist_node, players_pos);
const bool does_anyone_on_dist_node_has_BONBIE = isVectorIncludesTheID(the_player_ids, que_front.player_with_BONBI_id);
if (the_player_ids.empty() or (not does_anyone_on_dist_node_has_BONBIE and MY_PLAYER_ID != que_front.player_with_BONBI_id)) {
// 無人のマスへの移動 or 自分もそのマスのプレイヤーも貧乏神を持たない場合の移動
new_player_with_BONBI_id = que_front.player_with_BONBI_id;
} else if (does_anyone_on_dist_node_has_BONBIE) { // 移動先のマスに貧乏神を持っているプレイヤーがいる
new_player_with_BONBI_id = MY_PLAYER_ID;
} else if (MY_PLAYER_ID == que_front.player_with_BONBI_id and not the_player_ids.empty()) { // 自分が貧乏神を持っていて移動先に他のプレイヤーがいる
new_player_with_BONBI_id = the_player_ids[0];
} else { // 空集合
std::cout << "Something is wrong if you reached here." << std::endl;
exit(1);
}
que.push(BFS_Status_with_bonbi{que_front.remaining_move-1, dist_node, direction_table[dist_node][que_front.node_num], new_player_with_BONBI_id});
}
}
}
return reachable_nodes;
}
幅優先探索をメモ化
こちらの幅優先探索も、貧乏神を考慮しない場合と同様にメモ化して効率化することができます。dp[dice_sum][map_squares_num][direction][player_with_BONBI]を状態とし、その状態がすでに探索済みであればtrue、そうでなければfalseを持つことにします。以下にそのプログラムを添付します。GitHub上の対応するコードは こちらです。
メモ化した場合も同様に計算量は変わらず、O(min(D^3, DM))で解くことができます。
const std::array<std::set<int>, 2> solveIkerukanaDP(const std::vector<std::vector<int>>& Graph, const std::vector<int>& players_pos, const int& BONBI_playler_id, const int& DICE_NUM, const int& MAP_NUM) {
if (BONBI_playler_id < 0 or BONBI_playler_id >= (int)players_pos.size()) {
std::cout << "Invalid BONBI_player_id. " << BONBI_playler_id << std::endl;
return {};
}
if (DICE_NUM == 0) {
return {std::set<int>{players_pos[0]}, std::set<int>{players_pos[0]}};
} else if (DICE_NUM < 0) {
std::cout << "DICE_NUM is less than 0 ??? ( " << DICE_NUM << " )" << std::endl;
return {};
}
const int MY_PLAYER_ID = 0;
const int NO_BONBI = 0;
const int WITH_BONBI = 1;
std::array<std::set<int>, 2> reachable_nodes;
const std::vector<std::vector<char>> direction_table = getDirectionTable(Graph);
bool dp[DICE_NUM+1][MAP_NUM][DIRECTION_NUM][MAX_PLAYERS_NUM];
memset(dp, 0, sizeof(dp));
std::queue<BFS_Status_with_bonbi> que;
que.push(BFS_Status_with_bonbi{DICE_NUM, players_pos[0], NON_DIRECTION, BONBI_playler_id});
while(not que.empty()) {
const BFS_Status_with_bonbi que_front = que.front();
que.pop();
assert(Graph[que_front.node_num].size() <= 4);
if ((int)que_front.remaining_move <= 0) {
assert((int)que_front.remaining_move == 0);
if (que_front.player_with_BONBI_id == MY_PLAYER_ID) {
reachable_nodes[WITH_BONBI].insert(que_front.node_num);
} else {
reachable_nodes[WITH_BONBI].insert(que_front.node_num);
reachable_nodes[NO_BONBI ].insert(que_front.node_num);
}
} else {
for (const int& dist_node: Graph[que_front.node_num]) {
if (direction_table[que_front.node_num][dist_node] == que_front.direction) continue;
int new_player_with_BONBI_id;
const std::vector<int> the_player_ids = whichPlayersOn(dist_node, players_pos);
const bool does_anyone_on_dist_node_has_BONBIE = isVectorIncludesTheID(the_player_ids, que_front.player_with_BONBI_id);
if (the_player_ids.empty() or (not does_anyone_on_dist_node_has_BONBIE and MY_PLAYER_ID != que_front.player_with_BONBI_id)) {
// 無人のマスへの移動 or 自分もそのマスのプレイヤーも貧乏神を持たない場合の移動
new_player_with_BONBI_id = que_front.player_with_BONBI_id;
} else if (does_anyone_on_dist_node_has_BONBIE) { // 移動先のマスに貧乏神を持っているプレイヤーがいる
new_player_with_BONBI_id = MY_PLAYER_ID;
} else if (MY_PLAYER_ID == que_front.player_with_BONBI_id and not the_player_ids.empty()) { // 自分が貧乏神を持っていて移動先に他のプレイヤーがいる
new_player_with_BONBI_id = the_player_ids[0];
} else { // 空集合
std::cout << "Something is wrong if you reached here." << std::endl;
exit(1);
}
bool& dp_target_elm = dp[que_front.remaining_move-1][dist_node][(size_t)direction_table[dist_node][que_front.node_num]][new_player_with_BONBI_id];
if (not dp_target_elm) {
que.push(BFS_Status_with_bonbi{que_front.remaining_move-1, dist_node, direction_table[dist_node][que_front.node_num], new_player_with_BONBI_id});
dp_target_elm = true;
}
}
}
}
return reachable_nodes;
}
なぜ貧乏神を考慮した「いけるかな」が桃鉄に実装されていないのか
ここまでは、貧乏神を考慮しない「いけるかな」と貧乏神を考慮した「いけるかな」について考察し、実装を紹介しました。貧乏神を考慮することによってやや実装は複雑になりましたが、考え方としてはどちらも大きく変わらないことがわかりました。しかしながら桃鉄には前者の「いけるかな」+α(断言しない貧乏神チェック)しか実装されていません。その理由について以下で私の考察を述べます。
仮説1: 貧乏神を考慮した「いけるかな」は幅優先探索のなかでもやや応用的であるから?
プログラムの分量や幅優先探索を行うwhile文内の処理量を見ると、貧乏神を考慮しない「いけるかな」の方はシンプルな幅優先探索と言えます。一方、貧乏神を考慮した場合の幅優先探索は「貧乏神が誰に付いているか?」といういわば盤面や他プレイヤーなど、移動するプレイヤー自身以外の状態が変化する幅優先探索と言うことができます。この記事の内容を難なく理解できるような、研究や競技プログラミングなどにおいて普段からグラフアルゴリズムに触れている人にとってはどちらのアルゴリズムも大差なく、大して複雑でないと感じるかと思います。実際、競技プログラミングのコンテストを開催するAtCoderなどで出題されれば、青色コーダー以上(日本に3000人くらいいます)のRatingを持つ出場者のほとんどは、数時間もあれば難なく解いてしまうんじゃないでしょうか。しかしながら、今回の幅優先探索のような汎用的なアルゴリズムを実際の問題に適用して応用的な問題を解くことは、ある程度の訓練なしには容易ではないと言うこともご理解いただけると思います。そして、このような訓練をつんだプログラマが偶然桃鉄の開発チームにはいなかったという可能性は十分にあるでしょう。
仮説2: 貧乏神を考慮しない「いけるかな」だけでも実行時間がキツキツだった?
それぞれの「いけるかな」のアルゴリズムの実行時間を計測するため、今回テストプログラムの作成とテスト用盤面データの生成を行いました。「貧乏神が付くか否かを確実に予測」するアルゴリズムのテストプログラムの詳細はGitHub上のこちらを参照、テスト用マップデータ生成用プログラムの詳細はGitHub上のこちらを参照して下さい。
ここでは、最悪ケースとして900頂点674(=900*0.75)辺のグリッドグラフを盤面として使用し、出目を48とした場合のメモ化幅優先探索アルゴリズムの実行時間を計測しました(テストプログラム中のDPExecuteLarge1というテストに対応します)。私の使用しているCPU、AMD Ryzen5 3400GEのシングルコアで実行した結果、5度実行した際の平均実行時間は以下のようになりました。
| アルゴリズム | 実行時間[ms] | 考慮なしの場合との実行時間比[倍] |
|---|---|---|
| 貧乏神を考慮しないメモ化幅優先探索 | 16 | - |
| 貧乏神を考慮したメモ化幅優先探索 | 27 | 1.69 |
実際の桃鉄の盤面は今回用意した盤面ほど密ではなく、またグラフの木幅も小さいため、実際のゲーム内の盤面上での処理を私のCPUで実行した際の実行時間はもう少し短くなることが予想されます。しかしながら、桃鉄が動作するゲーム機の計算性能は必ずしもコンピュータのCPUほど高くありません。Switch版の「いけるかな」と同様の機能が初めて搭載された桃鉄16(本作では同様の機能が「いけますよ!」という名前で実装されている)は、PS2やWiiなど、家庭用ゲーム機で発売されているシリーズです。ここで、計算性能を測る指標の一つである浮動小数点演算性能(FLOPS)を用いて、コンピュータと家庭用ゲーム機の性能を比較してみましょう。PS2のプロセッサの浮動小数点演算性能はwikipediaによると6.2GFLOPS、一般的なコンピュータのシングルスレッド性能は数十GFLOPS程度のようです。これを手がかりにすると、ゲーム機での「いけるかな」機能の実行は、単純計算で私のPCでの実行の数倍から十数倍の実行時間がかかることが予想できます。ゲームプログラミングにおいて「いけるかな」のような処理にどれくらいの実行時間がかかることを許容できるのかはわかりませんが、例えば100ms(16msの6.25倍)くらいの実行時間になってくると、体感できるレベルのラグがプレイ中に発生するのはないでしょうか。つまり、貧乏神を考慮しない「いけるかな」の時点で結構キツキツの実行時間だったのではないかと想像することができます。このことから、桃鉄に「貧乏神が付くか否かを確実に予測」する機能が付かなかったのは、ゲーム本編の安定動作のために機能を削った結果と予想することもできます。
また、桃鉄16(Switch版の「いけるかな」と同様の機能が初めて搭載された)について語っている月刊デジタルさくまにあ:桃鉄研究所にゲーム機の性能がネックになったことを示す以下の記述が見つかりました。この さくま という方は桃鉄の最強COMであるさくまの由来にもなっている、開発者の佐久間 晃(さくま あきら)さんですね。
<いけますよ!>に感動しました。
これは便利すぎます…。
どこの物件駅に行こうか、迷ってしまいますね~。
出石か…奈良か…。どっちにしようとか。
すごく便利ですが、どう考えても能力の高いハードじゃなきゃできま
せんね。
●さくま「DSでも無理なんだよ、この機能!」
確か『スーパー桃鉄2』ではじめて、<いけるかな!>が搭載された
時も感動したんですよね~。
でも大きい数だして、<いけるかな>すると、考え込んじゃって、し
ばらく動かなかったんですよね。
技術の進歩はすばらしいなぁ!
●さくま「あの考え込むやつだって、ハドソンの高い技術力だから、あ
の速さで可能だったのだ。ほかのメーカーだったら、<いけますよ>自
体無理のひとことで終わっていたとおもう!」
さくまさんのコメントによると、DSでは「いけますよ!」(Switch版の「いけるかな」と同様の機能)が実現できず、PS2やWiiなどの家庭用ゲーム機で発売された桃鉄16でなんとか実現できたということがわかります。つまり、少なくとも当時の「いけますよ」は、DSでは負荷が大きすぎるが、PS2などのゲーム機ではなんとか処理可能なレベルのアルゴリズムであったと推測できます。DSの浮動小数点演算性能に関する記述を見つけられなかったのでCPUの動作クロックによる雑な比較をすると、DSのCPUクロックが67MHz, PS2のCPUクロックが294MHzとなっており、性能向上は数倍~十数倍程度であることが予想できます(だいぶ雑な比較なのでやや怪しいですが)つまりその程度のプロセッサ性能の変化によって実現できたりできなかったりするアルゴリズムであることを読み取ることができ、実行時間的に結構キツキツの機能であるという考察に現実味が増しました。
まとめ
貧乏神を考慮しない場合の「いけるかな」と貧乏神を考慮した場合の「いけるかな」に対して、それぞれシンプルな幅優先探索の実装を紹介し、その後メモ化による効率的な実装を紹介した。その後、これらの実装の比較や最悪ケースの実行時間の比較を行うことにより、「貧乏神が付くか否かを確実に予測」する「いけるかな」の機能が桃鉄に実装されていない理由を考察した。
※ ここでの考察は筆者の桃鉄プレイ経験やweb上の記事のみを参考にして作成されました。実際の開発者の考えなどとは大幅に異なる場合があります。
PS2での実行時間に関する考慮について (2020/12/21)
家庭用PCでの実行時間からPS2での実行時間を予想するために、記事内ではFLOPSという指標を使用しました。しかしながら本アルゴリズムは浮動小数点演算を行っておらず、あまり適切ではありません。そのため、以下に単位時間あたりの命令実行数を表すMIPS(Mega Instructions Per Sec)を指標として実行時間の予測を行った結果に関する考察を追加します。(なお、記事内で決して適切とは言えないFLOPSで比較している理由は、執筆時はAdventCalendarの締め切りに追われており、FLOPSが一番手っ取り早い情報だと考えたためです......)
ゲーム機の製品イノベーションにおける位置取り問題の13ページ目にある各ゲーム機のスペックの表を参考にするとPS2が435MIPS、実験に使用したR5 3400GEのシングルコア性能がおそらく4万MIPS前後であるため、PS2では実験値の100倍近い時間がかかる可能性も十分あります。