この記事はデータ構造とアルゴリズム Advent Calendar 2020 17日目の記事です。
タイトルが小難しそうに見えますがサッと読めます。
はじめに
みなさんは「最適化問題の解がたくさんほしい!」と思ったことはありますか?
ありませんね 〜完〜
というわけにもいかないので続けますが、最適化問題の解を複数得ることには実用上のメリットがあります。
よく言われるのが、最適化問題はあくまで現実の問題をモデル化したものであり、その最適解が現実で本当に良いものであるか、そもそも現実の制約を満たすかは不確実であるということです。
そこで、複数の解を得ておけば現実に則した良い解を得られる可能性が高まるわけですね。
最適化問題やら複数の解やらと一口に言っても色々ありますが、本記事では(解を 0-1 ベクトルで表現可能な)離散最適化問題の上位 $K$ 個の解に着目し、それらを列挙する一般的な枠組みを紹介します。
この枠組みは Lawler's $K$-Best Solutions 1 と呼ばれており、サイズ $n$ の問題を解くのにかかる計算時間を $O(c(n))$ として $O(Knc(n))$ 時間で動作します。
本記事で扱う問題
変数の個数 $n$ と制約 $C$ および目的関数 $f: \{0,1\}^n \rightarrow \mathbb{R}$ に対して、$C$ を満たす変数割当て $x = (x_1, x_2, \ldots, x_n) \in \{0,1\}^n$ の中で $f(x)$ を最大(あるいは最小)にする $x$ を見つける問題を考えます。
ナップサック問題や最短経路問題、最小全域木問題など様々な問題がこの形で記述できます。
Lawler's K-Best Solutions
Lawler's $K$-Best Solutions は、所与の問題の厳密解法をサブルーチンとして、目的関数値が良い順(最大化問題ならば降順、最小化問題ならば昇順)に $K$ 個の解を列挙します。
このアルゴリズムを理解するには、次節で説明する解空間の分割をイメージできるようになれば十分です。
解空間の分割
今、所与の問題の最適解、すなわち1番目に良い解を $x' \in \{0,1\}^n$ とします。
$n$ 個の変数になんらかの順序 $i_1, i_2, \ldots, i_n$ を付けます。
ここで、各 $1 \leq p \leq n$ について次のように変数を固定することを考えます。
x_{i_1} = x'_{i_1}, \ldots, x_{i_{p-1}} = x'_{i_{p-1}}, x_{i_p} = 1 - x'_{i_p}
$p$ に対する変数の固定により得られる解空間を $X^{(p)} \subset \{0,1\}^n$ とします。
このとき、$X^{(1)} \cap X^{(2)} \cap \cdots \cap X^{(n)} = \emptyset$ が成り立つほか、すべの $p$ について $x' \notin X^{(p)}$ が成り立ちます(イメージは下図のようになります)。
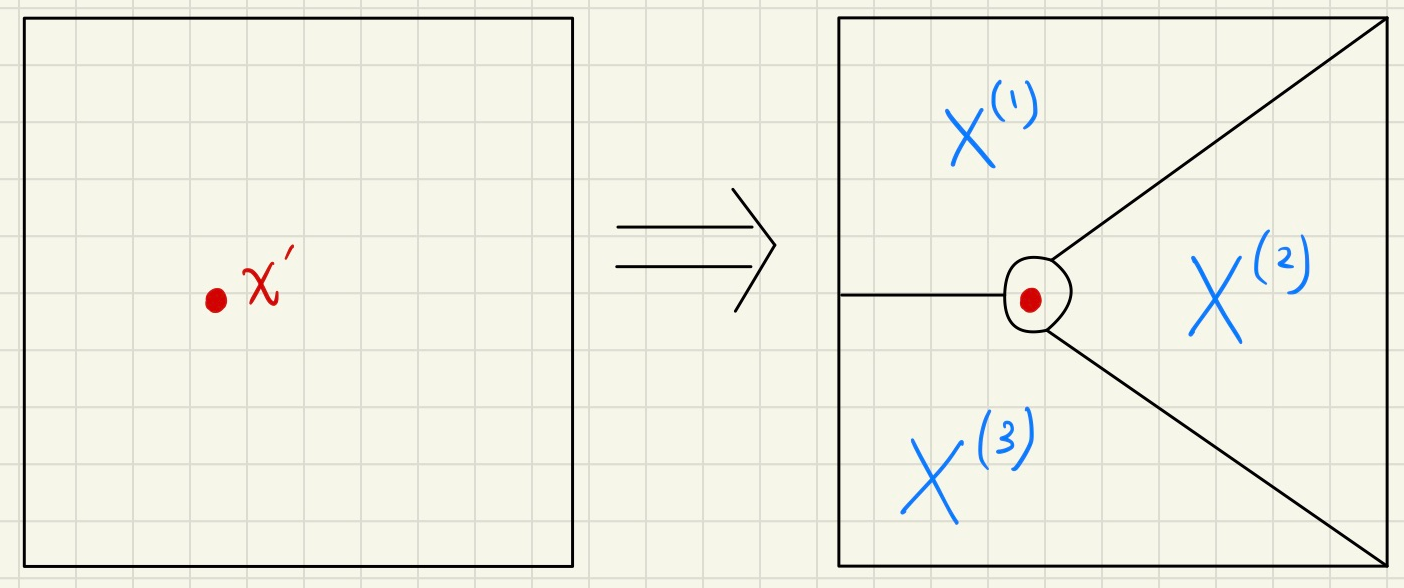
このことから、2番目に良い解は各 $X^{(p)}$ に限定して所与の問題を解いた中に存在することになります。
より一般的に考えると、実行可能解を持つ任意の解空間を、その中での最適解に従って変数を順に固定することで、元の最適解を持たず互いに素ないくつかの解空間に分割できるとわかります。
ここで、変数を固定する順序には任意性があることに注意してください。
アルゴリズム
Lawler's $K$-Best Solutions は全体の最適解の求解から開始して、解空間の分割と各解空間に限定した求解を繰り返すことで、目的関数値の良い順に解を出力します。
アルゴリズムはヒープを用いて、ある解 $x'$ と固定した変数の集合 $F \subseteq \{1,2,\ldots,n\}$ からなるペア $(x',F)$ を $f(x')$ の値が良い順に管理します。
アルゴリズムの手順は以下のとおりです。
-
- ヒープを全体の最適解と $F = \emptyset$ のペアのみで初期化する。
-
- $K$ 個の解が出力されるまで以下を繰り返す。
- 2-1. 先頭のペア $(x',F)$ をヒープからポップし $x'$ を出力する。
- 2-2. 固定されていない各変数 $i \notin F$ に適当な順序 $i_{|F|+1}, i_{|F|+2}, \ldots, i_n$ を付ける(固定済みの変数は適当に $i_1, i_2, \ldots, i_{|F|}$ とする)。
- 2-3. 各 $|F|+1 \leq p \leq n$ について、前述の要領で $X^{(p)}$ を考える。
- 2-4. $X^{(p)}$ が実行可能解をもつならば、その最適解 $x''$ を求め $(x'', F \cup \{i_{|F|+1}, \ldots i_p\})$ をヒープにプッシュする。
このとき、$k$ 番目に出力された解が $k$ 番目に良い解になっています。
2-2 および 2-4 の処理を問題や解法に応じて設計する必要があることには注意してください。
Lawler's $K$-Best Solutions の動作は下図のようにイメージできます。
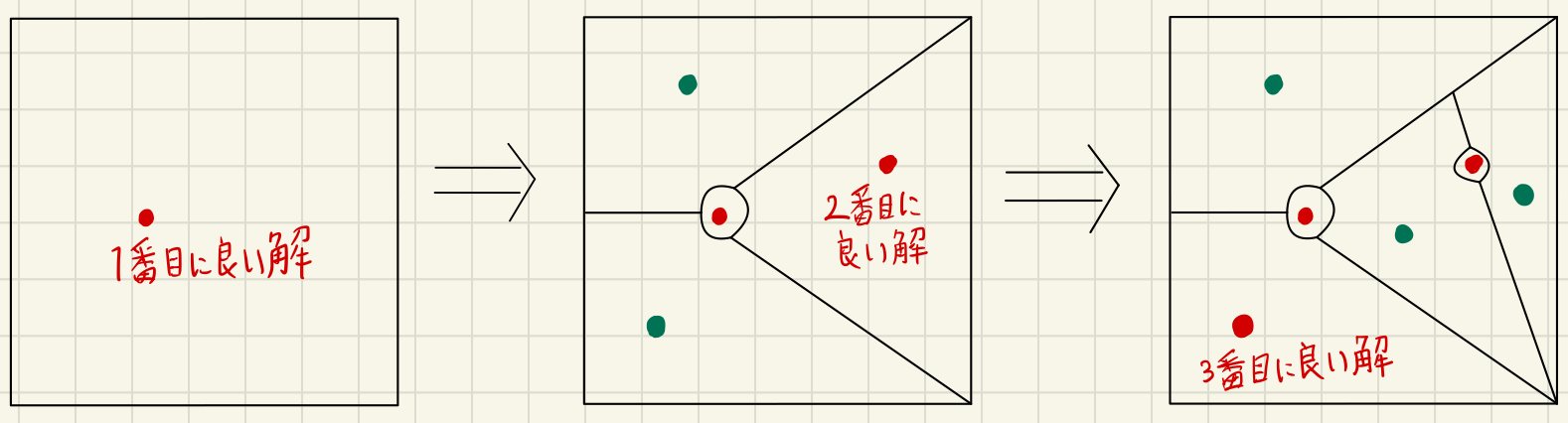
実線で囲まれた各領域が解空間を表し、各点がヒープに保持されている解を表します。
赤い点がポップされた解です。
最後に Lawler's $K$-Best Solutions の計算時間を確認します。
ポップされたペア1つにつき、最大で $n$ 個の解空間を生成しそれぞれで求解します。
これを $K$ 個のペアがポップされるまで繰り返すことと、ヒープの操作は求解より十分高速にできることから、Lawler's $K$-Best Solutions は求解にかかる計算時間を $O(c(n))$ として $O(Knc(n))$ 時間で動作します。
例
Lawler's $K$-Best Solutions を動かすには、変数を固定する順序の決め方と、一部の変数を固定した状態で所与の問題を(効率よく)解く厳密解法が必要になります。
ここでは、変数を固定する順序と厳密解法の設計について、いくつかの例を簡単に紹介します。
ただし、すでに問題概要と基本的な厳密解法を知っている人向けです。
ナップサック問題
$n$ 個のアイテムがあり $x_i = 1$ であることとアイテム $i$ を取ることが対応付くと考えます。
効率よい厳密解法として、動的計画法がよく知られていますね。
ナップサック問題では変数を固定する順序は任意でよく、一部の変数が固定されいるときの厳密解法は次のように考えればよいです。
- $x_i = 0$ で固定されているアイテム $i$ を削除する。
- $x_i = 1$ で固定されているアイテム $i$ はすでに取ったものとしナップサックの容量を減らす。
- このとき、すでに容量が足りていなければ実行可能解は存在しない。
- 変数が固定されていないアイテムと残りの容量の上で動的計画法を実行する。
最短経路問題
$n$ 本の辺があり $x_i = 1$ であることと辺 $i$ を経路に含めることが対応付くと考えます。
効率よい厳密解法として、ダイクストラ法がよく知られていますね。
最短経路問題では、変数を固定する順序は少しトリッキーです。
ある解 $x'$ に従って変数を固定するときは、始点から終点へ向かって「$x'$ が示す経路上の辺をたどった順序」を変数を固定する順序とします。
これにより、始点に近い方から順に経路に含まれる辺が固定されていきます。
一部の変数が固定されいるときの厳密解法は次のように考えればよいです。
- $x_i = 0$ で固定されている辺 $i$ を削除する。
- 辺の削除により始点と終点が非連結になった場合は実行可能解が存在しない。
- $x_i = 1$ で固定されている辺からなる部分グラフが、始点からいずれかの頂点への経路を成していなければ実行可能解は存在しない。
- その経路を始点からたどって行き着いた頂点をあらたな始点とする。
- $x_i = 1$ で固定されている辺 $i$ に接続する頂点(新たな始点を除く)を削除する。
- 変形したグラフの上でダイクストラを実行する。
最小全域木問題
$n$ 本の辺があり $x_i = 1$ であることと辺 $i$ を木に含めることが対応付くと考えます。
効率よい厳密解法として、クラスカル法やプリム法がよく知られていますね。
最小全域木問題では変数を固定する順序は任意でよく、一部の変数が固定されいるときの厳密解法は次のように考えればよいです。
- $x_i = 0$ で固定されている辺 $i$ を削除する。
- 辺の削除によりグラフが非連結になった場合は実行可能解が存在しない。
- $x_i = 1$ で固定されている辺からなる部分グラフが閉路を持つならば実行可能解が存在しない。
- $x_i = 1$ で固定されている辺 $i$ を縮約する。
辺の縮約により自己ループが発生した場合は実行可能解が存在しない。- 変形したグラフの上で貪欲法を実行する。
辺の縮約を考慮すると、Union-Find を用いるクラスカル法の方が扱いやすそうですね。
終わりに
Lawler's $K$-Best Solutions は、変数を固定する順序や厳密解法をうまく設計する必要がありますが、それ以外は単純なアルゴリズムです。
こんなに簡単に上位 $K$ 個の解が列挙できちゃうんですね。
みなさんは「最適化問題の解がたくさんほしい!」と思えましたか?
本記事を読んだだけではそうでもないですよね 〜完〜