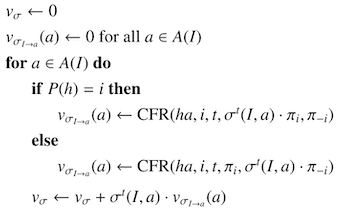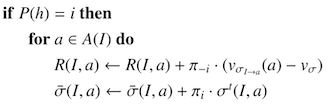OpenSpielで始める強化学習その② - 自作ゲームでCFRを実験 -

初めに

CFRが収束する様子

OpenSpielとは

DEEPMINDが作成した研究者向けの強化学習フレームワークのOSSです。マルチエージェントRLの研究の促進や研究の再現性の向上を目的としています。
主にPythonとC++で書かれていますが、Go、Juliaもサポートされています。
深層強化学習はTensorFlow1、2、JAXとPytorchに対応しています。
最近実験的にrustをサポートし始めているようです。

想定される読者

強化学習について勉強してみたいけどまずは動くものを作ってみたい！という人向けです。

今回の内容（3行まとめ）

• ばかなおうじさんの記事を参考にCFRの実装
• 状態数の少ないゲーム(kuhn_poker)での実験で実装が正しいかを確認
• 同時手番ゲーム(報酬が歪なジャンケン)を展開型ゲームとみたててopen_spiel上で作成し視覚的にも均衡に近づいていることを確認

動かしながら読み進めたい方はこちら(colab)
最終的な実装にだけ興味ある場合はこちら
open_spielで自作ゲームの作り方を知りたい方はこちら

環境

$ sw_vers
ProductName:    macOS
ProductVersion: 11.4
BuildVersion:   20F71

$ python3 -V
Python 3.9.9

CFRについて

理論

この記事では理論について一切触れません。
そのため理論が詳しく知りたいという方は、この記事で参考にさせていただいている
ばかなおうじさんの記事をご覧いただけると幸いです。

実装

ばかなおうじさんの記事にある疑似コードを確認しつつ、実装していきます。

前準備（ゲームを動かす）

まず初めにopen_spielでゲームを進めるための実装は下記でした。（過去記事①参照）

import pyspiel
import numpy as np


game = pyspiel.load_game('kuhn_poker')
state = game.new_initial_state()
while not state.is_terminal():
    legal_actions = state.legal_actions()
    if state.is_chance_node():
        outcomes_with_probs = state.chance_outcomes()
        action_list, prob_list = zip(*outcomes_with_probs)
        action = np.random.choice(action_list, p=prob_list)
        state.apply_action(action)
    else:
        legal_actions_mask = state.legal_actions_mask()
        prob_list = [
            legal_actions_mask[action] / sum(legal_actions_mask)
            for action in legal_actions
        ]
        action = np.random.choice(legal_actions, p=prob_list)
        state.apply_action(action)

この式を利用すると，ゲーム木の全ノードを一回ずつ辿るだけで，全ての情報集合に対するcounterfactual valueを計算することができます．以下の擬似コードはCFRのアルゴリズムであり，この擬似コードでも再帰的にvalueの計算を行っています．

参考記事内でも書かれている通り、擬似コードでは再帰的に処理を行うことで効率化をしています。
まず上記を再帰的に実行できるように変更します。

import pyspiel
import numpy as np


game = pyspiel.load_game('kuhn_poker')
ini_state = game.new_initial_state()
def cfr(state):
    if state.is_terminal():
        return state.returns()
    elif state.is_chance_node():
        outcomes_with_probs = state.chance_outcomes()
        action_list, prob_list = zip(*outcomes_with_probs)
        action = np.random.choice(action_list, p=prob_list)
        state.apply_action(action)
        return cfr(state)
    else:
        legal_actions = state.legal_actions()
        legal_actions_mask = state.legal_actions_mask()
        prob_list = [
            legal_actions_mask[action] / sum(legal_actions_mask)
            for action in legal_actions
        ]
        action = np.random.choice(legal_actions, p=prob_list)
        state.apply_action(action)
        return cfr(state)
cfr(ini_state)

以降はこちらを基にして進めていきます。

ターミナルノードとチャンスノード

• ターミナルノード
  • プレイヤーの利得が返り値
• チャンスノード
  • チャンスプレイヤーの行動確率 * cfr関数の返り値をノードで実行可能な行動の全ての場合を足し合わせたものが返り値

上記を反映してみると下記になります。

import pyspiel
import numpy as np


game = pyspiel.load_game('kuhn_poker')
ini_state = game.new_initial_state()
def cfr(state, player_id, my_reach, opponent_reach):
    if state.is_terminal():
        return state.returns()[player_id]
    elif state.is_chance_node():
        outcomes_with_probs = state.chance_outcomes()
        v = 0
        for a, prob in outcomes_with_probs:
            v += prob * cfr(state.child(a), player_id, my_reach, prob * opponent_reach)
        return v
    else:
        legal_actions = state.legal_actions()
        legal_actions_mask = state.legal_actions_mask()
        prob_list = [
            legal_actions_mask[action] / sum(legal_actions_mask)
            for action in legal_actions
        ]
        action = np.random.choice(legal_actions, p=prob_list)
        state.apply_action(action)
        return cfr(state, player_id, my_reach, opponent_reach)
cfr(ini_state, 0, 1.0, 1.0)

ここでは、同じstateに異なるactionを実行して欲しいためstate.child(action)を使用しています。
state.apply_action(action)ではstateが先に進んでしまい戻す必要がでてきます。

ターミナルノードでどちらのプレイヤーの利得を返すか決めるためにcfr関数にplayer_idという引数が増えました。
またチャンスノードで対戦相手の到着確率にチャンスノードでの行動確率をかけるので引数を追加しています。

プレイヤーノード

ポリシーの更新（リグレットマッチング）

リグレットマッチングに関して詳しい説明している記事はこちらが参考になると思います。
反復数tがでてきていますが一旦無視しましょう。

from collections import defaultdict

import pyspiel
import numpy as np


game = pyspiel.load_game('kuhn_poker')
ini_state = game.new_initial_state()
cum_regrets = defaultdict(lambda: np.zeros(game.num_distinct_actions()))
def cfr(state, player_id, my_reach, opponent_reach):
    if state.is_terminal():
        return state.returns()[player_id]
    elif state.is_chance_node():
        outcomes_with_probs = state.chance_outcomes()
        v = 0
        for a, prob in outcomes_with_probs:
            v += prob * cfr(state.child(a), player_id, my_reach, prob * opponent_reach)
        return v
    else:
        legal_actions = state.legal_actions()
        legal_actions_mask = np.array(state.legal_actions_mask())
        state_string = state.information_state_string()
        state_regret = np.maximum(cum_regrets[state_string], 0)
        policy = np.zeros(game.num_distinct_actions())
        if state_regret.sum() > 0:
            regret_matching_policy = state_regret / state_regret.sum()
            for a in legal_actions:
                policy[a] = regret_matching_policy[a]
        else:
            policy = legal_actions_mask / legal_actions_mask.sum()
        action = np.random.choice(legal_actions, p=policy)
        state.apply_action(action)
        return cfr(state, player_id, my_reach, opponent_reach)
cfr(ini_state, 0, 1.0, 1.0)

Counter factual valueの計算

ここで先ほど無視していた反復数tが異なるポリシーが出てくるのでその対応もします。

from collections import defaultdict

import pyspiel
import numpy as np


game = pyspiel.load_game('kuhn_poker')
ini_state = game.new_initial_state()
n_actions = game.num_distinct_actions()
cum_regrets = defaultdict(lambda: np.zeros(n_actions))
policies = []
policies.append(defaultdict(lambda: np.ones(n_actions) / n_actions))
def cfr(state, player_id, epoch, my_reach, opponent_reach):
    if state.is_terminal():
        return state.returns()[player_id]
    elif state.is_chance_node():
        outcomes_with_probs = state.chance_outcomes()
        v = 0
        for a, prob in outcomes_with_probs:
            v += prob * cfr(state.child(a), player_id, epoch, my_reach, prob * opponent_reach)
        return v
    else:
        legal_actions = state.legal_actions()
        legal_actions_mask = np.array(state.legal_actions_mask())
        state_string = state.information_state_string()
        if len(policies) <= (epoch + 1):
            policies.append(defaultdict(lambda: np.ones(n_actions) / n_actions))
        state_regret = np.maximum(cum_regrets[state_string], 0)
        if state_regret.sum() > 0:
            regret_matching_policy = state_regret / state_regret.sum()
            for a in legal_actions:
                policies[epoch + 1][state_string][a] = regret_matching_policy[a]
        else:
            policies[epoch + 1][state_string] = legal_actions_mask / legal_actions_mask.sum()
        v = 0
        v_counter_factual = np.zeros(game.num_distinct_actions())
        for a in legal_actions:
            if state.current_player() == player_id:
                v_counter_factual[a] = cfr(state.child(a), player_id, epoch, policies[epoch][state_string][a] * my_reach, opponent_reach)
            else:
                v_counter_factual[a] = cfr(state.child(a), player_id, epoch, my_reach, policies[epoch][state_string][a] * opponent_reach)
            v += policies[epoch][state_string][a] * v_counter_factual[a]
        action = np.random.choice(legal_actions, p=policies[epoch][state_string])
        state.apply_action(action)
        return cfr(state, player_id, epoch, my_reach, opponent_reach)
cfr(ini_state, 0, 0, 1.0, 1.0)

policiesが再起的な処理中に何度もappendされないように、一旦不恰好ですがpoliciesのlengthでappendを制御しています。

累積リグレットと平均戦略の更新

擬似コード内のSolve関数も一緒に実装することで、先ほど不恰好のまま残していた部分もここで修正します。

from collections import defaultdict

import pyspiel
import numpy as np


game = pyspiel.load_game('kuhn_poker')
n_actions = game.num_distinct_actions()
cum_regrets = defaultdict(lambda: np.zeros(n_actions))
cum_strategies = defaultdict(lambda: np.zeros(n_actions))
policies = []
policies.append(defaultdict(lambda: np.ones(n_actions) / n_actions))
def cfr(state, player_id, epoch, my_reach, opponent_reach):
    if state.is_terminal():
        return state.returns()[player_id]
    elif state.is_chance_node():
        outcomes_with_probs = state.chance_outcomes()
        v = 0
        for a, prob in outcomes_with_probs:
            v += prob * cfr(state.child(a), player_id, epoch, my_reach, prob * opponent_reach)
        return v
    else:
        legal_actions = state.legal_actions()
        legal_actions_mask = np.array(state.legal_actions_mask())
        state_string = state.information_state_string()
        state_regret = np.maximum(cum_regrets[state_string], 0)
        if state_regret.sum() > 0:
            regret_matching_policy = state_regret / state_regret.sum()
            for a in legal_actions:
                policies[epoch + 1][state_string][a] = regret_matching_policy[a]
        else:
            policies[epoch + 1][state_string] = legal_actions_mask / legal_actions_mask.sum()
        v = 0
        v_counter_factual = np.zeros(game.num_distinct_actions())
        for a in legal_actions:
            if state.current_player() == player_id:
                v_counter_factual[a] = cfr(state.child(a), player_id, epoch, policies[epoch][state_string][a] * my_reach, opponent_reach)
            else:
                v_counter_factual[a] = cfr(state.child(a), player_id, epoch, my_reach, policies[epoch][state_string][a] * opponent_reach)
            v += policies[epoch][state_string][a] * v_counter_factual[a]
        if state.current_player() == player_id:
            for a in legal_actions:
                cum_regrets[state_string][a] += opponent_reach * (v_counter_factual[a] - v)
                cum_strategies[state_string][a] += my_reach * policies[epoch][state_string][a]
        return v


T = 100
for t in range(T):
    policies.append(defaultdict(lambda: np.ones(n_actions) / n_actions))
    for i in range(game.num_players()):
        ini_state = game.new_initial_state()
        cfr(ini_state, i, t, 1, 1)

平均戦略の評価

今のままだと辞書型でcumulative starategyを持っているだけですので、
open_spielでも簡単に使いまわせるものにしたいです。
今回は、公式が用意しているPolicyクラスを継承して変換していきます。

from open_spiel.python import policy

class AveragePolicy(policy.Policy):
    def __init__(self, game, player_ids, cum_strategy):
        super().__init__(game, player_ids)
        self.game = game
        self.cum_strategy = cum_strategy

    def action_probabilities(self, state, player_id=None):
        if player_id is None:
            player_id = state.current_player()
        legal_actions_mask = np.array(state.legal_actions_mask())
        tmp_policy = self.cum_strategy[state.information_state_string()]
        if tmp_policy.sum() > 0:
            tmp_policy = tmp_policy / tmp_policy.sum()
        else:
            tmp_policy = legal_actions_mask / legal_actions_mask
        return {i: tmp_policy[i] for i in range(self.game.num_distinct_actions())}

これで公式が用意している評価関数も簡単に使用できるようになりました。

完成!

from collections import defaultdict

import pyspiel
import numpy as np
from open_spiel.python import policy
from open_spiel.python.algorithms import expected_game_score, exploitability

game = pyspiel.load_game('kuhn_poker')
n_actions = game.num_distinct_actions()
cum_regrets = defaultdict(lambda: np.zeros(n_actions))
cum_strategies = defaultdict(lambda: np.zeros(n_actions))
policies = []
policies.append(defaultdict(lambda: np.ones(n_actions) / n_actions))
def cfr(state, player_id, epoch, my_reach, opponent_reach):
    if state.is_terminal():
        return state.returns()[player_id]
    elif state.is_chance_node():
        outcomes_with_probs = state.chance_outcomes()
        v = 0
        for a, prob in outcomes_with_probs:
            v += prob * cfr(state.child(a), player_id, epoch, my_reach, prob * opponent_reach)
        return v
    else:
        legal_actions = state.legal_actions()
        legal_actions_mask = np.array(state.legal_actions_mask())
        state_string = state.information_state_string()
        state_regret = np.maximum(cum_regrets[state_string], 0)
        if state_regret.sum() > 0:
            regret_matching_policy = state_regret / state_regret.sum()
            for a in legal_actions:
                policies[epoch + 1][state_string][a] = regret_matching_policy[a]
        else:
            policies[epoch + 1][state_string] = legal_actions_mask / legal_actions_mask.sum()
        v = 0
        v_counter_factual = np.zeros(game.num_distinct_actions())
        for a in legal_actions:
            if state.current_player() == player_id:
                v_counter_factual[a] = cfr(state.child(a), player_id, epoch, policies[epoch][state_string][a] * my_reach, opponent_reach)
            else:
                v_counter_factual[a] = cfr(state.child(a), player_id, epoch, my_reach, policies[epoch][state_string][a] * opponent_reach)
            v += policies[epoch][state_string][a] * v_counter_factual[a]
        if state.current_player() == player_id:
            for a in legal_actions:
                cum_regrets[state_string][a] += opponent_reach * (v_counter_factual[a] - v)
                cum_strategies[state_string][a] += my_reach * policies[epoch][state_string][a]
        return v

class AveragePolicy(policy.Policy):
    def __init__(self, game, player_ids, cum_strategy):
        super().__init__(game, player_ids)
        self.game = game
        self.cum_strategy = cum_strategy

    def action_probabilities(self, state, player_id=None):
        if player_id is None:
            player_id = state.current_player()
        legal_actions_mask = np.array(state.legal_actions_mask())
        tmp_policy = self.cum_strategy[state.information_state_string()]
        if tmp_policy.sum() > 0:
            tmp_policy = tmp_policy / tmp_policy.sum()
        else:
            tmp_policy = legal_actions_mask / legal_actions_mask.sum()
        return {i: tmp_policy[i] for i in range(self.game.num_distinct_actions())}


T = 100
for t in range(T):
    policies.append(defaultdict(lambda: np.ones(n_actions) / n_actions))
    for i in range(game.num_players()):
        ini_state = game.new_initial_state()
        cfr(ini_state, i, t, 1, 1)
        if (t + 1) % 1 == 0:
            ave_policy = AveragePolicy(game, list(range(game.num_players())), cum_strategies)
            payoffs = expected_game_score.policy_value(
                game.new_initial_state(),[ave_policy, ave_policy])
            exploitability.exploitability(game, ave_policy)

実験

Kuhn Poker

open_spielで実装されているcfrと比較してみます。

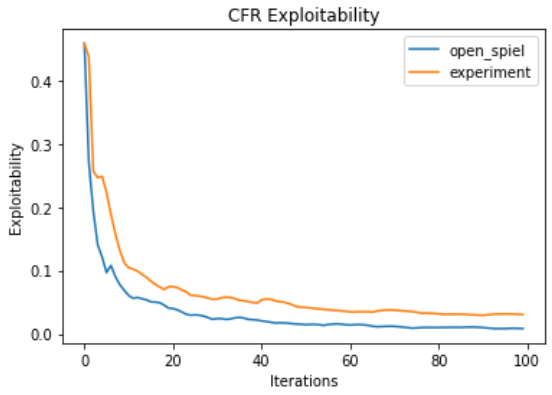
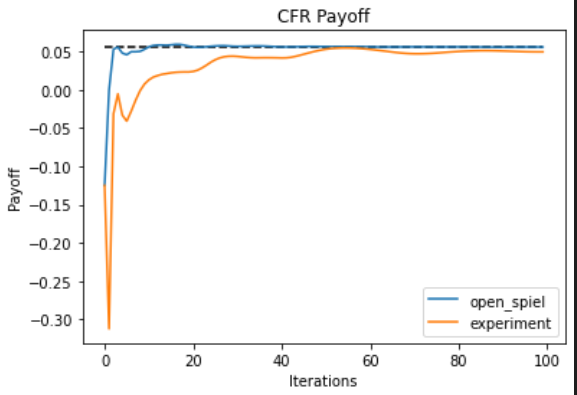
payoffの図の中の点線はKuhn Pokerのナッシュ均衡の期待利得です。
若干悪いですが、概ね同じような動きをしていそうです！

ちょっとした考察

さて、なぜopen_spielの実験結果と乖離があるのでしょうか？
答えとしては、regeret_matchingで更新するポリシーの更新タイミングが影響を与えています。
今回の実装ではcfr関数の中で更新していますが、open_spielでは（今回のものに合わせて記載すると）cfr関数の外で更新しています。
今回実装した上記のコードもcfr関数の外で更新するようにすればopen_spielと同じような性能になることは確認済みです！
ここまで読んでくださった方ならできると思いますのでぜひ上記試してみてください！
できたらコメントしていただけますと幸いです！

また一回のiterationで全プレイヤーを更新するか否かも性能に与える影響が大きいようです。
open_spielでは引数でコントロールできます。
検証もしやすそうです！

報酬が歪なジャンケンゲーム

open_spielでもmatrix_rpsとして提供されていますが、せっかくなのでちょっと変わったジャンケンを作ってみたいと思います。

open_spielで動くゲームの作成方法(python)

open_spielが提供している方法としては2つあります。

• efgファイルの形式で全ての状態を記載
  • 参考になるefgファイル
• pyspiel.Gameを継承して作成
  • 公式の説明

ジャンケンは状態数も少ないので一つ目の方法で作成します。

import pyspiel


BIASED_RPS = """
EFG 2 R "Biased RPS" { "Player1" "Player2" }
p "" 1 1 "" { "R" "P" "S" } 0
    p "" 2 1 "" { "R" "P" "S" } 0
        t "RR" 4 "Outcome RR" { 0.0 0.0 }
        t "RP" 5 "Outcome RP" { -1.0 1.0 }
        t "RS" 6 "Outcome RS" { 3.0 -3.0 }
    p "" 2 1 "" { "R" "P" "S" } 0
        t "PR" 7 "Outcome PR" { 1.0 -1.0 }
        t "PP" 8 "Outcome PP" { 0.0 0.0 }
        t "PS" 9 "Outcome PS" { -1.0 1.0 }
    p "" 2 1 "" { "R" "P" "S" } 0
        t "SR" 10 "Outcome SR" { -3.0 3.0 }
        t "SP" 11 "Outcome SP" { 1.0 -1.0 }
        t "SS" 12 "Outcome SS" { 0.0 0.0 }
"""
game = pyspiel.load_efg_game(BIASED_RPS)

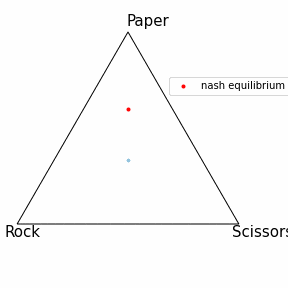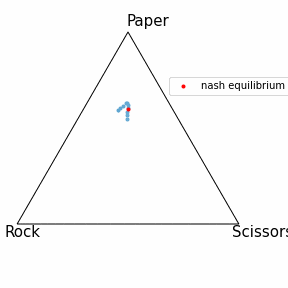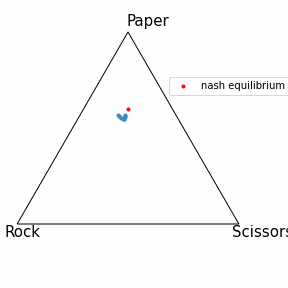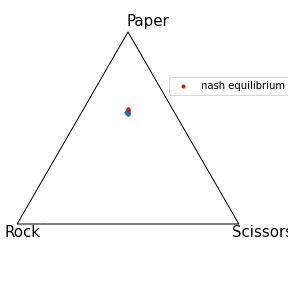
上記を使用した結果が下記になります。
記事上部に動いているものを記載したのでこちらでは静止画にしました。

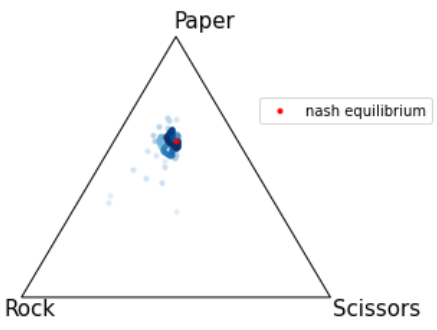
青点はCFRで学習した戦略を表しており、Iterationが進むほど色が濃くなっています。

結果としてしっかりと均衡点に近づいているように見えます！

まとめ

• ばかなおうじさんの記事を参考にCFRの実装を少しづつ進めました！
• kuhn_pokerでの実験で実装の結果実装は大丈夫そう！
• 報酬が歪なジャンケンでの実験の結果視覚的にも均衡に近づいていそう！

以上ありがとうございました！