はじめに
ボードゲームやカードゲームにおけるAIといえば囲碁やチェスなどの完全情報ゲームにおける成功が印象的ですが,ポーカーを中心とした不完全情報ゲームも着々と攻略されてきています.
不完全情報ゲームではナッシュ均衡戦略を最適戦略として求めるというアプローチがしばしば取られます.実際,2人プレイヤのポーカーでプロに匹敵する強さを見せたLibratus[1]でもナッシュ均衡戦略を求めることが行われています.このときにナッシュ均衡戦略を求めるためにしばしば用いられるのがCounterfactual Regret Minimization (CFR)[2]と呼ばれるアルゴリズムであり,Libratusや6人プレイヤのポーカーAIであるPluribus[3]もCFRを基礎としたアルゴリズムによって戦略を計算しています.
私が以前に書いた記事では,花札「こいこい」にCFRアルゴリズムを適用した実例について紹介しました.今回は,CFRのアルゴリズムについての解説と,そのアルゴリズムの実装方法についての紹介を行います.
Notation
ナッシュ均衡についての定義やCFRで出てくる数式の定義を行うために,いくつかの用語を定義します.
まず,有限の展開型不完全情報ゲームは以下の要素から構成されます.
- $N=\{1,\cdots,n\}$:$n$人のプレイヤの集合.
- $h$:ゲーム中の意思決定点(ノード).そこに至るまでのプレイヤの行動の履歴によって定義される.
- $H$:全ノードの集合.
- $Z(\subset H)$:それ以上行動を取ることができない終端ノードの集合.
- $A(h)=\{a ~|~ ha\in H\}$:ノード$h$で取ることが可能な行動の集合.
- $P(h)\in N\cup\{c\}$:ノード$h$で行動を取るプレイヤ.$P(h)=c$の場合,チャンスプレイヤが確率$\sigma_c(h,a)$で行動$a$を選択する.
- $u_i:Z\to \mathbb{R}$:プレイヤ$i\in N$の利得関数.二人零和ゲームの場合,すべての$z\in Z$について$u_1(z)=-u_2(z)$が成り立つ.
- $\mathcal I_i$:プレイヤ$i$の情報分割,すなわち,$H_i=\{h\in H ~|~ P(h) = i\}$の分割.
- $I\in \mathcal I_i$:情報集合,すなわち,プレイヤ$i$に属するノードの部分集合.$h,h^{\prime} \in I$であるとき,これらのノードはプレイヤ$i$からは区別できない.
また,戦略やノードへの到達確率を以下のように定義します.
- $\sigma(I)$:プレイヤが従う戦略.$A(I)$上の確率分布として定義される.ただし,$A(I)$は情報集合$I$で取ることが可能な行動の集合.
- $\sigma_i$:プレイヤ$i$の戦略,すなわち,各情報集合$I\in \mathcal I_i$から$A(I)$上の確率分布への関数.
- $\Sigma_i$:プレイヤ$i$の戦略の集合.
- $\pi^{\sigma}(h)$:全てのプレイヤが戦略$\sigma$に従って行動したとき,ノード$h$に到達する確率.
- $\pi^{\sigma}(h\to z)$:全てのプレイヤが戦略$\sigma$に従って行動したとき,ノード$h$に到達した状態からノード$z$へと到達する確率.
- $\pi_i^{\sigma}(h)$:プレイヤ$i$が戦略$\sigma$に従って行動し,それ以外のプレイヤが必ずノード$h$に向かうように行動するときに,ノード$h$に到達する確率.
- $\pi_{-i}^{\sigma}(h)$:プレイヤ$i$以外が戦略$\sigma$に従って行動し,プレイヤ$i$が必ずノード$h$に向かうように行動するときに,ノード$h$に到達する確率.
- $\pi^{\sigma}(I)=\sum_{h\in I}\pi^{\sigma}(h)$:戦略$\sigma$に従った際に,情報集合$I$に含まれるいずれかのノードに到達する確率.また,同様に,$\pi_i^{\sigma}(I)=\sum_{h\in I}\pi_i^{\sigma}(h)$,$\pi_{-i}^{\sigma}(I)=\sum_{h\in I}\pi_{-i}^{\sigma}(h)$とする.
- $u_i(\sigma)=\sum_{z\in Z}u_i(z)\pi^{\sigma}(z)$:戦略$\sigma$に従った際のプレイヤ$i$の期待利得.
ナッシュ均衡
定義
ナッシュ均衡は以下の式を満たす戦略の組み合わせ$\sigma^{\ast}=(\sigma_1^{\ast},\cdots,\sigma_n^{\ast})$として定義されます.
$$\forall i\in N, u_i(\sigma_i^{\ast}, \sigma_{-i}^{\ast}) \geq \max_{\sigma_i^{\prime}\in \Sigma_i} u_i(\sigma_i^{\prime}, \sigma_{-i}^{\ast})$$
また,$\epsilon$-ナッシュ均衡はナッシュ均衡の近似であり,以下のような式を満たす戦略の組み合わせ$\sigma^{\ast}=(\sigma_1^{\ast},\cdots,\sigma_n^{\ast})$として定義されます.
$$\forall i\in N, u_i(\sigma_i^{\ast}, \sigma_{-i}^{\ast}) + \epsilon \geq \max_{\sigma_i^{\prime}\in \Sigma_i} u_i(\sigma_i^{\prime}, \sigma_{-i}^{\ast})$$
なぜナッシュ均衡戦略に従うことが良いのか??
二人零和不完全情報ゲームではナッシュ均衡戦略を最適戦略として求めることがしばしば行われますが,これはなぜでしょうか??一般的なシングルプレイヤー設定の強化学習で行われるように利得(報酬)を最大化するような戦略を求めることはできないのでしょうか??
これに関しての説明を行うために,まず最初に,自分以外のプレイヤ全員の戦略が何かしらの戦略に固定されていて学習時にも実際のプレイ時にもその戦略に従っているケースを考えます.強化学習的に考えると,このケースでは相手のプレイヤは強化学習環境の一部であるとみなすことができるため,自分の期待利得は自分の戦略のみに依存していると考えることができます.なので,このケースではその環境のもとで利得を最大化するような戦略を求めれば良い,ということになり,この目的関数は一般的な強化学習の目的関数である報酬の最大化と一致することになります.
しかし,実際のプレイでは相手は学習時と同じ戦略を取ってくるかどうかはわかりませんし,色々なプレイヤと対戦することを考えると,相手の単一の戦略に対してだけでなく様々な戦略に対して強そうな戦略というものを考えたほうが良さそうです.なので,単一の戦略に対して利得を最大化する戦略を求めるようなアプローチでは良い戦略は得られないかもしれない,ということになってしまいます.
そこで代わりに最適戦略として定義されるのが,ナッシュ均衡です.ナッシュ均衡は,上述した定義から,どのプレイヤも自分だけが戦略を変えることによって,期待利得を上げることができないような戦略の組合せであることがわかります.特に,二人零和ゲームの場合,ナッシュ均衡戦略に従うことで相手の戦略に関係なく自分の期待利得を$u_1(\sigma_1^{\ast}, \sigma_2^{\ast})$以上にすることができます.これは利得の損失を最小限に抑えられることを意味しており,さらにこれに加えて対称性があるゲームの場合1,相手のどんな戦略に対しても期待利得が0以上になるため,ナッシュ均衡戦略は期待利得的に考えると負けない戦略である,ということが言えます.
これまでの説明をまとめると,**ナッシュ均衡戦略は,二人零和不完全情報ゲームでは利得の損失を最小限に抑えられる(特にゲームに対称性がある場合は期待利得が0以上になる)**という性質を持ちます.したがって,ナッシュ均衡戦略は相手の様々な戦略に対して安定して強い戦略であると考えられるため,二人零和不完全情報ゲームではナッシュ均衡戦略を最適戦略として求めることがしばしば行われます.
Counterfactual Regret Minimization
CFRは,反復的に戦略を更新することでナッシュ均衡を近似的に求めるアルゴリズムです.CFRでは,「この行動を取ったほうが良かった」という後悔 (regret) を小さくするように戦略を更新します.
Counterfactual Regret
CFRにおいて戦略の更新に用いられるregretは以下のようにして定義されます.
まず,CFRの反復$t$におけるプレイヤの戦略を$\sigma^t$とします.また,情報集合$I$に含まれるいずれかのノードから到達することができる終端ノードの集合を$Z_I$とし,ある終端ノード$z\in Z_I$へと到達することができる$I$中のノードを$z[I]$と定義します.情報集合$I$におけるプレイヤ$i$のcounterfactual value $v_i^{\sigma^t}$を以下の式で定義します.
$$v_i^{\sigma^t}(I)=\sum_{z\in Z_I}\pi_{-i}^{\sigma^t}(z[I])\pi^{\sigma^t}(z[I]\to z)u_i(z)$$
この式は,情報集合$I$に到達したときのプレイヤ$i$の期待利得に,プレイヤ$i$が必ず$I$に向かうように行動したときに$I$に到達する確率を重み付けしたものとなっています.同様にして,$v_i^{\sigma^t}(I,a)$をプレイヤ$i$が情報集合$I$において必ず行動$a$を選択するように戦略$\sigma^t$を変更した場合のcounterfactual valueと定義します.
counterfactual value $v_i^{\sigma^t}(I), v_i^{\sigma^t}(I,a)$を用いて,反復$t$において情報集合$I$で行動$a$を取ることに対するinstantaneous regret $r_i^t(I,a)$は以下の式で定義されます.
$$r_i^t(I,a)=v_i^{\sigma^{t}}(I,a)-v_i^{\sigma^{t}}(I)$$
この式は「情報集合$I$で行動$a$を取るように戦略$\sigma^t$を更新したらどの程度期待利得が増えるのか,ということを定式化したregretとなっています.
最後に,反復$T$において情報集合$I$で行動$a$を取ることに対するcounterfactual regret $R_i^T(I,a)$は,それまでの反復$t~(=1,\cdots,T)$におけるinstantaneous regretを用いて以下の式で定義されます.
$$R_i^T(I,a)=\sum_{t=1}^T r^t(I,a)$$
counterfactual regretはこれまでの反復のregretの累積になっているという点がポイントです.これでCFRの戦略の更新に必要なcounterfactual regretの定義ができましたので,次は戦略の更新式の説明に移ります.
戦略の更新式
CFRでは各反復$T$で各情報集合$I$,行動$a$に対してcounterfactual regret $R_i^T(I,a)$を計算し,それをベースに次反復の戦略$\sigma_i^{T+1}(I,a)$2を計算します.
$$
\sigma_i^{T+1}(I,a)=
\begin{cases}
\frac{R_i^{T,+}(I,a)}{\sum_{a^{\prime}\in A(I)}R_i^{T,+}(I,a^{\prime})} & \sum_{a^{\prime}\in A(I)}R_i^{T,+}(I,a^{\prime}) > 0 \\
\frac{1}{|A(I)|} & \mathrm{otherwise}
\end{cases}
$$
ただし,$R_i^{T,+}(I,a)=\max(R_i^T(I,a),0)$とします.これは,counterfactual regretが正の値である行動に対して,その行動を取る確率をregretの比率で与えるという処理であると解釈することができます.
最終的な出力
CFRにおいて特に注意しなければいけないのが,CFRが最終的な戦略として出力するのは最終反復$T$における戦略$\sigma_i^T$ではなく,以下の式で定義される**平均戦略$\bar{\sigma}_i^T$**であるという点です.
$$\bar{\sigma}_i^T(I,a) = \frac{\sum_{t=1}^T\left(\pi_i^{\sigma^t}(I)\sigma_i^t(I,a)\right)}{\sum_{t=1}^T\pi_i^{\sigma^t}(I)}$$
これは,CFRにおいて平均戦略はナッシュ均衡へと収束が保証されている[3]からであり,逆に各反復の戦略はナッシュ均衡へと収束する保証はありません.ナッシュ均衡の近似解を求めるためにCFRを用いることがほとんどだと思いますので,そのようなときには平均戦略を最終的な出力とすることを忘れないようにしましょう.
なお,平均戦略がナッシュ均衡へと収束することは,各反復$T$における平均戦略が$2\epsilon$-ナッシュ均衡となることから導くことができます.ただし,$\epsilon$は$\epsilon\leq \Delta_{u,i} |\mathcal{I}_i| \sqrt{|A_i|}/\sqrt{T}$を満たします3.この証明はこの記事では省略し,またの機会に行いたいと思います.
実装
前章ではCFRにおける戦略の更新方法や最終的な出力について説明しましたが,ここではCFRのアルゴリズムの実装について記述したいと思います.
CFRでは各反復ごとにすべての情報集合に対してinstantaneous regretを計算する必要がありますが,そのためにはすべての情報集合に対するcounterfactual value $v_i^{\sigma^{t}}(I),v_i^{\sigma^{t}}(I,a)$を計算する必要があります.その定義から,1つの情報集合$I$のcounterfactual valueの計算には情報集合に含まれる各ノードを根とした部分木を探索する必要があります.これを愚直にやろうとして各情報集合のcounterfactual valueをいちいち一から計算すると,同じノードを何度も何度も辿らないといけないことになってしまいます.これでは計算量がとんでもないことになってしまうので,ノードを辿る回数をできる限り少なくすることを考えます.
強化学習におけるvalue functionを知っている方にとっては当たり前なことに思われるかもしれませんが,counterfactual valueは以下のように式を変更することで再帰的な形へと書き直すことができます.
まず,ノード$h\in I$から到達することができる終端ノードの集合を$Z_I$とすると,counterfactual valueは以下のように変形できます.
$$v_i^{\sigma^t}(I)= \sum_{h\in I}\pi_{-i}^{\sigma^t}(h)\sum_{z\in Z_h}\pi^{\sigma^t}(h\to z)u_i(z)$$
ここで,$u_i^{\sigma^t}(h)=\sum_{z\in Z_h}\pi^{\sigma^t}(h\to z)u_i(z)$としvalueと呼ぶことにすると,$u_i^{\sigma^t}(h)$は以下のように再帰的に書くことができます.
\begin{align}
u_i^{\sigma^t}(h)&=\sum_{a\in A(h)}\sigma(h,a)\sum_{z\in Z_{ha}}\pi^{\sigma^t}(ha\to z)u_i(z)\\
&=\sum_{a\in A(h)}\sigma(h,a)u_i^{\sigma^t}(ha)
\end{align}
これはvalue $u_i^{\sigma^t}(h)$の計算には子ノードのvalueを計算すれば良いことを表しています.すべての終端ノードの利得が計算できればその親ノードのvalueが計算でき,それができればそのまた親ノードのvalueが計算でき,・・・,といった流れを繰り返すと,ゲーム木の根ノードを含めた全てのノードに対して再帰的にvalueを計算することができます.
この式を利用すると,ゲーム木の全ノードを一回ずつ辿るだけで,全ての情報集合に対するcounterfactual valueを計算することができます.以下の擬似コードはCFRのアルゴリズムであり,この擬似コードでも再帰的にvalueの計算を行っています.
関数CFRのパラメータは,行動履歴$h$,戦略を更新するプレイヤ$i$,現在の反復数$t$,ノード到達確率$\pi_{i}^{\sigma^t}(h)$,および$\pi_{-i}^{\sigma^t}(h)$です.変数$v_{\sigma}$はvalue $u_i^{\sigma^t}$に対応しています.
実装の仕方によっては各反復ですべてのプレイヤの戦略を同時に更新することもできますが,この擬似コードでは各プレイヤの戦略を交互に更新するようになっています.
実験
CFRのアルゴリズムがどの程度ナッシュ均衡に近い戦略を求められるかを調べるために,Kuhn Pokerと呼ばれるゲームにCFRを適用させる実験を行いました.実験に用いたコードはこちらに公開しています.
Kuhn Poker
Kuhn Pokerは非常に単純化されたポーカーであり,その単純さ故にゲーム理論を用いた完全な分析が可能な二人零和不完全情報ゲームです.
このゲームでは3枚(キング・クイーン・ジャックなどの3種類)のみのカードを用います.各プレイヤには3枚の中から1枚ずつカードが配られ,テキサスホールデムなどのようなポーカーと同様にベッドを行います.両方のプレイヤがベッドした場合,より高い数字のカードを持つプレイヤの勝利となり,利得$2$を得ます.両方のプレイヤがチェック(パス)した場合,より高い数字のカードを持つプレイヤの勝利となり,利得$1$を得ます.それ以外の場合(片方のプレイヤのみがベッドした場合),ベッドしたプレイヤの勝利となり,利得$1$を得ます.二人零和ゲームのため,負けたプレイヤの利得は勝利したプレイヤの利得に$-1$をかけた値となります.
Exploitability
CFRの平均戦略とナッシュ均衡との近さを確認するために,exploitabilityと呼ばれる指標を用います.二人零和ゲームにおいて,ある戦略$\sigma=(\sigma_1,\sigma_2)$のexploitability $\epsilon_{\sigma}$は以下の式で定義されます.
$$\epsilon_{\sigma}=\max_{\sigma_1^{\prime}} u_1(\sigma_1^{\prime}, \sigma_2) + \max_{\sigma_2^{\prime}} u_2(\sigma_1, \sigma_2^{\prime})$$
戦略$\sigma$がナッシュ均衡であるとき,このexploitabilityは$0$となります.逆にナッシュ均衡から離れた戦略となっている場合,$\max_{\sigma_1^{\prime}} u_1(\sigma_1^{\prime}, \sigma_2)$や$\max_{\sigma_2^{\prime}} u_2(\sigma_1, \sigma_2^{\prime})$は大きな値となるため,結果的にexploitabilityも$0$よりも大きな値となります.今回の場合はexploitabilityが$0$に近いほどナッシュ均衡に近い平均戦略が得られている,と考えてもらえれば良いと思います.
実験結果
各反復ごとの平均戦略のexploitabilityは以下のようになりました.
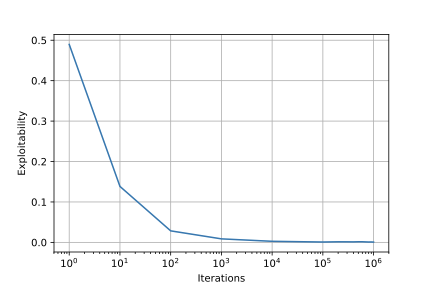
反復数が増加するにつれて平均戦略のexploitabilityが$0$に近づいていっており,平均戦略がナッシュ均衡へと近づいていっていることがわかります.
また,以下の図は,各反復$T$ごとの平均戦略$\bar{\sigma}^T=(\bar{\sigma}^T_1,\bar{\sigma}^T_2)$の期待利得$u_1(\bar{\sigma}^T)$と$u_2(\bar{\sigma}^T)$です.
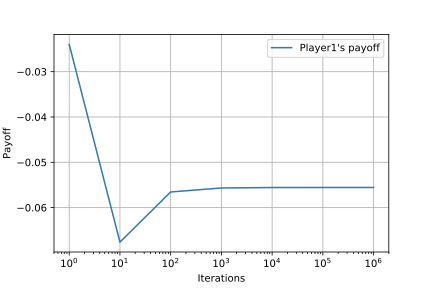
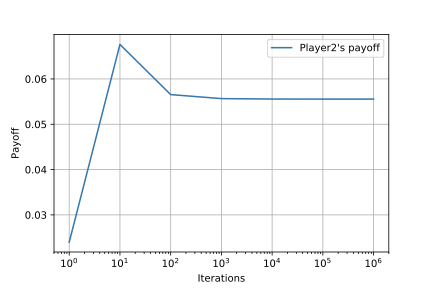
$u_1(\bar{\sigma}^T)$は$-\frac{1}{18}$へと,$u_2(\bar{\sigma}^T)$は$\frac{1}{18}$へと近づいていることがわかります.これらの値はKuhn Pokerのナッシュ均衡の期待利得と一致しており,この観点からも平均戦略がナッシュ均衡へと近づいていっていることがわかります.
おわりに
今回は,展開型不完全情報ゲームのナッシュ均衡計算アルゴリズムであるCFRについての解説を行いました.次回は平均戦略がナッシュ均衡へと収束することの証明の解説を行おうと思います.
今回の実験で用いた内容も含め,CFRの実装コードをこちらに公開しています.CFRだけでなく,モンテカルロ近似を用いることで反復ごとに辿るノードの数を減少させたMonte Carlo CFR[4]の実装も含まれていて,今後も色々とアップデートをしていく予定です.よかったらスターやプルリク,宣伝などお願いします m(_ _)m
参考文献
[1] Noam Brown and Tuomas Sandholm. Superhuman ai for heads-up no-limit poker: Libratus beats top professionals. Science, Vol. 359, No. 6374, pp. 418–424, 2018.
[2] Noam Brown and Tuomas Sandholm. Superhuman ai for multiplayer poker. Science, Vol. 365, No. 6456, pp. 885–890, 2019.
[3] Martin Zinkevich, Michael Johanson, Michael Bowling, and Carmelo Piccione. Regret minimization in games with incomplete information. In Advances in neural information processing systems, pp. 1729–1736, 2008.
[4] Marc Lanctot, Kevin Waugh, Martin Zinkevich, and Michael Bowling. Monte carlo sampling for regret minimization in extensive games. In Advances in neural information processing systems, pp. 1078–1086, 2009.
