概要
この記事では角速度センサと姿勢センサなどから姿勢クォータニオンを推定する伝統的な方法を紹介する.
姿勢クォータニオン概要
姿勢クォータニオンはロドリゲスの回転公式を基にする姿勢表現であり,回転の軸とその軸に対する回転方向を基に姿勢を決定する.
回転軸の方向ベクトルを$\boldsymbol{\lambda} \in \mathbb{R^3}$,回転角$\theta \in \mathbb{R}$とすると,姿勢クォータニオンは次のように定義される.時刻$t$は省略する.
\boldsymbol{q} =
\begin{bmatrix}
\boldsymbol{\lambda} \sin{\frac{\theta}{2}} \\
\cos{\frac{\theta}{2}}
\end{bmatrix}
:= \begin{bmatrix}
\boldsymbol{q}_v \\
q_4
\end{bmatrix}
:= \begin{bmatrix}
q_1 \\
q_2 \\
q_3 \\
q_4
\end{bmatrix}
明らかに,$\boldsymbol{q}$のユークリッドノルム($|| \boldsymbol{q} ||$)は1である.
同じ姿勢を示す姿勢クォータニオンは2つあり,ある姿勢クォータニオンの回転方向ベクトルと回転角の符号を反転すると,符号が異なる2つの姿勢クォータニオンで同じ姿勢を示すことになる.これでは都合が悪いので,常に全体に${\rm{sign}} \ q_4$をかけて$q_4$が正のものになるように修正する.
ここで,添え字$_v$はクォータニオンのベクトル部,$_4$はスカラー部を取り出す処理とする.
姿勢クォータニオンはクォータニオン $q_4+q_1i+q_2j+q_3k$ の各要素を無理やりベクトルとしてまとめたものであり,$\boldsymbol{q}$に対して通常の線形代数・ベクトル演算(行列積,内積,外積など)を使用することはできない.
ここで,クォータニオン積${\diamond}$を次のように定義する.
\boldsymbol{q} \diamond \boldsymbol{p} = \begin{bmatrix}
q_4 \boldsymbol{p}_v + \boldsymbol{q}_v p_4 + \boldsymbol{q}_v \times \boldsymbol{p}_v \\
q_4p_4 - \boldsymbol{q}_v \cdot \boldsymbol{p}_v
\end{bmatrix}
=
\begin{bmatrix}
q_4 \mathbb{I}_3 + [\boldsymbol{q}_v\times] & \boldsymbol{q}_v \\
-\boldsymbol{q}_v^{\rm{T}} & q_4
\end{bmatrix}
\begin{bmatrix}
\boldsymbol{p}_v \\
p_4
\end{bmatrix}
クォータニオン積に用いる記号はコンセンサスが得られていない感があり,記号不要としていたり$\otimes$を使っていたりする.これらは行列演算などでも用いるため紛らわしく,本記事では$\diamond$を用いることにする.
定義したクォータニオン積を用いて,姿勢クォータニオンの時間変化率を次のように表すことができる.
\frac{d}{dt} \boldsymbol{q} =
\frac{1}{2} \boldsymbol{q} \diamond \begin{bmatrix}
\boldsymbol{\omega} \\
0
\end{bmatrix}
姿勢クォータニオンも回転行列などと同様に,ベクトルを回転させるか座標系を回転させるかで共役のつけ方/かける順番が逆になる.
ベクトル部のクロス積項の符号を本来のクォータニオン積と逆にしたもので定義している文献もあり,この場合はクォータニオンをかける順番が逆になる.文献漁りの際はクォータニオン積の定義をよく確認することを推奨する(to 過去の自分).
共役クォータニオンは次のように定義される.
\boldsymbol{q}^* = \begin{bmatrix}
-\boldsymbol{q}_v \\
q_4
\end{bmatrix}
ユークリッドノルム$||\boldsymbol{q}||=a$となるとき,$\boldsymbol{q}\diamond\boldsymbol{q}^*
= \boldsymbol{q}^*\diamond\boldsymbol{q} = \left[0 \ 0 \ 0 \ a^2 \right]^{\rm{T}} \quad (=a^2+0i+0j+0k=a^2)$である.
(これを用いて,クォータニオンノルムは$\sqrt{\boldsymbol{q} \diamond \boldsymbol{q}^*}$で定義される)
ベクトル$\boldsymbol{r}$を$\boldsymbol{q}$によって回転すると次のようになる.
\begin{bmatrix} \boldsymbol{r}^\prime \\ 0 \end{bmatrix} = \boldsymbol{q} \diamond \begin{bmatrix} \boldsymbol{r} \\ 0 \end{bmatrix} \diamond \boldsymbol{q}^*
#Multiplicative Extended Kalman Filter (MEKF)
MEKFは姿勢クォータニオン推定によく用いられるフィルタである.以下にその方法を述べる。
モデリング
単純に姿勢クォータニオンの変化率と姿勢の角速度を状態変数にして拡張カルマンフィルタを組むのでもよいが,姿勢クォータニオンにはノルムの拘束条件がある.
これを利用し,次元を1つ小さくすることができる.
たかが次元1つではあるが,7次と6次ではカルマンフィルタ適用に要する計算リソースが大きく異なる.
伝統的な貧弱計算機では,多少の煩雑さを伴っても,下記のようなシステムモデル/観測モデルを利用するとよいだろう.
システムモデル
姿勢クォータニオンのベクトル部$q_v \in \mathbb{R^3}$,スカラー部$q_4 \in \mathbb{R}$として,姿勢クォータニオンを$q = \left[q_v^{\rm{T}} \ q_4 \right]^{\rm{T}}$,姿勢の推定誤差クォータニオンを$\delta q$とする.
姿勢の角速度を$\omega \in \mathbb{R^3}$,その推定誤差を$\delta \omega$とする.
各状態変数の推定量には$\hat{}$をつける.
姿勢,角速度を推定値周りで次のように分解する.
q = \hat{q} \diamond \delta q \\
\omega = \hat{\omega} + \delta \omega
姿勢クォータニオンの誤差がクォータニオン積を介して現れるため,線形カルマンフィルタを使うことができない.そのため,$\hat{q}$, $\hat{\omega}$周りで線形化したモデルを作成する.
$q$の時間変化率を求める.
まず,姿勢クォータニオンの性質から,次のようになる.
\begin{align}
\frac{d}{dt}q = \frac{1}{2} q \diamond \begin{bmatrix} \omega \\ 0 \end{bmatrix}
&= \frac{1}{2} \hat{q} \diamond \delta q \diamond \begin{bmatrix} \omega \\ 0 \end{bmatrix} \\
&= \frac{1}{2} \hat{q} \diamond \delta q \diamond \begin{bmatrix} \hat{\omega} +\delta\omega \\ 0 \end{bmatrix} \\
&= \frac{1}{2} \hat{q} \diamond \delta q \diamond \begin{bmatrix} \hat{\omega} \\ 0 \end{bmatrix}
+ \frac{1}{2} \hat{q} \diamond \delta q \diamond \begin{bmatrix} \delta\omega \\ 0 \end{bmatrix}
\end{align}
また,微分法のチェインルールから,次のようになる.
\begin{align}
\frac{d}{dt}q &= \frac{d}{dt} \left( \hat{q} \diamond \delta q \right) \\
&= \dot{\hat{q}} \diamond \delta q + \hat{q} \diamond \dot{\delta q} \\
&= \frac{1}{2} \hat{q} \diamond \begin{bmatrix} \hat{\omega} \\ 0 \end{bmatrix} \diamond \delta q + \hat{q} \diamond \dot{\delta q}
\quad \left(\because \dot{\hat{q}}=\frac{1}{2}\hat{q}\diamond\begin{bmatrix} \hat{\omega} \\ 0 \end{bmatrix} \right)
\end{align}
これらは一致するはずであるから,
\frac{1}{2} \hat{q} \diamond \delta q \diamond \begin{bmatrix} \hat{\omega} \\ 0 \end{bmatrix} + \frac{1}{2} \hat{q} \diamond \delta q \diamond \begin{bmatrix} \delta\omega \\ 0 \end{bmatrix}
= \frac{1}{2} \hat{q} \diamond \begin{bmatrix} \hat{\omega} \\ 0 \end{bmatrix} \diamond \delta q + \hat{q} \diamond \dot{\delta q}
となり,$\hat{q} \diamond$の中身を比較,あるいは左から$q^*$をかけることにより,次のようにできる.
\frac{1}{2} \delta q \diamond \begin{bmatrix} \hat{\omega} \\ 0 \end{bmatrix} + \frac{1}{2} \delta q \diamond \begin{bmatrix} \delta\omega \\ 0 \end{bmatrix}
= \frac{1}{2} \begin{bmatrix} \hat{\omega} \\ 0 \end{bmatrix} \diamond \delta q + \dot{\delta q} \\
=> \quad
\dot{\delta q} =
\frac{1}{2} \left( \delta q \diamond \begin{bmatrix} \hat{\omega} \\ 0 \end{bmatrix} - \begin{bmatrix} \hat{\omega} \\ 0 \end{bmatrix} \diamond \delta q + \delta q \diamond \begin{bmatrix} \delta\omega \\ 0 \end{bmatrix} \right)
ここで,$\delta q$ による姿勢の回転量は$\hat{q}$ に対して微小であるはずだから,$\left[0 \ 0 \ 0 \ 1\right]^{\rm{T}}$の近傍であるはずである.
そこで,微小回転角$\delta \theta \in \mathbb{R}^3$ として,次のように近似する.
\delta q \approx
\begin{bmatrix}
\frac{1}{2} \delta \theta \\
1
\end{bmatrix}
$\delta \theta$による近似とクォータニオン積の展開をしてまとめると次のようになる.
\begin{align}
\dot{\delta q}
&= \frac{1}{2} \left( \delta q \diamond \begin{bmatrix} \hat{\omega} \\ 0 \end{bmatrix} - \begin{bmatrix} \hat{\omega} \\ 0 \end{bmatrix} \diamond \delta q + \delta q \diamond \begin{bmatrix} \delta\omega \\ 0 \end{bmatrix} \right) \\
&=\frac{d}{dt} \begin{bmatrix} \frac{1}{2} \delta \theta \\ 1 \end{bmatrix}
= \frac{1}{2} \left( \begin{bmatrix}\frac{1}{2}\delta\theta\\1\end{bmatrix} \diamond \begin{bmatrix} \hat{\omega} \\ 0 \end{bmatrix} - \begin{bmatrix} \hat{\omega} \\ 0 \end{bmatrix} \diamond \begin{bmatrix}\frac{1}{2}\delta\theta\\1\end{bmatrix} + \begin{bmatrix}\frac{1}{2}\delta\theta\\1\end{bmatrix} \diamond \begin{bmatrix} \delta\omega \\ 0 \end{bmatrix} \right) \\
&=
\frac{1}{2} \left(
\begin{bmatrix}
\mathbb{I}_3 + \frac{1}{2} \left[ \delta \theta \times \right] & \frac{1}{2} \delta \theta \\
-\frac{1}{2}\delta \theta^{\rm{T}} & 1
\end{bmatrix}
\begin{bmatrix}
\hat{\omega} \\ 0
\end{bmatrix}
-
\begin{bmatrix}
\left[ \hat{\omega} \times \right] & \hat{\omega} \\
-\hat{\omega}^{\rm{T}} & 0
\end{bmatrix}
\begin{bmatrix}
\frac{1}{2} \delta \theta \\
1
\end{bmatrix}
+
\begin{bmatrix}
\mathbb{I}_3 + \frac{1}{2} \left[ \delta \theta \times \right] & \frac{1}{2} \delta \theta \\
-\frac{1}{2}\delta \theta^{\rm{T}} & 1
\end{bmatrix}
\begin{bmatrix}
\delta\omega \\ 0
\end{bmatrix} \right)\\
&=
\frac{1}{2} \left(
\begin{bmatrix}
\hat{\omega} + \frac{1}{2}\delta\theta\times\hat{\omega} - \frac{1}{2}\hat{\omega}\times\delta\theta - \hat{\omega} \\
-\frac{1}{2}\delta\theta^{\rm{T}} \hat{\omega} + \frac{1}{2}\hat{\omega}^{\rm{T}}\delta\theta
\end{bmatrix}
+
\begin{bmatrix}
\delta\omega + \frac{1}{2}\delta\theta\times\delta\omega \\
-\frac{1}{2}\delta\theta^{\rm{T}} \delta\omega
\end{bmatrix}
\right) \\
&=
\frac{1}{2} \left(
\begin{bmatrix}
- \hat{\omega}\times\delta\theta \\ 0
\end{bmatrix}
+
\begin{bmatrix}
\delta\omega + \frac{1}{2}\delta\theta\times\delta\omega \\
-\frac{1}{2}\delta\theta^{\rm{T}} \delta\omega
\end{bmatrix}
\right) \\
&\approx
\frac{1}{2} \left(
\begin{bmatrix}
- \hat{\omega}\times\delta\theta \\ 0
\end{bmatrix}
+
\begin{bmatrix}
\delta\omega \\ 0
\end{bmatrix}
\right) \quad \left(\because \ \delta q \delta\omega \approx 0 \right)
\\
=> \quad
&\dot{\delta \theta} =
\left[ - \hat{\omega} \times \right] \delta \theta + \mathbb{I}_3 \delta\omega \\
\end{align}
ここで,姿勢角速度のプロセスノイズ$n_{\omega}$は,$\delta\omega$と同じ項に入ると考えられるから,
\dot{\delta \theta} =
\left[ - \hat{\omega} \times \right] \delta \theta + \mathbb{I}_3 \delta\omega + \mathbb{I}_3 n_{\omega}
となる.同様に,$\dot{\omega} = 0 + n_{\dot{\omega}}$を考え,これらをまとめて,次のモデルを得る.
- 状態変数の予測モデル
\frac{d}{dt} \hat{q} = \frac{1}{2} \hat{q} \diamond \begin{bmatrix} \hat{\omega} \\ 0 \end{bmatrix} \\
\frac{d}{dt} \hat{\omega} = 0
- 拡張カルマンフィルタ構築用のモデル
\frac{d}{dt}
\begin{bmatrix}
\delta \theta \\
\delta \omega
\end{bmatrix}
=
\begin{bmatrix}
-\left[ \hat{\omega} \times \right] & \mathbb{I}_3 \\
0 & 0
\end{bmatrix}
\begin{bmatrix}
\delta \theta \\
\delta \omega
\end{bmatrix}
+
\begin{bmatrix}
\mathbb{I}_3 & 0 \\
0 & \mathbb{I}_3
\end{bmatrix}
\begin{bmatrix}
n_{\omega} \\
n_{\dot{\omega}}
\end{bmatrix}
このモデルを用いると,$q$の観測値から$q$,$\omega$ の推定値を得ることができる.
($\omega$が観測できなくても,$\omega$が推定できるということである)
$\hat{\omega}$と$\delta\omega$は,$\omega = \hat{\omega} + \delta\omega$と線形和で表されるにもかかわらず,モデルでの現れ方は線形的ではない.この意味としては,$\hat{\omega}$は計算機上で利用可能な値であり,$\delta\omega$はシステムが持っている利用できない値で,かつ他の微小値と積を取ったときに0とみなせるものである.
角速度が十分小さければ,$\hat{\omega}=0$ として扱ってもよいと考えられる.
なお,プロセスノイズ$n_{\omega}$を連続時間システムに突っ込むのはおかしい,というご指摘に関しては工学部マジックでOKとさせていただきたい.
(厳密には確率微分方程式で記述する必要がある)
ジャイロセンサを用いる場合
一般にはジャイロセンサがあるため,これをモデルに組み込みたい.
このとき,ジャイロセンサは一般にドリフトバイアスを持つため,これを推定する必要がある.
しかし,単純にドリフトバイアスをモデルに追加すると,次数が増大して計算コストも大きく増大する.
一般にジャイロセンサのノイズは角度センサのノイズより小さいため,ここでは角速度のノイズ取りを諦めてバイアス補正のみを行う.
ジャイロセンサのノイズが姿勢クォータニオンに与える影響は考慮できるため,姿勢の角速度より姿勢クォータニオンが重要という場合には十分有効である.
ジャイロセンサの観測データ$\omega_m$,ドリフトバイアスの真値$\omega_d$,推定値$\hat{\omega_d}$,推定誤差$\delta\omega_d$として,センサモデルを次のようにみなす.
\begin{align}
\omega_m
&= \omega + \omega _d + n_{\omega}\\
&:= \hat{\omega} + \hat{\omega}_d + \delta \omega_d + n_{\omega}
\end{align}
先のモデルを
\hat{\omega} = \omega_m - \hat{\omega}_d \\
\delta\omega=-\delta\omega_d-n_{\omega}
として差替えると次のモデルを得る.
- 状態量の予測モデル
\frac{d}{dt} \hat{q} = \frac{1}{2} \hat{q} \diamond \begin{bmatrix} \omega_m - \hat{\omega}_d \\ 0 \end{bmatrix} \\
\frac{d}{dt} \hat{\omega}_d = 0 \\
- 拡張カルマンフィルタ構築用のモデル
\frac{d}{dt}
\begin{bmatrix}
\delta \theta \\
\delta \omega_d
\end{bmatrix}
=
\begin{bmatrix}
-\left[ \left(\omega_m - \hat{\omega}_d \right) \times \right] & -\mathbb{I}_3 \\
0 & 0
\end{bmatrix}
\begin{bmatrix}
\delta \theta \\
\delta \omega_d
\end{bmatrix}
+
\begin{bmatrix}
-\mathbb{I}_3 & 0 \\
0 & \mathbb{I}_3
\end{bmatrix}
\begin{bmatrix}
n_{\omega} \\
n_{\dot{\omega}}
\end{bmatrix}
一般的に,このシステムモデルがMEKFと呼ばれているようである.
観測モデル
センサとしては,姿勢状態を直接得られるセンサ,あるいは,慣性系に対して固定されたベクトルの方向を検出できるセンサがあると仮定する.
ジャイロセンサは先のシステムモデルのモデル化で組み込んでいる.
ここでは,観測値と推定した観測値の差分$y_m - y(\hat{\delta \theta})$から,観測方程式を導出する.
一般論
$y = h(x)$ で表される非線形の観測方程式があるとき,これを推定値周りでテイラー展開すると,次のようになる.
y(x_m) \approx y(\hat{x}) + \left.\frac{\partial h(x)}{\partial x}\right|_{x=\hat{x}}(x_m-\hat{x})
これから,$y(x)$の観測値と推定値の差を求めると次式になる.
y(x_m) - y(\hat{x}) \approx \left.\frac{\partial h(x)}{\partial x}\right|_{x=\hat{x}}(x_m-\hat{x})
= \left.\frac{\partial h(x)}{\partial x}\right|_{x=\hat{x}} x_m - \left.\frac{\partial h(x)}{\partial x}\right|_{x=\hat{x}} \hat{x}
ここで,カルマンフィルタ設計のための線形化した観測方程式は,
y(x) \approx \left.\frac{\partial h(x)}{\partial x}\right|_{x=\hat{x}} x
とすればよい(テイラー展開の初項は無視できる).
実際のフィルタリング時には,テイラー展開をせずに (センサ観測値)$-y(\hat{x})$ を使えばよい.
一般論 (for MEKF)
$y(q) = h(q)$のとき,次のように書ける.
y(q) \approx \begin{bmatrix} \frac{\partial h(q)}{\partial q}\frac{\partial q}{\partial \delta\theta} & \frac{\partial h(q)}{\partial \delta\omega} \end{bmatrix}
\begin{bmatrix} \delta\theta \\ \delta\omega \end{bmatrix}
姿勢角を直接観測できる場合(スタートラッカーなど)
姿勢角が直接観測できる場合,$\hat{q}$周りで$\delta q$ を陽に表すことができる.
q = \hat{q} \diamond \delta q \\
=> \quad \delta q = \hat{q}^* \diamond q \\
=> \quad \delta \theta = 2(\hat{q}^* \diamond q)_v
観測した姿勢クォータニオンを$q_m$とすると,
q_m = \hat{q} \diamond \delta q_m \\
=> \delta \theta_m = 2(\hat{q}^* \diamond q_m)_v
となる.推定値$\hat{q}$では,
\hat{q} = \hat{q} \diamond \hat{\delta q}\\
=> \hat{\delta \theta} = 2(\hat{q}^* \diamond \hat{q})_v
= 2\left(\begin{bmatrix}0 \\ 0 \\ 0 \\ 1 \end{bmatrix}\right)_v = 0_3
となるため,$\delta \theta_m - \hat{\delta \theta} = \delta \theta_m$ である.
線形化した観測方程式としては,上記のように$\delta \theta$ を直接得られるため,
y =
\begin{bmatrix}
\mathbb{I}_3 & 0_{3,3}
\end{bmatrix}
\begin{bmatrix}
\delta \theta \\
\delta \omega
\end{bmatrix}
となる.
観測更新量は,カルマンゲイン$K$として,
\begin{bmatrix} \Delta\theta \\ \Delta\omega \end{bmatrix} = K \delta\theta _m
となる.
方向ベクトルを観測できる場合(重力,磁気,太陽方向など)
重力などの慣性空間に対して固定された方向ベクトルがある場合,直接$\delta \theta$を観測することができないが,方向ベクトルの観測値と推定した方向ベクトルとの差分を利用することができる.
そのため,固定ベクトルを方向余弦行列(DCM)で移す$q$の非線形関数を考え,これを線形化した観測方程式を用いることにする.
姿勢クォータニオン$q$から,DCMを$q$から求める関数を$A(q)$,固定された方向ベクトルを$v$として,次のように得られる.
\begin{align}
y(q) &= A(q)v \\
&= A\left(\hat{q} \diamond \delta q\right) v \\
&= A\left(\hat{q} \diamond \begin{bmatrix} \frac{1}{2} \delta \theta \\ 1 \end{bmatrix} \right) v \\
\\
y(q_m) - y(\hat{q}) &= \left. \frac{\partial}{\partial \delta \theta} \left\{ A\left(\hat{q} \diamond \begin{bmatrix} \frac{1}{2} \delta \theta \\ 1 \end{bmatrix} \right) v \right\} \right|_{\delta\theta=\hat{\delta\theta}=0 } \delta\theta _m
\end{align}
線形化した観測方程式は,
y(q) = \begin{bmatrix} \left. \frac{\partial}{\partial \delta \theta} \left\{ A\left(\hat{q} \diamond \begin{bmatrix} \frac{1}{2} \delta \theta \\ 1 \end{bmatrix} \right) v \right\} \right|_{\delta\theta=\hat{\delta\theta}=0 } & 0_{3,3} \end{bmatrix}
\begin{bmatrix} \delta \theta \\ \delta \omega \end{bmatrix}
となる(はず).
手計算で求めると絶対に間違うので,SymPyなどの数式処理ライブラリを使うか数値微分を使うと良い.
なお,近年のこの用途ではMadgwick Filterが流行っているようである.
推定量の更新
ここまでで,システムモデルと観測モデルを導けたので,後はセオリー通りにカルマンフィルタを適用すればよい.
ここで,上記のモデルは$\hat{q}$と$\hat{\omega}$あるいは$\hat{\omega _d}$周りで線形化しているため,これらを真値の近傍になるように常に更新する必要がある.
カルマンゲイン$K$による更新量$\Delta x=K(y_m-\hat{y})$とすると,これらの成分を2つ分けて,
\begin{bmatrix} \Delta \theta \\ \Delta \omega \end{bmatrix} = K(y_m-\hat{y})
状態量は真値と推定値の差で表されるが,真値の方は動かせないので推定値を更新する.
角速度の更新は線形的にできる.
\hat{\omega}^{\rm{new}} = \hat{\omega} + \Delta \omega
\quad \rm{or} \quad
\hat{\omega _d}^{new} = \hat{\omega}_d + \Delta \omega
姿勢クォータニオン$\hat{q}$の更新には2つの方法があるが,中身は一致する.
$\omega dt = \Delta \theta$ とみなし,微小時間での回転を足すのが1つの方法である.
\begin{align}
\hat{q}^{\rm{new}} &= \hat{q} + \frac{dq}{dt} dt \\
&= \hat{q} + \frac{1}{2} \hat{q} \diamond \begin{bmatrix} \omega \\ 0 \end{bmatrix} dt
= \hat{q} + \frac{1}{2} \hat{q} \diamond \begin{bmatrix} \omega dt \\ 0 \end{bmatrix} \\
&= \hat{q} + \frac{1}{2} \hat{q} \diamond \begin{bmatrix} \Delta \theta \\ 0 \end{bmatrix} \\
&= \begin{bmatrix}
\hat{q}_v + \frac{1}{2}\hat{q}_4 \Delta \theta - \frac{1}{2} \hat{q}_v \times \Delta \theta \\
\hat{q}_4 - \frac{1}{2} \hat{q}_v^{\rm{T}} \Delta \theta
\end{bmatrix}
\end{align}
これは,
\hat{q}^{\rm{new}} = \hat{q} \diamond \begin{bmatrix} \frac{1}{2} \Delta \theta \\ 1 \end{bmatrix}
としたときと中身が一致している.どちらを用いてもよい.
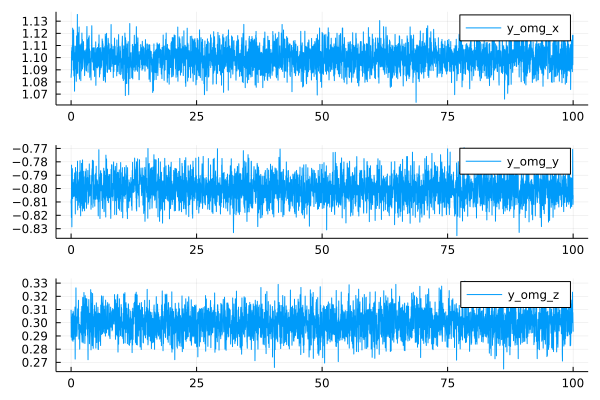
シミュレーション
初期値 $q = \begin{bmatrix} 0 & 0 & 0 & 1 \end{bmatrix}^{\rm{T}} $
角速度 $\omega (t) = \begin{bmatrix} 1.0 & -1.0 & 0 \end{bmatrix}^{\rm{T}} \ \rm{deg/s = const.}$
観測ノイズ $(\theta)$ $\quad 0.3 \ \rm{deg} \quad (1\sigma) $
観測ノイズ $(\omega)$ $\quad 0.01 \ \rm{deg/s} \quad (1\sigma) $
ドリフトバイアス $\omega _d = \begin{bmatrix} 0.1 & 0.2 & 0.3 \end{bmatrix}^{\rm{T}} \ \rm{deg/s} $
観測周期 $32 \rm{Hz}$
文献
[1] Lefferts, Eugene & Markley, Landis & Shuster, Malcolm. (1982). Kalman Filtering for Spacecraft Attitude Estimation. Journal of Guidance, Control, and Dynamics. 5. 10.2514/3.56190.
https://www.researchgate.net/publication/4693629_Kalman_Filtering_for_Spacecraft_Attitude_Estimation
[2] Queen, Steven Z., NASA, A KALMAN FILTER FOR MASS PROPERTY AND THRUST IDENTIFICATION OF THE SPIN-STABILIZED MAGNETOSPHERIC MULTISCALE FORMATION, International Symposium on Space Flight Dynamics, 2015
https://ntrs.nasa.gov/citations/20150019913
[3] Qin, F.; Chang, L.; Jiang, S.; Zha, F. A Sequential Multiplicative Extended Kalman Filter for Attitude Estimation Using Vector Observations. Sensors 2018, 18, 1414. https://doi.org/10.3390/s18051414
備考
何か間違ってたらコメントください.
スパゲッティソース
# Julia 1.7.0
using Plots; gr()
using LinearAlgebra; using Statistics
using SymPy
eye(n::T) where T = Matrix{T}(I,n,n)
eye(T::DataType, n::Int64) = Matrix{T}(Matrix{Int64}(I,n,n))
# ダイナミクスとか
dxdt_Ax(A::Matrix{Float64}, x::Vector{Float64}) = A * x
# 4次ルンゲ・クッタ
function solve_RK4_Aomgt_x(T::StepRangeLen{Float64,Base.TwicePrecision{Float64},Base.TwicePrecision{Float64}},x0::Vector{Float64})
dt = T[2] - T[1]
X = [zeros(length(x0)) for i = 1: length(T)]
X[1] = copy(x0)
x = copy(x0)
for i = 1 : length(T) - 1
t = T[i]
k1 = dxdt_Ax(A(omg(t)), x)
k2 = dxdt_Ax(A(omg(t+0.5dt)), x+k1*0.5dt)
k3 = dxdt_Ax(A(omg(t+0.5dt)), x+k2*0.5dt)
k4 = dxdt_Ax(A(omg(t+dt)), x+k3*dt)
x = x + (k1 + 2k2 + 2k3 + k4) * dt/6
x = normalize(x) *sign(x[4])
X[i+1][:] = x
end
return X
end
# クォータニオンの時間変化率計算
#dqdt = 1/2*q_cross(q, [omega;0.]) = A(omega) * q
A(o::Vector{T}) where T = [0 o[3] -o[2] o[1];
-o[3] 0 o[1] o[2];
o[2] -o[1] 0 o[3];
-o[1] -o[2] -o[3] 0] * (1/2)
# dqdt = 1/2 * Xi(q) * omega
Xi(q::Vector{T}) where T = [q[4]*eye(3) + cross_operator(q[1:3]);
-transpose(q[1:3])]
# 外積オペレータ
cross_operator(r::Vector{T}) where T = [0 -r[3] r[2];
r[3] 0 -r[1];
-r[2] r[1] 0]
# クォータニオン積
q_cross(qv::Vector{Sym},q4::Sym,pv::Vector{Sym},p4::Sym) = ([q4*pv + qv*p4 + cross(qv,pv); q4*p4 - qv'*pv])
function q_cross(qv::Vector{T},q4::T,pv::Vector{T},p4::T) where T <: Number
qw = q4*p4 - qv'*pv
return ([q4*pv + qv*p4 + cross(qv,pv); qw]) * sign(qw)
end
q_cross(q::Vector{T},p::Vector{T}) where T = q_cross(q[1:3], q[4], p[1:3], p[4])
# 共役クォータニオン
qinv(q::Vector{T}) where T <: Number = [-q[1]; -q[2]; -q[3]; q[4]] * sign(q[4])
qinv(q::Vector{Sym}) = [-q[1]; -q[2]; -q[3]; q[4]]
### シミュレーション設定
# シミュレーション用の時間設定 (1024Hz)
dt_sim = 1 / 2^10
T_sim = 0.0 : dt_sim : 100.0
# 最終的なサンプリングデータの時間設定 (32Hz)
dt = 1 / 2^5
T = T_sim[1] : T_sim[1+round(Int,dt/dt_sim)]-T_sim[1] : T_sim[end]
# 初期値設定
x0 = normalize([0.; 0.; 0.; 1.])
# 角速度の真値
omg(t::T) where T = deg2rad.([1; -1; 0])
# ノイズ設定
sigma_theta = deg2rad(0.3)
sigma_omg = deg2rad(0.01)
drift_omg = deg2rad.([0.1; 0.2; 0.3])
macro cal_dat()
esc(:(
begin
# サンプル曲線(真値)を作成 (1024 Hz)
X = solve_RK4_Aomgt_x(T_sim, x0)
# 結果を要素ごとの変数に分解 (32Hz)
q = X[1:round(Int,dt/dt_sim):end]
q1 = [qq[1] for qq in q]
q2 = [qq[2] for qq in q]
q3 = [qq[3] for qq in q]
q4 = [qq[4] for qq in q]
omg_xyz = omg.(T)
omg_x = [o[1] for o in omg_xyz]
omg_y = [o[2] for o in omg_xyz]
omg_z = [o[3] for o in omg_xyz]
# ノイズを印加
# クォータニオンの観測データ系列
sigma_q = sigma_theta /2
y_q = [normalize([q1[i]; q2[i]; q3[i]; q4[i]] + sigma_q * randn(4)) for i = 1:length(T)]
y_q1 = [yq[1] for yq in y_q]
y_q2 = [yq[2] for yq in y_q]
y_q3 = [yq[3] for yq in y_q]
y_q4 = [yq[4] for yq in y_q]
# 角速度の観測データ系列
y_omg = [omg_xyz[i] + drift_omg + sigma_omg*randn(3) for i = 1:length(T)]
y_omg_x = [yo[1] for yo in y_omg]
y_omg_y = [yo[2] for yo in y_omg]
y_omg_z = [yo[3] for yo in y_omg]
# プロット
plot_y_omg_x = plot(T, rad2deg.(y_omg_x), label="y_omg_x")
plot_y_omg_y = plot(T, rad2deg.(y_omg_y), label="y_omg_y")
plot_y_omg_z = plot(T, rad2deg.(y_omg_z), label="y_omg_z")
plot_y_omg = plot(plot_y_omg_x, plot_y_omg_y, plot_y_omg_z, layout=(3,1))
plot_y_q1 = plot(T, y_q1, label="y_q1")
plot_y_q2 = plot(T, y_q2, label="y_q2")
plot_y_q3 = plot(T, y_q3, label="y_q3")
plot_y_q4 = plot(T, y_q4, label="y_q4")
plot_y_q = plot(plot_y_q1, plot_y_q2, plot_y_q3, plot_y_q4, layout=(4,1))
end
))
end
### プロセスノイズの状態遷移積分
function cal_Qk(A::Matrix{Float64},G::Matrix{Float64},Q::Matrix{Float64},dt::Float64)
GQG = G * Q * G'
return (eye(size(A,1))) * GQG * (eye(size(A,1)))' * dt +
(eye(size(A,1))) * GQG * (A)' * (1/2*dt^2) +
(eye(size(A,1))) * GQG * (1/2*A^2)' * (1/3*dt^3) +
(A) * GQG * (eye(size(A,1)))' * (1/2*dt^2) +
(A) * GQG * (A)' * (1/3*dt^3) +
(A) * GQG * (1/2*A^2)' * (1/4*dt^4) +
(1/2*A^2) * GQG * (eye(size(A,1)))' * (1/3*dt^3) +
(1/2*A^2) * GQG * (A)' * (1/4*dt^4) +
(1/2*A^2) * GQG * (1/2*A^2)' * (1/5*dt^5)
end
### カルマンフィルタ
function MEKF(T::StepRangeLen{Float64, Base.TwicePrecision{Float64}, Base.TwicePrecision{Float64}},
q_hat_0::Vector{Float64}, drift_hat_0::Vector{Float64}, P_0::Matrix{Float64},
Q::Matrix{Float64}, R::Matrix{Float64},
y_q_dat::Vector{Vector{Float64}}, y_omg_dat::Vector{Vector{Float64}})
dt = T[2] - T[1]
q_hat = copy(q_hat_0)
drift_hat = copy(drift_hat_0)
P = copy(P_0)
Q_HAT = [zeros(4) for i in T]
DRIFT_HAT = [zeros(3) for i in T]
K_DAT = [zeros(6,3) for i in T]
P_DAT = [zeros(6,6) for i in T]
Qk_DAT = [zeros(6,6) for i in T]
P_DAT[1][:,:] = P_0
Q_HAT[1][:,:] = q_hat_0
DRIFT_HAT[1][:] = drift_hat_0
G = [eye(3) zeros(3,3); zeros(3,3) eye(3)];
H = [eye(3) zeros(3,3)]
for i = 2 : length(T)
omg_hat = y_omg_dat[i] - drift_hat
y_q = y_q_dat[i]
# 予測
q_hat_predict = exp(A(omg_hat)*dt) * q_hat
Ad = [-cross_operator(omg_hat) -eye(3);
zeros(3,3) zeros(3,3)]
F = exp(Ad * dt)
Qk = cal_Qk(Ad, G, Q, dt)
P_predict = F * P * F' + Qk
# カルマンゲイン計算
K = P_predict * H' * inv(H * P_predict * H' + R)
# 観測更新
P = (eye(6) - K * H) * P_predict * (eye(6) - K * H)' + K * R * K'
dq = normalize(q_cross(qinv(q_hat_predict), y_q))
dx = K * 2*dq[1:3] / dq[4]
# 推定量更新
q_hat = q_hat_predict + 1/2*Xi(q_hat_predict)*dx[1:3]
q_hat = normalize(q_hat) * sign(q_hat[4])
drift_hat += dx[4:6]
# データ保存
Q_HAT[i][:] = q_hat
DRIFT_HAT[i][:] = drift_hat
K_DAT[i][:,:] = K
P_DAT[i][:,:] = P
Qk_DAT[i][:,:] = Qk
end
return Q_HAT, DRIFT_HAT, K_DAT, P_DAT, Qk_DAT
end
macro cal_mekf()
esc(:(
begin
# カルマンフィルタ用 ノイズ共分散設定
Q = [sigma_omg^2*eye(3) zeros(3,3) ;
zeros(3,3) sigma_omg^2*eye(3)] / dt
R = sigma_theta^2 * eye(3)
# 初期値設定
q_hat_0 = copy(y_q[1])
drift_hat_0 = zeros(3)
P_0 = [sigma_theta^2*eye(3) zeros(3,3);
zeros(3,3) (maximum(drift_omg))^2 * eye(3)]
# MEKF実行
Q_HAT, DRIFT_HAT, K_DAT, P_DAT, Qk_DAT = MEKF(T, q_hat_0, drift_hat_0, P_0, Q, R, y_q, y_omg)
q1_hat = [qh[1] for qh in Q_HAT]
q2_hat = [qh[2] for qh in Q_HAT]
q3_hat = [qh[3] for qh in Q_HAT]
q4_hat = [qh[4] for qh in Q_HAT]
drift_hat_x = [rad2deg(bh[1]) for bh in DRIFT_HAT]
drift_hat_y = [rad2deg(bh[2]) for bh in DRIFT_HAT]
drift_hat_z = [rad2deg(bh[3]) for bh in DRIFT_HAT]
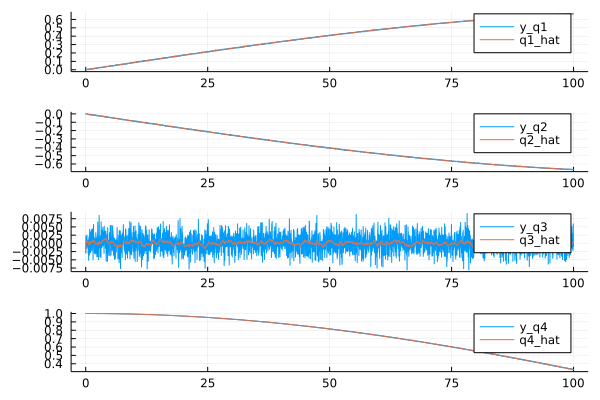
plot_q1 = plot(plot_y_q1, T, q1_hat,labels="q1_hat")
plot_q2 = plot(plot_y_q2, T, q2_hat,labels="q2_hat")
plot_q3 = plot(plot_y_q3, T, q3_hat,labels="q3_hat")
plot_q4 = plot(plot_y_q4, T, q4_hat,labels="q4_hat")
plot_q_hat = plot(plot_q1, plot_q2, plot_q3, plot_q4, layout = (4,1))
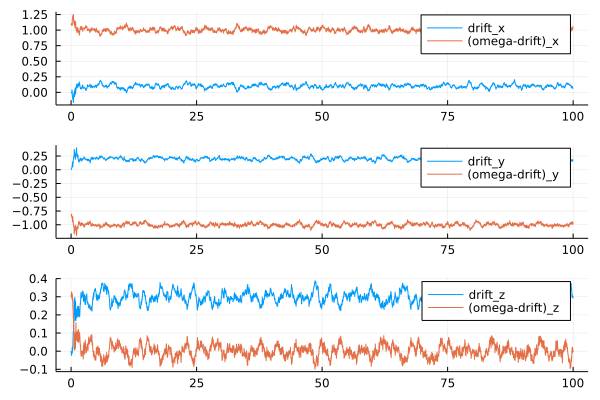
plot_drift_x = plot(T, [drift_hat_x rad2deg.(y_omg_x)-drift_hat_x], labels=["drift_x" "(omega-drift)_x"])
plot_drift_y = plot(T, [drift_hat_y rad2deg.(y_omg_y)-drift_hat_y], labels=["drift_y" "(omega-drift)_y"])
plot_drift_z = plot(T, [drift_hat_z rad2deg.(y_omg_z)-drift_hat_z], labels=["drift_z" "(omega-drift)_z"])
plot_drift = plot(plot_drift_x, plot_drift_y, plot_drift_z, layout=(3,1))
end
))
end
@cal_dat
@cal_mekf