つくってまなぶ★DES☆

この記事は信州大学kstmアドベントカレンダー2019の三日目の記事です。
去年と同様に 人不足のため わたくし @arsley の1/2回目の記事となります。よろしくお願いします。

導入

本記事では私がゼミにて勉強した DES (Data Encryption Standard) とかいう「暗号化方式の1手法として聞いたことはあるけど、どういうものか知らない」という技術について、 得た知識をすぐに他者に伝えマウントをとってしまう若き頃のような気持ちで 実装例を挙げながら説明します。
これを機に暗号分野にホーーーーンの少しでも興味を持っていただければ幸いです

TL;DWR

too long don't wanna read
完成品はこちら(3分間クッキング)(Ruby実装)(雑README)

「手っ取り早くどういう挙動をするものなのか知りたい」という方はご参照ください。

DES (Data Encryption Standard)

DES (Data Encryption Standard) は共通鍵暗号方式のブロック暗号の一つです。
64ビットをブロック長、鍵も同じく64ビットで与え一連の暗号化処理により暗号文を得ます。
ただし、鍵については64ビットのうち8ビットは誤り訂正ビット（パリティビット）として扱うため、実際の鍵長は56ビットとなります。
また、暗号化に用いた 共通の 鍵を用いて暗号文の復号を行うことが可能です。

共通鍵暗号は字面でわかると思うので、ブロック暗号について少しだけ補足します。

ブロック暗号

ブロック暗号とは、その名の通りデータを固定長の ブロック という単位に区切り、ブロックごとに暗号化を行う方式のことを指します。
共通鍵暗号におけるもう一つの暗号化方式はストリーム暗号と呼ばれるもので、1ビットもしくは1バイト単位で逐次暗号化していく方式のことを指します。

一般的にブロック暗号は、ラウンド関数と呼ばれる処理を繰り返し適用し暗号文を得る構造となっており、これをFeistel構造と言います。
DESの開発者であるHorst Feistelに由来するそうです¹。
また、暗号には平文→暗号文といった暗号化のほかに、暗号文→平文といった復号が可能である必要がある（復号可能性）のですが、このFeistel構造は逆変換が自身と同じ形になることから復号可能性を保証できるそうです。不思議ですね
もちろんDESもこのFeistel構造により実装されています。

ちょっとわかりにくいので「逆変換が自身と同じ形になる」ということを線形代数の一次変換でお話をすると、たとえば点 $(x,y)$ から $(x^\prime, y^\prime)$ への一次変換を

A =
\left(
\begin{matrix}
  1 & 0 \\
  0 & 1
\end{matrix}
\right)

\left(
\begin{matrix}
  x^\prime \\
  y^\prime
\end{matrix}
\right)
=
A
\left(
\begin{matrix}
  x \\
  y
\end{matrix}
\right)

で与えると、これの逆変換すなわち$A^{-1}$も同じであり、これが「逆変換が自身と同じ形になる」ということの意です（多分）。

DESのDEA (Data Encryption Algorithm)

以降、転置表などのデータはこちらのサイトのものを利用させていただいています。

DESにおいて暗号文を得るまでのプロセスをDEA（Data Encryption Algorithm）と呼ぶこともあるそうです初耳でした。

上述したように、DESはラウンド関数を繰り返し適用するFeistel構造により構成されます。
64ビット長のデータをブロックとして扱い、同じく64ビットを鍵として扱います（実際に使う鍵長は56ビット）。

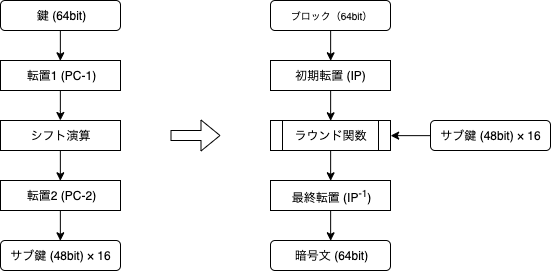
DESは大きく分けて次の手順で暗号化を行います。

1. 元々の鍵64ビットから転置・シフト演算を用いて16個のサブ鍵を取得
2. ブロックの初期データに対し初期転置を適用
3. (2)にて得られたデータに対しサブ鍵と共にラウンド関数へ適用

• これを16回繰り返す

1. (3)にて得られたデータに対して最終転置を適用、これを暗号文とする

図にするとこんな感じです。

転置

中身を明らかにする前に、転置という操作について説明します。
例えば8文字の文字列 abcdefgh に対して次のような数列

8 7 6 5 4 3 2 1

が与えられた時、これは元の文字列を hgfedcba に変換することを意味します。
具体的にいうと、「元の文字列における8番目を1文字目に、元の文字列における7番目を2文字目に、元の文字列における6番目を3文字目に...置き直す（転置する）」という操作を行わせることを意味します。

サブ鍵生成

まずサブ鍵生成について説明します。
今回鍵としては文字列 kkkeeyyy の2進表記 $0110101101101011011010110110010101100101011110010111100101111001$ を利用します。

以下は文字列→二進表記変換の例です²。

key_bin = key.bytes.map { |k| k.to_s(2).rjust(8, '0') }.join

転置1 PC-1

まずはじめに最初の転置 PC-1 を行います。
この転置PC-1は次の数列により表されます³。

PC-1

57 49 41 33 25 17 9 1 58 50 42 34 26 18 10 2 59 51 43 35 27 19 11 3 60 52 44 36 63 55 47 39 31 23 15 7 62 54 46 38 30 22 14 6 61 53 45 37 29 21 13 5 28 20 12 4

転置を行い得られたビット列は $00000000111111111111111111100000011100011000111001110000$ となります（めっちゃ整っててびっくり）。
この転置から使われているのは 8,16,24,32,40,48,56,64 を除く56ビットであり、鍵長が与えたデータよりも短いことがわかるかと思います。

転置処理には map を用いるのが楽かなと思います⁴。

PC1.map { |index| key_bin.chars[index] }

シフト演算

シフト演算はその名の通り、与えられたビット列を左方向へシフトさせるものです。
ここで用いるシフト演算は循環シフトで、上位方向へ溢れた桁は一番下位の桁へと戻るものとなります。

シフト演算の適用に際して、先ほどの転置で得られたビット列を28ビットで半分に分割し、これを

C_0 = 0000000011111111111111111110 \\
D_0 = 0000011100011000111001110000

とおくこととします。
そしてこのシフト演算を 16回 適用するのですが、「何回目のシフト演算か」によりシフト量が異なります。
シフト量は以下の表の通りです。

何回目?	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
シフト量	1	1	2	2	2	2	2	2	1	2	2	2	2	2	2	1

1度目のシフト演算により

C_1 = 0000000111111111111111111100\\
D_1 = 0000111000110001110011100000

が得られ、この操作を$C_{16}, D_{16}$が求まるまで繰り返します。

コード例については次の説明で示します。

転置2 PC-2

前述したシフト演算により得られる$C_{1\dots 16}, D_{1\dots 16}$それぞれについて、各々を結合した $C_nD_n$に対して以下の転置を適用することで 16個 のサブ鍵 $K_{1\dots 16}$ を得ます。

PC-2

14 17 11 24 1 5 3 28 15 6 21 10 23 19 12 4 26 8 16 7 27 20 13 2 41 52 31 37 47 55 30 40 51 45 33 48 44 49 39 56 34 53 46 42 50 36 29 32

例として一つ目のサブ鍵 $K_1$ は $C_1D_1 = 00000001111111111111111111000000111000110001110011100000$ より $K_1 = 111100001011111011100110000000011110111010101000$ となります。

各シフトにより得られる$C_n,D_n$を利用するので、シフト演算の繰り返し操作と同時に行うといいと思います⁵。

SHIFT.each do |s|
  c << (c.last[s..-1] + c.last[0...s])
  d << (d.last[s..-1] + d.last[0...s])
  @keys << permutate_with_pc2(c.last + d.last)
end

暗号化

サブ鍵を生成したらいよいよ暗号化のプロセスに入ります。
今回は暗号化したい文字列として ddaattaa およびその二進表記 $0110010001100100011000010110000101110100011101000110000101100001$ を用います。

初期転置 IP

入力として与えられたブロックに対し以下の転置を適用します。

IP

58 50 42 34 26 18 10 2 60 52 44 36 28 20 12 4 62 54 46 38 30 22 14 6 64 56 48 40 32 24 16 8 57 49 41 33 25 17 09 1 59 51 43 35 27 19 11 3 61 53 45 37 29 21 13 5 63 55 47 39 31 23 15 7

ddaattaa の二進表記に対して適用すると $1111111100110000001100111100110000000000111111110000000000000000$ となります。
得られた転置後のデータを半分（32ビット）で分割し

L_0 = 11111111001100000011001111001100\\
R_0 =00000000111111110000000000000000

とおきます。

コード例はこんな感じです⁶。

def permutate_with_ip
  IP.map { |index| message_bin.chars[index] }
end

ラウンド関数

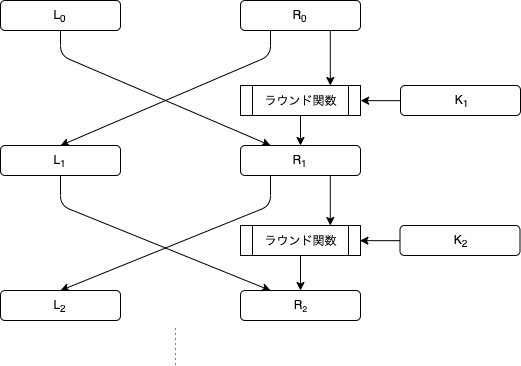
それではDESの要となるラウンド関数について説明していきます。
ラウンド関数を $F$ としたとき、DESにおける処理プロセスは以下の式で表されます（$n = 0\dots 15$、$\oplus$ はXORの意)。

\begin{aligned}
L_{n+1} &= R_n \\
R_{n+1} &= L_n \oplus F(R_n, K_{n+1})
\end{aligned}

$n$ の範囲からわかるようにラウンド関数は 16回 適用します。おそろしい。
図で表すとこのような形です。

このラウンド関数には次の処理が含まれています。

1. 拡大転置Eを$R_n$に対して適用 (32ビット→48ビット)
2. 対応するサブ鍵 $K_{n+1}$ と(1)の結果とのXORをとる (48ビット→48ビット)
3. (2)の結果に対してSボックスを適用 (48ビット→32ビット)
4. (3)の結果を結合したものに対して転置Pを適用 (32ビット→32ビット)

(3)のSボックスの説明は後に譲ることとして、拡大転置E・転置Pおよびサブ鍵とのXORの説明を簡単にしておきます。

拡大転置Eと転置P

拡大転置Eと転置Pは以下のように表されます。

E,P

# E
32 1 2 3 4 5 4 5 6 7 8 9 8 9 10 11 12 13 12 13 14 15 16 17 16 17 18 19 20 21 20 21 22 23 24 25 24 25 26 27 28 29 28 29 30 31 32 1

# P
16 7 20 21 29 12 28 17 1 15 23 26 5 18 31 10 2 8 24 14 32 27 3 9 19 13 30 6 22 11 4 25

コード例も今までの転置とさほど変わらないですね^{7 8}。

# E
def permutate_with_e(r)
  E.map { |index| r[index] }
end

# P
def permutate_with_p(transposed_r)
  P.map { |index| transposed_r[index] }
end

またサブ鍵とのXORについてですが、RubyにおけるXORは他言語と同じく (?) ^ で表現できるため以下のように書きました⁹。

def xor_with_key(permutated_r, key_index)
  r_xor_key = []
  permutated_r
    .zip(keys[key_index])
    .each { |right, key| r_xor_key << (right.to_i ^ key.to_i).to_s }
  r_xor_key
end

あんまりいい書き方ではなさそうですね...

Sボックス

Sボックスも今までに示した転置と同様に「与えられた入力を一定の法則に基づいて並べ換える」操作であることには変わりありません。
ただし単純な転置と異なり、表の中から対応する数値を一つ選択しそれの2進数表記を返すというものとなっています。

この操作の前に、ddaattaa に対し拡大転置Eを適用しサブ鍵 $K_1 = 111100001011111011100110000000011110111010101000$ とのXORをとった結果を $I = 111100001010100100011000100000011110111010101000$ とおきます（用意しておきます）。
この $I$ (48ビット)をまず6ビットごと8つに分割します。

I = 111100\quad 001010\quad 100100\quad 011000\quad 100000\quad 011110\quad 111010\quad 101000

簡単のためそれぞれのビットの塊を $i_n$ としてまとめ

I = i_1 i_2 i_3 i_4 i_5 i_6 i_7 i_8

と表すこととします。
この各々の $i_1 \dots i_8$ 対して $S_1 \dots S_8$ というSボックスをそれぞれ適用します。
具体的には

S_1(i_1)S_2(i_2)S_3(i_3)S_4(i_4)S_5(i_5)S_6(i_6)S_7(i_7)S_8(i_8)

ということです。
お気づきかもしれませんが、このSボックスは 8つ あります。
解説のために $S1$ のみ示します。

$S1$ row\col	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
0	14	4	13	1	2	15	11	8	3	10	6	12	5	9	0	7
1	0	15	7	4	14	2	13	1	10	6	12	11	9	5	3	8
2	4	1	14	8	13	6	2	11	15	12	9	7	3	10	5	0
3	15	12	8	2	4	9	1	7	5	11	3	14	10	0	6	13

Sボックスは入力ビット列における 最初と最後 を合わせたビット列を 行番号とし、残った 中間の4ビット列 を 列番号 とし、対応する数値の 4ビット二進表記 を返す関数のような働きをします。
入力ビット列を $b_1 b_2 b_3 b_4 b_5 b_6$ と表すならば、$(b_1 b_6)_2$ 行 $(b_2 b_3 b_4 b_5)_2$ 列に相当する数値 $y$ の2進表記を返します。

$S1$ へ適用する $i_1 = 111100$ を例にとって説明すると、$10_2$ 行 $1110_2$ 列目すなわち2行14列目に相当する $5_{10}$ の2進表記 $0101_2$ を返します。
この操作を全ての $i_n$ に適用すると結果として

S_1(i_1)S_2(i_2)S_3(i_3)S_4(i_4)S_5(i_5)S_6(i_6)S_7(i_7)S_8(i_8) = 01011011010010110100101101011001

が得られます。

8つあるSボックスはここを参考にしてもらうとして、コード例はこんな感じです⁹。

def transpose_with_s_table(xored_r)
  transposed_r = []
  xored_r.each_slice(6).with_index do |bits, i|
    x = bits[1..4].join.to_i(2)
    y = (bits[0] + bits[-1]).to_i(2)
    transposed_r += DES::S[i][y][x].to_s(2).rjust(4, '0').split('')
  end
  transposed_r
end

最終転置 IPinverse 暗号文

暗号文を得る最後のプロセスとなる最終転置について説明します。

ラウンド関数 $F$ を複数回適用して $L_{16}$ および $R_{16}$ を得ることができました（唐突）。

L_{16} = 10000000100010100101010011100110 \\
R_{16} = 01010101111011001100101000000010

この2つを 左右を逆にして結合 します。
すなわち

R_{16} L_{16} =0101010111101100110010100000001010000000100010100101010011100110

となります。
これに対して下記の最終転置 $IP^{-1}$ を適用します。

ipinverse

40 8 48 16 56 24 64 32 39 7 47 15 55 23 63 31 38 6 46 14 54 22 62 30 37 5 45 13 53 21 61 29 36 4 44 12 52 20 60 28 35 3 43 11 51 19 59 27 34 2 42 10 50 18 58 26 33 1 41 9 49 17 57 25

はい。これにて ddaattaa を kkkeeyyy にて暗号化した暗号文

Encrypted = 0100000000100111010110100011010001001000000100100101111010110110

が得られました
無理やり文字化すると @'Z4H\x12^\xB6 だそうです。読めませんね。

復号?

最後に復号について話します。

ブロック暗号の説明でFeistel構造のはなしをしました。
Feistel構造は 逆変換が自身と同じになる という性質がありました。
そのため、 暗号化のプロセスを全て逆に行うことで平文が得られる ということになります。

結論をいうと、暗号文に対してサブ鍵を $K_1, K_2 \dots K_{15}, K_{16}$ のような昇順ではなく、 $K_{16}, K_{15} \dots K_2, K_1$ のように降順にして適用することで平文が得られます。
不思議ですね...

おしまい

あんまり「つくってまなぶ」要素がなくなってしまいましたね、残念。
まあでも数多あるプログラミング言語はどれも「目的を達成するためのツール」でしかないと思っているので、実装したいものを理解し、実装方針を立てれば自ずと作れるはずですよね...?
今回お話しした「DESをつくる」というものは車輪の再発明になってしまうものの典型ですが、これを機に「他の暗号方式はどんな実装になっているんだろう...?」というような興味をもつ一歩になってくれれば嬉しいですね
RSA暗号とか楕円曲線暗号とかになると多少の数学要素が混じってくるので厳しいものもあるとは思いますが...

あ、Gistを見てくださった方はわかると思うのですが、参考にさせていただいたサイトの数値を使ってテストも書いてあります、TDDで作ってました。
欲しい答えとか欲しい結果が明確な場合にはTDDはさいっこうにキマりますねえ、皆さんもTDDキメていきませんか?

参考文献

• The DES Algorithm Illustrated
  by J. Orlin Grabbe

1. wikipediaより ↩

2. Gist des.rb:131 ↩

3. Gist des_constants.rb:10 ↩

4. Gist des.rb:138 ↩

5. Gist des.rb:85 ↩

6. Gist des.rb:147 ↩

7. Gist des.rb:156 ↩

8. Gist des.rb:183 ↩

9. Gist des.rb:163 ↩ ↩²