ロジスティック関数を描いてみる

Overview

けっこう前に sympy でテイラー展開を描いてみたんですけど、
https://qiita.com/arc279/items/dda101b39b96c4aa94d0

視覚化するとイメージがわきやすいので、
今回はロジスティック回帰に出てくるロジスティック関数を描いてみます。

ロジスティック回帰の詳しい説明はこの辺が詳しいので、以下のサイトの解説と合わせてグラフを眺めてみてください。
http://darden.hatenablog.com/entry/2016/08/22/212522

ここでは数式のちゃんとした説明はしません、というかできないｗ

前準備

$ pip install matplotlib sympy     

以下、jupyterのセルだと思ってください

from sympy import Symbol
from sympy.plotting import plot

p = Symbol('p')
x = Symbol('x')

登場する計算式

\begin{align*}
& {\rm オッズ比 }: \frac{p}{1-p} \\
& {\rm ロジット関数 }: f(p) = \log \frac{p}{1-p} \\
& {\rm ロジスティック関数 }: g(x) = \frac{1}{1+e^{-x}}
\end{align*}

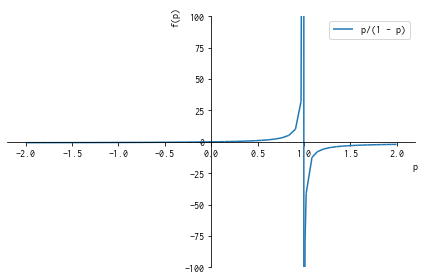
オッズ比(p) = p/(1-p)

jupyter

plot(p/(1-p), (p, -2, 2), ylim=(-100, 100), legend=True)

p = 1 で -inf と +inf が繋がっちゃてるのはご愛嬌なんですが、
これの 0 <= p <= 1 を切り取ると、

jupyter

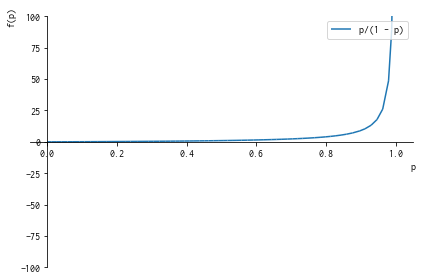
plot(p/(1-p), (p, 0, 1), ylim=(-100, 100), legend=True)

定義域 0 <= p <= 1 に対して 値域が 0 <= オッズ比(p) < +inf まで拡張されます。

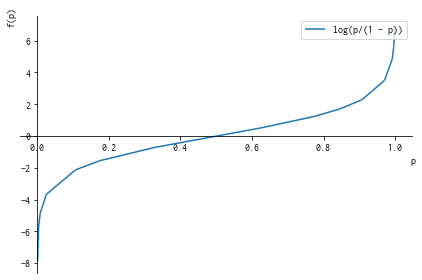
ロジット関数 f(p) = log(p/(1-p))

オッズ比の対数を取ることで、

jupyter

from sympy import log

plot(log(p/(1-p)), legend=True)

オッズ比と同じ定義域に対して、値域が -inf < f(p) < +inf まで拡張されてますね。

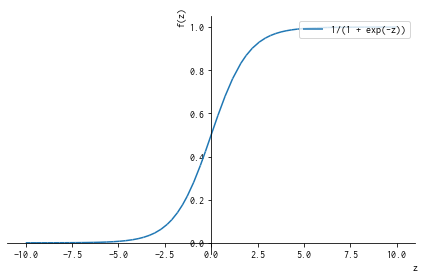
ロジスティック関数 g(x) = 1/(1+exp(-x))

ロジット関数の逆関数なので、

jupyter

from sympy import exp

plot(1/(1+exp(-x)), legend=True)

ロジット関数の値域と定義域が入れ替わって、

• 定義域： -inf < z < +inf
• 値域　： 0 <= g(z) <= 1

つまり、確率 0 <= g(z) <= 1 とみなせる値を出力する関数、と見なせるってことですね。

みたいな解釈で合ってる？