スパイキングニューロンモデル
現在主流の機械学習モデル,ニューラルネットワークは脳の神経細胞を複数結合させたモデルである.
また,神経細胞を数理モデルとして表したモデルを一般的に,人工ニューロンとも言う.
この人工ニューロンには様々なモデルが存在し,現在主流なものは形式ニューロンモデル (McCulloch & Pittsモデル) をベースにした,とてもシンプルなものである.
本記事では,形式ニューロンに加え,さらに詳細に神経細胞の挙動を表現したニューロンモデルをいくつか実装例と一緒に紹介する.
そういった,より詳細に定義されたニューロンモデルは一般的にスパイキングニューロンモデルと呼ばれる.
(正確には,スパイク列と呼ばれる時系列データを扱うニューロンモデル)
また,スパイキングニューロンを使用した人工ニューラルネットワークをスパイキングニューラルネットワークと呼ぶ.
詳しく知りたい人はSpiking Neural Networkとは何なのかを参照.

前提知識
神経細胞は簡単に,以下の挙動や性質を持っている.
これらの挙動や性質をどこまで細かく定義するかが重要となる.
- ニューロンは膜電位と呼ばれる内部状態を持つ
- 膜電位は入力データとシナプス結合荷重(重み)と積和されたものに依存し変化する
- 膜電位がとある閾値(バイアス)を超えたとき発火しスパイクを生成する
形式ニューロンモデル
1943年に提案された最古(?)の人工ニューロンモデル.
別名,McCulloch & Pittsモデル.
やってることは,とてもシンプルだが今のニューラルネットワークでは未だに採用されている.
import numpy as np
class FormalNeuron:
def __init__(self, bias):
"""
形式ニューロンモデル
:param bias: 発火閾値
"""
self.bias = bias
def calc(self, inputs, weights):
"""
入力とシナプス結合荷重を積和し,出力を決定する
:param inputs:
:param weights:
:return: {0, 1}
"""
input_data = np.dot(inputs, weights)
return 1 if input_data > self.bias else 0 # もともとはステップ関数
if __name__ == '__main__':
inputs = np.array([0.5, 0.4, 0.8]) # 入力データの初期化
weights = np.random.rand(3) # シナプス結合荷重(重み)の初期化
# 形式ニューロンを生成し計算
neuron = FormalNeuron(bias=0.5)
out = neuron.calc(inputs, weights)
print(
f'Inputs : {inputs}\n'
f'Weights : {weights}\n'
f'Output : {out}'
)
Inputs : [0.5 0.4 0.8]
Weights : [0.73876939 0.92170289 0.11853329]
Output : 1
ここでは入出力関数 (活性化関数) としてステップ関数を採用しているが,現在のニューラルネットワークではシグモイド関数やReLU関数など様々なものに置き換えられて情報表現の幅を増やしている.
しかし,神経細胞は本来{0,1}データを扱うもの.
現存のニューラルネットワークは,本来の神経細胞の挙動と大きな乖離があることは,知っておくべきだと思う.
LIF: Leaky integrate-and-fire モデル
ここからが本題.
LIFは最もメジャーなスパイキングニューロンモデル.
工学的なSNN研究では7~8割これが使われているのではないだろうか.
これはSpiking Neural Networkとは何なのかでも簡単に紹介しているが,以下の式によって膜電位を計算する.
$$\tau_{m}\frac{dV(t)}{dt}=(-V(t)+E_{rest})+I(t) \ \ \ \ \ \ (1)$$
$$\tau_{i}\frac{dI(t)}{dt}=-I(t)+\sum_{j\in pre}{w_{j}s_{j}(t)} \ \ \ \ \ \ (2)$$
実際,この式の形に止まらず,研究ごとに細かな仕様の違いはあるが,上の式が基本の形となる.
$(1)$式は膜電位$V(t)$を算出するための微分方程式である.
$\tau_{m}$は膜時定数などと呼ばれ,膜電位が時間経過によって静止膜電位$E_{rest}$に減衰する程度を司る.
$I(t)$は入力電流で,この定義は様々あるが今回は$(2)$式で示すように,入力スパイク$s(t)$に対して重みを積和し,膜電位と同じく時間減衰を伴う形とした.
実際にグラフ描画してみるとわかるが,$(2)$の計算は$s(t)* e^{-t/\tau_{i}}$という,デジタル信号の畳み込み演算をやっていることと同義であることがわかる.
この膜電位がとある発火閾値を超えると,ニューロンの膜電位は急上昇し,それを**発火 (fire)と呼ぶ.
そして突出した部分をスパイク (spike)**と呼ぶ.
実際にPythonで実装して,挙動を見てみよう.
import numpy as np
import matplotlib.pyplot as plt
class LIF:
def __init__(self, rest: float = -65, ref: float = 3, th: float = -40, tc: float = 20, peak: float = 20):
"""
Leaky integrate-and-fire neuron
:param rest: 静止膜電位 [mV]
:param ref: 不応期 [ms]
:param th: 発火閾値 [mV]
:param tc: 膜時定数 [ms]
:param peak: ピーク電位 [mV]
"""
self.rest = rest
self.ref = ref
self.th = th
self.tc = tc
self.peak = peak
def calc(self, inputs, weights, time=300, dt=0.5, tci=10):
"""
膜電位を計算する.
本来はスパイク時刻(発火時刻)も保持しておいてそれを出力データとする.
:param inputs:
:param weights:
:param time:
:param dt:
:param tci:
:return:
"""
i = 0 # 初期入力電流
v = self.rest # 初期膜電位
tlast = 0 # 最後に発火した時刻
monitor = [] # 膜電位の記録
for t in range(int(time/dt)):
# 入力電流の計算
di = ((dt * t) > (tlast + self.ref)) * (-i + np.sum(inputs[:, t] * weights))
i += di * dt / tci
# 膜電位の計算
dv = ((dt * t) > (tlast + self.ref)) * ((-v + self.rest) + i)
v += dv * dt / self.tc
# 発火処理
tlast = tlast + (dt * t - tlast) * (v >= self.th) # 発火したら発火時刻を記録
v = v + (self.peak - v) * (v >= self.th) # 発火したら膜電位をピークへ
monitor.append(v)
v = v + (self.rest - v) * (v >= self.th) # 発火したら静止膜電位に戻す
return monitor
if __name__ == '__main__':
time = 300 # 実験時間 (観測時間)
dt = 0.5 # 時間分解能
pre = 50 # 前ニューロンの数
inputs = np.zeros((pre, int(time/dt))) # 入力スパイク列の初期化
for i in inputs:
i[::np.random.randint(10, 100)] = 1 # 適当にスパイクを等間隔で立ててみる
i[0] = 0 # 最初のindexは0にしておく (なんとなく気持ち悪いから)
# 重みの初期化
weights = np.random.rand(pre) + 20. # 今回は前ニューロン数少なめなので大きめな重みにしておく
neuron = LIF()
v = neuron.calc(inputs, weights)
# 結果の描画
plt.figure(figsize=(12, 4))
# 入力データ
plt.subplot(1, 2, 1)
t = np.arange(0, time, dt)
spikes = [t[i == 1] for i in inputs]
for i, s in enumerate(spikes):
plt.scatter(s, [i for _ in range(len(s))], s=5.0, c='tab:blue')
plt.xlim(0, time)
plt.ylim(-1, pre)
plt.xlabel('time [ms]')
plt.ylabel('Neuron index')
# 膜電位
plt.subplot(1, 2, 2)
plt.plot(t, v)
plt.xlabel('time [ms]')
plt.ylabel('Membrane potential [mV]')
plt.show()
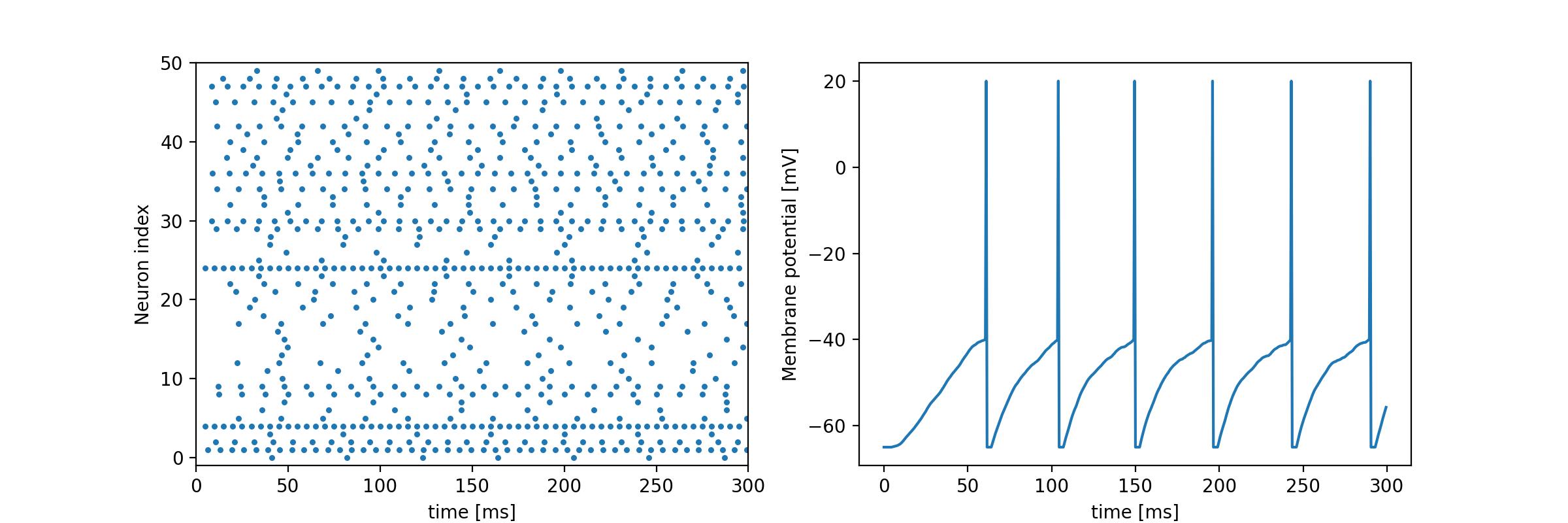
実装例としてはこんな感じになる.
グラフ左が前ニューロンからの入力スパイク列をラスタープロットしたもので,グラフ右はその入力を受け取った**ニューロンの膜電位(内部状態)**を描画している.
これだけだと,工学的なモデル構築をするにはいろいろと足りないが,LIFモデルの挙動は確認できるはず.
ちなみに,膜電位の突出したところがスパイクである.
形式ニューロンと比べ,複雑度がかなり増していることもわかるだろう.
なんといっても,時間次元を持っているのだから...
Hodgkin-Huxley モデル
先ほどのLIFモデルより,かなり精緻に挙動を数理モデルに落とし込んだもの.
Hodgkin-Huxleyニューロンモデルを実装してみるで紹介しているので,詳細はここでは書かないが,簡単に紹介する.
我々の脳内の神経細胞は,先ほどのLIFモデルからもわかるように一種の充電回路のような挙動を取る.
その際,時間的な漏れはカリウムイオンやナトリウムイオンなど様々なイオンの細胞内外への出入りによって発生する.
そのイオンの移動を細かく定義したものがHHモデルである.
現存のニューロンモデルの中では最も変態なモデル.
主に,脳科学者・神経科学者向けのモデルで,ただの工学屋さんが使用することはほとんど無いだろう.
import numpy as np
import matplotlib.pyplot as plt
class HodgkinHuxley:
def __init__(self, time, dt, rest=-65., Cm=1.0, gNa=120., gK=36., gl=0.3, ENa=50., EK=-77., El=-54.387):
"""
Initialize Neuron parameters
:param time: experimental time
:param dt: time step
:param rest: resting potential
:param Cm: membrane capacity
:param gNa: Na+ channel conductance
:param gK: K+ channel conductance
:param gl: other (Cl) channel conductance
:param ENa: Na+ equilibrium potential
:param EK: K+ equilibrium potential
:param El: other (Cl) equilibrium potentials
"""
self.time = time
self.dt = dt
self.rest = rest
self.Cm = Cm
self.gNa = gNa
self.gK = gK
self.gl = gl
self.ENa = ENa
self.EK = EK
self.El = El
def calc(self, i):
""" compute membrane potential """
# initialize parameters
v = self.rest
n = 0.32
m = 0.05
h = 0.6
v_monitor = []
n_monitor = []
m_monitor = []
h_monitor = []
time = int(self.time / self.dt)
# update time
for t in range(time):
# calc channel gating kinetics
n += self.dn(v, n)
m += self.dm(v, m)
h += self.dh(v, h)
# calc tiny membrane potential
dv = (i[t] -
self.gK * n**4 * (v - self.EK) - # K+ current
self.gNa * m**3 * h * (v - self.ENa) - # Na+ current
self.gl * (v - self.El)) / self.Cm # other current
# calc new membrane potential
v += dv * self.dt
# record
v_monitor.append(v)
n_monitor.append(n)
m_monitor.append(m)
h_monitor.append(h)
return v_monitor, n_monitor, m_monitor, h_monitor
def dn(self, v, n):
return (self.alpha_n(v) * (1 - n) - self.beta_n(v) * n) * self.dt
def dm(self, v, m):
return (self.alpha_m(v) * (1 - m) - self.beta_m(v) * m) * self.dt
def dh(self, v, h):
return (self.alpha_h(v) * (1 - h) - self.beta_h(v) * h) * self.dt
def alpha_n(self, v):
return 0.01 * (10 - (v - self.rest)) / (np.exp((10 - (v - self.rest))/10) - 1)
def alpha_m(self, v):
return 0.1 * (25 - (v - self.rest)) / (np.exp((25 - (v - self.rest))/10) - 1)
def alpha_h(self, v):
return 0.07 * np.exp(-(v - self.rest) / 20)
def beta_n(self, v):
return 0.125 * np.exp(-(v - self.rest) / 80)
def beta_m(self, v):
return 4 * np.exp(-(v - self.rest) / 18)
def beta_h(self, v):
return 1 / (np.exp((30 - (v - self.rest))/10) + 1)
if __name__ == '__main__':
# init experimental time and time-step
time = 300 # 実験時間 (観測時間)
dt = 2**-4 # 時間分解能 (HHモデルは結構小さめでないと上手く計算できない)
# Hodgkin-Huxley Neuron
neuron = HodgkinHuxley(time, dt)
# 入力データ (面倒臭いので適当な矩形波とノイズを合成して作った)
input_data = np.sin(0.5 * np.arange(0, time, dt))
input_data = np.where(input_data > 0, 20, 0) + 10 * np.random.rand(int(time/dt))
input_data_2 = np.cos(0.3 * np.arange(0, time, dt) + 0.5)
input_data_2 = np.where(input_data_2 > 0, 10, 0)
input_data += input_data_2
# 膜電位などを計算
v, m, n, h = neuron.calc(input_data)
# plot
plt.figure(figsize=(12, 6))
x = np.arange(0, time, dt)
plt.subplot(3, 1, 1)
plt.title('Hodgkin-Huxley Neuron model Simulation')
plt.plot(x, input_data)
plt.ylabel('I [μA/cm2]')
plt.subplot(3, 1, 2)
plt.plot(x, v)
plt.ylabel('V [mV]')
plt.subplot(3, 1, 3)
plt.plot(x, n, label='n')
plt.plot(x, m, label='m')
plt.plot(x, h, label='h')
plt.xlabel('time [ms]')
plt.ylabel('Conductance param')
plt.legend()
plt.show()
コードが長すぎて読むのが嫌になってしまうが,挙動を見てみるとしっかりと膜電位と発火の様子がうかがえる.
LIFモデルでは発火閾値を静的に決定して,かなり力技でニューロンを発火させていたが,HHモデルでは発火閾値を明確に定義しなくともニューロンの挙動をイオンの出入りだけで表現できている.
詳しくは先ほどのリンクからどうぞ.
Izhikevichモデル
2003年に提案された比較的新しいニューロンモデル.
筆者は一番好き.
Izhikevichニューロンは以下の2つの微分方程式からなる.
4つのハイパーパラメータ$(a,b,c,d)$と,4つの変数$(v,t,u,I)$から成り立っている.
個人的にはすごく美しいと思う.
$$\frac{dv}{dt}=0.04v^{2} + 5v + 140 -u + I$$
$$\frac{du}{dt}=a(bv-u)$$
$${\rm if}\ \ v\geq30,\ \ {\rm then}\ \ v\leftarrow c,\ u\leftarrow u+d$$
HHモデルよりシンプルでありながら,4つのパラメータの組み合わせで,様々なニューロンの挙動を模倣できるため,近年多くの研究で見かけるようになった.
import numpy as np
import matplotlib.pyplot as plt
class Izhikevich:
def __init__(self, a, b, c, d):
"""
Izhikevich neuron model
:param a: uのスケーリング係数
:param b: vに対するuの感受性度合い
:param c: 静止膜電位
:param d: 発火後の膜電位が落ち着くまでを司る係数
"""
self.a = a
self.b = b
self.c = c
self.d = d
def calc(self, inputs, weights, time=300, dt=0.5, tci=10):
"""
膜電位(Membrane potential) v と回復変数(Recovery variable) u を計算する
:param inputs:
:param weights:
:param time:
:param dt:
:param tci:
:return:
"""
v = self.c
u = self.d
i = 0
monitor = {'v': [], 'u': []}
for t in range(int(time/dt)):
# 入力電流を計算
di = -i + np.sum(inputs[:, t] * weights)
i += di * dt / tci
# uを計算
du = self.a * (self.b * v - u)
u += du * dt
monitor['u'].append(u)
# vを計算
dv = 0.04 * v**2 + 5 * v + 140 - u + i
v += dv * dt
monitor['v'].append(v)
# 発火処理
if v >= 30:
v = self.c
u += self.d
return monitor
if __name__ == '__main__':
time = 300 # 実験時間 (観測時間)
dt = 0.5 # 時間分解能
pre = 50 # 前ニューロンの数
inputs = np.zeros((pre, int(time / dt))) # 入力スパイク列の初期化
for i in inputs:
i[::np.random.randint(10, 100)] = 1 # 適当にスパイクを等間隔で立ててみる
i[0] = 0 # 最初のindexは0にしておく (なんとなく気持ち悪いから)
# 重みの初期化
weights = np.random.rand(pre) + 20. # 今回は前ニューロン数少なめなので大きめな重みにしておく
# Izhikevichニューロンの生成 (今回はRegular Spiking Neuronのパラメータ)
neuron = Izhikevich(
a=0.02,
b=0.2,
c=-65,
d=8
)
history = neuron.calc(inputs, weights, time=time, dt=dt)
# 結果の描画
plt.figure(figsize=(12, 8))
# 入力データ
plt.subplot(3, 1, 1)
t = np.arange(0, time, dt)
spikes = [t[i == 1] for i in inputs]
for i, s in enumerate(spikes):
plt.scatter(s, [i for _ in range(len(s))], s=5.0, c='tab:blue')
plt.xlim(0, time)
plt.ylim(-1, pre)
plt.ylabel('Neuron index')
# 膜電位
plt.subplot(3, 1, 2)
plt.plot(t, history['v'])
plt.ylabel('Membrane potential $v$ [mV]')
# 膜電位
plt.subplot(3, 1, 3)
plt.plot(t, history['u'], c='tab:orange')
plt.xlabel('time [ms]')
plt.ylabel('Recovery variable $u$')
plt.show()
こちらも,HHと同様に発火については発火閾値を設けずとも,膜電位の挙動を再現できている.
ただし,静止膜電位へ戻す部分については強引である.
Izhikevichニューロンについては,Web上で動作するシミュレータを前に作ったのでぜひ遊んでみて欲しい.
Izhikevich Neuron Simulator - Web上で動作するニューロンシミュレータ
まとめ
今回は,4つの代表的な人工ニューロンモデルについて紹介した.
他にもニューロンモデルは存在するが,各モデルともメリットデメリットが存在する.
それは,計算量と生物学的妥当性のトレードオフであり,以下の図でそれを示している.

HHモデルは生物学的妥当性はかなり強いものの,コードをみてわかるようにかなりの計算量である.
それに比べてLIFモデルは少ない計算量で挙動を確認できるが,生物学的妥当性は(比較的)劣る.
どのニューロンモデルを使用するかは,その研究が工学的な立場か,はたまた生物学的な立場かに依存するでしょう.
とまあ,ここまで色々と真面目に(?)紹介してきたが,これを機に神経科学やSNN研究に興味を持ってくれる人が増えたら嬉しい限りです.
おしまい.