はじめに
複数の物体をばねに繋げた系を考える。このような系は複雑な振動をすることが知られている。しかし、よくよく見ると正弦波の重ね合わせで表現することができる。
そこで、今回はこのような複雑な運動(連成振動)について考察してみる。
具体的には、まずは運動方程式を立式し、行列式を用いて座標変換のような操作を行う。
その後、質点の座標が単振動の合成和で表現されることを示す。
次に、Pythonを用いた数値計算により実際の運動の様子を微分方程式からシミュレーションする。
問題設定
以下のような系を考える。ただし、ばね定数,自然長は$k,l$で共通であるとする。
運動方程式
まず、質点$A,B$について以下のような運動方程式を立てる。
\begin{equation}
\left\{ \,
\begin{aligned}
& m_A \frac{d^2 x_A}{dt^2} = k(x_B-x_A-l)-k(x_A-l) \\
& m_B \frac{d^2 x_A}{dt^2} = k(L-x_B-l)-k(x_B-x_A-l) \\
\end{aligned}
\right.
\end{equation}
ゆえに、
\begin{equation}
\left\{ \,
\begin{aligned}
& m_A \frac{d^2 x_A}{dt^2} = k(x_B-2 x_A) \\
& m_B \frac{d^2 x_A}{dt^2} = k(-2 x_B+x_A+L) \\
\end{aligned}
\right.
\end{equation}
したがって、行列で表すと以下のようになる。
\begin{bmatrix}
m & 0 \\
0 & m
\end{bmatrix}
\begin{bmatrix}
\frac{d^2 x_A}{dt^2} \\
\frac{d^2 x_B}{dt^2} \\
\end{bmatrix}
=
-
\begin{bmatrix}
2k & -k \\
-k & 2k
\end{bmatrix}
\begin{bmatrix}
x_A \\
x_B\\
\end{bmatrix}
+
\begin{bmatrix}
0 \\
kL\\
\end{bmatrix}
さらに、定数に気を付けると以下のようになる。
\begin{bmatrix}
m & 0 \\
0 & m
\end{bmatrix}
\begin{bmatrix}
\frac{d^2 x_A}{dt^2} \\
\frac{d^2 x_B}{dt^2} \\
\end{bmatrix}
=
-
\begin{bmatrix}
2k & -k \\
-k & 2k
\end{bmatrix}
\begin{bmatrix}
x_A -\frac{L}{3}\\
x_B -\frac{2L}{3}\\
\end{bmatrix}
ここで、
\textbf{M}=
\begin{bmatrix}
m & 0 \\
0 & m
\end{bmatrix}
,
\textbf{K}=
\begin{bmatrix}
2k & -k \\
-k & 2k
\end{bmatrix}
であるとする。
つまり、
\textbf{M}\frac{d^2\textbf{X}}{dt^2}=-\textbf{K}\textbf{X}
ただし、
\textbf{X}=
\begin{bmatrix}
x_A -\frac{L}{3}\\
x_B -\frac{2L}{3}\\
\end{bmatrix}
対角化
固有値と固有ベクトル
$\textbf{K}$を対角化する。固有ベクトル$\textbf{A}$を考える。
\textbf{K}\textbf{A}=\lambda \textbf{A}
(\textbf{K}-\lambda \textbf{I}) \textbf{A}=0
この方程式が、$\textbf{A}=0$以外の解をもつためには、以下の条件が必要である。
|\textbf{K}-\lambda \textbf{I}|=0
したがって、
\begin{vmatrix}
2k-\lambda & -k \\
-k & 2k-\lambda
\end{vmatrix}
=0
(2k-\lambda)^2-k^2
=0
\lambda = k,3k
したがって、
$\lambda = k$のとき、固有ベクトルは、
\begin{bmatrix}
1 \\
1 \\
\end{bmatrix}
$\lambda=3k$のとき、固有ベクトルは、
\begin{bmatrix}
1 \\
-1 \\
\end{bmatrix}
したがって、
\begin{bmatrix}
1 & 1 \\
1 & -1
\end{bmatrix}^T
\begin{bmatrix}
2k & -k \\
-k & 2k
\end{bmatrix}
\begin{bmatrix}
1 & 1 \\
1 & -1
\end{bmatrix}
=
\begin{bmatrix}
k & 0 \\
0 & 3k
\end{bmatrix}
ところで、
\begin{bmatrix}
1 & 1 \\
1 & -1
\end{bmatrix}^T
\begin{bmatrix}
m & 0 \\
0 & m \\
\end{bmatrix}
\begin{bmatrix}
1 & 1 \\
1 & -1
\end{bmatrix}
=
\begin{bmatrix}
m & 0 \\
0 & m
\end{bmatrix}
となる。ここで、
解法
P=\begin{bmatrix}
1 & 1 \\
1 & -1
\end{bmatrix}
とすると、運動方程式は
\textbf{M}\frac{d^2\textbf{X}}{dt^2}=-\textbf{K}\textbf{X}
となることから、
\textbf{X}=\textbf{P}\textbf{X'}
という変換式を用いると以下のようになる。
\textbf{M}\frac{d^2\textbf{P X'}}{dt^2}=-\textbf{K}(P\textbf{X'})
(P^{T}\textbf{M}P)\frac{d^2\textbf{ X'}}{dt^2}=-(P^{T}\textbf{K}P)\textbf{X'}
\begin{bmatrix}
m & 0 \\
0 & m
\end{bmatrix}
\frac{d^2\textbf{X}}{dt^2}
=
-
\begin{bmatrix}
k & 0 \\
0 & 3k
\end{bmatrix}
\textbf{X}
\textbf{X'}=
\begin{bmatrix}
A \sin {\omega_1 (t-\alpha)} \\
B \sin {\omega_2 (t-\beta)} \\
\end{bmatrix}
ただし、
\omega_1=\sqrt{\frac{k}{m}},\omega_2=\sqrt{\frac{3k}{m}}
したがって、
\textbf{X}=
\begin{bmatrix}
1 & 1 \\
1 & -1
\end{bmatrix}^{T}
\begin{bmatrix}
C_1 \sin {\omega_1 (t-\alpha)} \\
C_2 \sin {\omega_2 (t-\beta)} \\
\end{bmatrix}
ただし、$C_1,C_2,\alpha,\beta$は初期条件によって決定される任意定数である。
ゆえに、
x_A=C_1 \sin {\omega_1 (t-\alpha)}+C_2 \sin {\omega_2 (t-\beta)}+\frac{L}{3}
x_B=C_1 \sin {\omega_1 (t-\alpha)}-C_2 \sin {\omega_2 (t-\beta)}+\frac{2L}{3}
したがって、重心の座標は以下のようになる。
x_G=C_1 \sin {\omega_1 (t-\alpha)}
このように、重心は単振動をすることがわかる。
一方で、重心からみた$A,B$の運動の様子を考える。
x_A-x_G=C_2 \sin {\omega_2 (t-\beta)}
x_B-x_G=-C_2 \sin {\omega_2 (t-\beta)}
このように、重心$G$からみた$A,B$も単振動をすることがわかる。
プログラム
上記の考察が正しいか確認するためにプログラムを作成した。
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
import math
#微小時間
dt=1e-5
#ばね定数
k=10
#質量
m_A=1
m_B=1
#初期位置
x_A=0
x_B=2
#初速度
v_A=1
v_B=1
#自然長
l=0.5
L=3
x_A_ary=[]
x_B_ary=[]
x_G_ary=[]
v_A_ary=[]
v_B_ary=[]
v_G_ary=[]
a_A_ary=[]
a_B_ary=[]
a_G_ary=[]
U_ary=[]
K_ary=[]
t_ary=[]
t=0
while(t<10):
a_A=k*(x_B-2*x_A)/m_A
a_B=k*(-2*x_B+x_A+L)/m_B
x_A_ary.append(x_A)
x_B_ary.append(x_B)
x_G_ary.append((m_A*x_A+m_B*x_B)/(m_A+m_B))
v_A_ary.append(v_A)
v_B_ary.append(v_B)
v_G_ary.append((m_A*v_A+m_B*v_B)/(m_A+m_B))
a_A_ary.append(a_A)
a_B_ary.append(a_B)
a_G_ary.append((m_A*a_A+m_B*a_B)/(m_A+m_B))
U=0.5*k*(x_A-l)**2+0.5*k*(x_B-x_A-l)**2+0.5*k*(L-x_B-l)**2
K=0.5*m_A*v_A**2+0.5*m_B*v_B**2
U_ary.append(U)
K_ary.append(K)
t_ary.append(t)
v_A=v_A+a_A*dt
v_B=v_B+a_B*dt
x_A=x_A+v_A*dt
x_B=x_B+v_B*dt
t=t+dt
plt.plot(t_ary,x_A_ary,label="A",color="red")
plt.plot(t_ary,x_B_ary,label="B",color="blue")
plt.plot(t_ary,x_G_ary,label="G",color="black")
plt.xlabel("時刻")
plt.ylabel("位置")
plt.legend()
plt.savefig("2物体連成問題_ばね.png")
plt.show()
x_A_ary=np.array(x_A_ary)
x_B_ary=np.array(x_B_ary)
x_G_ary=np.array(x_G_ary)
plt.plot(t_ary,x_A_ary-x_G_ary,label="x_A-x_G",color="red")
plt.plot(t_ary,x_B_ary-x_G_ary,label="x_B-x_G",color="blue")
plt.xlabel("時刻")
plt.ylabel("位置")
plt.legend()
plt.savefig("2物体連成問題_重心からの位置_ばね.png")
plt.show()
plt.plot(K_ary,U_ary)
plt.xlabel("系全体の運動エネルギー")
plt.ylabel("系全体の位置エネルギー")
plt.savefig("エネルギー.png")
plt.show()
plt.plot(x_G_ary,v_G_ary)
plt.xlabel("重心の位置")
plt.ylabel("重心の速度")
plt.savefig("重心の位置と速度の関係性.png")
plt.show()
結果
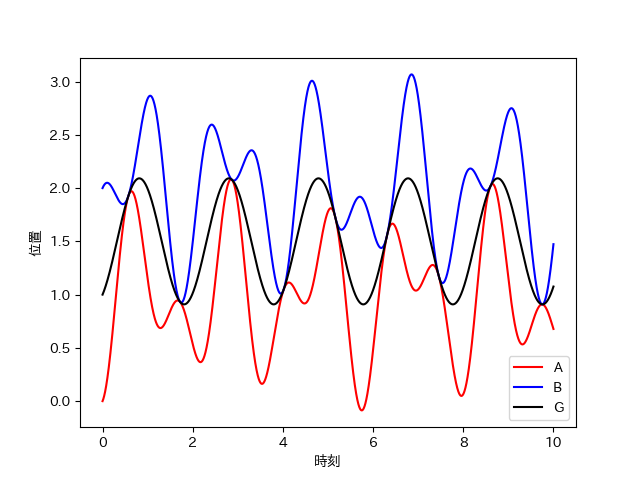
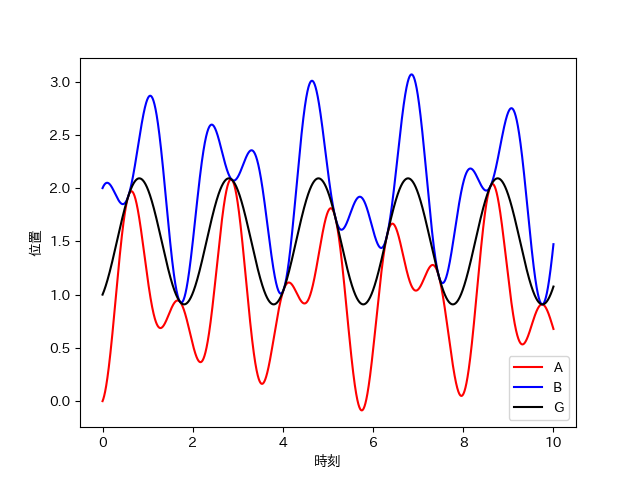
A,Bの位置
このように、A,Bは複雑な運動をするが、Gは単振動をする。
重心からみたA,Bの位置
GからみるとA,Bは単振動をする。
重心の位置と速度の関係性
Gは単振動をしていることがわかる。
系全体のエネルギー
系全体のエネルギーは保存されている。
まとめ
今回は、微分方程式を行列を用いて考察してみた。
具体的には、連成振動をする系に対して微分方程式を作成した。
その後、行列の式で微分方程式を表した。そして、対角化を用いて微分方程式を解いた。
後半では、その解が正しいことをPythonを用いた数値計算で確認した。
固有値や対角化は系の安定性の議論にも使用されるため、制御工学でも頻出な概念である。
苦手意識が多い分野であるので、今回の題材をもとに復習するべきである。