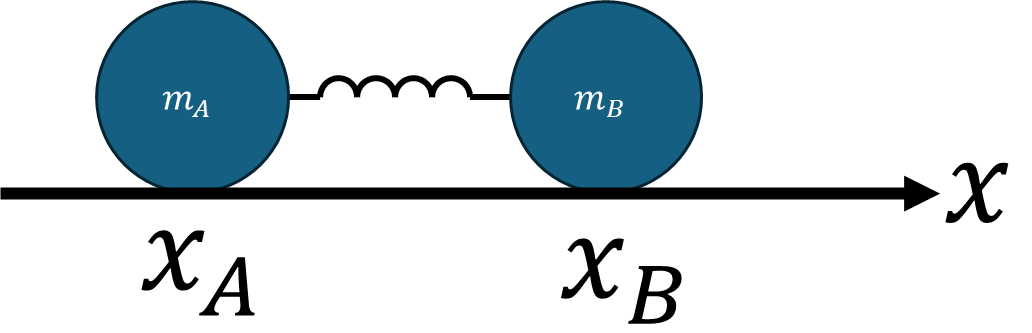はじめに
2物体の運動を同時に考察する問題は、2物体問題と言われている。2物体問題は、大学受験では、難問に分類されがちだが、かなり本質的な問題である。
一般に、2つの物体の重心の運動と重心からみた相対運動を合成することで、運動の様子を知ることができる。
そこで今回は、運動方程式から出発して、2つの物体がどのような運動をするのかを調査する。
問題設定
以下のような、2つの質点をばねが連結している系を考える。
この系の物体$A,B$に適当な初速度を与えたとき、$A,B$がどのような運動をするのか調査する。ただし、ばねの自然長を$l$とする。
まず、以下のような運動方程式を考える。
\begin{equation}
\left\{ \,
\begin{aligned}
& m_A \frac{d^2 x_A}{dt^2} = k(x_B-x_A-l) \\
& m_B \frac{d^2 x_B}{dt^2} = -k(x_B-x_A-l) \\
\end{aligned}
\right.
\end{equation}
2つの運動方程式を足すと以下の関係が得られる。
m_A \frac{d^2 x_A}{dt^2}+m_B \frac{d^2 x_B}{dt^2} =0
したがって、
\frac{d^2 }{dt^2}(m_A x_A+m_B x_B) =0
\frac{d}{dt}(m_A x_A+m_B x_B)=C
ただし$C$は定数である。これは、運動量保存則を示している。
一方で、2つの運動方程式の差は以下のようになる。
\begin{equation}
\left\{ \,
\begin{aligned}
& \frac{d^2 x_A}{dt^2} = \frac{k(x_B-x_A-l) }{m_A}\\
& \frac{d^2 x_B}{dt^2} = -\frac{k(x_B-x_A-l)}{m_B} \\
\end{aligned}
\right.
\end{equation}
\frac{d^2}{dt^2}(x_B-x_A)=-\frac{k}{M}(x_B-x_A)
ここで、$M$(換算質量)は以下のように与えられる。
M=\frac{m_A m_B}{m_A+m_B}
したがって、$x_B-x_A$は以下のように表すことができる。
x_B-x_A=C_1 \sin (\omega t +\alpha)
ただし、$C_1,\alpha$は初期条件によって決まる定数である。また、
\omega =\sqrt{\frac{k}{M}}
ところで、
\frac{d}{dt}(m_A x_A+m_B x_B)=C
より、
m_A x_A+m_B x_B =C t+C_2
と合わせると、以下のようになる。
\begin{equation}
\left\{ \,
\begin{aligned}
& x_A = -\frac{m_B}{m_A+m_B} C_1 \sin (\omega t +\alpha) +\frac{Ct+C_2}{m_A+m_B}\\
& x_B = \frac{m_A}{m_A+m_B} C_1 \sin (\omega t +\alpha) +\frac{Ct+C_2} {m_A+m_B}\\
\end{aligned}
\right.
\end{equation}
ここで、重心を以下のように定義する。
x_G=\frac{m_A x_A+m_B x_B}{m_A+m_B}
ここで、
\frac{d}{dt}(m_A x_A+m_B x_B)=C
より、
x_G=\frac{Ct+C_2} {m_A+m_B}
となる。したがって
重心からみた、A,Bの運動は単振動をする。一方で、重心自体は等速直線運動をする。
プログラム
以下のようなプログラムを作成した。
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
import math
#微小時間
dt=1e-5
#ばね定数
k=10
#質量
m_A=1
m_B=1
#初期位置
x_A=0
x_B=2
#初速度
v_A=1
v_B=1
#自然長
l=1
x_A_ary=[]
x_B_ary=[]
x_G_ary=[]
v_A_ary=[]
v_B_ary=[]
v_G_ary=[]
a_A_ary=[]
a_B_ary=[]
a_G_ary=[]
t_ary=[]
t=0
while(t<10):
a_A=k*((x_B-x_A)-l)/m_A
a_B=-k*((x_B-x_A)-l)/m_B
x_A_ary.append(x_A)
x_B_ary.append(x_B)
x_G_ary.append((m_A*x_A+m_B*x_B)/(m_A+m_B))
v_A_ary.append(v_A)
v_B_ary.append(v_B)
v_G_ary.append((m_A*v_A+m_B*v_B)/(m_A+m_B))
a_A_ary.append(a_A)
a_B_ary.append(a_B)
a_G_ary.append((m_A*a_A+m_B*a_B)/(m_A+m_B))
t_ary.append(t)
v_A=v_A+a_A*dt
v_B=v_B+a_B*dt
x_A=x_A+v_A*dt
x_B=x_B+v_B*dt
t=t+dt
plt.plot(t_ary,x_A_ary,label="A",color="red")
plt.plot(t_ary,x_B_ary,label="B",color="blue")
plt.plot(t_ary,x_G_ary,label="G",color="black")
plt.xlabel("時刻")
plt.ylabel("位置")
plt.legend()
plt.savefig("2物体問題_ばね.png")
plt.show()
x_A_ary=np.array(x_A_ary)
x_B_ary=np.array(x_B_ary)
x_G_ary=np.array(x_G_ary)
plt.plot(t_ary,x_A_ary-x_G_ary,label="x_A-x_G",color="red")
plt.plot(t_ary,x_B_ary-x_G_ary,label="x_B-x_G",color="blue")
plt.xlabel("時刻")
plt.ylabel("位置")
plt.legend()
plt.savefig("2物体問題_重心からの位置_ばね.png")
plt.show()
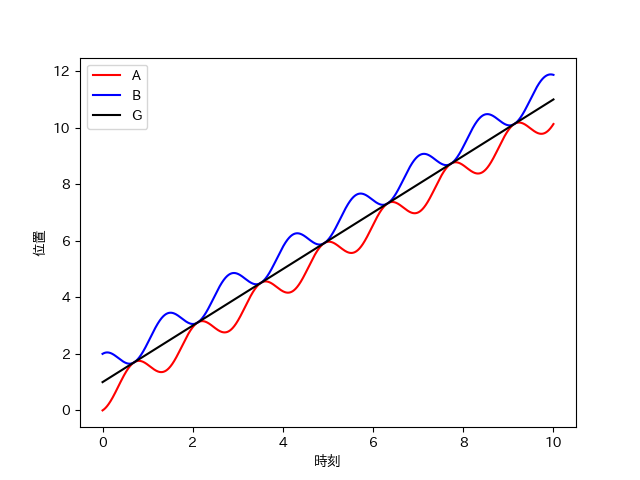
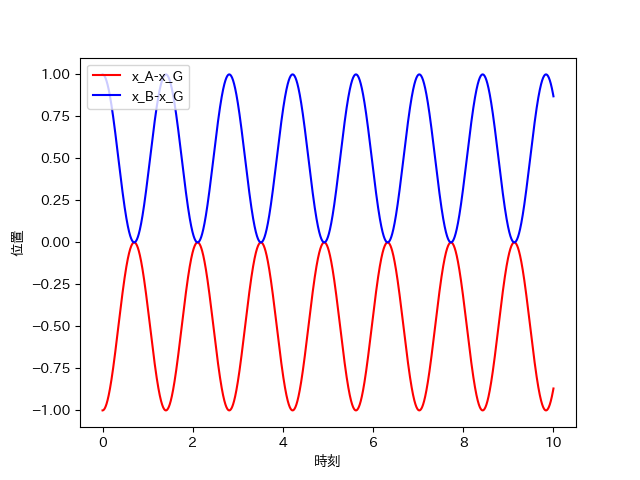
以下のようなグラフが出力される。
このように、重心は等速直線運動をすることがわかる。
一方で、重心からみたA,Bの運動の様子も示す。
このように、重心から見るとA,Bは単振動をしていることがわかる。
まとめ
今回は、受験物理で必須の2物体問題を扱った。2物体問題は、難しいとされがちだが、系の重心を考えることで、単純な運動の合成として2つの物体の運動を叙述することができる。
前半では、如何にして運動方程式から運動の様子を導出するのかを学んだ。
また、後半では、その計算が正しいか確認するため、計算機を用いて数値計算を行った。