この記事で紹介させていただくこと
iris データセットを用いて、scikit-learn の様々な機械学習分類アルゴリズムを試してみた記事です。まず、 iris データセットの説明を行い、次に各分類手法を試していきます。
やっていて感じたのは、scikit-learn は入門用の教材として、とてもとっつきやすかったです。また、書籍『Python ではじめる機械学習 scikit-learn で学ぶ特徴量エンジニアリングと機械学習の基礎』が教科書としてとても役立ちました!
iris データセット
データセットのロード
load_iris 関数でロードできます。
from sklearn.datasets import load_iris
iris = load_iris()
データセットの説明
データセットの説明は DESCR (description) から見ることができます。
>>> print(iris.DESCR)
Iris Plants Database
====================
Notes
-----
Data Set Characteristics:
:Number of Instances: 150 (50 in each of three classes)
:Number of Attributes: 4 numeric, predictive attributes and the class
:Attribute Information:
- sepal length in cm
- sepal width in cm
- petal length in cm
- petal width in cm
- class:
- Iris-Setosa
- Iris-Versicolour
- Iris-Virginica
・・・(以下略)
なお、各 Attribute の意味は次の通りです。
| Attribute | 説明 |
|---|---|
| sepal length | ガクの長さ |
| sepal width | ガクの幅 |
| petal length | 花弁の長さ |
| petal width | 花弁の幅 |
データセットの内容
データセットの形状
特徴量は 4 個で、150 個のデータポイントからなります。形状は shape で確認できます。
>>> iris.data.shape
(150, 4)
花の種類
target_names に花の種類が格納されています。次の 3 種です。
>>> print(iris.target_names)
['setosa' 'versicolor' 'virginica']
サンプル
先頭 5 個のサンプルを見てみます。
iris.data には 4 つの特徴量(ガクの長さ、幅、花弁の長さ、幅)が格納されています。
iris.target には種類が格納されています。0(=setosa), 1(=versicolor), 2(=virginica) のいずれかです。
>>> for data, target in zip(iris.data[:5], iris.target[:5]):
... print(data, target)
[ 5.1 3.5 1.4 0.2] 0
[ 4.9 3. 1.4 0.2] 0
[ 4.7 3.2 1.3 0.2] 0
[ 4.6 3.1 1.5 0.2] 0
[ 5. 3.6 1.4 0.2] 0
データを眺める
データフレーム
データフレームにしておくと、データを扱いやすくなります。target の行が 0, 1, 2 だと分かりにくいので種類名に置き換えます。
import pandas as pd
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df['target'] = iris.target
df.loc[df['target'] == 0, 'target'] = "setosa"
df.loc[df['target'] == 1, 'target'] = "versicolor"
df.loc[df['target'] == 2, 'target'] = "virginica"
ざっくり眺めるには describe です。平均値、最小、最大値が分かります。
df.describe()
| sepal length (cm) | sepal width (cm) | petal length (cm) | petal width (cm) | |
|---|---|---|---|---|
| count | 150.000000 | 150.000000 | 150.000000 | 150.000000 |
| mean | 5.843333 | 3.054000 | 3.758667 | 1.198667 |
| std | 0.828066 | 0.433594 | 1.764420 | 0.763161 |
| min | 4.300000 | 2.000000 | 1.000000 | 0.100000 |
| 25% | 5.100000 | 2.800000 | 1.600000 | 0.300000 |
| 50% | 5.800000 | 3.000000 | 4.350000 | 1.300000 |
| 75% | 6.400000 | 3.300000 | 5.100000 | 1.800000 |
| max | 7.900000 | 4.400000 | 6.900000 | 2.500000 |
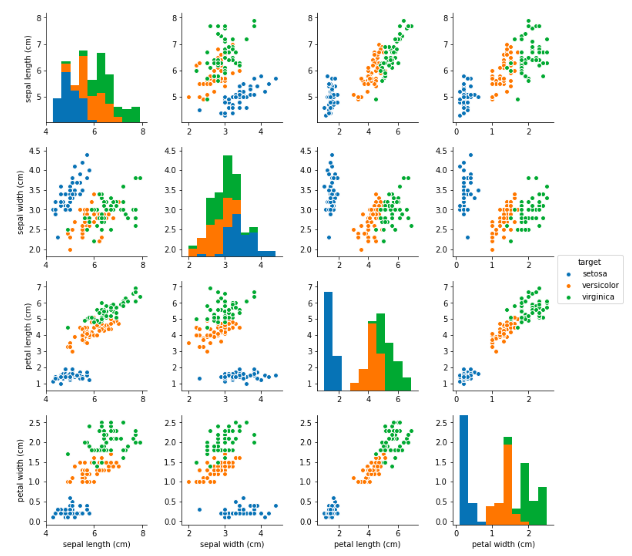
ペアプロット
ペアプロットします。各特徴量のペアごとに散布図を表示させることができます。
import seaborn as sns
# JupyterLab で実行する際は、この行を書くことで描画できるようになります。
%matplotlib inline
sns.pairplot(df, hue="target")
どの特徴量のペアで見ても同じ品種が固まっていますので、比較的分類しやすそうなデータセットだと言えそうです。
分類アルゴリズム
ここでは各分類アルゴリズムの特徴を見るために、作成したモデルの決定境界(decision boundary)を表示していきます。そのため、モデルを validation 用、test 用に分けたり、正答率の評価は行わないのでご了承ください。
X に訓練データをセットします。ここでは、特徴量はガクの長さ、花弁の長さの二つだけ使用します。y に教師データとして品種をセットします。
# import some data to play with
X = iris.data[:, [0, 2]]
y = iris.target
描画用に以下のコードを実行しておきます。scikit-learn のページより、多くを参考にさせていただいたコードです。
import numpy as np
import matplotlib.pyplot as plt
# graph common settings
h = .02 # step size in the mesh
x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
def decision_boundary(clf, X, y, ax, title):
clf.fit(X, y)
# Plot the decision boundary. For that, we will assign a color to each
# point in the mesh [x_min, x_max]x[y_min, y_max].
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
# Put the result into a color plot
Z = Z.reshape(xx.shape)
ax.pcolormesh(xx, yy, Z, cmap=plt.cm.Paired)
# Plot also the training points
ax.scatter(X[:, 0], X[:, 1], c=y, edgecolors='k', cmap=plt.cm.Paired)
# label
ax.set_title(title)
ax.set_xlabel('sepal length')
ax.set_ylabel('petal length')
教師あり学習
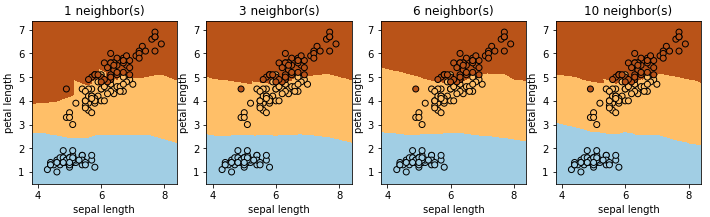
k-近傍法 (k-NN)
モデルには訓練データセットを格納するだけです。予測時は、予測したいデータポイントの近くの k 個の近傍点を確認します。その中で一番多数派のクラスを予測結果として採用します。
KNeighborsClassifierを使用します。n_neighbors で予測に使用する近傍点の数を設定します。n_neighbors = 1 の場合は決定境界が鋭角になる部分もあります。数が多くなるに従いなだらかになっていき、10 になると境界が単純になりすぎて予測性能が落ちる場合があります。
from sklearn.neighbors import KNeighborsClassifier
fig, axes = plt.subplots(1, 4, figsize=(12, 3))
for ax, n_neighbors in zip(axes, [1, 3, 6, 10]):
title = "%s neighbor(s)"% (n_neighbors)
clf = KNeighborsClassifier(n_neighbors=n_neighbors)
decision_boundary(clf, X, y, ax, title)
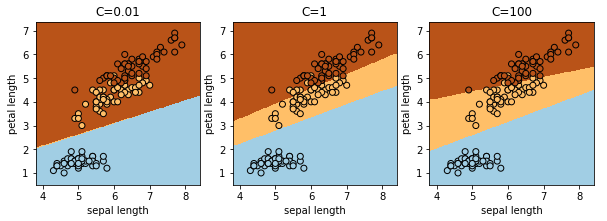
ロジスティック回帰
名前に回帰とあリますが、分類アルゴリズムです。
LogisticRegressionを使用します。決定境界は直線になります。C は正則化の度合いを調整するパラメータです。正則化は学習時にペナルティを与えることで過学習を抑える効果があります。C を大きくすると正則化が弱くなり過学習気味になりますが、小さすぎるとデータの特徴を大雑把にしか獲得できません。
ロジスティック回帰などの線形モデルは高次元(特徴量の数が多い)のデータに対して有効です。理由は高速だから、他の手法では学習できないからです。
from sklearn.linear_model import LogisticRegression
fig, axes = plt.subplots(1, 3, figsize=(10, 3))
for ax, C in zip(axes, [0.01, 1, 100]):
title = "C=%s"% (C)
clf = LogisticRegression(C=C)
decision_boundary(clf, X, y, ax, title)
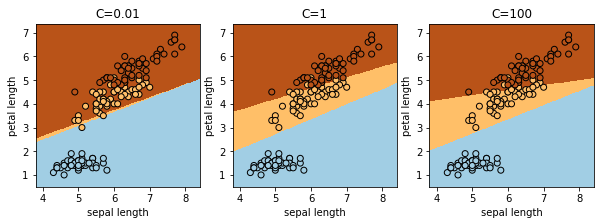
線形サポートベクタマシン
LinearSVCを使用します。線形なので、決定境界も直線になります。C はロジスティック回帰同様、正則化の度合いを調整するパラメータです。
from sklearn.svm import LinearSVC
fig, axes = plt.subplots(1, 3, figsize=(10, 3))
for ax, C in zip(axes, [0.01, 1, 100]):
title = "C=%s"% (C)
clf = LinearSVC(C=C)
decision_boundary(clf, X, y, ax, title)
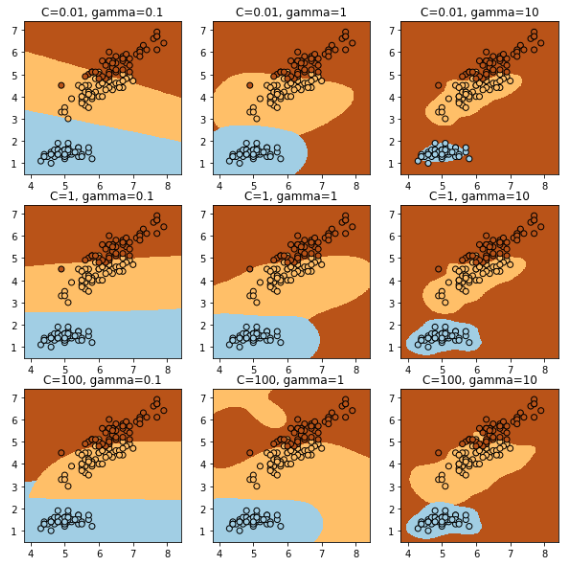
カーネル法を用いたサポートベクタマシン
SVM とも呼ばれます。線形カーネルベクタマシンと比べて、非線形な分離が可能です。
SVCを使用します。C は正則化のパラメータです、gamma は訓練データの影響が及ぶ範囲で、小さいと遠くまで、大きいと近くになります。よって、gamma が大きすぎると過学習になり、小さすぎると大雑把にしかデータの特徴を獲得できません。
パラメータの説明は RBF SVM parametersのページにも書かれています。
from sklearn.svm import SVC
fig, axes = plt.subplots(3, 3, figsize=(10, 10))
for ax_row, C in zip(axes, [0.01, 1, 100]):
for ax, gamma in zip(ax_row, [0.1, 1, 10]):
title = "C=%s, gamma=%s"% (C, gamma)
clf = SVC(C=C, gamma=gamma)
decision_boundary(clf, X, y, ax, title)
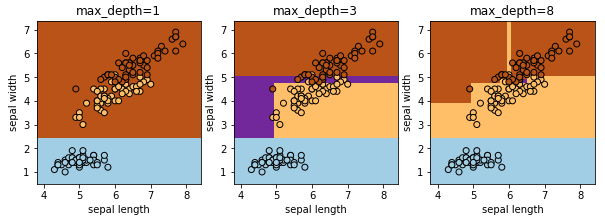
決定木
質問を通してデータを分類する手法です。あやめの場合は、花弁の長さが何センチ以上 or 未満、ガクの長さが何センチ以上 or 未満・・・と質問を繰り返すことで品種を特定していきます。
DecisionTreeRegressor を使用します。max_depth がツリーの深さで、質問数になります。多ければいいわけでもなく、訓練データに過剰適合するので過学習となります。
from sklearn.tree import DecisionTreeRegressor
fig, axes = plt.subplots(1, 3, figsize=(10, 3))
for ax, max_depth in zip(axes, [1, 3, 8]):
title = "max_depth=%s"% (max_depth)
clf = DecisionTreeRegressor(max_depth=max_depth)
decision_boundary(clf, X, y, ax, title)
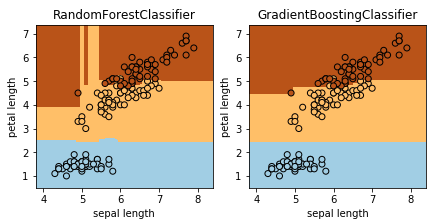
ランダムフォレスト、勾配ブースティング回帰木
ランダムフォレストは異なる決定木をたくさん作ります。全ての決定木で予測した結果からもっとも確率が高くなるラベルを正解とするものです。個々の木だと過剰適合しているかもしれないですが、多くの結果を集約することで過学習を抑制する効果があります。RandomForestClassifier を使います。
勾配ブースティング回帰木(GBDT = Gradient Boosting Decision Tree)もたくさんの決定木を作るのですが、一つ前の決定木の予測値と正解のズレを修正するように次の木を作っていくのだそうです。GradientBoostingClassifier を使います。こちらの方がランダムフォレストよりモデル構築に時間がかかったり、パラメータ設定のチューニングが大変らしいのですが、その分予測性能がよくなるのだそうです。
from sklearn.ensemble import RandomForestClassifier
from sklearn.ensemble import GradientBoostingClassifier
fig, axes = plt.subplots(1, 2, figsize=(7, 3))
clfs = [RandomForestClassifier(), GradientBoostingClassifier()]
titles = ["RandomForestClassifier", "GradientBoostingClassifier"]
for ax, clf, title in zip(axes, clfs, titles):
decision_boundary(clf, X, y, ax, title)
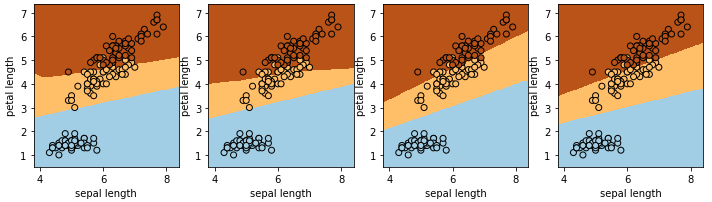
ニューラルネットワーク
scikit-learn にはニューラルネットワークのライブラリも実装されています。なお、scikit-learn は GPU に対応していない こともあり、ディープラーニングをやりたい場合は他のライブラリを選定した方がいいと思います。
前置きはさておき、MLPClassifier を使います。隠れ層 15 個で計算した結果を図示しますが、同じパラメータでも決定境界が異なっています。そうなる理由は、それぞれ異なる初期状態から学習を開始しているためです。
from sklearn.neural_network import MLPClassifier
fig, axes = plt.subplots(1, 4, figsize=(12, 3))
for ax, n in zip(axes, [15, 15, 15, 15]):
title = ""
clf = MLPClassifier(hidden_layer_sizes=[n, n])
decision_boundary(clf, X, y, ax, title)
教師なし学習
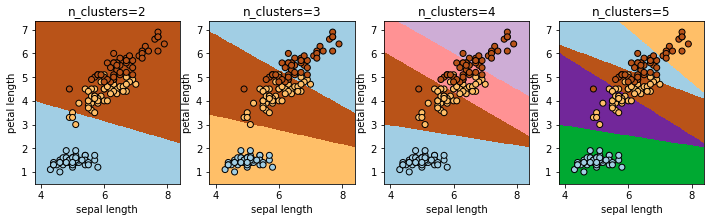
k-means
教師データなしで分類する手法です。KMeans を使います。n_clustersで何個に分類するかを指定します。
from sklearn.cluster import KMeans
fig, axes = plt.subplots(1, 4, figsize=(12, 3))
for ax, n_clusters in zip(axes, [2, 3, 4, 5]):
title = "n_clusters=%s"% (n_clusters)
clf = KMeans(n_clusters=n_clusters)
decision_boundary(clf, X, y, ax, title)
参考文献
『Python ではじめる機械学習 scikit-learn で学ぶ特徴量エンジニアリングと機械学習の基礎』
この本で各分類手法の使い方や特徴を知ることができました。体系的に学ぶことができる一冊です。そして、scikit-learn は入門用の教材としては最高だと思いました。この本は、分類手法のところ以外は読み進められていないのですが、分類手法のところを読み直すたびに新しい発見がありました。さらに読み進めていこうと思います!
実務寄りの内容です。序盤では各手法について簡潔に概要をつかむことができます。また、機械学習基盤構築やモデルのデプロイ、特徴量についての試行錯誤、データ収集や効果検証といった話題もあり、実務でどう使われているのか、役立てているのかを知るのに有用な本でした。