学び始めで頭の整理でやってます、間違っていたり何かありましたら遠慮なくご指摘お願いしますm(__)m
#回帰
回帰モデルは、連続値をとる目的変数を予測するために使用される。
このため、変数間の関係を理解したり、データのトレンドを評価したり、予報を作成するなどの形で応用されたり、科学のさまざまな問題に取り組んだりするのに適している。
（例：企業の今後数カ月間の売上を予測するなど。）
まずは、単変量の線形回帰の話から
単変量の線形回帰の目的は、単一の特徴量（説明変数x）と連続値の応答（目的変数y）との関係をモデルとして表現すること。
##最小二乗法/目的関数/最適化問題
下図で、x=200のときのyの値を知りたいとき
以下のような１次関数をひくと予測できる。
のとき、パラメータθの値を調整することで、予測精度の高いグラフを描くことができる。
したがって、パラメータθを巧みに調整することが予測精度を上げる鍵となる。
また、点(y)とグラフのy軸(f(x))が同じとき、オフセットまたは残差（回帰直線からサンプル点への予測の誤差）は0であり、一番理想的。
ただし、それはなかなか実現が難しいので、これから誤差を可能な限り小さくしていく（最小二乗法）。
そして、この最も適合する直線は回帰直線という。
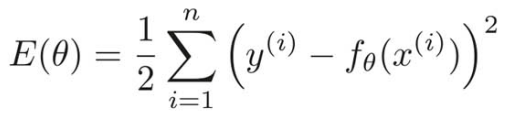*E(θ)*は**目的関数**というもので、学習データがn個あるとき、学習データごとの誤差の和を表している。
**最適化問題**では、この*E(θ)*の値が一番小さくなるような*θ*を求めるのを目的とする。
Q. 二乗しているのは何故か？
各学習データとの誤差同士の相殺を避けるため。
Q. 1/2しているのは何故か？
この1/2は、この後の計算結果を鑑みての便宜上つけた定数。
正の定数をかけても、グラフの幅が変わるだけで、最小値に影響はなく、最適化問題において、定数を勝手に付け加えても結果は同じ。
では、具体的に、どのようにして最適なθを求めることができるか？
結論は、先ほどの目的関数を微分して最小値を求める。
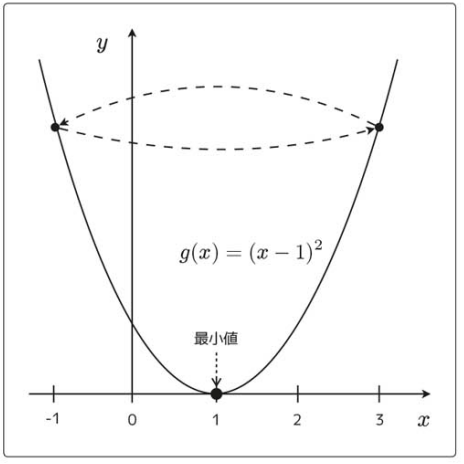
例えば、以下のような２次関数があったとする。（目的関数も２次関数）
微分すると、次のようになる。
導関数（微分した後の関数）の符号を見てみると、次のようになる。
x=3のとき、xを減らすと*g(x)は最小になる。
x=-1のとき、xを増やすとg(x)*は最小になる。
最急降下法or勾配降下法は、導関数の符号と逆の方向にずらし、最小値を見つけること。
それは次のような式で表すことができる。
Q. 「A := B」という書き方について
AをBによって定義するという意味。
新しいxを、1つ前の古いxを使って定義しているということ。
Q. η（イータ）について
ηは正の定数で、学習率を表す。
学習率の大小によって、最小値にたどり着くまでの更新回数が変わる。
学習率を変えることで、収束の速さが変わったり、収束せずに発散したりする。
具体的に、２つ例を用意する。
１つ目は、ηの値が大きすぎる場合
２つ目は、ηの値が小さすぎる場合
例１（ηの値が大きすぎる場合）：
η=1, x=3のとき、x := x-η(2x-2)なので、
となり、以下のように、3と-1をループする。
例2（ηの値が小さすぎる場合）：η=0.1, x=3のとき、
このようになり、移動量が小さくなって更新回数が増える。
勾配降下法について理解したところで、目的関数 
に当てはめてみる。
目的関数で勾配降下法を使いたい時、目的関数は
を含んでおり、
と
の２つのパラメータを持つ２変数関数であるため、普通の微分ではなく、偏微分する必要がある。
g(x)をEに置き換えて、偏微分した更新式は次のようになる。
合成関数の微分を使って、
のとき、
まず
を
で微分する。
次に、
を
で微分する。
それぞれの結果を掛け合わせて、
で微分した結果が求まる。
は
に戻しておく。
次は、
について微分する。
を
で微分すると
つまり、
を
で微分した結果は
となる。
最終的に、以下のようになる。
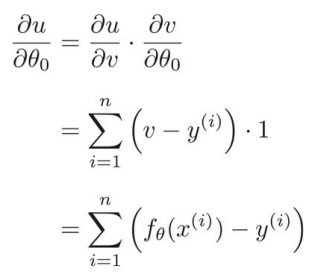
この式に従って、
と
を更新していけば、最適な１次関数
を求めることができる。
##多項式回帰/過学習
直線よりも、曲線の方が予測精度の高いグラフを導き出せることがあり、
２次関数やそれ以上の次数をもった式を使うことができる。
解きたい問題に対して、臨機応変にどのようなグラフが最も予測精度が高くなるかを考える。
次元を増やせば増やすほどフィットしやすくなるが、過学習というデメリットが起きることもある。
の式で、パラメータとして
が増えたので、目的関数を
で偏微分する。
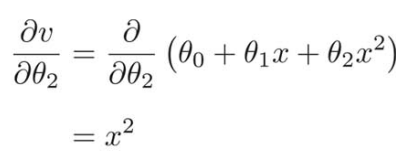
結局、パラメータの更新式は以下のようになる。パラメータが増えていっても同じように更新式を求めることができる。
このように、多項式の次数を増やした関数を使うものは、多項式回帰と呼ばれる。
##重回帰
このように、関数が複数の変数を受け取る場合、
について目的関数をそれぞれ偏微分して、パラメータを更新していく。
変数がn個ある場合、
で次のように表すことができる。
次元を調整するために、１を足す。
にならって
とすると
次にθを転置したものとxを掛けると、
となり、と同じになる。
また、ベクトルを使うと次のように表すことができる。
パラメータの更新式は、
を
で微分して、
よって、j番目のパラメータの更新式は次のようになる。ベクトルを使うことで、更新式を１つにまとめることができる。
このように、複数の変数を使ったものを**重回帰**という。
##確率的勾配降下法
普通の勾配降下法で、学習率ηが小さすぎると、更新回数が多くなり、学習率ηが大きすぎると、収束しないという欠点を学んだが、もう１つ局所解に捕まるという欠点もある。
次のような関数があった時に、
初期値によって、最小値が変わるということが以下の２つの図からわかる。
次の更新式は、普通の勾配降下法のパラメータ更新式。この式では全ての学習データの誤差を使っている。
それに対して、確率的勾配降下法では、ランダムに学習データを１つ選んで、それをパラメータの更新に使う。
この式のkはランダムに選ばれたインデックスのこと。
普通の勾配降下法で１回パラメータを更新する間に、確率的勾配降下法ではn回パラメータが更新でき、学習データをランダムに選んでその時点での勾配を使ってパラメータを更新していくから、目的関数の局所解に捕まりにくい。
ランダムに選ぶが必ず収束する。
##ミニバッチ法
学習データをランダムにm個だけ選んでパラメータを更新するやり方もある。
ランダムにm個だけ選ばれた学習データのインデックスの集合をKとおくと、次のようにパラメータを更新する（ミニバッチ法）。
##探索的データ解析
探索的データ解析は、機械学習モデルのトレーニングを行う前の、最初の重要なステップの１つ。
探索的データ解析によって、外れ値、データの分布、特徴量の間の関係を視覚的に検出するのに便利になる。
まず、散布図行列というものをつくる。
散布図行列を利用すれば、データセットの特徴量のペアに対する相関関係を１つの平面上で可視化できる。
散布図行列プロットには、seabornライブラリのpairplot関数を使用する。
（seabornはmatplotlibに基づいて統計グラフを描画するためのpythonライブラリのこと。）
続く