オミックス分野において、手元のクエリデータと類似したデータを、データベースから検索するという情報検索では、以下のような二つの考え方がある。
一つ目は、データが公共データベースに登録された時に、どのようなサンプルなのか、説明文(メタデータ)が書かれるため、メタデータに書かれている内容から、自分のデータと近しいものを探す、Semantic-basedな検索、二つ目は、計測したデータ(例: 遺伝子発現、特定の多型など)で計算した類似度を元に、近しいものを探す、Content-basedな検索である。
例えば、手元のiPS細胞の遺伝子発現データと、他所のラボが出したiPS細胞の発現データを使ってメタアナリシスをしたいとする。多くの人は、公共データベースのページにアクセスして、"iPS"と検索して、出てきたデータを使うと思われるので、無意識にSemantic-basedな検索を人力でしていることになる。一方で、データ自体をアップロードして、発現パターンが類似したサンプルをランキングするようなContent-basedなツールも、マイクロアレイ時代にはCellMontage、最近では1細胞RNA-Seq分野でCellFishing.jlといったものが出ている。特定の遺伝子が発現したサンプルだけを取ってくるというのも、中身を見て似ているか判断しているのでContent-basedに該当する(RefExなど)。
これら二つのアプローチには、おそらく各々メリット、デメリットがあるだろう。例えば、同じ細胞とメタデータに書かれていたとしても、メタデータは所詮人間が書いたものなので、記述の丁寧さや、入力ミスといった間違いがあるかもしれない。また、その研究者達が把握していない多様性がサンプル間にあるかもしれない。かといって、データの計測値こそ正義というわけでも無く、多くのオミックスデータはノイジーなので、実は低次元空間ではかなり近いデータ同士だとしても、ノイズに埋もれて気づいていないだけの可能性もある。そのため、どっちのアプローチが良いのかはよくわからないところだが、自分としては、参考になるデータはあればあるほど賢くなるはずだし、どんどんモデルに取り込んでいけば良いという考えなので、両方使ったらどうなるのかを調べたかった。
しかしながら、Content-basedの方はともかく、Semantic-basedな類似度というのは、人間が書いた文章を解析する自然言語処理を伴うので、これまでは敷居が高かったのだが、最近BioconductorでOnassisというパッケージを見つけて、結構便利そうだったので、今回試してみた。なお、rJavaを使う関係で、インストールはかなり難しいので、以下にインストールのポイントだけをまとめる。
インストールのポイント
- Javaのバージョンを1.8以上にする(Oracle JDKであれ、OpenJDKであれ)
- R CMD javareconfで、RにJavaの位置を覚えさせる
- *BiocManager::install("Onassis")*を実行
- もしインストール中に00LOCKを消せみたいな警告が出たら削除してインストールし直す
- Macの場合は、Xcodeが正常にインストールされており、かつxcode-select --installでcommand line developer toolsもインストールされている必要あり
Semantic Similarityの計算
以下、Onassisを使って、サンプル間のSemantic Similarityを計算する。詳細はOnassisのvignetteを参照して欲しいが、ここでやってる事を簡単に説明すると、細胞、組織、疾患などのオントロジーは、語彙が階層構造になっているが、この木構造を考慮した、語彙間の類似度をSemantic Similarityといい、Onassisは11種類のSemantic Similarityを実装している(cf. Onassis::listSimilarities())。これとは別に、サンプルごとのメタデータを取得しておき、先ほどのオントロジーで定義してある語彙がメタデータに含まれているかを調べることで、サンプル間のSemantic Similarityも計算する。
OBOかOWL形式になっているオントロジーならなんでも取り込めるので、拡張性が高い。また、複数のオントロジーをマージして、Semantic Similarityを計算したり、アノテーションをするところで、細かいオプションを設定できたりする。内部でOracleのConceptMapperというツールを使っているらしい。
連続値としてのサンプル間のSemantic Similarityが本当は欲しかったのだが、collapse関数の中でしか計算されなそうだったので、ここではcollapse後に、同じクラスターか否かをクラスタリングで判定された結果を離散的な類似度として扱う。
library("Onassis")
library("GEOmetadb")
library("nnTensor")
library("uwot")
library("RColorBrewer")
# ChIPデータのメタデータ
h3k27ac_chip <- readRDS(system.file('extdata', 'vignette_data', 'h3k27ac_metadata.rds',
package='Onassis'))
# OBOでアノテーション
obo <- system.file('extdata', 'sample.cs.obo', package='OnassisJavaLibs')
cell_annotations <- annotate(h3k27ac_chip, 'OBO', obo, FindAllMatches='YES')
# Cell, Tissueに説明文があるものだけをフィルタリング
cell_entities <- entities(cell_annotations) # 323 × 5
filtered_cells <- filterconcepts(cell_annotations, c('cell', 'tissue')) # 60 × 5
# Semantic Similarity
filtered_cells <- sim(filtered_cells)
# 階層的クラスタリングによる、クラスタラベルの作成
simcluster <- Onassis::collapse(filtered_cells, 0.9)
Content Similarityの計算
Content Similarityの方は簡単で、ここではOnassisが既に用意してあるChIP-Seqのデータをそのまま使う。
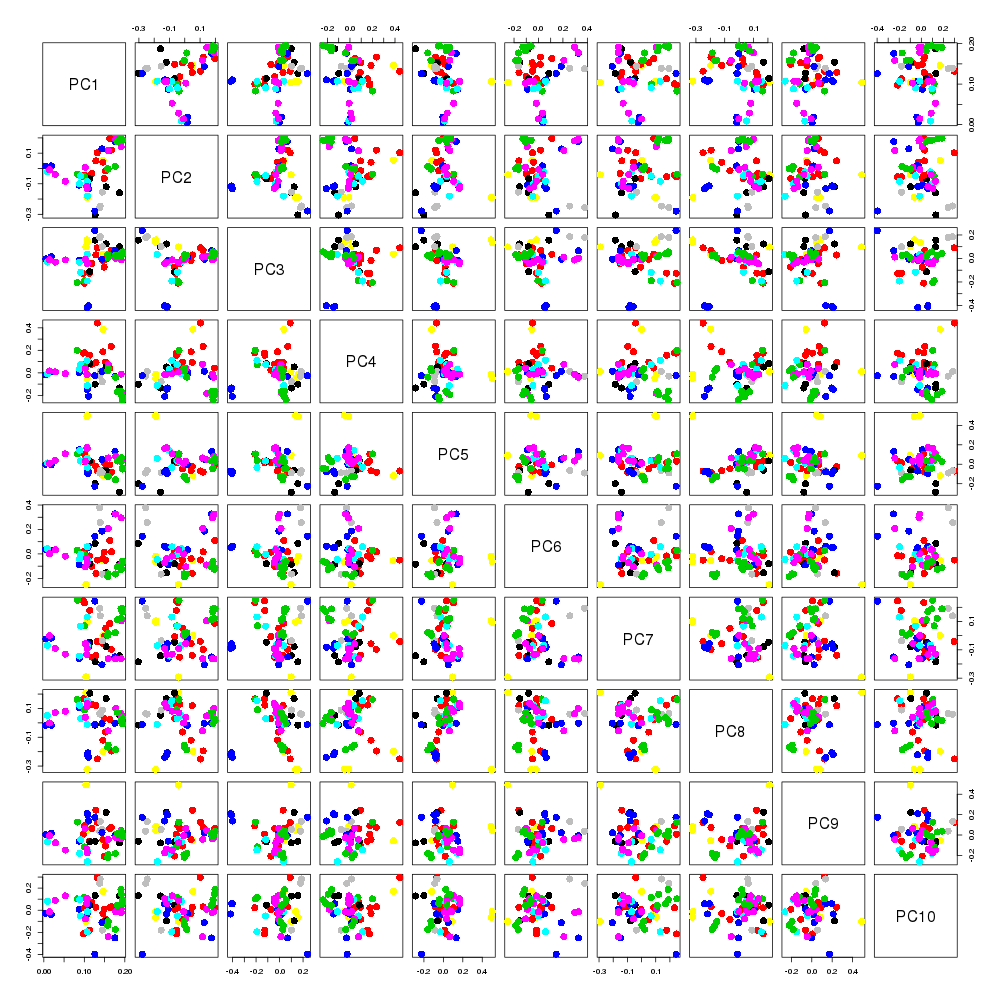
試しに、PCAをしてみたが、あまりはっきりとした構造が見えづらそうである(下の図のラベルは上のsimclusterを利用)。
score_matrix <- readRDS(system.file('extdata', 'vignette_data', 'score_matrix.rds',
package='Onassis'))
out.pca <- prcomp(log10(score_matrix + 1))
png(file="plot/PCA.png", width=1000, height=1000)
pairs(out.pca$rotation[,1:10], col=simcluster@entities$cluster, pch=16, cex=2)
dev.off()
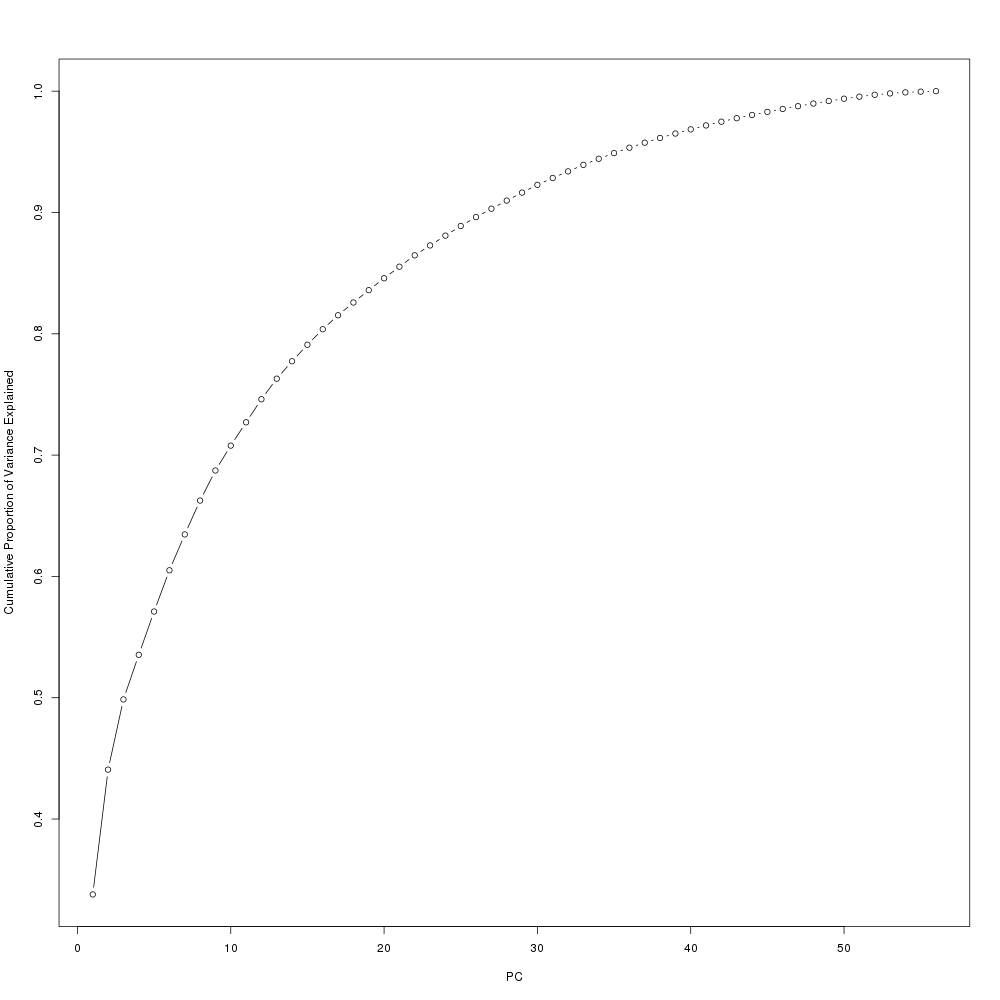
png(file="plot/ExpVar.png", width=1000, height=1000)
expvariance <- out.pca$sdev^2/sum(out.pca$sdev^2)
plot(cumsum(expvariance), xlab="PC", ylab="Cumulative Proportion of Variance Explained", type="b")
dev.off()
行列同時分解、可視化
上で、Semantic SimilarityとContent Similarityが計算できたので、これらを違う重みでマージして、解析結果がどのように変化していくのかを調べた。なおここでは、自分が作った、nnTensorパッケージ内で実装したjNMF関数を使って、二つの行列をお互いに関連づけさせながら同時に分解するjoint NMFという手法を使った。この手法は、今年出たLIGERという1細胞オミックスのバッチエフェクト除去の手法や、scTGIFという自分が作ったパッケージのエンジン部分にもなっている。この手法で得られたサンプルごとの特徴量を、最後UMAPで次元圧縮して可視化を行った。
commonid <- intersect(filtered_cells@entities$sample_id, colnames(score_matrix))
target <- sapply(commonid, function(x){
which(simcluster@entities$sample_id == x)})
cluster <- simcluster@entities$cluster[target]
S_Sim <- outer(cluster, cluster, "==")
S_Sim[which(S_Sim == TRUE)] <- 1
S_Sim[which(S_Sim == FALSE)] <- 0
rownames(S_Sim) <- commonid
colnames(S_Sim) <- commonid
C_Sim <- t(score_matrix[, commonid])
# jNMF
set.seed(1234)
out_jnmf_10_0 <- jNMF(X=list(S_Sim, C_Sim), J=20, w=c(10, 0))
set.seed(1234)
out_jnmf_9_1 <- jNMF(X=list(S_Sim, C_Sim), J=20, w=c(9, 1))
set.seed(1234)
out_jnmf_8_2 <- jNMF(X=list(S_Sim, C_Sim), J=20, w=c(8, 2))
set.seed(1234)
out_jnmf_7_3 <- jNMF(X=list(S_Sim, C_Sim), J=20, w=c(7, 3))
set.seed(1234)
out_jnmf_6_4 <- jNMF(X=list(S_Sim, C_Sim), J=20, w=c(6, 4))
set.seed(1234)
out_jnmf_5_5 <- jNMF(X=list(S_Sim, C_Sim), J=20, w=c(5, 5))
set.seed(1234)
out_jnmf_4_6 <- jNMF(X=list(S_Sim, C_Sim), J=20, w=c(4, 6))
set.seed(1234)
out_jnmf_3_7 <- jNMF(X=list(S_Sim, C_Sim), J=20, w=c(3, 7))
set.seed(1234)
out_jnmf_2_8 <- jNMF(X=list(S_Sim, C_Sim), J=20, w=c(2, 8))
set.seed(1234)
out_jnmf_1_9 <- jNMF(X=list(S_Sim, C_Sim), J=20, w=c(1, 9))
set.seed(1234)
out_jnmf_0_10 <- jNMF(X=list(S_Sim, C_Sim), J=20, w=c(0, 10))
# UMAP
set.seed(1234)
out_umap_10_0 <- umap(out_jnmf_10_0$W, n_neighbors=5, init="random")
set.seed(1234)
out_umap_9_1 <- umap(out_jnmf_9_1$W, n_neighbors=5, init="random")
set.seed(1234)
out_umap_8_2 <- umap(out_jnmf_8_2$W, n_neighbors=5, init="random")
set.seed(1234)
out_umap_7_3 <- umap(out_jnmf_7_3$W, n_neighbors=5, init="random")
set.seed(1234)
out_umap_6_4 <- umap(out_jnmf_6_4$W, n_neighbors=5, init="random")
set.seed(1234)
out_umap_5_5 <- umap(out_jnmf_5_5$W, n_neighbors=5, init="random")
set.seed(1234)
out_umap_4_6 <- umap(out_jnmf_4_6$W, n_neighbors=5, init="random")
set.seed(1234)
out_umap_3_7 <- umap(out_jnmf_3_7$W, n_neighbors=5, init="random")
set.seed(1234)
out_umap_2_8 <- umap(out_jnmf_2_8$W, n_neighbors=5, init="random")
set.seed(1234)
out_umap_1_9 <- umap(out_jnmf_1_9$W, n_neighbors=5, init="random")
set.seed(1234)
out_umap_0_10 <- umap(out_jnmf_0_10$W, n_neighbors=5, init="random")
# plot
mycol <- c(brewer.pal(9, "Set1"), "#000000")
png(file="plot/UMAP.png", width=1400, height=1100)
par(mfrow=c(3,4))
plot(out_umap_10_0, col=mycol[cluster], pch=16, cex=2, xlab="Dim1", ylab="Dim2", main="10 : 0")
plot(out_umap_9_1, col=mycol[cluster], pch=16, cex=2, xlab="Dim1", ylab="Dim2", main="9 : 1")
plot(out_umap_8_2, col=mycol[cluster], pch=16, cex=2, xlab="Dim1", ylab="Dim2", main="8 : 3")
plot(out_umap_7_3, col=mycol[cluster], pch=16, cex=2, xlab="Dim1", ylab="Dim2", main="7 : 3")
plot(out_umap_6_4, col=mycol[cluster], pch=16, cex=2, xlab="Dim1", ylab="Dim2", main="6 : 4")
plot(out_umap_5_5, col=mycol[cluster], pch=16, cex=2, xlab="Dim1", ylab="Dim2", main="5 : 5")
plot(out_umap_4_6, col=mycol[cluster], pch=16, cex=2, xlab="Dim1", ylab="Dim2", main="4 : 6")
plot(out_umap_3_7, col=mycol[cluster], pch=16, cex=2, xlab="Dim1", ylab="Dim2", main="3 : 7")
plot(out_umap_2_8, col=mycol[cluster], pch=16, cex=2, xlab="Dim1", ylab="Dim2", main="2 : 8")
plot(out_umap_1_9, col=mycol[cluster], pch=16, cex=2, xlab="Dim1", ylab="Dim2", main="1 : 9")
plot(out_umap_0_10, col=mycol[cluster], pch=16, cex=2, xlab="Dim1", ylab="Dim2", main="0 : 10")
dev.off()
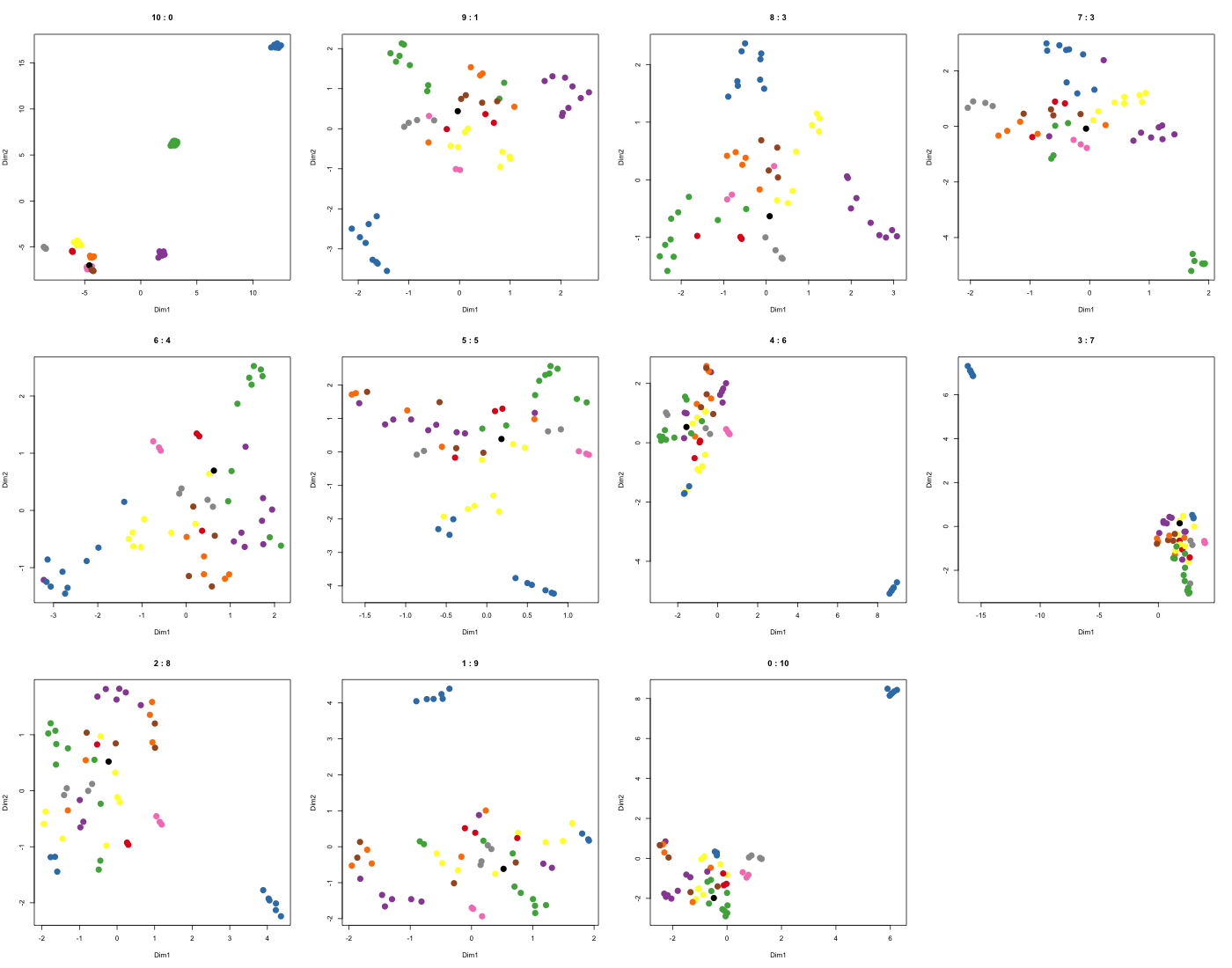
Content-basedな類似度と、Semantic-basedな類似度をマージする際に、0:10、1:9、...、10:0という風に、異なる重みで統合したところ、結果は以下のようになった。
まず、10:0ははっきりとクラスターが分かれているが、Semantic-basedな類似度しか使っておらず、かつクラスターラベルで色分けしているので、これはある意味当たり前である。一方、0:10は完全にオミックスデータだけを使ったContent-basedなやり方になるわけだが、青のクラスターが大きく離れているが、他のクラスターはごちゃついている。これが5:5くらいになると、ラベルの手助けにより、ごちゃついていたクラスターの内部がもう少しわかるようになる。行列分解は、線形な射影をしているだけなので、高次元空間のどこかに、そのクラスターだけを分離する軸があり、完全な教師なしではノイズに埋もれてわからないが、ちょっとラベルの情報も使えば、そういう軸が見つかる事を示唆している。PCAもICAもNMFも、外れ値の影響を受けやすいので、それを教師無し学習における過学習と捉えるならば、このちょっと別の目的関数も足すというのは、正則化をしているとも言える(cf. グラフ正則化)。
さて、ではこれらを結局何対何で混ぜるとちょうどいいのか?行列分解 = 次元圧縮 = 教師なし学習と捉えると、パラメーターの値の選び方は、主観的な話しになりやすいが(分散の8割を説明するPCを使うとか)、自分の知る限り、二つの良さそうな考え方がある。一つ目は、とにかく使ったデータをフェアに統合するやり方である。行列の同時分解では、ダイナミックレンジが大きかったり、サイズが大きい行列の方が最適化の結果に影響を与えやすいので、そのままの値を使っても、そもそも複数の行列をフェアに扱えていない。そのため、各々の行列の最大固有値で割る(cf. graph-PCA、MFA)、またはフロベニウスノルムの2乗で割る(cf. JIVE、siNMF)など正規化をして、できるだけフェアに複数の行列を扱おうというものである。
二つ目は、教師あり学習に話しをシフトする、つまり計算した特徴量を元に何か予測するという問題に変更して、クロスバリデーション(CV)で重みを決めるやり方である(cf. CP-WOPT、今回の場合、メタデータでもChIP-Seqの値も無い、第三の尺度(例: 病気のなりやすさとか)を用意する必要があって、めんどくさくてやらなかったが)。そもそも、こういった重みは、目的関数を重みで微分して0になるところを探すみたいな事をやっても、大きい値をとる方の関数を1、小さい方は0という重みになるだけなので、データはマージしない方が良いという結論になってしまう(cf. 多目的最適化、パレート解)。一方で、CVがやってることは、一つの目的関数の最適化ではなく、真のデータとの誤差を最小化すべく、データを分割して、複数の最適化問題を解いて、平均的に良いパラメーターを探すため、上記のような問題にはならず、実際にデータをマージした方が、解析精度が上がったという報告は幾つもある(cf. マルチモーダル学習、マルチタスク学習)。
まとめ
途中から、自分のツールの宣伝にもなってしまったが、今回紹介しきれていないOnassisの機能がvignetteに書かれていて、ConceptMapperの細かい設定や、複数のオントロジー をマージしてSementic Similarityを使うやり方、collapseで分けたクラスター間での仮説検定(cf. Onassis::compare())などもできるらしい。Onassisでこれまで手に入りづらかった、Semantic Similarityが手に入りやすくなったので、今後の解析の幅が広がりそう。