はじめに
私はBrainf**kerなんですが、今年(2018年)書くネタがなかったので、最近ゴルフ場で最短を更新したWhiteSpaceのQuineについて書こうと思います。
※2022/11/30追記: その後330Bに大幅更新しました。そのうち書くと思います
WhiteSpaceについて
WhiteSpaceについては、アドベントカレンダー前日のWhiteSpaceアセンブラ・逆アセンブラの紹介をご参照ください。
コードについても、そちらのツールでの書式に合わせて記載します。
WhiteSpaceでのQuine
Quineとは、色々な応用がありますが、基本は「プログラムコードと同じ内容を出力するプログラム」のことです。
言語によって色々戦略があるわけですが、WhiteSpaceの場合だと出力内容が空白・タブ・改行の3種類の文字だけなので ( 別の文字を混ぜても構わないんですが )、次のような方針が素直と言えます。
- 空白・タブ・改行を 0,1,2 に対応付け ( 順番は今後検討 )、文字列を3進法で扱う。
- 記憶している数値を3進法解釈し、対応する文字を出力するコードを組む。
→ この部分を A とする。 - 記憶している数値と同じデータを作り出すコードを出力する ( 或いは A で処理するデータに追加する ) コードを組む。
→ この部分を B とする。 - B+A のコードを数値化し、その数値データを作るコードを組む。
→ この部分を C とする。 - C+B+A と3つを連結したコードがQuineとなる。
このようにすることで、
- Cの部分が実行され、B+Aに対応するデータが作り出され記憶される。
- Bの部分が実行され、記憶されたデータを作り出すコードに対応する文字列 ( つまりCと同一内容 ) が出力される。
あるいは、後に出力されるよう、データが追加で記憶される。 - Aの部分が実行され、記憶されたデータを文字列化したもの ( B+Aと同一内容 ) が出力される。
※ B で出力を行わなかった場合は、記憶されたデータを文字列化することで C+B+A と同一内容になっている想定。
というように、うまく自分自身を出力してくれるだろう、という目論見です。
最短の更新
オリジナル
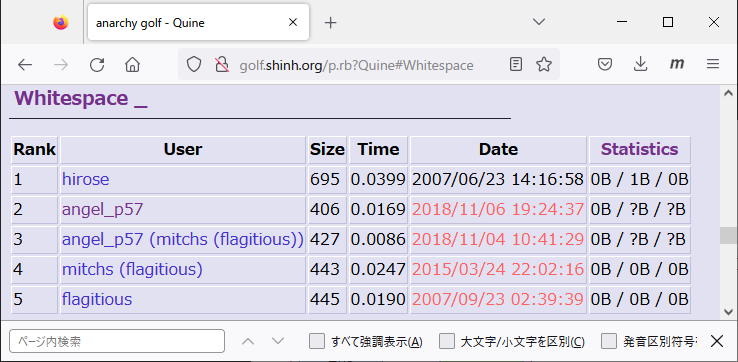
さて、WhiteSpaceのQuineの短コードには先駆者がおり、その方の443文字のコードを参考にしました。
上記A,B,Cに対応する処理は次のようになっています。
- A: スタックにある数値を3進数解釈し、0→空白(32)、1→タブ(9)、2→改行(10)の文字コードに変換し、下位の桁から1文字ずつ出力する。
- B: スタックにある数値のコピーを2進→3進変換し、元の数値の下位の桁に付け足す。ついでに27倍する。
- C: 改行+B+A の部分に対応する数値をスタックに積む。
先にBですが、上記コードのDisassemble:の内容の2行目~20行目が該当します。最後に27倍しているのは、C の push 命令が、sss+(2進化した数値) と、符号の桁も併せて空白3連続になっているためです。
ついでに、C の「改行+B+A」の改行とは、push命令の数値の終わりを示す改行に対応します。
問題は、Aの3進数としての桁 d=0~2 から各文字コードcへの変換のロジックです。
負の除数による剰余というのが見慣れないかも知れませんが、この場合結果も負になるため、d=0 の時の c=32 に比べ、タブ・改行という小さな文字コードも同じ式で計算できるようになっています。
$$
c=mod(-23d,-24)+32
$$
なお、Aで3進数の桁がなくなった場合 ( divの結果が0になった場合 )、jzero で B の先頭付近まで飛んでて何事かと思うかも知れませんが、もうスタックに十分なデータは残っていないため処理が継続できなくて打ち切られます。
WhiteSpaceのゴルフの場合、終了を end命令 ( nnn ) で書くことは滅多になくて、なんらかのスタック不足等を引き起こして打ち切らせるのが常套手段になっています。
第一の改善
最初に投稿したのは、上記オリジナルの改善版427文字でした。
どこに着目したかと言うと、Aの処理の中での、文字コード変換ロジックです。( 以下に再掲します )
$$
c=mod(-23d,-24)+32
$$
23,24,32 がそれぞれ5bit,5bit,6bitと比較的大きな数字になっています。
この数字の大きさ(bit数)というのは、そのままpush命令でスタックに積む時のコードの長さに直結しますから、より小さい数字を使って同じ結果が生み出せれば、それだけで短縮になるのです。
ということで考えたのが次の変換式です。
$$
c=mod(d-1,24)+9
$$
つまり、d=1~2の時modで大きなマイナスを作って32から引き下げる代わりに、d=0の時だけmodで大きな数を作るという発想です。単純ですが、これだけでコード部分が6bit減り、それを数値化した部分も(3進数換算なので約1.5倍で)10bit程度、合計16文字の短縮に結び付いています。
ところで、空白・タブ・改行に当たり前のように0,1,2を割り当てていましたが、これにも理由があります。
まず、タブ・改行は文字コードが9,10と連続してますから、0,1あるいは1,2のように連続した数値をあてないと文字コード変換が大変になります。
加えて、処理Bで2進→3進変換するとき、2進の桁0,1がそのまま、コード上の0,1を示す空白・タブに割り当たった方が余分な処理がなくなります。
というところから、0,1,2の割り当ては他に考え辛いのです。
なお、3進数としての桁数を別途持っておくことはできませんから、最上位の桁が0になるような選び方だと別の意味で困ってしまいます。最上位の桁はコードの最後、jump命令のラベルの終端である改行ですから、改行に2を割り当てるのはセーフです。
最短コード
上記改善でも、結構文字数のインパクトはありますから、一時は満足しかけたのですが、あることに気付いて更なる短縮を試みました。
結果、406文字の最短コードを達成することができました。
※このアセンブリコードはgithubにあげてあります。
それは処理Bの2進→3進変換での、×3 のタイミングです。
元々、$x \rightarrow 3x+d$ のような計算を繰り返していましたが、どうせ後で27倍するので、$x \rightarrow 3(x+d)$ でもいいじゃないか、と気付いたのです。結果が3倍になりますから、後で掛ける数が9になって、その分コード上の数字の桁数が減ります。
とは言え、こちらでは最初にCで用意する数を3倍に増やさなければいけませんから、相殺されて効果は1文字程度しかありません。が、ここで後からの×9をまるっと消す方法を思いついたのです。
それは、処理Aで0を活用しループ回数を水増しする方法です。
処理Aのループは、divにより残った数が0になると処理を抜けるのですが、最初から0が入ってきた場合でも最低1回はループを回ります。
つまり、スタックに余分に0を2個積んでおき、本命の数以外に2個の0、都合3個分をAで処理させることで、本命の数だけに比べての×9と同等の効果を狙ったわけです。
ただそうすると、処理Aをjzeroで抜ける時に処理Bの先頭に回すわけには行きません。
かと言って単純にAの先頭に飛ぶだけだと、処理が終わった0がいつまでも消えずに無限ループを引き起こしてしまいます。
そこで、処理Bの中間 ( コードのDisassemble:の結果16,17行目 ) にjzeroを挟み、余る0を吸収させることにしました。これは処理Bを抜けて処理Aへ移る判断も兼ねられて一石二鳥です。
後は、処理Bの中で適宜dupで計算結果を多くコピーしておくことで、余分な0を作っておきます。
※処理Bが終わらないうちは追加したpopで削除されるので、余分に作っても問題にならない。
ちなみに、処理Bが元々 jneg で「負ならループ継続」としていたところを、jzero で「0ならループ終了」に替えているわけでもあり、負を作り出すための×(-1)の削減にもなっています。ここも大きい所です。
ということで21文字の削減につながりました。
終わりに
WhiteSpace は、分岐命令に癖があったり、スタックの使い方で命令数が変わったりして、思わぬところで文字数を縮めることができます。が、それなりに素直に組むだけでも短いコードが作れます。
ゴルフの題材として、結構とっつき易いのではないでしょうか。