電子署名EdDSA(ed25519)の数的構造

はじめに

以前の電子署名DSA/ECDSAの数的構造に引き続き、EdDSAについてもまとめられないかと記事にしてみました。

EdDSAの概要

EdDSAとは?

EdDSAとは、暗号研究者であるDJB氏 ( qmailやdjbdns等のミドルウェア、sendmail,BIND,IPv6等の問題への指摘でも有名ですが ) 等が開発した、比較的新しい署名方式です。
名前のedは、楕円曲線の一種であるエドワーズ曲線 ( 正確にはツイスト化したエドワーズ曲線 ) から、25519というのは活用しているCurve25519 ( mod $2^{255}-19$ での楕円曲線の1つ ) から来ています。
基本的にはDJB氏等の論文を読めばそれで済むのですが、以下では前の記事のDSA/ECDSAとの対比に主眼を置いて説明していきたいと思います。

EdDSAの特徴

新しい方式の電子署名ということで、もちろん処理の高速化や堅牢性等の考慮が含まれているのですが、その辺はオリジナルの論文をご覧いただくとして、特徴を挙げてみます。

• Curve25519という楕円曲線上の群構造を利用した、楕円曲線暗号の一種であること。
• シュノア署名の応用であり、DSA/ECDSAと同様、有限群に対する離散対数問題の困難さを根拠とした署名方式であること。
• DSA/ECDSAの短所への対策が各種盛り込まれていること。
• バッチ処理 ( 複数の署名の一括検証 ) に対応していること。

EdDSAの数的構造

前提

以下では、DSA/ECDSAの時と同じように、以下が用意されていることを前提とします。

• 有限群$(G,\circ,\epsilon)$
• $G$の要素$\gamma$および素数 q ただし、$\gamma^q=\epsilon$
• 3つの関数 $f_x: K\rightarrow GF(q), f_k:K\times M\rightarrow GF(q), f_z:G\times G\times M\rightarrow GF(q)$

この$G$というのが楕円曲線Curve25519に基づく有限群、$\gamma, q$というのは固定された$G$上の要素とその位数となっています。ただし、EdDSAの原理自体は特定の楕円曲線でなくとも汎用的に使えるものです。
なお、DSA/ECDSAの時の$f_p$に相当する関数はありません。代わりに$f_x,f_k$の2つが追加されています ( これはこの記事上で独自につけた関数名であり、オリジナルでこういう表現はしていません )。ここの$K$は、鍵ペア生成で出てくる秘密情報$c$の所属する何かしらの集合と考えて下さい。$M$は例によってメッセージの所属する何かしらの集合です。

EdDSAの各処理

鍵ペア生成

DSA/ECDSAの署名鍵・検証鍵に相当する$x,\chi$がEdDSAの場合にもあるのですが、その元になる秘密情報$c$というのがあります。$c$からのそれぞれの生成は次のようになります。

• $x=f_x(c)$
• $\chi=\gamma^x$

なお、関数$f_x$は、$c$のハッシュ値の一部ビットを削除・追加した2進数を生成するものです。要は乱数をそのまま$x$にするのではなく、元の秘密情報にハッシュ処理を通していることが肝です。この$c$は署名の時にも使います。

署名作成

メッセージ$m$に対し、鍵ペア生成の時に登場した秘密情報$c$を元に一時的な秘密情報$k$を生成し、そこから計算した$(\rho,s)$の組を署名とします。

• $k=f_k(c,m)$
• $\rho=\gamma^k$
• $s=k+f_z(\rho,\chi,m)x$

ここで、関数$f_k$は、$c$のハッシュ値の半分のビットと、$m$をつなぎ合せて更にハッシュ値を取ったものです。$f_z$は、$\rho,\chi,m$をつなぎ合せてハッシュ値を取るものです。
いや「つなぎ合せて」ってなんやねん? というのは、何かしらデータをビット列表現して、それらをつなぎ合せたビット列を作るような処理だと思ってください。つまり、細かいことは気にすんなってことです。

署名検証

メッセージ$m$と署名$(\rho,s)$、検証鍵$\chi$を元に以下の比較を行います。

• $\gamma^{8s}=\rho^8\circ\chi^{8f_z(\rho,\chi,m)}$

この等式が成立していれば検証成功、さもなくば検証失敗ということです。

この指数に出てくる8って何の意味があるの? というと、実は良く分かっていません ( 誰かご教示頂けると嬉しいです )。が、この 8 を抜いた $\gamma^s=\rho\circ\chi^{f_z(\rho,\chi,m)}$ という等式でも問題はありません。

この検証方法が上手くいくのは、署名データの$s$が$s=k+f_z(\rho,\chi,m)x$と計算されているところから容易に確認できます。

$$
\begin{eqnarray}
&~&s=k+f_z(\rho,\chi,m)x \\
&\Rightarrow& 8s=8k+8f_z(\rho,\chi,m)x \\
&\Rightarrow& \gamma^{8s}=\gamma^{8k+8f_z(\rho,\chi,m)x} \\
&\Leftrightarrow& \gamma^{8s}=\gamma^{8k}\circ(\gamma^{x})^{8f_z(\rho,\chi,m)} \\
&\Leftrightarrow& \gamma^{8s}=\rho^8\circ\chi^{8f_z(\rho,\chi,m)} \\
\end{eqnarray}
$$

DSA/ECDSAとEdDSAの比較

同じ離散対数問題をベースにしている以上、DSA/ECDSAとEdDSAでは似ている点が多いですが、色々違う点もあります。

• 署名鍵のランダム性確保
  離散対数問題の困難さを利用しているわけですが、$\omega=\gamma^z$となる既知の$(\omega,z)$の組があると、そこを攻撃者に利用されることになります。だからと言って、$x$が既知の$z$と一致するかどうかを逐一調べるというのは現実的ではありません。
  ということから、EdDSAでは秘密情報$c$を用意し、ハッシュを通して$x$を生成することでランダム性を確保しています。
• 一時的な秘密情報$k$のランダム性確保
  DSA/ECDSAでは$k$を単なる乱数として生成していましたが、$k$のパターンが読まれる、或いは$k$の使い回しがあるようだと、そこから署名鍵$x$が漏洩してしまうという問題がありました。そこで、EdDSAではメッセージ$m$と、秘密情報$c$をハッシュに通して$k$を生成することで、$k$にもランダム性を確保しています。
• 簡潔な署名作成・検証
  DSA/ECDSAでは、署名作成時に$k$での除算、署名検証時に$s$での除算という、いずれも$GF(q)$での逆演算がありました。この逆演算の裏では、拡張ユークリッドの互除法に伴う巨大整数の除算・剰余算が多数実行されますから、それなりに重い処理になります。EdDSAではシュノア署名ベースの処理にすることで、この逆演算を取り除いています。
  このことに伴い、DSA/ECDSAにあった、$r=f_p(\gamma^k)$と$f_p$を通すことで、群の要素$\gamma^k$よりも容量を縮小した$r$を署名データとするという仕組みもなくなっていますが、そもそも楕円曲線を使う方式ではそれほど恩恵が出るわけではありませんから、さほどのデメリットにはならないと推測できます。
• ハッシュ衝突への耐性
  この点もシュノア署名から受け継いでいる点ですが、関数$f_z$でメッセージ$m$単独ではなく、他のデータも混ぜてハッシュを計算することで、ハッシュ衝突への耐性を確保しています。というのは、もし同一のハッシュ値を生む2つの既知のメッセージがあった場合、DSA/ECDSAで生成された署名はどちらのメッセージとの検証も通ってしまいますが、EdDSAではそうなりませんから。

バッチ処理による署名の一括検証

さて、EdDSAの特性として、複数の署名を一括で検証する手法が使えることも論文で挙げられています。

単体での検証が次の計算であるのに対し、

• $\gamma^{8s}=\rho^8\circ\chi^{8f_z(\rho,\chi,m)}$

複数のメッセージ$m_i$、検証鍵$\chi_i$、署名$(\rho_i,s_i)$ に対して、乱数列$z_i$を用意して次の計算を行います。なお、$\prod$に関しては$\prod \omega_i=\omega_1\circ\omega_2\circ\cdots$という複数要素の$\circ$演算と解釈してください。

• $\gamma^{\sum s_i z_i}=\prod \rho_i ^{z_i} \circ\prod \chi_i^{z_i f_z(\rho_i,\chi_i,m_i)}$

こうすることで、$\gamma^s$という群の要素の演算を1つにまとめることができます。
更に、もし同一の鍵を持つ相手の署名である場合、つまり$\chi_i$が共通の$\chi$だとすると、もっとまとめることができます。

• $\gamma^{\sum s_i z_i}=\prod \rho_i ^{z_i} \circ\chi^{\sum z_i f_z(\rho_i,\chi,m_i)}$

$z_i$に乱数列をあてていることから、これらの等式が成立するのであれば、個々の署名検証の等式も成立することが分かります。もちろん、本当は署名が不当であっても偶然検証が通ってしまう可能性もあるのですが、それは極僅かなので、実用上は無視できます。
逆にもし等式が成立しない場合は、いずれかの署名が不当ということです。ただ、どの署名が不当なのかまでは分かりませんから、改めて個々の署名を検証していくことになります。

EdDSAで利用している楕円曲線

楕円曲線の表現形式

ECDSAの説明でも楕円曲線$y^2=x^3+ax+b$というのが出てきましたが、実は楕円曲線にも色々な形式があります。

• ワイエルシュトラス型
  $y^2=x^3+ax+b$という形式で表現されるものです。
• モンゴメリ型
  $By^2=x^3+Ax^2+x$という形式で表現されるもので、必ず原点を通ります。

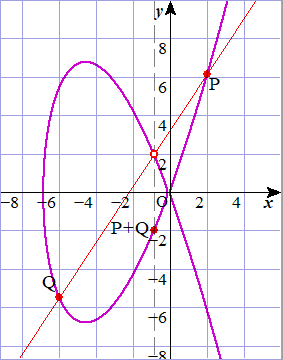
なお、モンゴメリ型は適当な変数変換を行うことで、ワイエルシュトラス型に変形することができます。また両者とも、無限遠点という特殊な点を加えることで、群としての演算を定義することができます。それは、楕円曲線上の異なる点P,Qに対し、直線PQと曲線の交点のy座標を符号反転した点をP+Qとするというものです ( この + というのは、上で$\circ$と表現していた演算のことです )。次の図は、モンゴメリ型$y^2=x^3+7x^2+x$における演算を可視化したものです。

なお、無限遠点はこの演算の単位元として働きますよ、とか、P,Qが一致する場合は直線PQではなくてPにおける曲線の接線としますよ、とか、色々あるのですが細かいところは割愛します。

ツイスト化されたエドワーズ曲線

というところで、今度はEdDSAで使われているツイスト化されたエドワーズ曲線です。これは次のような形式をしています。

• $ax^2+y^2=1+dx^2 y^2$

$x^2$の係数として$a$が付いているのが「ツイスト化された」であり、素の「エドワーズ曲線」は$a=1$という特殊なケースに相当します。

上で挙げたワイエルシュトラス型やモンゴメリ型とは似ても似つきません。が、これも楕円曲線の一形式であり、次の変換によってモンゴメリ型に変形することができます。

• $x'=\frac{1+y}{1-y}$
• $y'=\frac{2}{\sqrt{a-d}}\cdot\frac{1+y}{x(1-y)}$
• $y'^2=x'^3+\frac{2(a+d)}{a-d}x'^2+x'$

※$x',y'$というのは導関数 ( 微分したもの ) ではなくて、変換後のパラメータを表します。
※$\sqrt{a-d}$をつけない形式の方が、実数の範囲で考えた場合、$a-d$が負でも虚数が発生せず対応し易いのですが、ここではこの変換で説明します。

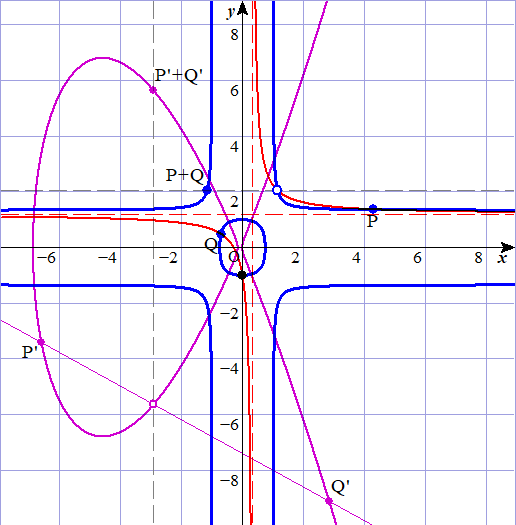
そうした場合、群としての演算はP,Qおよび点(0,-1)の3点を通る双曲線と曲線のもう1つの交点のx座標を反転した点をP+Qとするに変わります ( ただし、その2本の軸がそれぞれx軸,y軸に平行となるよう双曲線を選びます )。
次の図は、先ほどのモンゴメリ型$y^2=x^3+7x^2+x$に対応する、ツイスト化されたエドワーズ曲線の1つ$1.8x^2+y^2=1+x^2 y^2$ での群の演算 + の関係を可視化したものです。
※青がツイスト化されたエドワーズ曲線、紫がモンゴメリ型に対応しています

P,Qの座標をそれぞれ$(x_1,y_1),(x_2,y_2)$とした場合、P+Qの座標は$(\frac{x_1y_2+x_2y_1}{1+dx_1x_2y_1y_2},\frac{y_1y_2-ax_1x_2}{1-dx_1x_2y_1y_2})$と計算することができます。また、モンゴメリ型で単位元である無限遠点は(0,1)に移って来ています。

EdDSA/ed25519では、$GF(2^{255}-19)$におけるモンゴメリ型$y^2=x^3+486662x^2+x$のCurve25519を変換した、ツイスト化されたエドワーズ曲線$-x^2+y^2=1-\frac{121665}{121666}x^2y^2$ が利用されています。

単純な例

さて先ほどの話のように、ツイスト化されたエドワーズ曲線として楕円曲線を表現することで、群としての演算が$(\frac{x_1y_2+x_2y_1}{1+dx_1x_2y_1y_2},\frac{y_1y_2-ax_1x_2}{1-dx_1x_2y_1y_2})$として綺麗な形になるわけですが、これだけ見ても「どこが綺麗やねん?!」と思うかもしれません。

しかし、もっと単純な例を見てみると、実はとても意外なところにもこの曲線が関わっていることが分かります。

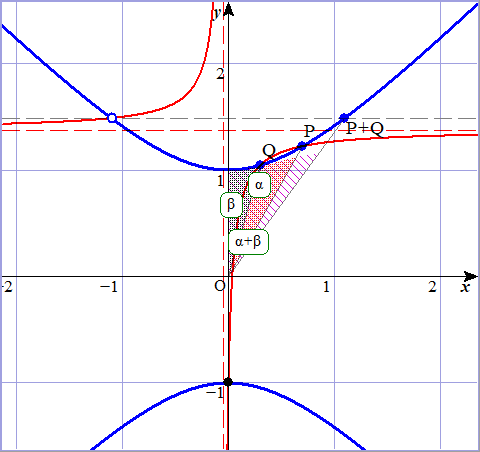
• 例1: 円と三角関数

次の図をご覧ください。「え? これただの円じゃん?」と思われた方、正解です。実は単位円 ( 原点中心、半径1の円 ) というのは、ツイスト化されたエドワーズ曲線の$a=1,d=0$にあたる例になっています。

この時の群としての演算は$(x_1y_2+x_2y_1, y_1y_2-x_1x_2)$、これって実は三角関数の加法定理$sin(\alpha+\beta)=sin\alpha cos\beta+sin\beta cos\alpha,~cos(\alpha+\beta)=cos\alpha cos\beta-sin\alpha sin\beta$ そのものだったりするのです。
ということで、角度の取り方がy軸から時計回りと、やや普通と異なりますが、$(sin\alpha,cos\alpha)+(sin\beta,cos\beta)=(sin(\alpha+\beta),cos(\alpha+\beta))$ が成立しています。三角関数の性質が、実は楕円曲線の作る群の性質として説明できるのです。

• 例2: 双曲線と双曲線関数

次は双曲線です。これは、$a=-1,d=0$にあたる例になっています。

この時の群としての演算は$(x_1y_2+x_2y_1, y_1y_2+x_1x_2)$、先ほどに良く似ていますが、こちらは双曲線関数の加法定理$sinh(\alpha+\beta)=sinh\alpha cosh\beta+sinh\beta cosh\alpha,~cosh(\alpha+\beta)=cosh\alpha cosh\beta+sinh\alpha sinh\beta$ に相当します。
双曲線関数なので、角度ではなく図中の網掛け部分の面積がパラメータになりますが、$(sinh\alpha,cosh\alpha)+(sinh\beta,cosh\beta)=(sinh(\alpha+\beta),cosh(\alpha+\beta))$ が成立しています。三角関数の話と同様、双曲線関数の性質も、楕円曲線の作る群の性質として説明できるということです。

なお、これらの話は黒木玄氏の最近のtweet楕円曲線のEdwards formについてを見て初めて知りました ( この記事では座標系の取り方が逆になっているので、比較する際はご注意下さい )。こうしてみると、楕円曲線というのも実は身近な存在だと思えるのではないでしょうか。

終わりに

まとめ

ということで、DSA/ECDSAとの対比という観点で説明してきました。なお、サンプルコードについてはEdDSAのサイトにpythonでの実装が紹介されています。

補足

この記事では、オリジナルの論文と記号の使い方を敢えて替えています。そのことで混乱を招くかもしれませんので、対照表を載せます。

項目	この記事での表記	論文での表記
楕円曲線による群	$G$	$E$
楕円曲線上の演算	$\circ,\omega^z,\prod$ ( 単独の演算、べき乗、複数要素の演算 )	$+, zW, \sum$ ( 加算、スカラー倍算、総和 )
群の単位元	$\epsilon$	$0$
楕円曲線のベースになる有限体	(登場せず)	$F_q$
ベースとなる要素とその位数	$\gamma,q$	$B,l$
スカラーの式の表現	$GF(q)$の加減乗除・等式で表現	$mod~l$の合同式で表現
ハッシュ関数	(登場せず)	$H(v_1,\cdots)$
ビット幅	(登場せず)	$b$ ( ハッシュ$H$のサイズは$2b$ビット )
秘密情報	$c$	$k$
署名鍵・検証鍵	$x,\chi=\gamma^x$	$a,A=aB$
鍵に関わる処理	$x=f_x(c)$	$a=2^{b-2}+\sum_{3\le i\le b-3} 2^i h_i$ なお、$(h_0,h_1,\cdots,h_{2b-1})=H(k)$
メッセージ	$m$	$M$
一時的な秘密情報	$k$	$r$
一時的な秘密情報の生成	$k=f_k(c,m)$	$r=H(h_b,\cdots,h_{2b-1},M)$ なお、$(h_0,h_1,\cdots,h_{2b-1})=H(k)$
署名	$(\rho,s)$	$R,S$
署名に関わる処理	$f_z(\rho,\chi,m)$	$H(R,A,M)$