はじめに
(注)私は量子コンピュータや量子情報に関する専門家ではありません.
不適切な表現等ありましたらご指摘いただけると幸いです.
皆さん量子コンピュータについてどんなイメージを持っていますか?
なんか難しそう,ニュースで聞くけどまだまだ実用には程遠いんじゃないの?そんなイメージをお持ちではないでしょうか?
そこでこの記事では,量子コンピュータが無料で使える「IBM Q」というサービスを利用して,素因数分解を一緒に解きながら,量子コンピュータの有用性について検証していきます.
IBM Qとは
IBMクラウドサービスが2017年に提供した,世界で初めての量子計算プラットフォームが「IBM Q」と呼ばれるサービスです.
ニューヨーク州にある大規模な冷却施設で管理された量子コンピュータを無料で誰でも使うことができます.

量子コンピュータの利用には簡単なユーザ登録が必要で,以下のサイトでわかりやすくまとめられているので,参考にしながら登録してみましょう.
以降,説明が長々続くので,もう待てない!早く素因数分解させて!という方は
「IBM Qによる実装」から進んでください.
素因数分解について
私たちが使っているようなコンピュータ(古典コンピュータ)では,大きい数字になればなるほど素因数分解を解くことが困難になります.(150~300桁の素数を用いた場合は,現時点で世界最速のコンピューターを使ったとしても,何十億年とかかるそうです.)
そこで,量子コンピュータの登場です.
量子コンピュータを使った「ショーアのアルゴリズム」を用いることで
素因数分解を多項式時間内で解くことができるようになります.
余談
余談ですが,現在世界で広く使われているRSA暗号(ログインとかsshのキーでよく使われている)は,素因数分解が難しいということを安全性の根拠としています.
例えば,P×Q = 6887となるような素数PとQを皆さんは思いつきますでしょうか?
きっと頭のいいTreasure生なら一瞬で導くことができると思いますが,
通常であれば,3,5,7,・・・で割り切れないか試していくと思います.(答えは71×97)
これが1~5桁ならまだしも,100桁~300桁になったらどうでしょうか?
1つ1つ素数で割っていっては,人生が何回あってもたりません.
ショーアのアルゴリズムを用いることで,多項式時間で解くことができる.
つまり,現在広く使われているRSA暗号の安全性の根拠が崩れてしまうということを意味しています.
しかし,後述する制限によって,現状そこまで脅威になっていないので、安心してください(笑)
ショーアのアルゴリズム
量子コンピュータを用いて素因数分解を多項式時間内で解くことができるのが
「ショーアのアルゴリズム」でした.
では早速,アルゴリズムの流れを以下の簡単な図でみてみましょう.
(わかりやすくしたかったので細かい部分ははぶきました.)

(1),(2),(4),(5)は皆さんのコンピュータ(古典コンピュータ)で簡単(多項式時間内)に解くことができますが,(3)で周期Tを求めることは容易ではありません.
古典コンピュータで周期を求めようとすると,便利なアルゴリズムが(いまのところ)存在しないため,総当たりで見つけることになります.
つまり,Nが大きくなればなるほど,周期を見つけるまでの時間が指数関数的に増大し多項式時間内に解くことが困難です.
そこで(3)では量子コンピュータを用いて周期Tを求めます.
IBM Qによる実装
IBM Qを早速使ってみましょう!
下準備
まずはじめに,以下のリンクにアクセスしてください.
https://quantumexperience.ng.bluemix.net/qx/editor
ユーザ登録orログインすると以下の画面になると思います.
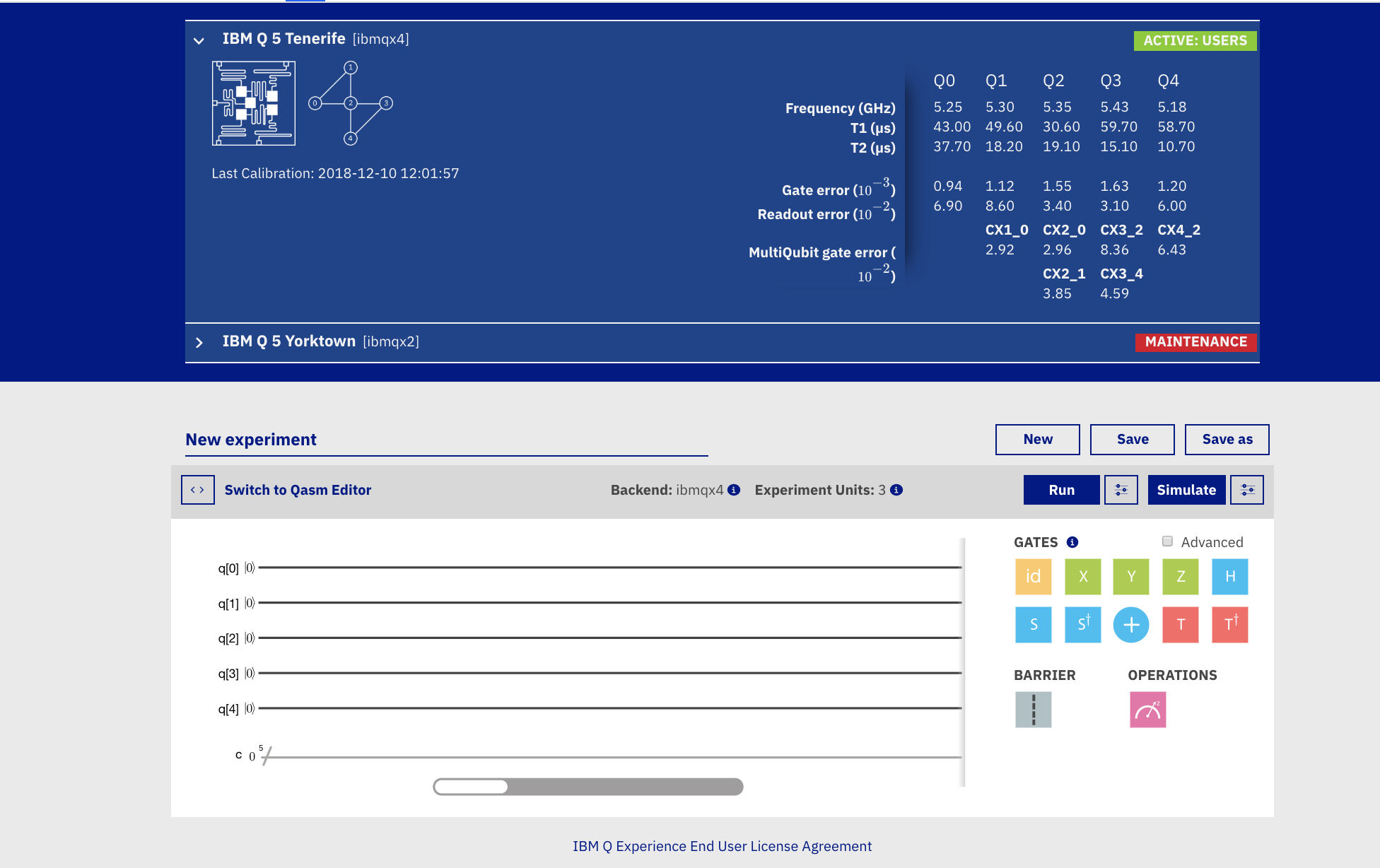
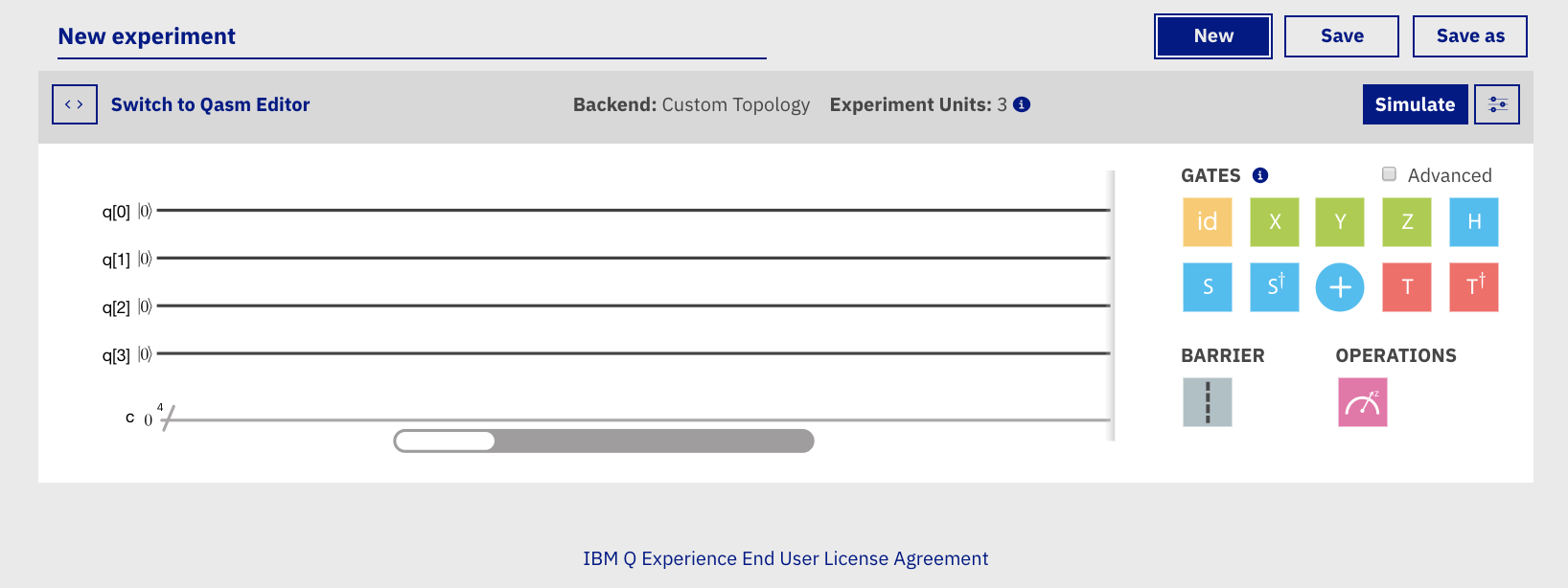
楽譜のように横に線が5本伸びていると思います.
この線1本が1つの量子ビットに対応し,この上に右のアイコン(演算子)を置くことで量子計算ができるようになります.

今回は,4量子ビットしか使わないので,エディターを以下のように編集してください.
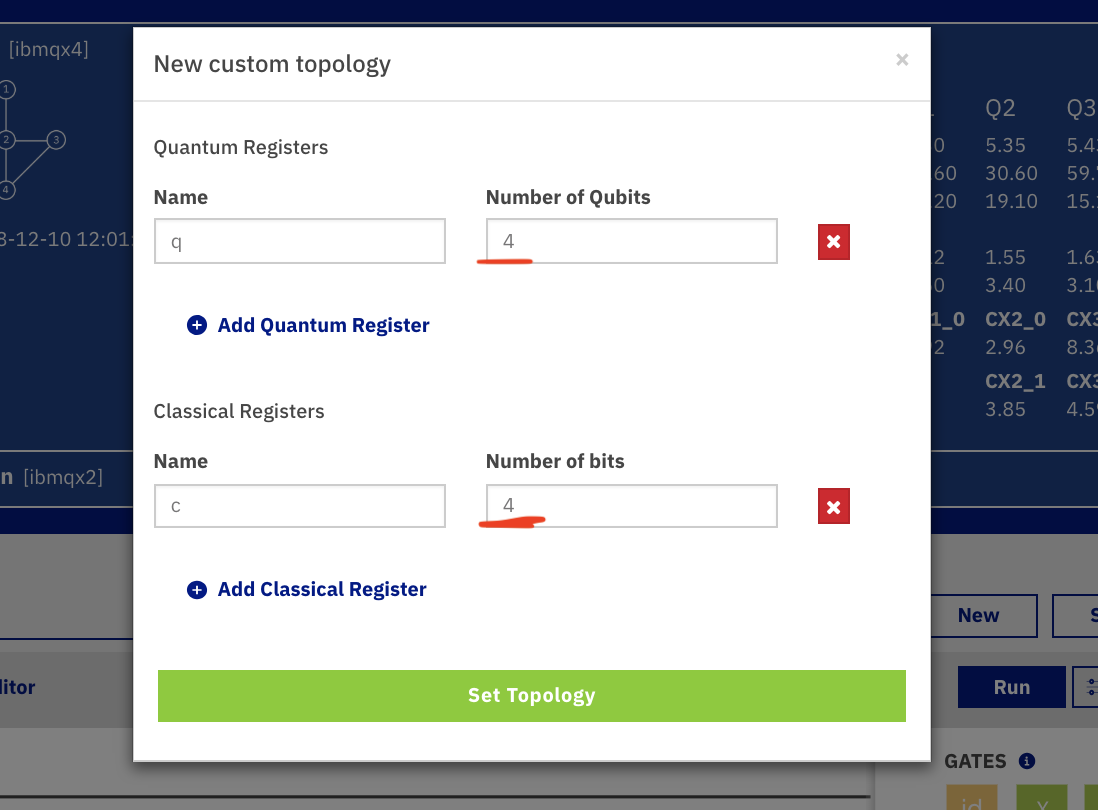
まず右上のNewを押して,「Custom Topology」を押してください.

次に,赤で強調されている部分の値を4に変え「Set Topology」を押します.
周期Tを発見する量子回路の実装
では,早速周期Tを求めるための量子回路を実装していきましょう.
まず,$f(x)=4^x(mod 15)$を表す量子回路を作成します.
(素因数分解したい自然数N=15,適当に選んだNより小さい数a=4とします.)
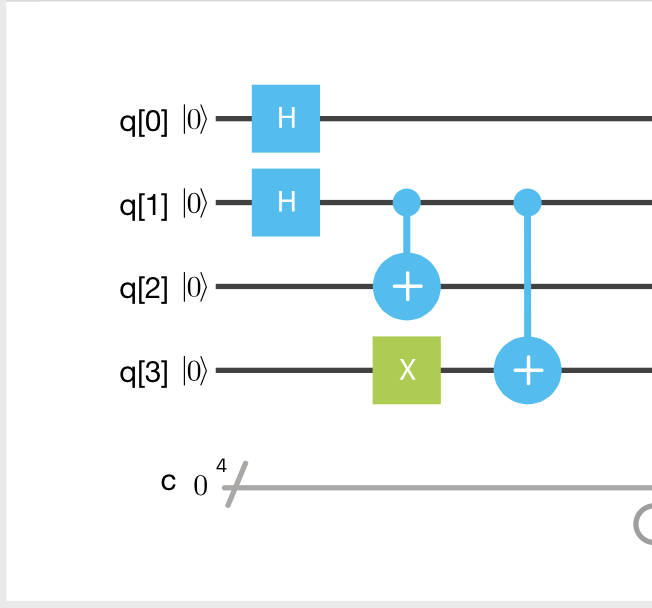
次に,先程作った回路を入力として,
今回のコアになる周期Tを求める量子回路をそのうしろに作成します.
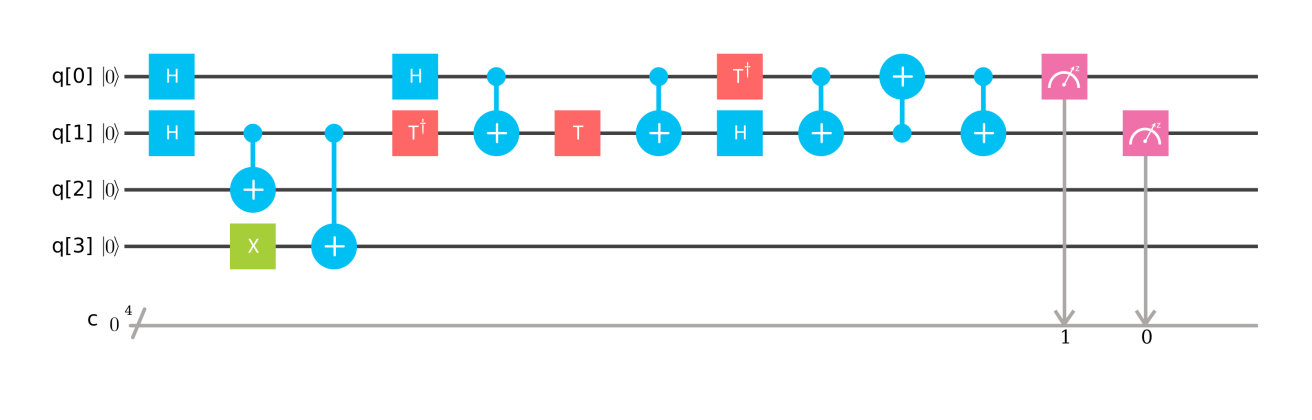
この量子回路では,入力に対して,量子フーリエ変換や逆量子フーリエ変換などなどを行っています.
細かい話は省略しますが,気になる方は以下の書籍に詳しく書かれているのでみてみてください!
作成した量子回路をシミュレーションで動かしてみましょう.
アイコンの上にある「Simulate」ボタンを押します.

縦軸が確率で,横軸が導出結果を表しています.
グラフからは,周期0が45%,周期2が55%の確率で導出されたことがわかると思います.
ここで,周期T=0はありえないので,答えは周期T=2となります.
これで,量子コンピュータをつかって周期T=2を求めることがました.
よって,$N=15,a=4$を求めた周期2を使って$a^{\frac{T}{2}}±1$に入れて因数を求めると,
$4^{\frac{2}{2}}+1=5,$ $4^{\frac{2}{2}}-1=3$
となり,$N=3\times5=15$で素因数分解できていることがわかります.
現実問題
簡単に素因数分解することができましたが,問題が一つあります.
それは,Nの数に応じて,量子ビットが必要ということです.
素因数分解したい数Nが2進数で$2^x$ビットとすると,周期を求めるために必要な量子ビットは$2x$です.
現在,amazonやgoogleなどのサービスで使われている暗号のビット数は$2^{10}$bit=1024bit以上で,
これを破るためには$2\times10=20$bit以上の量子ビットが必要です.
しかし,量子コンピュータはまだまだ未熟で,現段階ではそれほど多くの量子ビットを扱えるようなものを作れません.なので,量子コンピュータが実現したからといって今すぐ脅威になるということはありません.
おわりに
IBM Qを使って素因数分解を求めるために必要な周期を求めてみました.
現状,大きな数字の素因数分解をすることはできませんが,
ちょっとしたことならすぐ試すことができるので,皆さんもぜひこの機会に
量子コンピュータ完全に理解してみてはいかがでしょうか!