stan アドカレ 2019 24日目の記事
この記事は、Stan Advent Calendar 2019 24日目の記事です。
昨日は、 eiv11044_kwanseiさんの記事でした。
今回、使用したデータとコードは以下に置きました!!
https://osf.io/mn2sp/wiki/home/
始めに
---アニメ視聴中---
「(この声、能登さんか...)」
---ED中---
「早見さんやんけ!!」
ということありますよね(ないか)
今回は、実際に女性声優マップを作成した時に能登麻美子さんと早見沙織さんは似ている(近い)のかを検証しつつ、という記事です1
RQ
- 声優で地図をつくったときにどんな軸が出来るのか?
- 能登さんと早見さんは似てるのか?
手続き
- 女性声優24人のピックアップ
- 実験課題の作成とデータの収集
- ベイズ版INDSCALで女性声優のマップを作成
環境
R version 3.6.1 (2019-07-05)
Platform: x86_64-w64-mingw32/x64 (64-bit)
Running under: Windows 10 x64 (build 18362)
rstan_2.19.2
1. 女性声優24人のピックアップ
出来たら、たくさんの声優さんを使ってマッピングをしたいのですが、
今回は課題の程度を見て24人に絞らせていただきました。
ピックアップの方法
- 「2019 女性声優ランキング」でぐぐって、めぼしい4つのサイトからランキングを取得(スクレイピング)
- 各声優のランキングの平均値を算出
- 納得いかなかったので、自分の好みで選択2
今回用いた女性声優と代表作品3
| 声優 | 作品1 | 作品2 |
|---|---|---|
| 花澤香菜 | 青の祓魔師(杜山しえみ) | PSYCHO-PASS(常守朱) |
| 水瀬いのり | Re:ゼロから始める異世界生活(レム 役) | ダンまち(ヘスティア) |
| 佐倉綾音 | Charlotte(友利奈緒) | BanG Dream!(美竹蘭) |
| 悠木碧 | 魔法少女まどか☆マギカ(鹿目まどか) | 幼女戦記(ターニャ・デグレチェフ) |
| 内田真礼 | 中二病でも恋がしたい(小鳥遊六花) | ご注文はうさぎですか(シャロ) |
| 上坂すみれ | パパのいうことを聞きなさい!(小鳥遊空) | 無彩限のファントム・ワールド(川神舞) |
| 竹達彩奈 | ポプテピピック(ピピ美(2話Aパート)) | けいおん!(中野梓) |
| 雨宮天 | この素晴らしい世界に祝福を!(アクア) | 東京喰種(霧嶋董香) |
| 茅野愛衣 | あのはな(めんま) | ギルティクラウン(楪いのり) |
| 早見沙織 | 魔法科高校の劣等生(司波深雪) | 俺ガイル(雪ノ下雪乃) |
| 種田梨沙 | 四月は君の嘘(宮園かおり) | ゆゆ式(日向縁) |
| 東山奈央 | ゆるキャン△(志摩リン) | ニセコイ(桐崎千棘) |
| 水樹奈々 | NARUTO (日向ヒナタ) | 魔法少女リリカルなのは(フェイト) |
| 沢城みゆき | ローゼンメイデン(深紅) | ルパン三世(峰不二子) |
| 戸松遥 | ソードアート・オンライン(アスナ) | To LOVEる(ララ) |
| 日笠陽子 | ハイスクールD×D(リアス) | はたらく魔王さま!(エミリア) |
| 井口裕香 | とある魔術の禁書目録(インデックス) | ヤマノススメ(雪村あおい) |
| 堀江由衣 | Kanon(雪宮あゆ) | ひぐらしのなく頃に(羽入) |
| 小倉唯 | ゴブリンスレイヤー(女神官) | ロウきゅーぶ!(袴田ひなた) |
| 高橋李依 | FGO(マシュ) | からかい上手の高木さん(高木さん) |
| 釘宮理恵 | 銀魂(神楽) | 鋼の錬金術師(アルフォンス・エルリック) |
| 坂本真綾 | 空の境界(両儀式) | <物語>シリーズ(忍野忍) |
| 高垣彩陽 | D.C.Ⅱ(朝倉音姫) | 戦記絶唱シンフォギア(雪音クリス) |
| 能登麻美子 | 地獄少女(閻魔あい) | ケロロ軍曹(アンゴル=モア) |
※敬称略
「なんでスフィアの戸松と高垣は入ってるのに豊崎と寿はいないんだ」という声が聞こえる...
2. 実験課題の作成
jsPsychで作成した実験課題をfirebaseに設置し、オンラインで実験を実施。
ちなみに、Rmd×jsPsych×firebaseでのオンライン調査の方法のやり方をR Advent Calendar 2019 - Qiitaに投稿してあるので、そちらも合わせてご覧ください(ダイマ)↓↓↓
最初に、各声優の名前と代表作品を呈示して、知ってるかどうかの認知調査を行った後に、声優の並び替え課題を行ってもらいました。
こんな感じで、画面上に四角い枠とその中に24人の声優の名前が呈示されます。声優の声質が似ていると思ったら近くに配置、似ていないと思ったら遠くに配置する課題を参加者41人に行ってもらいました。
3. ベイズ版INDSCALで女性声優のマップを作成
INDSCALとは
INdividual Differences multidimensinal SCALing(INDSCAL)は、個人差多次元尺度構成法とも言い、文字通り個人差を考慮したMDSです。(INDSCALの読み方は、インスカルらしい)
MDSは、一対の対象距離データ(距離行列)を分析の対象とし、似た対象同士を近くに、似ていない対象同士を遠くにあるように配置することでアウトプットとして対象の座標情報、すなわち地図(マップ)を得ることが出来ます。今回の場合は、似ている声優同士は近くに、そうでない声優同士は遠くに配置される地図が得られると考えてください。
その際に、声優の声に対する感性は個人によって異なるため、個人差を考慮した地図を作ろうというのが個人差多次元尺度構成法(INDSCAL)です。INDSCALでは、地図上の次元は共通であると仮定し、個人ごとに次元の重み(重要度)を表現することが可能です。この次元軸の伸縮をもって個人差を考慮するのがINDSCALの利点であると思います。
今回は、声優の並び替え課題で、個人ごとに各声優の座標データを取得しています。個人が並び替えた時点でマップは出来ているのですが、声質の軸は与えていないため、並び替えた個人ごとに声優の位置はバラバラです。なので、声優の座標データから声優間の距離を算出し、距離行列から地図を作ろうというのが今回の目的です。
座標→距離→座標というステップを踏んでいることになります。
この記事の最後に参考文献も載せておきます。
モデル
今回使用したモデルは、北大路書房さんの『たのしいベイズモデリング』第7章「心の旅が始まる」を参考にしています。
対象(声優)$x$と$y$には本当の距離$\delta_{xy}$があり、観測時には誤差が伴うため、
$$
d_{xy} \sim Normal(\delta_{xy},\sigma^2)
$$
と考えられます。各声優は座標を持っており、声優$x$は$\lambda_{x1}$,$\lambda_{x2}$、声優$y$は$\lambda_{y1}$,$\lambda_{y2}$で表現
するとしたとき、(ユークリッド)距離$\delta_{xy}$は
$$
\delta_{xy}=\sqrt{(\lambda_{x1}-\lambda_{y1})^2+(\lambda_{x2}-\lambda_{y2})^2} \ =\sqrt{\sum_{p=1}^2(\lambda_{xp}-\lambda_{yp})^2}
$$
という式で計算可能です。INDSCALではこの距離の座標に、個人ごとの重みがついており、個人$i$の次元$p$に対する重みを$w_{ip}$で表現すると仮定した時、対象間の距離$\delta{xyi}$は
$$
\delta_{xyi}=\sqrt{\sum_{p=1}^2W_{ip}(\lambda_{xp}-\lambda_{yp})^2}
$$
で表現されます。
stanコード
推定に用いたstanコードはこちら
data{
int<lower=1> N; //被験者数
int<lower=1> I; //刺激の数(観光地、声優の数)
int<lower=1> P; //刺激のペア数(24C2)
int<lower=1> G; //世代の総数(重みづけするグループ)
int<lower=1> Gid[N]; //世代のデータセット
row_vector<lower=0>[P] Y[N]; //
}
parameters{ //制約のない座標パラメータ
real fix_x1;
real fix_y1;
real<lower= -10,upper= 0> fix_x2;
real fix_y2;
real<lower= -10,upper= 0> fix_x3;
real<lower= -10,upper= 0> fix_y3;
real<lower= -10,upper= 0> fix_x4;
real<lower= -10,upper= 0> fix_y4;
real<lower= -10,upper= 0> fix_x5;
real<lower= 0,upper= 10> fix_y5;
real<lower= -10,upper= 0> fix_x6;
real<lower= 0,upper= 10> fix_y6;
real<lower= -10,upper= 0> fix_x7;
real<lower= -10,upper= 0> fix_y7;
real fix_x8;
real<lower= -10,upper= 0> fix_y8;
real<lower=0,upper= 10> fix_x9;
real<lower=-10,upper= 0> fix_y9;
real<lower=0,upper= 10> fix_x10;
real<lower=0,upper= 10> fix_y10;
real<lower=-10,upper= 0> fix_x11;
real<lower=0,upper= 10> fix_y11;
real<lower= -10,upper= 0> fix_x12;
real fix_y12;
real<lower=0,upper= 10> fix_x13;
real<lower=-10,upper= 0> fix_y13;
real<lower=0,upper= 10> fix_x14;
real<lower=0,upper= 10> fix_y14;
real<lower=0,upper= 10> fix_x15;
real<lower=-10,upper= 0> fix_y15;
real<lower=0,upper= 10> fix_x16;
real fix_y16;
real fix_x17;
real<lower=0,upper= 10> fix_y17;
real<lower=0,upper= 10> fix_x18;
real<lower=0,upper= 10> fix_y18;
real<lower=-10,upper= 0> fix_x19;
real<lower=-10,upper= 0> fix_y19;
real<lower=-10,upper= 0> fix_x20;
real<lower=0,upper= 10> fix_y20;
real<lower= -10,upper= 0> fix_x21;
real<lower= -10,upper= 0> fix_y21;
real<lower=0,upper= 10> fix_x22;
real<lower=0,upper= 10> fix_y22;
real<lower=0,upper= 10> fix_x23;
real<lower=0,upper= 10> fix_y23;
real<lower=0,upper= 10> fix_x24;
real<lower=-10,upper= 0> fix_y24;
simplex[G] w0[2];
real<lower=0> sig;
}
transformed parameters{
vector[G] w[2];
vector[I] const_lambda[2]; //制約を入れたパラメータセット
vector[I] lambda[2]; //最終的に推定する座標セット
const_lambda[1,1] = fix_x1;
const_lambda[2,1] = fix_y1;
const_lambda[1,2] = fix_x2;
const_lambda[2,2] = fix_y2;
const_lambda[1,3] = fix_x3;
const_lambda[2,3] = fix_y3;
const_lambda[1,4] = fix_x4;
const_lambda[2,4] = fix_y4;
const_lambda[1,5] = fix_x5;
const_lambda[2,5] = fix_y5;
const_lambda[1,6] = fix_x6;
const_lambda[2,6] = fix_y6;
const_lambda[1,7] = fix_x7;
const_lambda[2,7] = fix_y7;
const_lambda[1,8] = fix_x8;
const_lambda[2,8] = fix_y8;
const_lambda[1,9] = fix_x9;
const_lambda[2,9] = fix_y9;
const_lambda[1,10] = fix_x10;
const_lambda[2,10] = fix_y10;
const_lambda[1,11] = fix_x11;
const_lambda[2,11] = fix_y11;
const_lambda[1,12] = fix_x12;
const_lambda[2,12] = fix_y12;
const_lambda[1,13] = fix_x13;
const_lambda[2,13] = fix_y13;
const_lambda[1,14] = fix_x14;
const_lambda[2,14] = fix_y14;
const_lambda[1,15] = fix_x15;
const_lambda[2,15] = fix_y15;
const_lambda[1,16] = fix_x16;
const_lambda[2,16] = fix_y16;
const_lambda[1,17] = fix_x17;
const_lambda[2,17] = fix_y17;
const_lambda[1,18] = fix_x18;
const_lambda[2,18] = fix_y18;
const_lambda[1,19] = fix_x19;
const_lambda[2,19] = fix_y19;
const_lambda[1,20] = fix_x20;
const_lambda[2,20] = fix_y20;
const_lambda[1,21] = fix_x21;
const_lambda[2,21] = fix_y21;
const_lambda[1,22] = fix_x22;
const_lambda[2,22] = fix_y22;
const_lambda[1,23] = fix_x23;
const_lambda[2,23] = fix_y23;
const_lambda[1,24] = fix_x24;
const_lambda[2,24] = fix_y24;
lambda[1,] = const_lambda[1,]/(sqrt(dot_self(const_lambda[1,]))); //ノルムを整える
lambda[2,] = const_lambda[2,]/(sqrt(dot_self(const_lambda[2,])));
for(g in 1:G){
for(j in 1:2){
w[j,g] = w0[j,g]*G;
}
}
}
model{
row_vector[P] d[N];
for(n in 1:N){
int pos=0;
for(p in 1:(I-1)){
for(q in (p+1):I){
pos = pos +1;
d[n,pos] = 0;
for(j in 1:2){
d[n,pos] = d[n,pos] + w[j,Gid[n]]*(lambda[j,p]-lambda[j,q])^2;
}
d[n,pos] = sqrt(d[n,pos]);
}
}
Y[n] ~ normal(d[n],sig);
}
//prior
fix_x1 ~ normal(0,1);
fix_y1 ~ normal(0,1);
fix_x2 ~ normal(0,1);
fix_y2 ~ normal(0,1);
fix_x3 ~ normal(0,1);
fix_y3 ~ normal(0,1);
fix_x4 ~ normal(0,1);
fix_y4 ~ normal(0,1);
fix_x5 ~ normal(0,1);
fix_y5 ~ normal(0,1);
fix_x6 ~ normal(0,1);
fix_y6 ~ normal(0,1);
fix_x7 ~ normal(0,1);
fix_y7 ~ normal(0,1);
fix_x8 ~ normal(0,1);
fix_y8 ~ normal(0,1);
fix_x9 ~ normal(0,1);
fix_y9 ~ normal(0,1);
fix_x10 ~ normal(0,1);
fix_y10 ~ normal(0,1);
fix_x11 ~ normal(0,1);
fix_y11 ~ normal(0,1);
fix_x12 ~ normal(0,1);
fix_y12 ~ normal(0,1);
fix_x13 ~ normal(0,1);
fix_y13 ~ normal(0,1);
fix_x14 ~ normal(0,1);
fix_y14 ~ normal(0,1);
fix_x15 ~ normal(0,1);
fix_y15 ~ normal(0,1);
fix_x16 ~ normal(0,1);
fix_y16 ~ normal(0,1);
fix_x17 ~ normal(0,1);
fix_y17 ~ normal(0,1);
fix_x18 ~ normal(0,1);
fix_y18 ~ normal(0,1);
fix_x19 ~ normal(0,1);
fix_y19 ~ normal(0,1);
fix_x20 ~ normal(0,1);
fix_y20 ~ normal(0,1);
fix_x21 ~ normal(0,1);
fix_y21 ~ normal(0,1);
fix_x22 ~ normal(0,1);
fix_y22 ~ normal(0,1);
fix_x23 ~ normal(0,1);
fix_y23 ~ normal(0,1);
fix_x24 ~ normal(0,1);
fix_y24 ~ normal(0,1);
sig ~ student_t(4,0,5);
}
(なげー)
MDSは、距離しか情報がないため制約を与えないと座標軸が定まらなくなるという性質があります。制約がないと、マップは自由に動くし回転するので、対象のいずれかに画びょうを刺すことで、その動きを止めるイメージです(え?)。
参考にしたコードでは、対象のうち4点を第一象限、第二象限、第三象限、原点に固定することで、その性質を克服しています。しかし、私のデータではうまくいかず、声優たちが原点に集まってしまうので、一度{smacof}パッケージでINDSCALを行い、その座標から各対象の象限情報を取得し、制約として与えています(長くてスミマセン)。
この辺をいい感じにする方法知ってる方がいたら教えてほしいですm(_ _"m)
データ
jsPsychから取得したデータを整形し、各声優間の距離を算出。
推定に用いたデータは以下の形式です。今回は、24人の声優を全員知っている参加者14名を対象に推定を行いました。(スパースデータへのINDSCALは勉強中です...。参加してくださった皆様すみません!!)
データの形式は以下の通りです。
| ID | 花澤香菜_水瀬いのり | 花澤香菜_佐倉綾音 | 花澤香菜_悠木碧 | 花澤香菜_内田真礼 |
|---|---|---|---|---|
| 6 | 0.4234724 | 0.3749724 | 0.4643496 | 0.2439673 |
| 4 | 0.2060646 | 0.1713398 | 0.8797659 | 0.4298948 |
| 5 | 0.5896066 | 0.2362668 | 0.5406340 | 0.2666604 |
| 13 | 0.2516097 | 0.2476994 | 0.3016558 | 0.6164902 |
| 14 | 0.4431288 | 0.7861026 | 0.5168333 | 0.3031742 |
声優は24人いるため、組み合わせが276通りあるので276(通り)×14(人)のデータとなります。
推定
# 必要なパッケージの読み込み
library(tidyverse)
library(ggrepel)
library(rstan)
options(mc.cores = parallel::detectCores())
rstan_options(auto_write = TRUE)
# Bayesian INDSCAL --------------------------------------------------------
# ファイルからデータを読み込む
dis_umr <- read.csv("data/distance.csv")
# Bayesian INDSCAL
# Stanに渡すデータセットに組み上げる
dataset <- list(N=nrow(dis_umr), ## 被験者の数
I=24, ## 刺激の数
P=choose(24,2), ## 刺激のペアの数
Y=as.matrix(dis_umr[2:ncol(dis_umr)]), ## データセット
Gid=dis_umr$ID, ## 世代のID
G=max(Gid)) ## 世代の総数
# モデルのコンパイル
model <- stan_model("stan/INDSCAL.stan")
# サンプリング
fit <- sampling(model,dataset,iter=10000,warmup=5000)
iter=10000,warmup=5000でMCMCを行い、トレースプロットと$\hat{R}<1.1$となっていたことから、収束したと判断しました。
推定された2019年女性声優マップと解釈
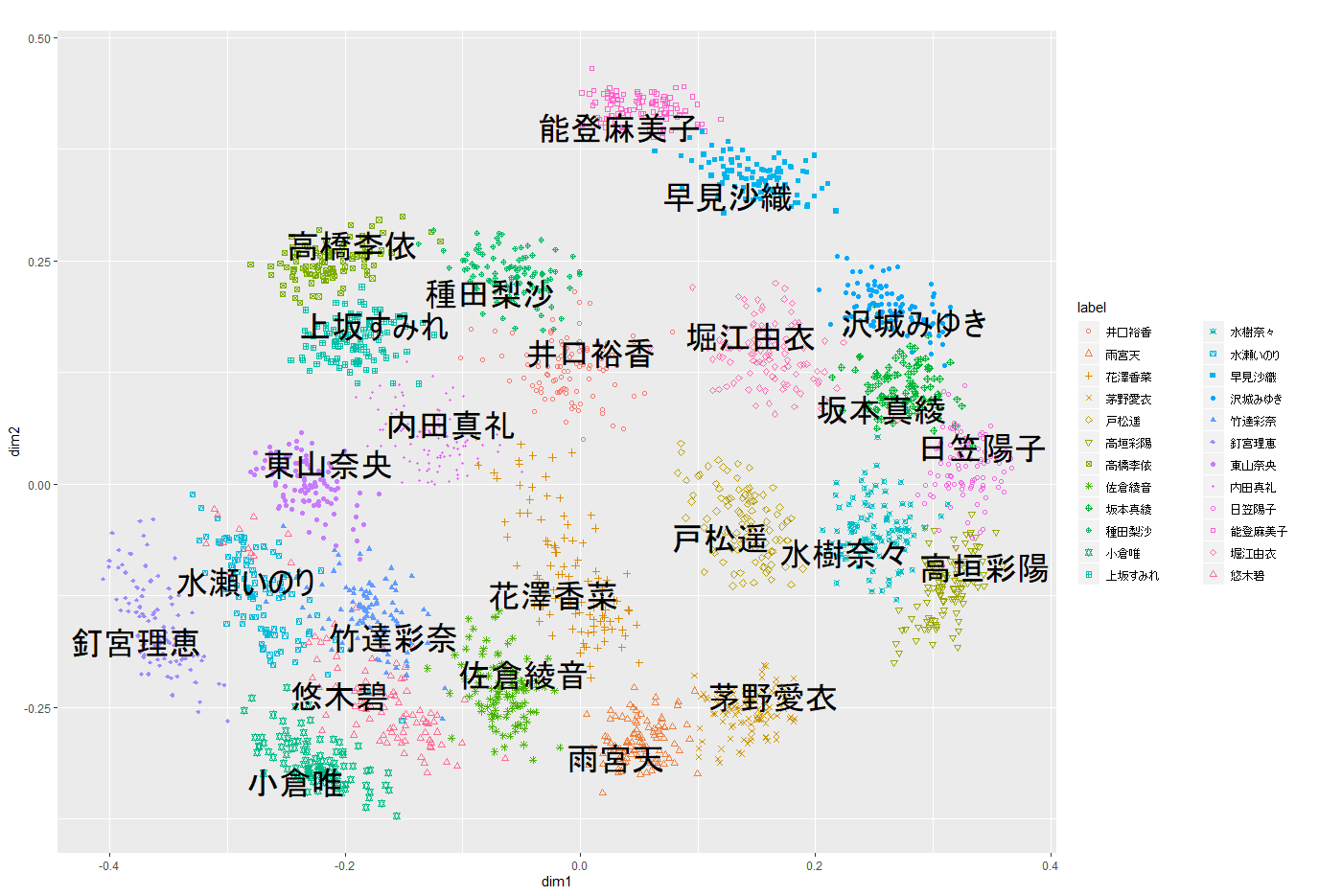
推定され各声優の座標パラメータ事後予測平均からマップを作成。同時にMCMCサンプルからランダムに100点ずつ抜き出し同時にプロット。
# 作業1:布置図の描画準備 --------------------------------------------------------
## Stanfit objectからMCMCサンプルを取り出してデータフレームに
fit %>% rstan::extract() %>% data.frame() %>%
## 座標パラメータだけ取り出す
dplyr::select(starts_with("lambda")) %>%
## ロング型データに
tidyr::gather(key,val) %>%
## 次元,対象変数を変数名から作成,不要な列の削除
mutate(dim=str_sub(key,start=8,end=8),
target=str_sub(key,start=10),
key=NULL) %>%
## 対象,次元でグループ化,ネスト
dplyr::group_by(target,dim) %>%
nest() %>%
## 次元を横に広げ,ネスト解除
tidyr::pivot_wider(names_from = dim,values_from = data,) %>%
unnest() %>%
## 改めて対象でグループ化
group_by(target) %>%
## 変数名をわかりやすく
rename(X=val,Y=val1) %>%
# 要約統計量の算出
dplyr::summarise_all(funs(EAP=mean,
lower=quantile(.,0.25),
upper=quantile(.,0.75))) %>%
mutate(target = as.numeric(target)) %>%
arrange(target) %>%
## 対象名を因子型にしラベルをつける
mutate(target=factor(1:24,
labels=c("花澤香菜","水瀬いのり","佐倉綾音","悠木碧",
"内田真礼","上坂すみれ","竹達彩奈",
"雨宮天","茅野愛衣","早見沙織","種田梨沙",
"東山奈央","水樹奈々","沢城みゆき","戸松遥",
"日笠陽子","井口裕香","堀江由衣","小倉唯",
"高橋李依","釘宮理恵","坂本真綾","能登麻美子",
"高垣彩陽"))) -> plot.df
# 作業2:雲を纏わせるプロットの準備 --------------------------------------------------------------
## MCMCサンプルの中から一部を抽出
## 抽出するサンプル数
nsamp <- 100
## Stanfit objectからMCMCサンプルを取り出してデータフレームに
fit %>% rstan::extract() %>% data.frame %>%
## 座標パラメータだけ取り出す
dplyr::select(starts_with("lambda")) %>%
## MCMCサンプルからサンプリング
sample_n(.,size=nsamp) %>%
## 変数名を列名から取り込む
tibble::rownames_to_column() %>%
## ロング型データに
tidyr::gather(key,val,-rowname) %>%
## 対象名を変数につける
mutate(label=rep(rep(c("花澤香菜","水瀬いのり","佐倉綾音","悠木碧",
"内田真礼","上坂すみれ","竹達彩奈","雨宮天",
"茅野愛衣","早見沙織","種田梨沙","東山奈央",
"水樹奈々","沢城みゆき","戸松遥","日笠陽子",
"井口裕香","堀江由衣","小倉唯","高橋李依",
"釘宮理恵","坂本真綾","能登麻美子","高垣彩陽"),
each=nsamp*2))) %>%
## 次元変数を作成
mutate(dim=paste0("dim",str_sub(key,start=8,end=8))) %>%
## 不要な変数を削除
mutate(key=NULL) %>%
## 次元を横に並べる
tidyr::spread(dim,value=val) -> cloud.df
# 描画 ----------------------------------------------------------------------
# 雲に色をつける
## 元になる座標は作業1の座標
ggplot(data=plot.df,aes(x=X_EAP,y=Y_EAP)) +
## 色付きの雲を纏わせる
geom_point(data=cloud.df,aes(x=dim1,y=dim2,shape=label,color=label),alpha=1) +
## シェイプの種類がデフォルトを超えるのでマニュアルで指定
scale_shape_manual(values=1:24) +
## 対象名をプロット
geom_text_repel(data=plot.df,aes(x=X_EAP,y=Y_EAP,label=target),size=7) +
## X,Y軸に名前をつける
labs(x="dim1",y="dim2")
マップ上の声優名は事後予測平均の座標を示し、雲は散らばり具合を示します。
能登さんと早見さん近い!!
MCMCのサンプル点(色のついた雲)は、座標ばらつきを示しており、ここでは参加者が声優に対して持っているイメージと考えることもできます。つまり、能登さんや早見さんはばらつきが小さいのでイメージを確立しており、花澤さんや東山さんはばらつきが大きいので演じる幅が広いという解釈もできるのではないでしょうか。
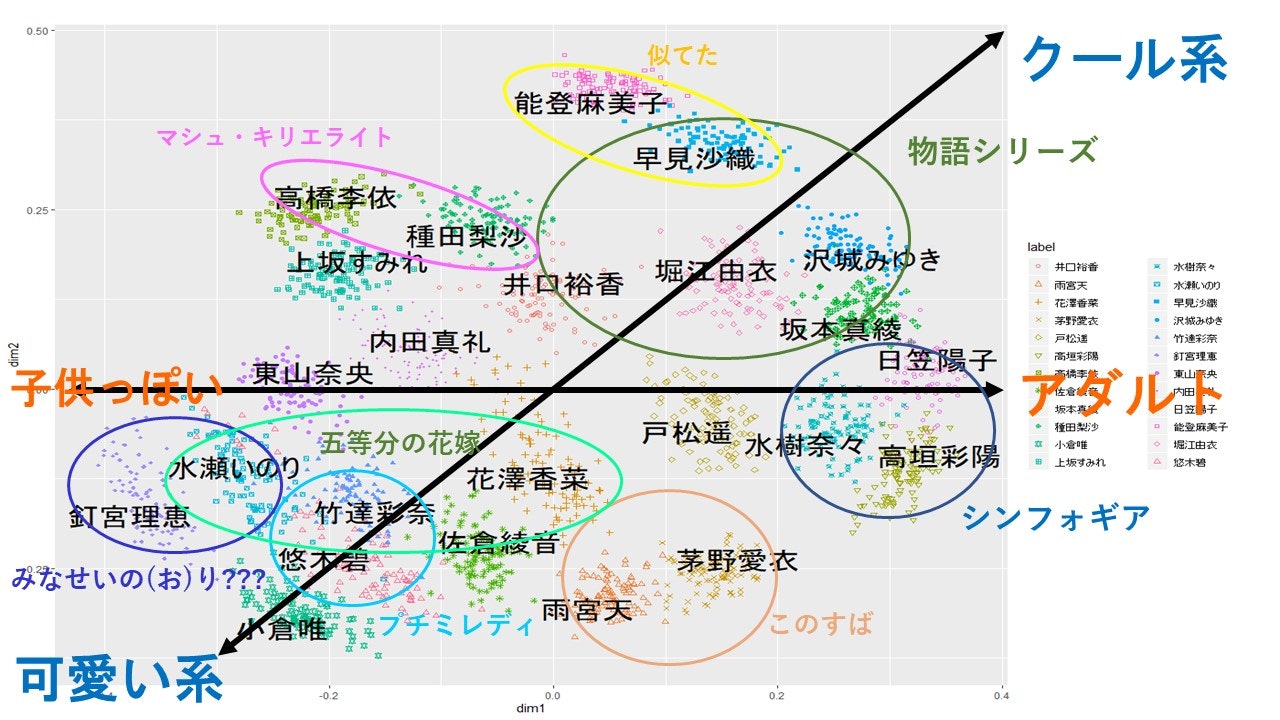
軸の解釈
次元軸の解釈ですが、横軸は年齢?と思いましたが釘宮さんが、めっさ左にいるので違いそう(え?釘宮さんは永遠の16歳?)。となると、演じる役のタイプ?
マップの左側ほど、子供だったり若い役を演じることが多く、右側はアダルトな役を演じていそうな傾向があります。
縦軸は、なんでしょう。天さんと能登さんが対極...
識者がいたら教えてください。
縦軸は難しいですが、第一象限はクール系(ほっちゃん?)、第三象限は可愛い系の声質イメージがある気がします。
五等分の花嫁のヒロイン4人(水瀬いのり・佐倉綾音・花澤香菜・竹達彩奈)はみんな第三象限にいますね。
第一・第三象限を通るy=xを見たら、クール系と可愛い系に分けられそう。第二・第四象限の声優はどっちもやってるイメージ(偏見)
※INDSCAL(MDS)は軸の解釈は見る人に依存するので、絶対的な正解は有りません
声優同士の塊
象限の制約を与えてますが、なんかうまい感じに分かれていますね。
個人的な解釈をすると...
-
上坂すみれと井口裕香・内田真礼共演本数が多い
-
井口裕香と内田真礼はサンカレアラジオの共演してる
-
高橋李依と種田梨沙は性質が近いから同じキャラ(FGOのマシュ)を演じているのか、それとも逆の因果?
-
釘宮理恵と水瀬いのりは、釘宮理恵がアイマスで「水瀬伊織」というキャラを演じていて、名前が似てるから説
-
堀江由衣、坂本真綾、早見沙織は物語シリーズのヒロインたち(花澤さんも)
-
日笠陽子、水樹奈々、高垣彩陽はシンフォギア繋がり
-
悠木碧と竹達彩奈はユニット(プチミレディ)を組んでる
-
茅野愛衣と雨宮天はこのすば?(高橋李依は?)
このように性質というより、声優間の距離は共演作品やユニットに引っ張られている可能性が高い。
ここまでをまとめると
このような情報が得られるのかなと思います。これが絶対的な正解というわけではありません。アニメや声優に詳しい人ならもっと有益な情報を得ることが出来ると思います。
個人ごとの軸の重み
個人ごとの評価軸の重みの事後予測平均は以下の通り
| id | w.1 | w.2 |
|---|---|---|
| 1 | 0.7111316 | 1.2284293 |
| 2 | 1.2349330 | 0.7952984 |
| 3 | 1.1470615 | 0.9112868 |
| 4 | 0.6559200 | 1.1947805 |
| 5 | 1.5812522 | 0.4937991 |
| 6 | 1.2413844 | 0.7949524 |
| 7 | 1.5806774 | 0.5125111 |
| 8 | 1.0528295 | 0.8011546 |
| 9 | 0.5667555 | 1.3860546 |
| 10 | 1.0450253 | 0.8195517 |
| 11 | 1.3410758 | 0.6177751 |
| 12 | 0.8770712 | 1.0996945 |
| 13 | 0.5012203 | 1.7451259 |
| 14 | 0.4636623 | 1.5995861 |
今回は、解釈が難しいので端折りますが、こういったように個人ごとに対象への評価に対する重みは違うことが分かります。また、今回は個人差で行いましたが年代や性別などのグループを割り振ることで群間の特徴も把握することが可能です。
終わりに
能登さんと早見さんは似てました!!
女性声優マップを作成した時、声優同士の距離はユニットや共演作品に引っ張られる可能性があり、声質で分けるのは難しい(プロなのでいろんな役を演じ分けてますしね)。ただ、個人的な解釈をするとしたら、声が可愛い系かクール系かと演じるキャラの年齢傾向でマップが構成されてる気もします。
この記事を見てる皆さんも、このマップを見ながら解釈をするクリスマスイブを送れば、盛り上がるのではないでしょうか。
INDSCAL(MDS)は探索的であり、答えや意味を自分で見出さなければいけないのは非常に面白いです。得られた地図を見る人によって異なるインプリケーションが得られるのも魅力的です。
スパースなMDSのやり方とstanコードなどアドバイスいただけると助かります。
明日はkosugittiさんの記事です。
参考文献
第7章「こころの旅が始まる」 stanコードやINDSCALの説明が載っていてわかりやすい。データ構造をモデルに適用できる形に整形すればmcmcすぐできるので楽。本では、10の観光地のINDSCALを行っている。
第5章「多次元尺度構成法」 MDSについて基本的な情報が載っている。たのしいベイズモデリングは説明が簡易的部分があるので、この本でMDSの理論を学んで後にたのしいベイズモデリングに移行すると、たのしいベイズモデリングが出来る
-
ちなみに筆者は、「四月は君の嘘」の能登麻美子さんと「FGO 牛若丸」の早見沙織さんが好きである(こういう縦に長い記事で注釈あるのうざいよね、すみません)。 ↩
-
ちなみに筆者は、雨宮天・夏川椎菜・麻倉ももからなる声優ユニット「try sail」が好きであるが、認知度の点から今回は天さん以外ピックアップから外した。2019年の夏に幕張で行われたtry sailのライブに行こうとしたところ、法事と被り、複雑な気分過ぎて膝から崩れ落ちたのは記憶に新しい。 ↩
-
女性声優と代表作品の選出に際して、協力頂いた大学の某先輩には感謝申し上げたい。5時間にもわたる議論が行われ、白熱しすぎて少しケンカになりそうだった... ↩