この記事は、Stan Advent Calender 2019の23日目の記事です。
はじめまして。Stan初心者です。
大学院で社会心理学を専攻しており、ただいま絶賛修論執筆中です。
修論で使ったモデルを今回記事にしてみました。
はじめに
みなさんは、学生時代「夏休みの宿題めんどくさいな~。明日からがんばろ」なんて後回しにした経験はありませんか?某国民的アニメの主人公の弟のカツオだって夏休みの宿題を後回しにした挙句、8月31日に波平やマスオに手伝ってもらって慌てて終わらせるのは毎年の恒例行事になっていますよね。このように、「今宿題をするめんどくさ」よりも「あとで宿題をするめんどくささ」の方が小さく感じることを遅延価値割引と言います。
遅延価値割引ってつまりどういうこと?
遅延価値割引は、よく経済学や心理学の分野で取り上げられ研究されています。一番有名なのは、なんといってもマシュマロ実験でしょう 。
マシュマロ実験とは、子供の前にマシュマロを一つ置いて一人にした時、その子供は食べることを我慢できるかどうかをテストした実験です。子供たちは、ある一定時間を我慢したらマシュマロを2個もらえるよ、と言われていますが、一人残された子供の中には我慢することができず食べちゃう子もいます。これは、あとでもらえる2個のマシュマロよりも今食べる1個のマシュマロの方が、価値があると考えた結果だと考察されています。つまり、あとでもらえる2個のマシュマロの価値が時間の経過によって下がったということです。
本題:双子で遅延価値割引って違うの?
このマシュマロ実験は、子供の家庭の社会階層が大きく結果に作用することが知られています 。家庭の環境が子供の遅延価値割引に影響する。なんともおもしろい結果ですよね。このように、遅延価値割引の程度は人によって個人差があります。
だとすると、同じ家庭環境で育ち、かつ年齢も同じ双子の価値割引はどうなるのでしょうか。もちろん同じ親に育ててもらい、同じものを食べ、一緒に成長しているのですから同じように遅延価値割引をしていてもおかしくないですよね?そこで、実際に双子の遅延価値割引について測定し、その程度が違うのかどうか調べてみました。
測定方法
回答者:筆者と双子の姉
私たちは以下の質問について答えました。
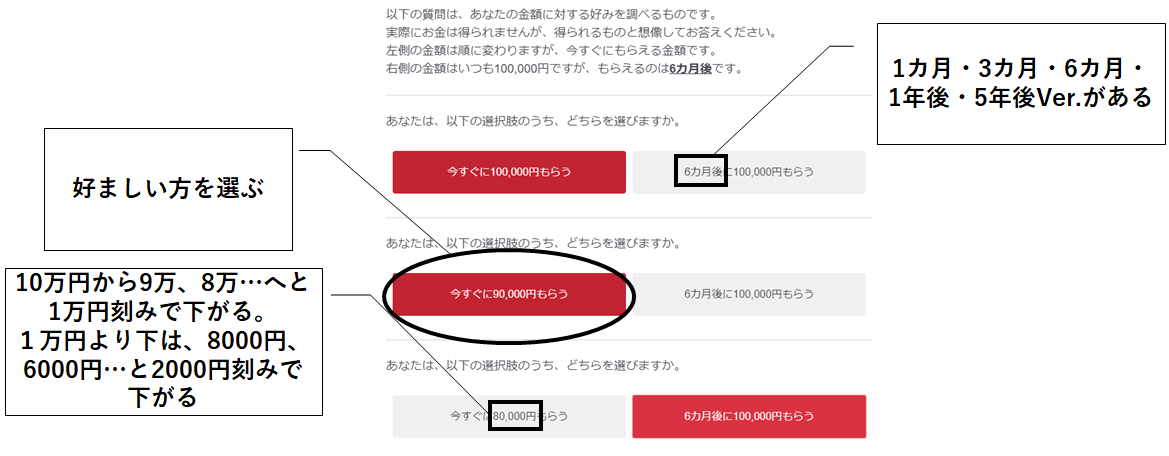
図のように金額に関する二つの選択肢を提示し、好ましいと思う方を選択してもらいました。
このとき、左側の選択肢は**常に今すぐもらえますが、金額が変わります。100,000円からスタートして次に90,000円、80,000円と1万円ずつ下がっていきます。そして1万円まで下がった時、次は8,000円、6,000円の…のように2,000円ずつ下がり、最終的に「今すぐ0円もらえる」という選択肢になります。
一方、右側の選択肢はもらえる時期が遅れますが、常に100,000円もらえます。**もらえる時期は1か月後、3か月後、6か月後、1年後、5年後の5種類あります。
※ちなみになんで10万円スタートにしたかというと、姉が「5万円やったら迷わへんけど、10万・9万あたりやったら迷うわ」って言ったからです。私はたとえ2万円でも今すぐほしいのに、そんな余裕な心を持っていて羨ましいですね。
よって、回答者は15(金額の種類)×5(もらえる時期) = 225通りの質問を答えることになります。
選択肢が2つなので、答えるのは意外と楽です。
さて、二人の回答が終われば準備は完了です。
このデータをもとに遅延価値割引を推定しました。
モデル
遅延価値割引の推定にあたって、「双曲割引」や「指数割引」などいくつかのモデルが提唱されています。その中でも今回は社会科学のためのベイズ統計モデリング の9章で紹介されていた主観時間・指数割引モデルを採用しました。モデルの詳しい説明は本書に分かりやすく書かれていますので、ここでは割愛させていただきます。簡単に説明すると、報酬がもらえるまでの将来の時間を、客観的な時間よりも近く見積もる程度を考慮したモデルです。
モデルの式は以下の通り。
P_{j(i)} =Bernoulli(θ_{j(i)}^d)
θ_{j(i)}^d=logistic (β\{U_j (A^d )-U(A_i^s )\})
U(A_i^s )=A_i
U_j (A^d )=5000*exp\{-k_j d^{s_j}\}
$i$は項目、$j$は個人の添え字を表しています。
- 1番目の式
遅延報酬を選択する確率を表しています。選択する確率はパラメータ$θ_{j(i)}^d$のベルヌーイ分布に従います。 - 2番目の式
パラメータ$θ_{j(i)}^d$を規定するモデルです。βは逆温度パラメータです。 - 3・4番目の式
即時報酬$U(A_j^s )$と遅延報酬$U_j (A^d )$の価値を表します。即時報酬は提示された金額の大きさがそのまま反映されますが、遅延報酬は主観的時間にそって、指数的に価値が割り引かれていきます。ちなみに$k$が割引率です。大きいほど将来の価値を小さく見積もっているということです。
モデルの推定
それでは、さっそく推定をしていきましょう
まずは非階層モデルから推定していきます。
- 非階層モデル
非階層モデルのスタンコードはこちらから(▶をクリック)
data{
int N;
int Trial;
real D[Trial];
real amount_soon[Trial];
int amount_delay;
int<lower=0,upper=1> Y[N,Trial];
}
parameters{
real k_raw[N];
real beta_raw[N];
real s_raw[N];
}
transformed parameters{
real k[N] = exp(k_raw);
real beta[N] = exp(beta_raw);
real s[N] = exp(s_raw);
}
model{
for(n in 1:N){
for(t in 1:Trial){
real v_delay = amount_delay*exp(-k[n]*D[t]^s[n]);
real v_soon = amount_soon[t];
target += bernoulli_logit_lpmf(Y[n,t] | beta[n]*(v_delay - v_soon));
}
}
target += normal_lpdf(k_raw | 0, 5);
target += normal_lpdf(beta_raw | 0, 5);
target += normal_lpdf(s_raw | 0, 5);
}
generated quantities{
vector[N] log_lik = rep_vector(0, N);
for(n in 1:N){
for(t in 1:Trial){
real v_delay = amount_delay*exp(-k[N]*D[t]^s[N]);
real v_soon = amount_soon[t];
log_lik[n] += bernoulli_logit_lpmf(Y[n,t] | beta[N]*(v_delay - v_soon));
}
}
}
遅延価値割引の推定結果(非階層モデル)
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
k[1] 0.01 0.00 0.02 0.00 0.00 0.00 0.01 0.06 19066 1
k[2] 0.24 0.00 0.06 0.13 0.20 0.24 0.28 0.38 6779 1
非階層モデルの結果の詳細はこちらから(▶をクリック)
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
k_raw[1] -6.18 0.03 2.51 -12.25 -7.54 -5.65 -4.31 -2.84 6098 1
k_raw[2] -1.46 0.00 0.30 -2.05 -1.63 -1.44 -1.28 -0.96 4266 1
beta_raw[1] 0.20 0.00 0.37 -0.51 -0.05 0.20 0.45 0.92 7287 1
beta_raw[2] 0.35 0.00 0.30 -0.24 0.15 0.35 0.56 0.94 9145 1
s_raw[1] -3.51 0.04 3.09 -10.97 -5.33 -2.83 -1.03 0.36 4949 1
s_raw[2] -0.74 0.00 0.23 -1.24 -0.87 -0.73 -0.60 -0.35 5766 1
k[1] 0.01 0.00 0.02 0.00 0.00 0.00 0.01 0.06 19066 1
k[2] 0.24 0.00 0.06 0.13 0.20 0.24 0.28 0.38 6779 1
beta[1] 1.31 0.01 0.50 0.60 0.95 1.22 1.57 2.52 5466 1
beta[2] 1.49 0.00 0.46 0.78 1.16 1.42 1.75 2.56 9503 1
s[1] 0.26 0.01 0.41 0.00 0.00 0.06 0.36 1.44 3488 1
s[2] 0.49 0.00 0.11 0.29 0.42 0.48 0.55 0.70 4073 1
log_lik[1] -87.60 0.26 27.17 -151.23 -102.91 -83.55 -68.10 -46.21 11100 1
log_lik[2] -13.41 0.02 1.40 -16.97 -14.02 -13.05 -12.42 -11.88 5657 1
lp__ -39.40 0.03 1.93 -43.98 -40.42 -39.07 -38.02 -36.55 5845 1
ちゃんと収束しました。ただ、k[1]とk[2]の推定値を見てみると、二人でまったく異なっています。これは、もしや階層モデルの方がうまくフィットするかもしれません。ということで、階層モデルで推定してみました。
- 階層モデル
階層モデルのスタンコードはこちらから(▶をクリック)
data{
int N;
int Trial;
real D[Trial];
real amount_delay;
real amount_soon[Trial];
int<lower = 0, upper = 1> Y[N, Trial];
}
parameters{
real k_raw[N];
real k_mu;
real<lower = 0> k_sigma;
real s_raw[N];
real s_mu;
real<lower = 0> s_sigma;
real beta_raw[N];
real<lower = 0> beta_sigma;
real beta_mu;
}
transformed parameters{
real k[N] = exp(k_raw);
real s[N] = exp(s_raw);
real beta[N] = exp(beta_raw);
}
model{
for(n in 1:N){
for(t in 1:Trial){
real v_delay = amount_delay*exp(-k[n]*D[t]^s[n]);
real v_soon = amount_soon[t];
target += bernoulli_logit_lpmf(Y[n,t] | beta[n]*(v_delay - v_soon));
}
}
target += normal_lpdf(k_raw | k_mu, k_sigma);
target += normal_lpdf(k_mu | 0, 5);
target += cauchy_lpdf(k_sigma | 0, 5) - cauchy_lccdf(0 | 0, 5);
target += normal_lpdf(s_raw | s_mu, s_sigma);
target += normal_lpdf(s_mu | 0, 5);
target += cauchy_lpdf(s_sigma | 0, 5) - cauchy_lccdf(0 | 0, 5);
target += normal_lpdf(beta_raw | beta_mu, beta_sigma);
target += normal_lpdf(beta_mu | 0, 5);
target += cauchy_lpdf(beta_sigma | 0, 5) - cauchy_lccdf(0 | 0, 5);
}
generated quantities{
vector[N]log_lik = rep_vector(0, N);
for(n in 1:N){
for(t in 1: Trial){
real v_delay = amount_delay*exp(-k[n]*D[t]^s[n]);
real v_soon = amount_soon[t];
log_lik[n] = bernoulli_logit_lpmf(Y[n, t] | beta[n]*(v_delay - v_soon));
}
}
}
遅延価値割引の推定結果(階層モデル)
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
k[1] 0.01 0.00 0.02 0.00 0.00 0.00 0.01 0.06 8939 1.00
k[2] 0.24 0.00 0.06 0.13 0.19 0.23 0.27 0.37 4487 1.00
階層モデルの結果の詳細はこちらから(▶をクリック)
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
k_raw[1] -8.86 0.28 9.43 -30.36 -9.93 -6.10 -4.33 -2.82 1106 1.00
k_raw[2] -1.48 0.00 0.28 -2.07 -1.64 -1.46 -1.30 -0.98 4227 1.00
k_mu -2.64 0.05 3.18 -8.89 -4.40 -2.74 -1.03 4.51 4297 1.00
k_sigma 7.24 0.23 10.03 0.97 2.61 4.54 8.18 30.17 1897 1.00
s_raw[1] -3.41 0.11 6.06 -17.41 -4.09 -1.52 -0.60 0.77 2854 1.00
s_raw[2] -0.73 0.00 0.22 -1.20 -0.86 -0.72 -0.59 -0.35 4235 1.00
s_mu -1.22 0.04 2.47 -6.91 -2.22 -0.93 -0.22 4.00 4288 1.00
s_sigma 3.87 0.11 6.45 0.08 0.87 2.20 4.69 17.33 3735 1.00
beta_raw[1] 0.24 0.00 0.34 -0.44 0.01 0.24 0.46 0.93 5127 1.00
beta_raw[2] 0.33 0.00 0.28 -0.22 0.15 0.32 0.52 0.88 5478 1.00
beta_sigma 1.69 0.04 2.59 0.03 0.32 0.87 2.13 8.01 3565 1.00
beta_mu 0.27 0.03 1.44 -3.02 -0.13 0.29 0.71 3.41 1974 1.00
k[1] 0.01 0.00 0.02 0.00 0.00 0.00 0.01 0.06 8939 1.00
k[2] 0.24 0.00 0.06 0.13 0.19 0.23 0.27 0.37 4487 1.00
s[1] 0.42 0.01 0.69 0.00 0.02 0.22 0.55 2.16 3408 1.00
s[2] 0.49 0.00 0.10 0.30 0.42 0.49 0.55 0.70 4208 1.00
beta[1] 1.34 0.01 0.48 0.64 1.01 1.27 1.58 2.52 4384 1.00
beta[2] 1.45 0.01 0.42 0.81 1.16 1.38 1.68 2.42 5462 1.00
log_lik[1] 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 16261 1.00
log_lik[2] -0.10 0.00 0.10 -0.37 -0.14 -0.07 -0.04 -0.01 5869 1.00
lp__ -48.35 0.12 3.85 -56.52 -50.79 -48.15 -45.68 -41.30 1027 1.01
遅延価値割引率自体は階層モデルも非階層モデルも変わりません。
ベイズファクターを計算すると、
(参考サイト)
library(bridgesampling)
bs_nonclass <- bridge_sampler(fit_delay_nonclass)#非階層モデルの自由エネルギー
bs_class <- bridge_sampler(fit_delay_class)#階層モデルの自由エネルギー
BF <- bf(bs_class, bs_nonclass)
print(BF)
Estimated Bayes factor in favor of bs_class over bs_nonclass: 0.68484
これは、非階層モデルに対して、階層モデルを0.68倍支持するということです。これの逆数をとると、1.46倍です。このことから、非階層モデルの方が若干支持されますが、ベイズファクターの基準(BF>3)から考えてもそれほど明確な違いがないといえます。つまり、非階層モデルの方がよいというわけではありません。
と、結論を下してしまうのは軽率です。そもそも階層モデルを使うには、もっとサンプルサイズが必要です。今回は二人でも収束しましたが、収束をしないことも多いそうです。全国の双子の遅延価値割引を測定して、ペアデータを分析するのもおもしろいかもしれませんね。
おわりに
今回協力してもらった姉に「謝辞を書け」と言われているので書きます。
ご協力ありがとうございました![]()
参考資料
Watts, T. W., Duncan, G. J., & Quan, H. (2018). Revisiting the Marshmallow Test: A Conceptual Replication Investigating Links Between Early Delay of Gratification and Later Outcomes. Psychological Science, 29(7), 1159–1177.
Mischel, W., & Ebbesen, E. B. Antonette, R. Z (1972). Cognitive ans Attentional Mechanisms in Delay Gratification. Journal of Personality and Social Psychology, 21(2), 204–218.
浜田宏・石田淳・清水裕士(2019) 『社会科学のためのベイズ統計モデリング』 朝倉書店