Abstract
昔話題になったAlphaGoではDQNという強化学習の一手法が用いられています。強化学習はゲームやロボット制御の分野でよく研究されていますが、医学研究でも活用されているのを知ったので紹介を兼ねて実装してみたいと思います。今回はTD法を用いて薬物依存の原因とされている報酬系(ドーパミン神経)をモデル化していきましょう。
Introduction
ここでは計算論的精神医学の簡単な紹介とモデル化の概要にとどめます。(強化学習についてはわかりやすい記事があるのでそちらを読んでください。Actor Critic法はこれか「Pythonで学ぶ強化学習」がわかりやすいと思います。)
計算論的精神医学
計算論的精神医学とは、精神障害患者の示す特徴的な行動や神経活動に関して、その背景にあるプロセスを理論的な制約と物理的な制約を反映させた数理モデルによって明らかにするという、計算論的アプローチを用いて精神障害の研究を行う学問領域である。
(「計算論的精神医学」第2章より)
現代精神医学の問題として、
- 疾病分類の問題
- バイオマーカーの問題
- 説明のギャップ
が挙げられます。
例えば、「幻覚や妄想は精神病で重複して観察されるので、幻覚や妄想が診断の指標にはならないのでは?」、「血中の白血球数を調べるといった客観的かつ定量的な診断ができないので、ほとんど患者自身の主観的体験の報告と行動観察に基づいて診断が行われるとその信頼性は怪しくない?」、「ドーパミン関連遺伝子とかドーパミンニューロンの精神回路についての研究成果はたくさんあるけど、ドーパミンが統合失調症にどう関与するかはまだわからないです...。」(ドーパミンD2受容体ブロッカーが統合失調症に効果があると判明したのは終戦直後なので、もう70年近く経っている。)といった問題があります。
それらの問題を解決するために、計算で人間の脳をモデル化しよう!というのが計算論的精神医学です。
薬物依存の数理モデル化
「計算論的精神医学」では、Redishによる研究が紹介されています。今回はそれを参考にしてモデル化と実装を行います。
薬物依存症とは、薬物の効果が切れてくると、薬物が欲しいという強い欲求(渇望)がわいてきて、その渇望をコントロールできずに薬物を使ってしまう状態をいいます。薬物依存ともいいます。
(厚生労働省HP)
薬物に依存してしまうのは単純に薬物を得た際の報酬が高いからだとすると、薬物の快楽が薄れてもやめられないという依存状態を説明できません。ここでRedishは強化学習のActor Critic法を用いてTD誤差の拡張をすることで依存をモデル化しました。(ここでは元論文のような連続的な時間ではなく書籍と同じく段階的に状態遷移するモデルを考えます。)
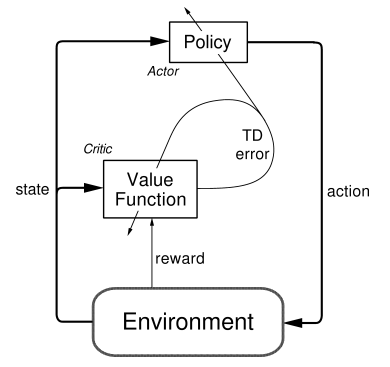
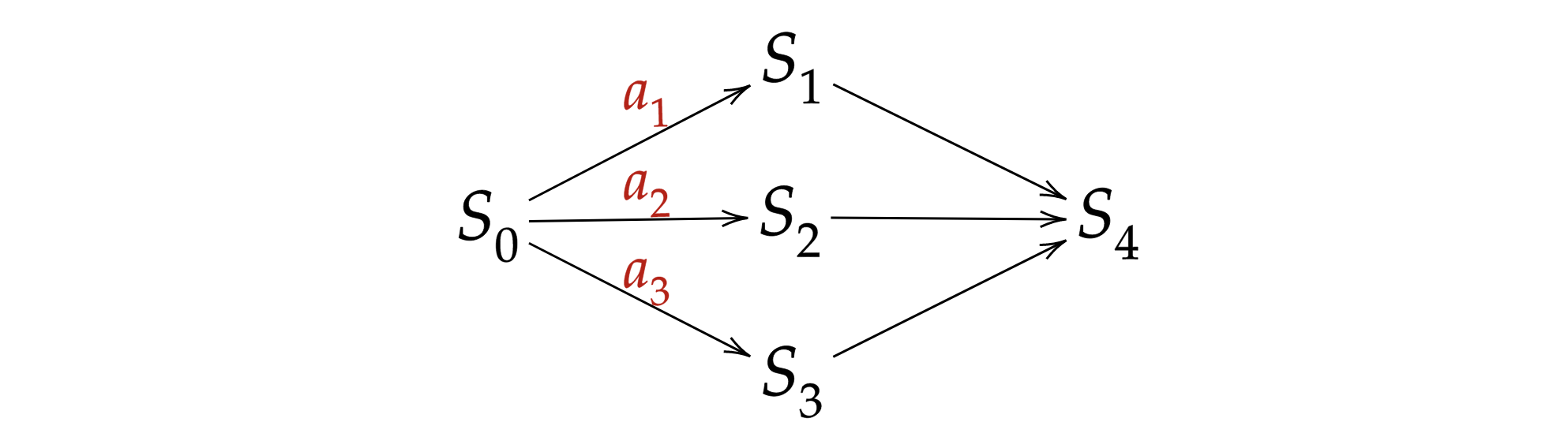
まず、環境を設定します。眼の前にピーマン、チョコケーキ、コカインがおいてある状態$S_0$を考えます。ここでエージェントは戦略$\pi_t(s_t)$に従って行動$a_1, a_2, a_3$から1つを選択します。行動$a_1, a_2, a_3$はそれぞれ「ピーマンを食べる」、「ケーキを食べる」、「コカインを摂取する」とし、行動後は状態$S_1, S_2, S_3$に遷移します。状態$S_1, S_2, S_3$ではそれぞれ食べたものに応じて報酬$R_1, R_2, R_3$が与えられます。そこでTD誤差を用いて状態価値$V_t(s_t)$と戦略$\pi_t(s_t)$を更新し、その後エージェントは状態$S_4$に遷移します。状態$S_4$は日常生活に相当し、食べたものに関係なく一定の報酬$R_4$が与えられます。もう一度同じく状態価値$V_t(s_t)$と戦略$\pi_t(s_t)$を更新します。以上が1エピソードで合計200エピソード繰り返します。
普通のActor Critic法では状態価値$V_t(s_t)$と戦略$\pi_t(s_t)$を以下のように更新します。
V_{t+1}(s_t) = V_t(s_t) + \alpha_C\delta_t
\\
\pi_{t+1}(s_t) = \pi_t(s_t) + \alpha_P\delta_t
\\
\delta_t = r_t + \gamma V_t(s_{t+1}) - V_t(s_t)
$\alphaは学習率、\gammaは割引率を表します。$
ここではTD誤差$\delta_t$を薬物による過渡的なドーパミンの増加$D(s_t)$を用いて
\delta_t = max\{r_t + \gamma V_t(s_{t+1}) - V_t(s_t) + D(s_t), D(s_t)\}
**とすることで、薬物を摂取したときに$\delta_t$は最低でも正の値を持ち、状態価値は増加し続けます。**薬物を選択した場合以外では$D(s_t)=0$とします。
「計算論的精神医学」では強化学習だけでなく、他にもノーベル賞を受賞したHodgkin-Huxleyモデルなどの生物物理学モデル、ニューラルネットワークモデル、ベイズ推論モデルによるうつ病、統合失調症、ASD、PTSDなどのモデル化事例も紹介されているので、気になった方は是非図書館で借りるか買ってみてください。
実装
- Ubuntu 18.04 LTS
- Python 3.6.7
「Pythonで学ぶ強化学習」を参考に実装。説明はコメントアウトします。
import numpy as np
import copy
import matplotlib.pyplot as plt
import seaborn as sns
plt.style.use('default')
sns.set()
sns.set_style('whitegrid')
np.random.seed(0)
環境(rewardsとdopamineを調整することで色々な結果が得られます。)
class DrugOrTreat:
def __init__(self, rewards=[0.0, 1.0, 1.5, 0.5, 0.2], dopamine=1.0):
self.rewards = rewards
self.dopamine = dopamine
def step(self, action): #行動に報酬を与える
done = False
if action == len(self) - 1:
done = True
reward = self.rewards[action]
return reward, done
def __len__(self):
return len(self.rewards)
Actorクラス
class AddictActor():
def __init__(self, env):
self.actions = list(range(1, len(env) - 1)) # 行動の種類
self.Q = np.zeros(len(env) - 2) # 行動の評価値
self.num_actions = [0] * len(self.actions) # それぞれの行動回数を記録
self.actor_log = []
def policy(self, state):
if state == 0: # softmax関数で選択
a = np.random.choice(self.actions, 1,
p=np.exp(self.Q) / np.sum(np.exp(self.Q), axis=0))
return a[0]
else:
return len(self.actions) + 1
def log(self, action):
if action <= len(self.actions): # 初期状態からの遷移のみ記録
self.num_actions[action - 1] += 1
self.actor_log.append(copy.copy(self.num_actions))
Criticクラス
class AddictCritic():
def __init__(self, env):
self.V = np.zeros(len(env)) # 5つの状態価値を記録
self.critic_log = []
def log(self, action):
if action <= len(self.V) - 2: # 初期状態からの遷移のみ記録
self.critic_log.append(copy.copy(self.V))
Actor Critic法クラス
class ActorCritic():
def __init__(self, actor_class, critic_class):
self.actor_class = actor_class
self.critic_class = critic_class
def train(self, env, max_episode=200, gamma=0.9, lr=0.1):
actor = self.actor_class(env)
critic = self.critic_class(env)
for e in range(max_episode):
state = 0
done = False
while not done:
action = actor.policy(state) # 戦略に基づいて行動選択
next_state = action
reward, done = env.step(action) # 報酬の受け取り
gain = reward + gamma * critic.V[next_state]
estimated = critic.V[state]
if state == len(env) - 2: # 薬物摂取時のTD誤差
td = max(gain - estimated + env.dopamine, env.dopamine)
else: #それ以外でのTD誤差
td = gain - estimated
if action <= len(actor.Q): # 初期状態からの遷移のみ更新
actor.Q[action - 1] += lr * td
critic.V[state] += lr * td
actor.log(action)
critic.log(action)
state = next_state
return actor.actor_log, critic.critic_log
訓練用のヘルパー関数と訓練
def train_ac(max_episode=200, rewards=[0.0, 1.0, 1.5, 0.5, 0.2], dopamine=1.0):
trainer = ActorCritic(AddictActor, AddictCritic)
env = DrugOrTreat(rewards=rewards, dopamine=dopamine)
return trainer.train(env, max_episode=max_episode)
actor_log, critic_log = train_ac()
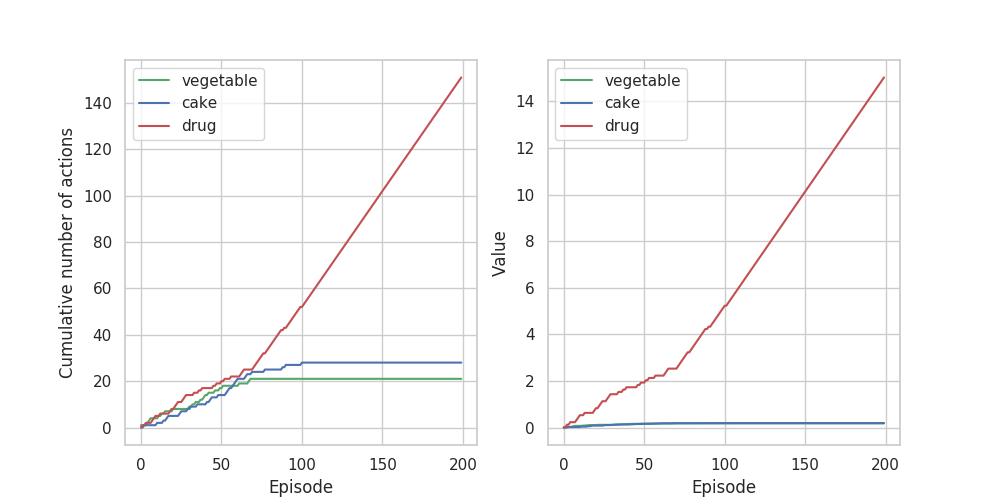
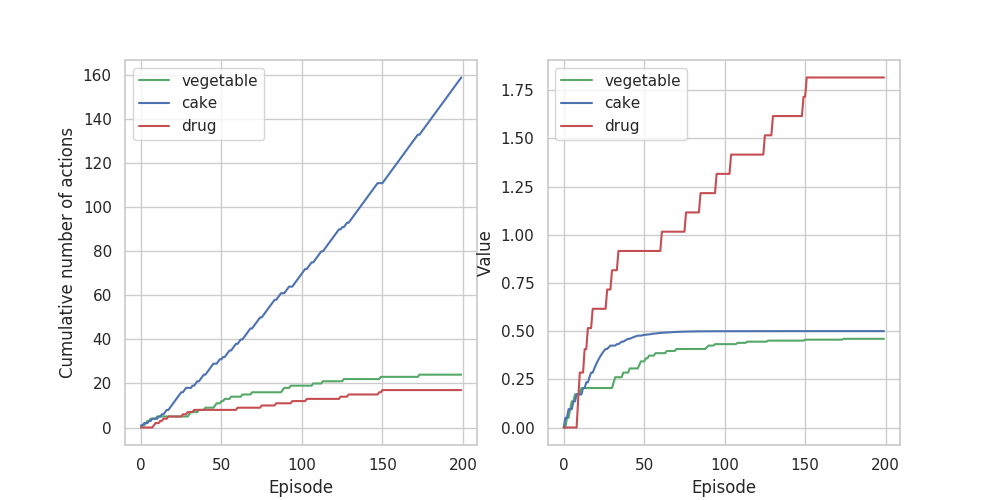
累積行動選択回数と状態価値のグラフを描きます。
x = np.arange(200)
fig = plt.figure(figsize=(10, 5))
ax1 = fig.add_subplot(1, 2, 1)
ax1.plot(x, [a[0] for a in actor_log], color='g', label='vegetable')
ax1.plot(x, [a[1] for a in actor_log], color='b', label='cake')
ax1.plot(x, [a[2] for a in actor_log], color='r', label='drug')
ax1.legend()
ax1.set_xlabel("Episode")
ax1.set_ylabel("Cumulative number of actions")
ax2 = fig.add_subplot(1, 2, 2)
ax2.plot(x, [c[1] for c in critic_log], color='g', label='vegetable')
ax2.plot(x, [c[2] for c in critic_log], color='b', label='cake')
ax2.plot(x, [c[3] for c in critic_log], color='r', label='drug')
ax2.legend()
ax2.set_xlabel("Episode")
ax2.set_ylabel("Value")
plt.show()
ちなみに、dopamine=0.0(ドーパミンの過渡的上昇無効)では、
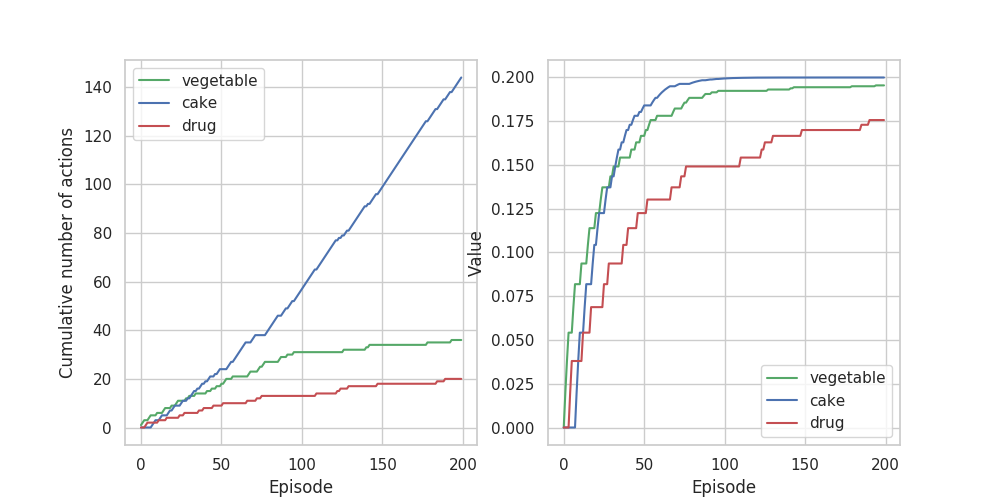
さらに、dopamine=1.0に戻してrewards[4]=0.5(日常の報酬を増加)とすると、
Discussion
薬物によるドーパミンの過渡的上昇を考慮した上段のグラフでは、70エピソードから薬物の選択回数が一気に増加しています。状態価値のグラフでは最初から薬物の価値がほか2つとは大きく離れているのにもかかわらず、70エピソードまでは行動選択回数に大きな違いは見られません。これはActor Critic法が戦略と状態評価を別個に考えているからだと考えられます。Q-learningなどのValueベースで実装すればもっと早い段階から薬物の行動回数が増えると思います。(Valueベースは定められた戦略ではなく価値が最大となる状態に遷移することを前提に行動するので他の報酬による抑止が働かず、最初から薬物を選び続ける。)
中段ではドーパミンの過渡的上昇効果をなくすと、薬物依存に陥らないことが確認できます(ケーキ依存になってるけど......。)。状態価値は終了後の報酬である0.2に収束しています。
下段では、終了後の報酬を大きくすることで、薬物の状態価値が大きくなっているのにもかかわらず行動回数は増加せずに依存を回避できていることがわかります。日常生活を充実させれば薬物を使っても依存しにくいということかな?
ドーパミンの作用を考慮したTD誤差の拡張によって薬物依存がモデル化できました。薬物依存症について知られている知見として、他の報酬による抑止効果は早い段階の方が効果が大きいこと、薬物以外の報酬の価値が大きいほど依存しにくくなることが挙げられます。グラフからこれらの特徴が再現できていることが分かります。
強化学習を用いて精神疾患をモデル化することの問題点として、「計算論的精神医学」第3章では
- 強化学習モデル自体は具体的な神経回路や生物学的な基盤をモデル化したものではなく、将来の報酬と罰の予測と将来の報酬を最大化する行動の選択の学習をモデル化しているため、抽象度が高い。
- 抽象度が高くパラメータの数が少ないのでモデルフィッティングはしやすいが、得られた知見を神経回路などの具体的な問題と結びつけるのは注意が必要である。また、従来の精神医学の問題である「説明のギャップ」を埋めるためには他のモデルとの併用が必要。
ということが述べられています。単純化しすぎも良くないってことですね。例えば、薬物依存には、精神依存、身体依存、耐性の3つがあります。耐性というのは身体が薬物に順応することで同じ快楽を得るために必要な用量が増えることで、活性量と致死量が近い薬剤の場合、耐性によって活性量が上がりオーバードースの危険があります。今回の強化学習モデルはこれらの3要素を表現できているとは言えません。さらに、他のモデルと併用して説明のギャップを埋める際にはそれぞれを別個に用いてモデル化するのではなく、強化学習でアーキテクチャの最適化をしたり、ベイズ統計でハイパーパラメータの調整をしたりするなど、基本的なモデルを色々組み合わせて用いて何らかの精神疾患を数理モデル化できたら面白そう。
おしまい
参考
- 計算論的精神医学
- Pythonで学ぶ強化学習