この記事では、PRML第7章で述べられている、サポートベクターマシン(Support Vector Machine. 以下、SVM)による2値分類を実装します。
対応するjupyter notebookは筆者のgithubリポジトリにあります。連載全体の方針や、PRMLの他のアルゴリズムの実装については、連載のまとめページをご覧いただければと思います。
始めに書いてしまいますが、今回の記事は**長いです。**というのも、「PRMLの本に書いてある内容だといまいち分かった気にならないなー」と思って調べているうちに内容が増えてしまったからです。具体的には、PRMLに記載のない
- 双対問題のきちんとした扱い方
- 双対問題を数値的に解く手法(SMO)の部分
を追加してあります。ということで、この記事を読めば一通りSVMの理論と実装のエッセンスはつかめるのではないかと思います。
なお、理論に興味のない方は、飛ばして2節に進んでしまって大丈夫です(あ、でも1.1と1.2くらいは見ていただいたほうがよいかも。。。)。
それでは、ちょっと長丁場になりますが、始めましょう!
1 理論編1
まずは長い長い理論編です。筆者の理解している範囲でなるべく正確を期して書いてありますが、もし誤りや不正確な点があれば、ご指摘いただけると幸いです。
1.1 設定
最初にも述べたように、2値分類問題を考えます。まず、記号を次のように定義しておきます。
- $N \in \mathbb{N}$ : 訓練データの個数
- $X$ : 入力がとりうる値の集合
- $x_0, x_1, \dots , x_{N-1} \in X$ : 訓練データのうち、入力の部分。
- $t_0, t_1, \dots, t_{N-1} \in \{ -1, 1 \}$ : 訓練データのうち、出力(ラベル)の部分。
1.2 モデルと損失函数
ここでは、予測に用いるモデルと、学習において最小化すべき損失函数を与えます。
1.2.1 モデル
- $M \in \mathbb{N}$ : 特徴量の次元2
- $\phi : X \rightarrow \mathbb{R}^M$ : 入力から特徴量への変換
とします。また、カーネル函数$k : X \times X \rightarrow \mathbb{R}, k(x, x') := \phi(x)^T \phi(x')$は正定値カーネルと仮定します。
2値分類のためのSVMでは、パラメーター$w \in \mathbb{R}^M$(重み)と$b \in \mathbb{R}$(バイアス)が与えられたとき、入力$x$に対して、
$$
\begin{align}
y_{w,b}(x) := w^T \phi(x) + b
\end{align}
$$
を出力します。最終的な予測値としては$\mathrm{sign} [ y_{w,b}(x) ]$を用います。
1.2.2 損失函数と最適化問題
SVMでは、モデルの出力$y(x) \in \mathbb{R}$と正解ラベル$t \in \{ 1, -1 \}$に対して、次の「ヒンジ損失函数」を課します3
$$
\begin{align}
l(y_{w,b}(x), t) = \max \left\{ 0, 1 - t y_{w,b}(x) \right\}
\end{align}
$$
この損失函数の性質や、他の損失函数(0-1損失函数やロジスティック損失函数など)との関係については、杉山将先生の「イラストで学ぶ 機械学習」の8.5節や、こちらの記事をご覧ください。
これに正則化項も付け加えると、SVMの学習においては次の最小化問題を解くことになります4。
$$
\begin{align}
\min_{w \in \mathbb{R}^M, b \in \mathbb{R}}
\left( C \sum_{n=0}^{N-1} \max \left\{ 0, 1 - t_n[w^T \phi(x_n) + b]\right\} + \frac{1}{2}\| w \|^2 \right)
\end{align}
$$
ただし、$C >0$は定数(ハイパーパラメーター)で、正則化の強さをコントロールします。
この損失函数の最小化は、勾配5降下法で解くこともできます。しかし、入力$X$の次元が大きいときには$M$を非常に大きくする必要があります6。従って、この手法では大きい$M$を直接扱う必要があり、計算が困難と考えられます。
この問題を回避するために、次の節ではこの双対問題をLagrange双対問題に変換して解くことにします。
1.3 Lagrange双対問題への変換
Lagrange双対の一般論については、長くなってしまうので、別の記事にしました。必要であれば、適宜そちらをご覧いただければと思います。
1.3.1 主問題の書き換え
まず、maxの部分をslack変数を用いて書き直しておきます7
$$
\begin{align}
& \min_{w \in \mathbb{R}^M, b \in \mathbb{R}, \xi \in \mathbb{R}^N}
\left( C \sum_{n=0}^{N-1} \xi_n + \frac{1}{2}\| w \|^2 \right) \
& s.t. \
& \xi_n \geq 0 \ \ (\forall n \in \{ 0, 1, \dots, N-1 \}),\\
& t_n \left[ w^T \phi(x_n) + b \right] \geq 1 - \xi_n \ \ (\forall n \in \{ 0, 1, \dots, N-1 \}),
\end{align}
$$
後の便宜のために、次のように記号を定義しておきます。
$$
\begin{align}
x &:= (w, b, \xi) \in \mathbb{R}^M \times \mathbb{R} \times \mathbb{R}^N = \mathbb{R}^{N+M+1} \
f(x) &:= C \sum_{n=0}^{N-1} \xi_n + \frac{1}{2} \| w \|^2 \
g_n(x) &:= t_n \left[ w^T \phi(x_n) + b \right] - 1 + \xi_n \
h_n(x) &:= \xi_n \
S &:= \left\{ x \in \mathbb{R}^{N+M+1} \middle |
g_n(x) \geq 0, h_n(x) \geq 0 \ (\forall n \in \{0, \dots, N-1 \}) \right\}
\end{align}
$$
この最適化問題の性質(後で用います)をいくつか挙げておきます:
- 目的函数$f$は凸函数
- 拘束条件を表す函数$g_n$と$h_n$はアファイン函数(従って、凸かつ凹)
- $S$は凸集合であり、内点を持つ
- $f$は$S$上において最小値を持つ
この主問題をLagrange双対問題に変換していきます。
1.3.2 Lagrangian
さきほどの最適化問題に対して、Lagrangian $L : \mathbb{R}^{N+M+1} \times \mathbb{R}_{+}^{2N} \rightarrow \mathbb{R}$は次のように与えられます:
$$
\begin{align}
L(x,\lambda) := f(x) - \sum_{n=0}^{N-1} a_n g_n(x) - \sum_{n=0}^{N-1} \mu_n h_n(x)
\end{align}
$$
ただし、$\lambda = (a,\mu)$と表し、$a,\mu \in \mathbb{R}^{N}_{+}$とします。
1.3.3 双対問題
では、準備が整ったので、双対問題を求めましょう! 1.3.1の最後に述べた性質より、凸最適化問題の強双対定理が利用できます。
双対問題の目的函数$q(\lambda) := \inf_{x \in \mathbb{R}^{N+M+1}} \ L(x, \lambda)$を具体的に求めていきます。そのために、まずは$L$を整理します:
$$
\begin{align}
L(x, \lambda)
&= C \sum_{n=0}^{N-1} {\xi}_{n}
{} + \frac{1}{2} \| w \|^2
{} - \sum_{n=0}^{N-1} a_n \left[ t_n (w^T \phi(x_n) + b) - 1 + \xi_{n} \right]
{} - \sum_{n=0}^{N-1} \mu_n \xi_n \
&= \sum_{n=0}^{N-1}(C - \mu_n - a_n ) \xi_n
{} + \frac{1}{2} | w |^2 - \left[ \sum_{n=0}^{N-1} a_n t_n \phi(x_n) \right]^T w
{} - \sum_{n=0}^{N-1} a_n( b t_n - 1)
\end{align}
$$
ここから、$q$が容易に求められます:
$$
\begin{align}
q(\lambda) = \inf_{x\in\mathbb{R}^{N+M+1}} L(x,\lambda)
= \begin{cases}
\sum_{n=0}^{N-1} a_n - \frac{1}{2} \sum_{n,m=0}^{N-1} a_n a_m t_n t_m k(x_n, x_m)
& (C - \mu_n - a_n = 0 (\forall n \in {0,\dots, N-1 }), \sum_{n=0}^{N-1} a_n t_n = 0) \
-\infty & (\mbox{otherwise})
\end{cases},
\end{align}
$$
ただし、$k(x, x') := \phi(x)^T \phi(x')$です。
これより、$q$は最大値を持つことが示せます。最大値を与える$\lambda$を$\lambda^{\ast} = (a^{\ast}, \mu^{\ast})$と表すことにしましょう。このとき、$a^{\ast} \in [0, C]^{N}$、$\mu^{\ast}_{n} = C - a^{\ast}_{n}$、$\sum_{n=0}^{N-1} a^{\ast}_{n} t_n = 0$が成り立ちます。
ここではいったん、$a^{\ast}$が求まったとし、次に進みます。$a^{\ast}$をどう(数値的に)求めるかについては、1.6節で述べます。
また、後の便宜のため次のように定義しておきます
$$
\begin{align}
\tilde{q}(a) &:= \sum_{n=0}^{N-1} a_n - \frac{1}{2} \sum_{n,m=0}^{N-1} a_n a_m t_n t_m k(x_n, x_m), \
S' &:= \left\{ a \in \mathbb{R}^N \middle| 0 \leq a_n \leq C \ (\forall n = 0, \dots, N-1), \
\sum_{n=0}^{N-1} a_n t_n = 0 \right\}.
\end{align}
$$
1.4 Lagrange双対問題の解から主問題の解へ
ここでは、双対問題の解が$a^{\ast}$が求まったとして、そこから主問題の最適解$x^{\ast} = (w^{\ast}, b^{\ast}, \xi^{\ast})$を求める方法を論じます。
1.4.1 $\xi$
まず、$\xi$については簡単です。
$w^{\ast}$と$b^{\ast}$が求まったとします。このとき、明らかに
$$
\begin{align}
\xi^{\ast}_{n} = \max \left\{ 0, 1 - t_n[{w^{\ast}}^T \phi(x_n) + b^{\ast}] \right\}
\end{align}
$$
が最適解となります。
1.4.2 $w$
凸最適化問題の双対問題についての一般論(別記事の5節参照)より、$x^{\ast}$は
$$
\begin{align}
\forall x \in S : L(x^{\ast}, \lambda^{\ast}) \leq L(x, \lambda^{\ast}),
\end{align}
$$
を満たします。換言すると、$x^{\ast}$は$L(\cdot, \lambda^{\ast})$を最小化する点となります。
このことと、今の問題では$L(x, \lambda^{\ast})$が$\xi, b$に依存しないことより、
$$
\begin{align}
w^{\ast} = \sum_{n=0}^{N-1} a^{\ast}_n t_n \phi(x_n)
\end{align}
$$
が得られます。
1.4.3 $b$
最後に、$b^{\ast}$です。これが一番面倒ですね。。。
PRMLの本では、「$0 < a^{\ast}_{n} < C$を満たす$n$を用いて、(7.36)式から$b^{\ast}$を求められる」とありますが、これは不十分かと思います。というのも、$0 < a^{\ast}_{n} < C$を満たす$n$が存在するとは限らないからです8。
ここでは、そのような場合も対応できる手法を以下の文献の内容に基づいて説明します。
- Bottou, Lin "Support Vector Machine Solvers" https://www.csie.ntu.edu.tw/~cjlin/papers/bottou_lin.pdf
- Chang, Lin "LIBSVM: A Library for Support Vector Machines" https://www.csie.ntu.edu.tw/~cjlin/papers/libsvm.pdf
まず、強双対定理(別記事の5節参照)より、$f(w^{\ast}, b^{\ast}, \xi^{\ast}) = \tilde{q}(a^{\ast})$を満たす$b^{\ast}$を見つければ十分です。
$b^{\ast}$はこの等式を満たす値であればなんでもOKですが、ここではそのような$b^{\ast}$の値を具体的に1つ求める手法を述べます。
まず、両辺の差を次のように表すことができます
$$
\begin{align}
f(w^{\ast}, b^{\ast}, \xi^{\ast}) - \tilde{q}(a^{\ast})
= \sum_{n=0}^{N-1}\left[ C \max \{ 0, g_n(a^{\ast}) - b^{\ast} t_n \} - a^{\ast}_{n} g_n(a^{\ast}) \right]
\end{align}
$$
ただし、
$$
\begin{align}
g_n(a) := \frac{\partial \tilde{q}}{\partial a_n} = 1 - t_n \sum_{m=0}^{N-1} a_m t_m k(x_n, x_m)
\end{align}
$$
は$\tilde{q}$の勾配です。
ここで、$C_n := C \max \{ 0, g_n(a^{\ast}) - b t_n \} - a^{\ast}_{n} g_n(a^{\ast})$と定義しましょう。すると、$\sum_{n=0}^{N-1} C_n = 0$を満たすような$b$を見つけることになります。
maxの中身に着目すると、
$$
\begin{align}
& g_n(a^{\ast}) > bt_n \Longrightarrow C_n = (C- a^{\ast}_{n}) g_n(a^{\ast}) - b C t_n \
& g_n(a^{\ast}) < bt_n \Longrightarrow C_n = - a^{\ast}_{n} g_n(a^{\ast}) \
& g_n(a^{\ast}) = bt_n \Longrightarrow C_n = - a^{\ast}_{n} g_n(a^{\ast}) = - b a^{\ast}_{n} t_n,
\end{align}
$$
が成り立ちます。ここから(やや天下りではありますが)、$C_n = - b a^{\ast}_{n} t_n$なる$b$を見つけることにします。というのも、この関係が成り立てば、$\sum_{n=0}^{N-1} C_n =- b\sum_{n=0}^{N-1}a^{\ast}_n t_n = 0 $となるからです。
そのためには、次のような$b$を見つければ十分であることが分かります
$$
\begin{align}
g_n(a^{\ast}) > b t_n \Longrightarrow a^{\ast}_{n} = C \
g_n(a^{\ast}) < b t_n \Longrightarrow a^{\ast}_{n} = 0
\end{align}
$$
このような$b$が存在することも、きちんと証明できます9。
さらに、この条件は次の等価な条件に書き換えることができます
$$
\begin{align}
n \in I_{up}(a^{\ast}) \Longrightarrow b \geq t_n g_n(a^{\ast}) \
n \in I_{low}(a^{\ast}) \Longrightarrow b \leq t_n g_n(a^{\ast})
\end{align}
$$
ただし、
$$
\begin{align}
I_{up}(a) &:= \left\{n \in \left\{ 0, 1, \dots, N-1 \right\}
\middle| (a_n < C \mbox{ and } t_n = 1) \mbox{ or } (a_n > 0 \mbox{ and } t_n = -1) \right\} \
I_{low}(a) &:= \left\{n \in \left\{ 0, 1, \dots, N-1 \right\}
\middle| (a_n < C \mbox{ and } t_n = -1) \mbox{ or } (a_n > 0 \mbox{ and } t_n = 1) \right\}
\end{align}
$$
以上より、次の条件を満たす$b$を見つければ十分であることが分かります。
$$
\begin{align}
\max_{n \in I_{up}(a^{\ast})} t_n g_n(a^{\ast}) \leq b \leq \min_{n \in I_{low}(a^{\ast})} t_n g_n(a^{\ast})
\end{align}
$$
1.5 予測
パラメーター$w^{\ast}$と$b^{\ast}$が得られれば、入力$x \in X$に対して予測を返すことができます
$$
\begin{align}
\mathrm{sign} \left[ {w^{\ast}}^T \phi(x) + b^{\ast} \right]
= \mathrm{sign} \left[ \sum_{n=0}^{N-1} a^{\ast}_{n} t_n k(x_n, x) + b^{\ast} \right]
\end{align}
$$
このとき、$a^{\ast}_{n} = 0$なる$n$については、予測に効かないことが分かります。対して、予測に効く$x_n$(i.e., $a^{\ast}_{n} \neq 0$なる$n$)はサポートベクターと呼ばれます。
1.6 Lagrange双対問題の数値解法
では、ここまで先延ばしにしてきた、$a^{\ast}$を求める問題をいよいよ考えることにしましょう。残されたタスクは、次の最適化問題の解$a^{\ast}$を求めることでした。
$$
\begin{align}
& \max_{a \in S'} \tilde{q}(a) \
\tilde{q}(a) &:= \sum_{n=0}^{N-1} a_n - \frac{1}{2} \sum_{n,m=0}^{N-1} a_n a_m t_n t_m k(x_n, x_m), \
S' &:= \left\{ a \in \mathbb{R}^N \middle| 0 \leq a_n \leq C \ (\forall n = 0, \dots, N-1), \
\sum_{n=0}^{N-1} a_n t_n = 0 \right\}.
\end{align}
$$
この問題は通常の二次計画問題の手法を用いて解くことができますが、$N$が大きいときは計算が遅くなってしまうことが知られています(が、自分では試していません。。。)。ここでは、$N$が大きいときでも対応できるSMO (Sequential Minimal Optimization)と呼ばれる手法を紹介します。
SMOでは、一度の変数更新で、2つの変数(working setと呼びます)のみを更新します。この節では、
- 初期値
- 更新の停止基準
- 更新する変数をどう選ぶか
- 更新式の具体的な形
について述べていきます。また、ここでの計算を通じて$b^{\ast}$の値を求める手法についても述べます。なお、ここでのSMOの定式化は、上述の Bottou, Lin "Support Vector Machine Solvers" https://www.csie.ntu.edu.tw/~cjlin/papers/bottou_lin.pdf に従います。
1.6.1 初期化
SMOも変数を繰り返し更新する手法なので、初期値が必要になります。今回考えている問題は凸最適化問題なので、理想的には初期値はなんでもよいのですが、ここでは簡単のために$a=0$とおくことにします。
1.6.2 停止基準
次に、いつ更新をやめるかを判断するための停止基準について考えましょう。
ここでは、次のKKT条件を変形して、停止基準として用いることにします。
$$
\begin{align}
\exists \alpha = (\alpha_0, \dots, \alpha_{N-1}) \in \mathbb{R}_{+}^{N}, \
\exists \beta = (\beta_0, \dots, \beta_{N-1}) \in \mathbb{R}_{+}^{N}, \
\exists \gamma \in \mathbb{R}, \
\forall n \in \left\{ 0, 1, \dots, N-1 \right\} \ : \
\begin{cases}
g_n(a) + \alpha_n - \beta_n - \gamma t_n = 0 \
\alpha_n a_n = 0 \
\beta_n (C - a_n) = 0
\end{cases}
\end{align}
$$
上記のKKT条件は、上手く変形すると次の条件に書き換えることができます10。
$$
\begin{align}
\max_{n \in I_{up}(a)} t_n g_n(a) \leq \min_{n \in I_{low}(a)} t_n g_n(a),
\end{align}
$$
ただし、$I_{up}$は$I_{low}$は1.4.3節で定義した集合です。
1.6.3 Working setの選択
次に、working set(一度のupdateで更新する2つの変数)を選ぶ手法について述べます。
選び方には様々なものがありますが11、ここではmaximal violating pairを選ぶという手法をとることにします。
この手法では、更新すべき変数の添字$i, j$を次のように選びます:
$$
\begin{align}
i &= \mathrm{argmax}_{i' \in I_{up}(a)} t_{i'} g_{i'}(a) \
j &= \mathrm{argmin}_{j' \in I_{low}(a)} t_{j'} g_{j'}(a)
\end{align}
$$
言い換えると、停止基準を最も大きく破る$i, j$のペアを選ぶことにします。
$i, j$の定義と停止基準から分かるように、$t_{i} g_{i}(a) \leq t_{j} g_{j}(a)$であれば繰り返しを終了し、$t_{i} g_{i}(a) > t_{j} g_{j}(a)$であれば変数の更新を行います。
また、1.4.3節での$b^{\ast}$の満たす十分条件を思い出すと、繰り返しを終了した際には、$b^{\ast}$を$t_i g_i(a)$と$t_j g_j(a)$の間の値にとれば良いことがわかります。ここではひとまず、$b^{\ast} = \frac{t_i g_i(a) + t_j g_j(a)}{2}$とすることにしましょう。
1.6.4 更新式
では、いよいよ変数の更新です。今、前のステップでの$a$の値が得られ、これに対してworking set $i, j$が選択されているとします。また、停止基準を満たさなかったとしましょう。このとき、次の更新後の$a$(これを$a^{new}$とします)を表す式を得るのがこの節の目的です。加えて、$g$の値も保持しておくことにし、この更新式も与えます12。なお、今まで$g$は(aを引数に取る)函数として表してきましたが、今後はベクトルの値を表すものとします。
1.6.4.1 $a$の更新式
まず、変数$a$の更新式を考えます。
先ほども述べたように、SMOにおける更新では、(working setが$i, j$のとき)変数$a_i$と$a_j$のみを動かせる場合の$\tilde{q}$の最大化問題を解きます。
最初に結果を与えておくと、更新式は
$$
\begin{align}
& a^{new}_{n} =
\begin{cases}
a_{i} + \lambda t_i & (n = i) \
a_{j} - \lambda t_j & (n = j) \
a_{n} & (\mbox{otherwise})
\end{cases} \
& \lambda := \min \left\{ A_i, B_j , \frac{t_i g_i - t_j g_j}{K_{i,i} - 2 K_{i,j} + K_{j,j}} \right\} \
& A_i := \begin{cases}
C - a_i & (t_i = 1) \
a_i & (t_i = -1)
\end{cases} \
& B_j := \begin{cases}
a_j & (t_j = 1) \
C - a_j & (t_j = -1)
\end{cases} \
& K_{n, m} := k(x_n, x_m)
\end{align}
$$
となります。
この導出の概要をざっくりと述べておきましょう。
まず、今動かせるのは第$i, j$成分のみなので、$a^{new}$を次のように表します。
$$
\begin{align}
a^{new}_{n} = a_n + \delta_{n, i} t_i d_i + \delta_{n, j} t_j d_j,
\end{align}
$$
ここで、$\delta_{n,m}$はKronecker deltaで、$d_i$と$d_j$は$a^{new}$と$a$の差(に$t_i, t_j$をかけたもの)を表す新しい変数です。
これを用いて、最大化問題を$d_i, d_j$を用いて表すことにします:
$$
\begin{align}
& \max_{d_i , d_j} \tilde{q}(a^{new}) \
& s.t. \
& d_i + d_j = 0 \
& - a_i \leq t_i d_i \leq C - a_i \
& - a_j \leq t_j d_j \leq C - a_j
\end{align}
$$
特に、$\tilde{q}(a^{new})$は次のように簡潔に表すことができます:
$$
\begin{align}
\tilde{q}(a^{new})
= \tilde{q}(a) + \left( t_i g_i \ t_j g_j\right)
\begin{pmatrix}
d_i \
d_j
\end{pmatrix}
- \frac{1}{2} \left( K_{i,i} d_{i}^{2} + 2 K_{i,j}d_i d_j + K_{j,j}d_{j}^{2} \right)
\end{align}
$$
更に、第一の拘束条件を用いると、この最適化問題は1変数の問題に帰着します:
$$
\begin{align}
& \max_{d_i \in \mathbb{R}} -\frac{1}{2}\left( K_{i,i} - 2 K_{i,j} + K_{j,j} \right) d_{i}^{2} + (t_i g_i - t_j g_j)d_i \
& s.t. \
& - a_i \leq t_i d_i \leq C - a_i \
& - a_j \leq -t_j d_i \leq C - a_j
\end{align}
$$
$K_{i,i} - 2 K_{i,j} + K_{j,j} > 0$であること13と、$t_i g_i - t_j g_j > 0$であること14より、この最大化問題の解が$d_i = \lambda$であることが示せます。
2.5.4.2 Update of the gradient
勾配の値$g$の更新式は、$a$の更新式よりただちに従います:
$$
\begin{align}
g^{new}_{n} = g_n - \lambda t_n (K_{n, i} - K_{n, j})
\end{align}
$$
2 数式からコードへ
理論編は終了して、これからいよいよコードを書いていきます。理論編を読んでくださった方、お疲れ様でした! 理論編をすっとばした方、大丈夫です。必要な結果だけを2.1にさらっとまとめてありますので、ご覧くださいませ。
2.1 理論のおさらい
1節で述べた話のうち、コードを書くのに必要な結果だけをまとめておきます。
-
正則化定数$C$を与えます。
-
カーネル行列$(K_{n,m})_{n,m=0,1, \dots, N-1}$ (ただし、$K_{n,m} = k(x_n, x_m)$)を求める函数を与えます。$k$は正定値カーネル函数とします。
-
分類器に訓練データ$X$と$t$を与えます。
-
次の擬似コードで表されるSMO algorithmを用いて$a, b$を求めます。
- $\forall n \in \{ 0,1, \dots, N-1 \}$ $a_n \leftarrow 0$
- $\forall n \in \{ 0,1, \dots, N-1 \}$ $g_n \leftarrow 1$
- while True:
- $\hspace{1cm}$ $I_{up}\leftarrow \left\{n \in \left\{ 0, 1, \dots, N-1 \right\}
\middle| (a_n < C \mbox{ and } t_n = 1) \mbox{ or } (a_n > 0 \mbox{ and } t_n = -1) \right\}$ - $\hspace{1cm}$ $I_{low} \leftarrow \left\{n \in \left\{ 0, 1, \dots, N-1 \right\}
\middle| (a_n < C \mbox{ and } t_n = -1) \mbox{ or } (a_n > 0 \mbox{ and } t_n = 1) \right\}$ - $\hspace{1cm}$ $i \leftarrow \mathrm{argmax}_{n \in I_{up}}t_n g_n$
- $\hspace{1cm}$ $j \leftarrow \mathrm{argmin}_{n \in I_{low}}t_n g_n$
- $\hspace{1cm}$ if $t_i g_i \leq t_j g_j$:
- $\hspace{2cm}$ $b \leftarrow (t_i g_i + t_j g_j)/2 $
- $\hspace{2cm}$ break
- $\hspace{1cm}$ else:
- $\hspace{2cm}$ $A \leftarrow C - a_i $ if $t_i == 1$ else $a_i$
- $\hspace{2cm}$ $B \leftarrow a_j$ if $t_j == 1$ else $C - a_j$
- $\hspace{2cm}$ $\lambda \leftarrow \min \left\{ A, B, \frac{t_i g_i - t_j g_j}{K_{i,i} - 2 K_{i,j} + K_{j,j} }\right\} $
- $\hspace{2cm}$ $a_i \leftarrow a_i + \lambda t_i $
- $\hspace{2cm}$ $a_j \leftarrow a_j - \lambda t_j $
- $\hspace{2cm}$ $\forall n \in { 0,1, \dots, N-1 }$ $g_n \leftarrow g_n - \lambda t_n (K_{n, i} - K_{n, j})$
-
求めた$a$ and $b$を用いて、与えられた入力$x$に対して予測を次のように返します
$$
\begin{align}
\mathrm{sign} \left[ \sum_{n=0}^{N-1} a_{n} t_n k(x_n, x) + b \right]
\end{align}
$$
2.2 実装上のtips
あとは上記の擬似コードを翻訳するだけ...と行きたいところですが、ちょっと一工夫しておきます。
というのも、上の擬似コードでは収束判定や$I_{up}$, $I_{low}$の定義において不等号を用いているのですが、数値誤差が含まれる場合はこのままだと必ずしも上手くいかない可能性があるからです。そこで、以下のような変更を加えます。
- 十分小さい$\varepsilon>0$を用いて、収束判定の条件を$t_i g_i \leq t_j g_j$から$t_i g_i \leq t_j g_j + \varepsilon$, where $\varepsilon > 0$に変更します。
- 十分小さい$\delta > 0$を用いて、$I_{up}, I_{low}$の定義を$I_{up}\leftarrow \left\{n \in \left\{ 0, 1, \dots, N-1 \right\} \middle| (a_n < C - \delta \mbox{ and } t_n = 1) \mbox{ or } (a_n > \delta \mbox{ and } t_n = -1) \right\}$のように変更します($I_{low}$も同様です。)。
なお、実験したところ、$\varepsilon = 0$とすると収束まで大幅に時間がかかりました。対して、$\delta = 0$としてもあまり影響は大きくないようでした。ただし、あまり多くの場合に対して試したわけではないので、確たることは言えません。
2.3 Kernel
では、いよいよコードを書いていきましょう!
まずはkernel行列の計算を行うobjectを与えておきます。この実装では、線型kernel
$$
\begin{align}
k(x, x') = x^T x'
\end{align}
$$
とGaussian kernel
$$
\begin{align}
k(x,x') = \exp \left( -\frac{\|x - x' \|^2}{2s^2} \right)
\end{align}
$$
を用います。
この記事の実装では、前回のガウス過程回帰で用いたkernelオブジェクトを参考に実装します。ポイントは以下の通りです。
- kernelのパラメーターは
thetaで保持しておきます。 -
__call__でkernel函数の値を計算します。ただし、kernel(X, Y)の両引数が複数のデータ点を表す場合は戻り値は2次元配列、片方のみが複数のデータ点を表す場合は戻り値は1次元配列、両引数がそれぞれ1つのデータ点を表す場合は戻り値はfloatとします。これは、SMOと予測のときにkernelをラクに利用するための仕様です。
では、まずは線型kernelです。
class LinearKernel:
def __init__(self, theta=None):
pass
def __call__(self, X, Y):
'''
This method calculates kernel matrix, or a single scalar, or a vector, depending on the input.
The kernel function is assumed to be the linear kernel function
Parameters
----------
X, Y : 2-D numpy array, or 1-D numpy array
numpy array representing input points.
If X (resp. Y) is a 2-D numpy array, X[n, i] (resp. Y[n, i]) represents the i-th element of n-th point in X (resp Y).
If X (resp. Y) is a 1-D numpy array, it is understood that it represents one point, where X[i] (resp Y[i]) reprensets the i-th element of the point.
Returns
----------
K : numpy array
If both X and Y are both 2-D numpy array, K is a 2-D numpy array, with shape = (len(X), len(Y)), and K[i, j] stands for k(X[i], Y[j]).
If X is a 2-D numpy array and Y is a 1-D numpy array, K is a 1-D numpy array, where
'''
return X @ Y.T
次に、Gaussian kernel
class GaussianKernel:
def __init__(self, theta):
self.theta = theta
def __call__(self, X, Y):
'''
This method calculates kernel matrix, or a single scalar, or a vector, depending on the input.
The kernel function is assumed to be the Gaussian kernel function
Parameters
----------
X, Y : 2-D numpy array, or 1-D numpy array
numpy array representing input points.
If X (resp. Y) is a 2-D numpy array, X[n, i] (resp. Y[n, i]) represents the i-th element of n-th point in X (resp Y).
If X (resp. Y) is a 1-D numpy array, it is understood that it represents one point, where X[i] (resp Y[i]) reprensets the i-th element of the point.
Returns
----------
K : numpy array
If both X and Y are both 2-D numpy array, K is a 2-D numpy array, with shape = (len(X), len(Y)), and K[i, j] stands for k(X[i], Y[j]).
If X is a 2-D numpy array and Y is a 1-D numpy array, K is a 1-D numpy array, where
'''
if (X.ndim == 1) and (Y.ndim == 1):
tmp = np.linalg.norm(X - Y)**2
elif ((X.ndim == 1) and (Y.ndim != 1)) or ((X.ndim != 1) and (Y.ndim == 1)):
tmp = np.linalg.norm(X - Y, axis=1)**2
else:
tmp = np.reshape(np.sum(X**2,axis=1), (len(X), 1)) + np.sum(Y**2, axis=1) -2 * (X @ Y.T)
K = np.exp(- tmp/(2*self.theta**2))
return K
2.3 分類器
では、ついにSVM分類器本体SVCクラスを定義します。
SVCクラスのオブジェクトには、以下のデータ属性を持たせることにします:
-
C: 正則化定数の逆数 -
kernel: SVMが用いるKernel函数を表すオブジェクト -
X_sv: サポートベクター。 -
t_sv: サポートベクターに対応するラベル。 -
a: 双対問題の解のうち、非零の部分(サポートベクターに対応するもの)。 -
b: バイアス
また、次のメソッドを持たせることにします。
-
fit: SMOアルゴリズムを用いてフィッティングを行うメソッド。これによりaとbの値を決めます。 -
decision_function: 与えられた入力に対し、決定函数を返すメソッド。 -
predict: 与えられた入力に対し、予測されるラベルを返すメソッド。
これを実装したのが、次のコードです。tol_convが2.2節の$\varepsilon$、tol_svが2.2節の$\delta$に対応しています。
また、maximal violating pair i, jを選ぶ部分がちょっとややこしいですが、基本的には定義を忠実にコードに直したものになっています15。
class SVC:
def __init__(self, kernel, C=1.0):
self.C = C
self.kernel = kernel
def fit(self, X, t, tol_conv=1e-6, tol_sv=1e-9, show_time = False):
'''
This method fits the classifier to the training data
Parameters
----------
X : 2-D numpy array
Array representing training input data, with X[n, i] being the i-th element of n-th point in X.
t : 1-D numpy array
Array representing training label data. Each component should be either 1 or -1
tol_conv : float
Tolerance for numerical error when judging the convergence.
tol_sv : float
Tolerance for numerical error when judging the support vectors.
show_time : boolean
If True, training time and the number of iteration is shown.
'''
N = len(t)
a = np.zeros(N)
g = np.ones(N)
nit = 0
time_start = time.time()
while True:
vals = t*g
i = np.argmax([ vals[n] if ( (a[n] < self.C - tol_sv and t[n]==1) or (a[n] > tol_sv and t[n]==-1)) else -float("inf") for n in range(N) ])
j = np.argmin([ vals[n] if ( (a[n] < self.C - tol_sv and t[n]==-1) or (a[n] > tol_sv and t[n]==1)) else float("inf") for n in range(N) ] )
if vals[i] <= vals[j] + tol_conv:
self.b = (vals[i] + vals[j])/2
break
else:
A = self.C - a[i] if t[i] == 1 else a[i]
B = a[j] if t[j] == 1 else self.C - a[j]
lam = min(A, B, (t[i]*g[i] - t[j]*g[j])/(self.kernel(X[i], X[i]) - 2*self.kernel(X[i], X[j]) + self.kernel(X[j], X[j])) )
a[i] = a[i] + lam*t[i]
a[j] = a[j] - lam*t[j]
g = g - lam*t*( self.kernel(X, X[i]) - self.kernel(X, X[j]) )
nit += 1
time_end = time.time()
if show_time:
print(f"The number of iteration : {nit}")
print(f"Learning time : {time_end-time_start} seconds")
ind_sv = np.where( a > tol_sv)
self.a = a[ind_sv]
self.X_sv = X[ind_sv]
self.t_sv = t[ind_sv]
def decision_function(self, X):
'''
This method returns the value of the decision function for the given input X.
Parameters
----------
X : 2-D numpy array
Array representing input data, with X[n, i] being the i-th element of n-th point in X.
Returns
----------
val_dec_func : 1-D numpy array
Array representing the value of the decision function
'''
val_dec_func = self.kernel(X, self.X_sv) @ (self.a*self.t_sv) + self.b
return val_dec_func
def predict(self,X):
'''
This method returns the predicted label for the given input X.
Parameters
----------
X : 2-D numpy array
Array representing input data, with X[n, i] being the i-th element of n-th point in X.
Returns
----------
pred : 1-D numpy array
Array representing the predicted label
'''
pred = np.sign(self.decision_function(X))
return pred
3. 実験
さーて、とうとう実験ができるところまでたどり着きました!
3.1 データ
データとしては、make_moonsで作った、次の2次元toy dataを利用します。
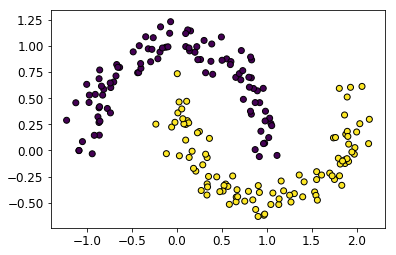
データ点の個数は200としてあります。
3.2 カーネル函数への依存性
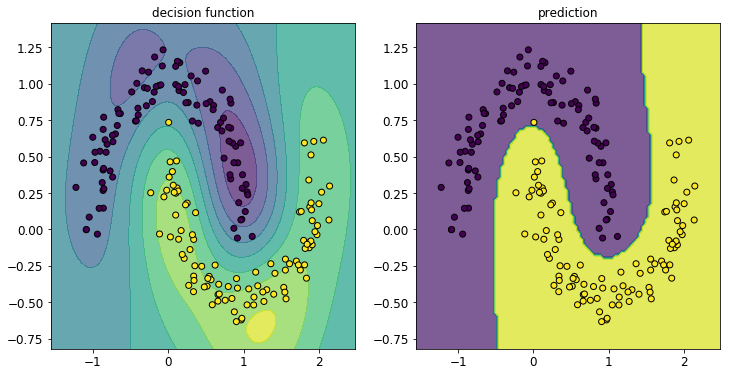
まず、線型カーネルとガウシアンカーネルでそれぞれさくっとSVMによる分類を行った結果を図で見てみましょう。図の左側は決定函数、右側は予測するラベルをcontourfでプロットしています。
まずは線型カーネル。
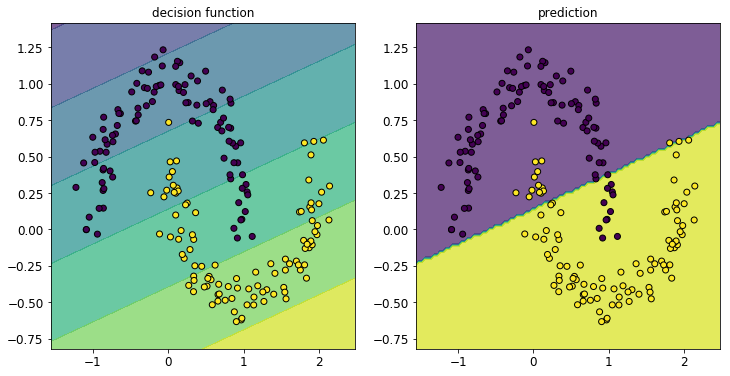
モデルの定義からも明らかに、決定境界は直線になります。ということでお、このデータに線型カーネルはあまり適していませんでしたね...。ちなみに、この問題で線型カーネルを使う場合は、わざわざ双対問題に直して解くご利益はあまりないかと思います(直接勾配法で解けば良いのではないかと。。。1.2.2節の終わり参照。)。
良い感じに曲がった決定境界を描き、精度良く分類できていますね! これも、線型でないカーネル函数を用いたおかげです。双対問題に直して解く手法のありがたさが分かるのではないかと思います。
3.2 疎性の確認
さて、SVMの(ガウス過程などと比べたときの)利点の1つに、「解が疎になる」ということが挙げられました。これがPRML7章のタイトルにもなっているくらいですし、PRMLも推している性質でしょう。ということで、本当に解が疎になっているか、確認しておきましょう。
具体的には、先ほどの図にサポートベクターを別にプロットしておきましょう。通常の訓練データ点を丸で、サポートベクターを四角でプロットしたのが、次の図です:
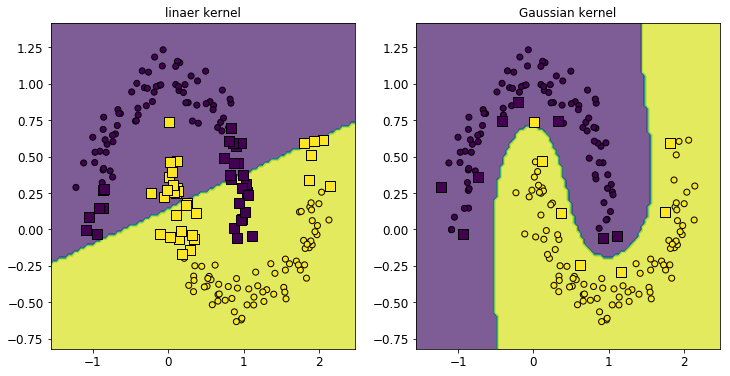
いずれの場合も、サポートベクターの個数は訓練データ全体の個数に比べて大幅に小さくなっていることが見て取れます。特にガウシアンカーネルの場合、サポートベクターは元の訓練データの1割以下となっていました。
これにより、メモリの節約と予測の高速化ができそうなことが理解できるかと思います16。
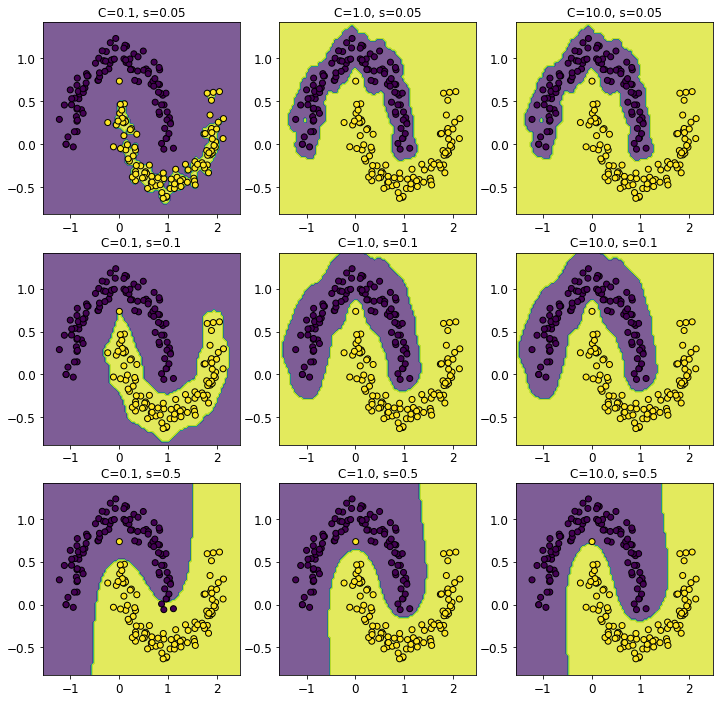
3.3 ハイパーパラメーターの影響
最後に、ガウシンカーネルの場合について、ハイパーパラメーター$C$と$s$の影響を見ておきましょう。直感的には、$C$は大きいほど正則化が弱くなり、$s$は大きくなるほどカーネルの空間スケールが大きくなるはずです。で、試してみた結果は以下の通り:
やはり、
- $s$を大きくするほど決定境界がな滑らかになる
- $C$を大きくするほど訓練データの誤分類が減る
ことが見て取れます。
4 まとめ
この記事では、サポートベクターマシン(support vector machine, SVM)による2値分類を実装しました。PRMLに記載の内容だけでは満足できなかったため、双対問題の正確な扱い方や、SMOによる双対問題の数値解法についても詳しく述べました。
ただ、せっかく「大きなデータに対しては普通に2次計画法で解くと時間がかかる」「解が疎になるので、訓練データが大きいときでも予測が楽になる」などと書いた割には大きなデータが扱えていないので、いずれは大きいデータを扱ってパフォーマンスの差も確認したいと考えています。
長い記事になっていましたが、最後まで読んでくださってありがとうございました!
-
いつもは「理論のおさらい」ですが、今回はPRMLの本に載っていない内容が主なので、「おさらい」は省きました。 ↩
-
ここでは特徴量の次元は有限とします。後でGauss kernelを用いる場合は特徴量の次元が無限の場合を考えることになるので、この記事の議論は厳密には成り立ちません。恐らく、(次元が有限とは限らない)Hilbert空間上へと最適化問題とそのLagrange双対の理論を拡張すればほぼそのままの議論が成り立つとは思います。ただ、筆者にはやや荷が重いかと思い、手をつけていません。。。 ↩
-
SVMはマージン最大化から導入することもできますが、ヒンジ損失函数を用いるほうが簡潔に済むので、今回はこちらを用いました。 ↩
-
細かいけど数学的には大事な話:この最適化問題はきちんと最小解を持つことが証明できます。証明はやや面倒ですが、「変数$w, b$のノルムが十分大きいと、目的函数が無限大に発散する」ことと、目的函数が連続であることを示せば証明できます。 ↩
-
正確には、損失函数が微分不可能なので劣勾配。 ↩
-
具体的には、3章についての記事でも書いたように、$X=\mathbb{R}^d$のとき、$M$は$d$に対して指数的に大きくする必要があります。 ↩
-
これにより、max記号がなくなり、後の変換がラクになります(slack変数を用いなかったらどうなるかは詳しくはやっていませんが。。。)。 ↩
-
たとえば、$N=2$, $X=\mathbb{R}^2$, $x_0 = (1,0)^T, x_1 =(0,1)^T$, $t_0=1, t_1 = -1$, $k(x,x')=x^T x'$, $C=1/2$とすれば、$a^{\ast}_{n} = C$が全ての$n$で成り立ちます。 ↩
-
$a^{\ast}$が$\tilde{q}$を$S'$上で最大化し、従って対応するKKT条件を満たすことから証明できます。 ↩
-
$\alpha_n$ and $\beta_n$が非負であることと、相補性条件$\alpha_n a_n = 0$ and $\beta_n (C - a_n) = 0$を用い、$g_n(a) - \gamma t_n$の符号に着目すれば導出することができます。 ↩
-
実はランダムでも良いそうです(「機械学習のための連続最適化」14.2.1節から孫引き。)。 ↩
-
$g$は停止判定やworking setの選択で用います。これを毎回定義に従って計算すると、$\mathcal{O}(N^2)$の計算時間がかかってしまい、非効率的です。 ↩
-
$K$が正定値であることより従います。 ↩
-
$i,j$はmaximal violating pairであり、今は変数の更新を行っていることより従います。 ↩
-
infを人手で入れてる辺りエレガントでないので、もっと良いやり方がないか思案中。。。 ↩ -
きちんと大規模なデータでは試していないので、これによる予測の高速化がどの程度のものなのかは自信がありません。 ↩