文書の表現学習は文書の検索や分類タスクにおいて重要であり,これまでLDAのような生成モデルを用いた手法が提案されてきました.
ここではニューラルネットワークによる生成モデルと,それらを使った文書の表現学習についてまとめました.
ニューラル生成モデル
生成モデルとは観測データ$\boldsymbol{x}$が従う確率分布$p(\boldsymbol{x})$を表すモデルです.
生成モデルの推論では観測データを使って学習モデルを調整して真の生成モデルの近似を行います.
以下では学習モデルとしてニューラルネットを用いた例を紹介します.
ボルツマンマシン
ボルツマンマシンは2値の確率変数($x \in \{0, 1\}$)をノードとする無向グラフの結合により表される生成モデルです.
以下のようなエネルギー関数を定義し,これを正規化して確率を表します(モデルのパラメータをまとめて$\boldsymbol{\Theta}$とします).
\begin{align}
E(\boldsymbol{x}; \boldsymbol{\Theta})
& = - \boldsymbol{x}^\mathrm{T}\boldsymbol{Wx} - \boldsymbol{b}^\boldsymbol{T}\boldsymbol{x}\\
p(\boldsymbol{x}|\boldsymbol{\Theta})
& =
\frac{1}{\mathcal{Z}(\boldsymbol{\theta})}
\exp\left(-E(\boldsymbol{x};\boldsymbol{\Theta})\right)\\
\mathcal{Z}(\boldsymbol{\Theta})
& =
\sum_\boldsymbol{x}\exp\left(-E(\boldsymbol{x};\boldsymbol{\Theta})\right)
\end{align}
$\mathcal{Z}(\boldsymbol{\Theta})$は分配関数とよばれ,$\sum_\boldsymbol{x}$は$\boldsymbol{x}$の可能な実現値のすべての組み合わせに関する総和を表します.
制限ボルツマンマシン
制限ボルツマンマシンは完全2部グラフの2層構造をもち,一方は観測可能な可視変数$\boldsymbol{v}$,もう一方は隠れ変数$\boldsymbol{h}$で構成されます.
エネルギー関数と確率は次のようになります.
\begin{align}
E(\boldsymbol{v}, \boldsymbol{h};\boldsymbol{\Theta})
& = - \boldsymbol{h}^\mathrm{T}\boldsymbol{Wv} - \boldsymbol{b}^\boldsymbol{T}\boldsymbol{v} - \boldsymbol{a}^\boldsymbol{T}\boldsymbol{h}\\
p(\boldsymbol{v}, \boldsymbol{h}|\boldsymbol{\Theta})
& =
\frac{1}{\mathcal{Z}(\boldsymbol{\theta})}
\exp\left(-E(\boldsymbol{v}, \boldsymbol{h};\boldsymbol{\Theta})\right)\\
\mathcal{Z}(\boldsymbol{\Theta})
& =
\sum_\boldsymbol{v,h}\exp\left(-E(\boldsymbol{v}, \boldsymbol{h};\boldsymbol{\Theta})\right)
\end{align}
可視変数$\boldsymbol{v}$に関する確率は$p(\boldsymbol{v}, \boldsymbol{h}|\boldsymbol{\theta})$を隠れ変数$\boldsymbol{h}$について周辺化して,
p(\boldsymbol{v}|\boldsymbol{\theta})
= \sum_\boldsymbol{h}p(\boldsymbol{v}, \boldsymbol{h}|\boldsymbol{\theta})
となります.
RBMの特徴は各層内の変数は互いに独立であることです.
一方の層は他方の層が与えられた下での条件付き独立性を持ち,条件付き確率は
\begin{align}
p(h_i=1|\boldsymbol{v}, \boldsymbol{\theta})
& =
\frac{p(h_i, \boldsymbol{v}|\boldsymbol{\theta})}{p(\boldsymbol{v}|\boldsymbol{\theta})}
= \sigma(\boldsymbol{W}_{i,:}\boldsymbol{v} + a_i)\\
p(v_j=1|\boldsymbol{h}, \boldsymbol{\theta})
& =
\frac{p(v_j,\boldsymbol{h}|\boldsymbol{\theta})}{p(\boldsymbol{h}|\boldsymbol{\theta})}
= \sigma(\boldsymbol{W}_{:,j}^\mathrm{T}\boldsymbol{h} + b_j)\\
\end{align}
と表されます.
この独立性により各層ごとにギブスサンプリングを行うことができます.
パラメータの学習はデータセットを${\boldsymbol{v}^{(n)}}_{n=1}^N$として以下の対数尤度関数を勾配上昇法により行います.
\begin{align}
\mathcal{L}
& = \ln\left(
\prod_{n=1}^Np(\boldsymbol{v}^{(n)}|\boldsymbol{\theta})
\right)\\
\end{align}
対数尤度の各パラメータに対する微分は次の式になります.
\begin{align}
\frac{\partial\mathcal{L}}{\partial W_{ij}}
& = \sum_{n=1}^N v_j^{(n)}p(h_i|\boldsymbol{v}^{(n)},\boldsymbol{\Theta}) -
N\mathbb{E}_{p_{model}}[v_jh_i]\\
\frac{\partial\mathcal{L}}{\partial b_j}
& = \sum_{n=1}^N v_j^{(n)} - N
\mathbb{E}_{p_{model}}[v_j]\\
\frac{\partial\mathcal{L}}{\partial a_i}
& = \sum_{n=1}^N p(h_i|\boldsymbol{v}^{(n)},\boldsymbol{\Theta}) -
N\mathbb{E}_{p_{model}}[h_i]\\
\end{align}
ここで$\mathbb{E}_{p model}[\cdot]$はモデルの確率変数について可能なすべての実現値を評価する必要があり,解析的に解くことはできません.
RBMの学習ではこの期待値を少ないギブスサンプリング回数で近似を行うコントラスティブ・ダイバージェンス法(CD法)を用いて計算します.
VAE
潜在変数を用いた生成モデルは以下のようにデータ$\boldsymbol{x}$と潜在変数$\boldsymbol{z}$の同時確率を潜在変数$\boldsymbol{z}$について周辺化して求めます.
p(\boldsymbol{x}) = \int p(\boldsymbol{x}|\boldsymbol{z})p(\boldsymbol{z})\mathrm{d}\boldsymbol{z}
積分計算が困難で$p(\boldsymbol{x})$が解析的に求まらない場合は$p(\boldsymbol{z})$からサプリングした標本点 $\{\boldsymbol{z}_i\}$ を使って
p(\boldsymbol{x}) \approx
\frac{1}{N}\sum_{i=1}^{N}p(\boldsymbol{x}|\boldsymbol{z}_i)
のように近似をおこないます.
VAEでは$\boldsymbol{x}$を生成するような$\boldsymbol{z}$をサンプリングするために$q(\boldsymbol{z}|\boldsymbol{x})$という関数を考えます.
学習のために事後分布$p(\boldsymbol{z}|\boldsymbol{x})$とのKL距離を考えます.
\begin{align}
\mathcal{D}_{KL}[q(\boldsymbol{z}|\boldsymbol{x})\|p(\boldsymbol{z}|\boldsymbol{x})]
& =
\mathbb{E}_{z\sim q}[\ln q(\boldsymbol{z}|\boldsymbol{x}) - \ln p(\boldsymbol{z}|\boldsymbol{x})] \\
& =
\mathbb{E}_{z\sim q}[\ln q(\boldsymbol{z}|\boldsymbol{x}) - \ln p(\boldsymbol{x}|\boldsymbol{z}) - \ln p(\boldsymbol{z}) ] + \ln p(\boldsymbol{x}) \\
& =
\mathcal{D}_{KL}[q(\boldsymbol{z}|\boldsymbol{x})\| p(\boldsymbol{z})] - \mathbb{E}_{z\sim q}[\ln p(\boldsymbol{x}|\boldsymbol{z})] + \ln p(\boldsymbol{x})
\end{align}
KL距離は非負なので,
\ln p(\boldsymbol{x}) \geq \mathbb{E}_{z\sim q}[\ln p(\boldsymbol{x}|\boldsymbol{z})] - \mathcal{D}_{KL}[q(\boldsymbol{z}|\boldsymbol{x})\| p(\boldsymbol{z})]
が成り立ちます.学習ではこの右辺を最大化します.
ここで,各確率分布について以下のような正規分布を仮定します.
\begin{align}
\boldsymbol{\mu}, \boldsymbol{\Sigma}
& = f_{encoder}(\boldsymbol{x};\boldsymbol{\theta}_{encoder}) \\
q(\boldsymbol{z}|\boldsymbol{x})
& =
\mathcal{N}(\boldsymbol{z}|\boldsymbol{\mu}, \boldsymbol{\Sigma})\\
p(\boldsymbol{x}|\boldsymbol{z})
& =
\mathcal{N}(\boldsymbol{x}|f_{decoder}(\boldsymbol{z}), \sigma^2\boldsymbol{I})\\
p(\boldsymbol{z})
& =
\mathcal{N}(\boldsymbol{z}|\boldsymbol{0}, \boldsymbol{I})
\end{align}
すると$\ln p(\boldsymbol{x}|\boldsymbol{z})= const. -\frac{1}{2\sigma^2}||\boldsymbol{x} - f(\boldsymbol{z})||^2$が成り立ちます.
$\mathbb{E}_{z\sim q}[\ln p(\boldsymbol{x}|\boldsymbol{z})]$ はサンプリングによる近似を行うと
\mathbb{E}_{z\sim q}[\ln p(\boldsymbol{x}|\boldsymbol{z})] \approx \frac{1}{L}\sum_{l=1}^L\ln p(\boldsymbol{x}|\boldsymbol{z}^{(l)})
となり,以下の損失関数が求まります.
\begin{align}
\min_{\boldsymbol{\theta}_{encoder},\boldsymbol{\theta}_{decoder}}\frac{1}{N}\sum_{n=1}^N\frac{1}{2L}\sum_{l=1}^L\|\boldsymbol{x}^{(n)} &- f_{decoder}(\boldsymbol{z}^{(n, l)})\|^2 + \mathcal{D}_{KL}[\mathcal{N}(\boldsymbol{z}|\mu^{(n)}, \Sigma^{(n)})\| \mathcal{N}(\boldsymbol{z}|\boldsymbol{0}, \boldsymbol{I})]\\
&\boldsymbol{\mu}^{(n)}, \boldsymbol{\Sigma}^{(n)} = f_{encoder}(\boldsymbol{x}^{(n)})\\
& \boldsymbol{z}^{(n)} \sim \mathcal{N}(\boldsymbol{z}|\boldsymbol{\mu}^{(n)}, \boldsymbol{\Sigma}^{(n)})
\end{align}
これを最小化すると$\ln p(\boldsymbol{x})$の下界を最大化することがわかります.
第1項はデータの再構築に関する損失,第2項は$\boldsymbol{z}$の事後分布とエンコーダの分布に関する損失を表しています.
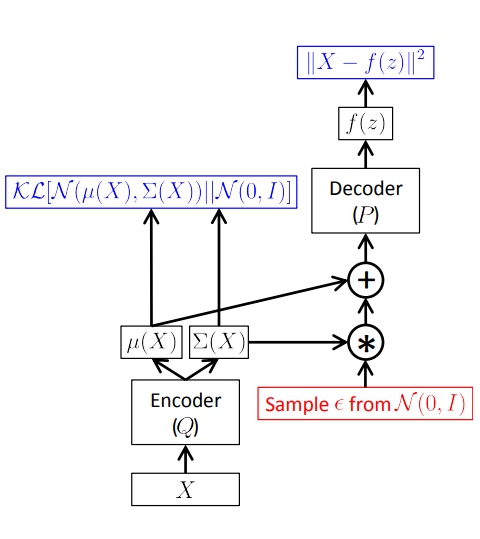
(引用: Tutorial on Variational Autoencoders)
$\boldsymbol{z}$をサンプリングする際は以下に示すreparameterization trickと呼ばれる手法を使うことで,逆伝搬のときに再構築誤差を$f_{encoder}(\boldsymbol{x})$に伝えることができます.
\begin{align}
\epsilon & \sim \mathcal{N}(\boldsymbol{0}, \boldsymbol{I}) \\
\boldsymbol{z} & = \boldsymbol{\mu} + \boldsymbol{\Sigma}^{1/2}*\boldsymbol{\epsilon}
\end{align}
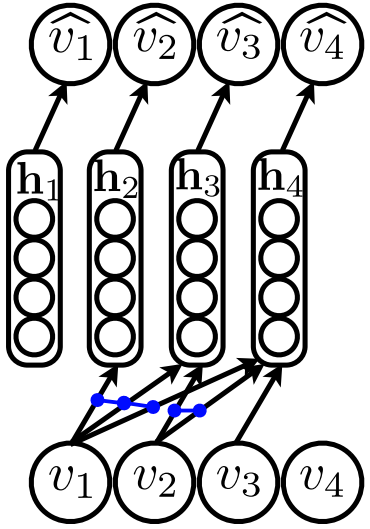
NADE
NADE(Neural Autoregressive Distribution Estimation)モデルは自己回帰モデルにニューラルネットを適応したモデルです.
NADEではデータ$\boldsymbol{x}\in \{0, 1\}^D$の各次元にあるオーダー$o$を与え,以下のような独立性を仮定をします:
p(\mathbf{x}) = \prod_{d=1}^D p(x_{o_d}|\mathbf{x}_{o_{<d}})
$p(x_{o_d}|\boldsymbol{x}_{o{<d}})$にはfeed-forwardニューラルネットを用います.
\begin{align}
p(x_{o_d} = 1|\boldsymbol{x}_{o_{<d}})
& =
\sigma(\boldsymbol{V}_{o_d,:}\boldsymbol{h}_d + b_{o_d}) \\
\boldsymbol{h}_{d}
& =
\sigma(\boldsymbol{W}_{:, o_{<d}}\boldsymbol{x}_{o_{<d}} + \boldsymbol{c})
\end{align}
NADEの特徴は各隠れ層$\boldsymbol{h}_d$への重み$\boldsymbol{W}$, $\boldsymbol{c}$を共有していることです.
これはRBMにおける平均場推論にインスパイアされていて,計算コストも抑えることができます.
学習では以下の負対数尤度を最小化します.
\mathcal{L} =
\frac{1}{N}\sum_{n=1}^N\sum_{d=1}^D-\ln p(x_{o_d}|\boldsymbol{x}_{o_{<d}})
また,オーダーに依らない生成を行うには負対数尤度に対し以下の期待値を計算します.
近似を行う場合はいくつかのランダムなオーダーでサンプリングし,その平均を計算します.
\mathbb{E}_{o \in D!}[-\ln p(\boldsymbol{x}|o)] \approx
\frac{1}{L}\sum_{l=1}^L -\ln p(\boldsymbol{x}|o^{(l)})
GAN
GANでは生成器$G(\boldsymbol{z})$と識別器$D(\boldsymbol{x})$の2つのネットワークを用います.
生成器$G(\boldsymbol{z})$は潜在変数$\boldsymbol{z}\sim p(\boldsymbol{z})$から学習データに似たデータを生成するネットワークであり,識別器$D(\boldsymbol{x})$は入力されたデータ$\boldsymbol{x}$が学習データなのか,生成器で生成されたデータなのかを判別するネットワークです.
GANの学習は以下のようなミニマックスゲームとして形式化されます.
\min_{G}\max_{D} \mathbb{E}_{\boldsymbol{x}\sim p_{data}}[\ln D(\boldsymbol{x})] +
\mathbb{E}_{\boldsymbol{z}\sim p(\boldsymbol{z})}[\ln(1-D(G(\boldsymbol{z}))) ]
識別器は与えられたデータが本物化偽物かを正しく識別しようと学習する一方で,生成器は識別器が分類を誤るように学習します.
この目的関数を生成器と識別器が交互に最適化することで学習を収束させます.
文書の表現学習
上で紹介したモデルを元に文書の表現を学習する手法をいくつか紹介します.
Replicated Softmax
Replicated SoftmaxはRBMを単語のカウントベクトルの生成に拡張したトピックモデルです.
文書を単語のカウントベクトル$\mathbf{v} \in \mathbb{N}^K$,文書中の単語数を$D$とするとエネルギー関数は
\begin{align}
E(\mathbf{v}, \mathbf{h}; \mathbf{\theta}) = -
\mathbf{h}^\mathrm{T}\mathbf{W}\mathbf{v} -
\mathbf{b}^\mathrm{T}\mathbf{v}- D \mathbf{a}^\mathrm{T}\mathbf{h}
\end{align}
となります.
可視変数,隠れ変数をそれぞれ固定したときの可視変数,隠れ変数の条件付き確率は次の式で表されます:
\begin{align}
p(h_j = 1 | \mathbf{v})
& =
\sigma(\mathbf{W}_{j,:}\mathbf{v} + Da_j) \\
p(v_{k} = 1 | \mathbf{h})
& =
\frac{\exp(\mathbf{W}_{:,w}^\mathrm{T}\mathbf{h} + b_w)}{\sum_{w'}\exp(\mathbf{W}_{:,w'}^\mathrm{T}\mathbf{h} + b_{w'})}
\end{align}
可視変数の確率はsoftmax関数によって表され,単語についての多項分布となります.
データを生成する際はこの分布から単語数回のサプリングを行うことでカウントベクトルを構成できます.
そして,この条件付き確率から各層についてサンプリングを行うことができるため,RBMと同様に学習を行うことができます.
文書検索による評価ではLDAに比べて高い精度を出しています.
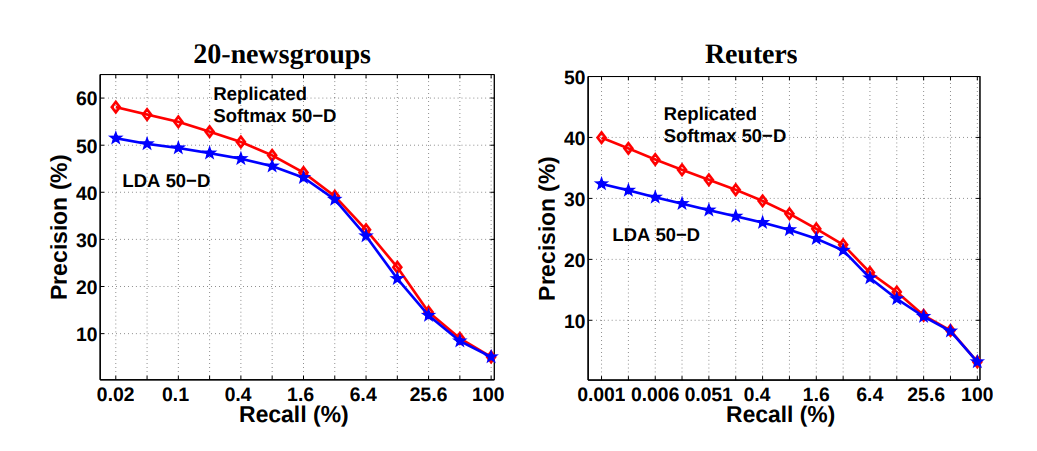
(引用: Replicated Softmax: an Undirected Topic Model)
DocNADE
NADEをRBMの平均場近似に基づいて設計したように,DocNADEはReplicated Softmaxの平均場近似から以下の様なfeed-fowardアーキテクチャを得ることができます.
ここで文書$\boldsymbol{x}$は単語のインデックスのシーケンスとして表されます.
\begin{align}
p(x_d=w|\boldsymbol{x}_{<d})
& = \frac{\exp(\boldsymbol{V}_{w,:}\boldsymbol{h}_d) + b_w}{\sum_{w'}\exp(\boldsymbol{V}_{w',:}\boldsymbol{h}_d) + b_{w'}} \\
\boldsymbol{h}_d
& = \sigma(\sum_{k<d}\boldsymbol{W}_{:,x_k} + \boldsymbol{c})
\end{align}
DocNADEではシーケンス中の単語毎に隠れ層が存在しますが,すべての単語の情報が埋め込まれた最後の層をその文書の表現として使います.
また,出力には通常のsoftmaxの代わりに階層的softmaxを用いることで計算量を削減することができます.
学習時には単語のオーダーによらないモデルを作るためにいくつかのオーダーで計算した尤度の平均を最大化します.
単語のオーダーを無視することで,DocNADEモデルはセマンティクスを維持しながら挿入可能な単語を予測することになります.
文書検索による評価ではRSMを上回る精度を出しています.
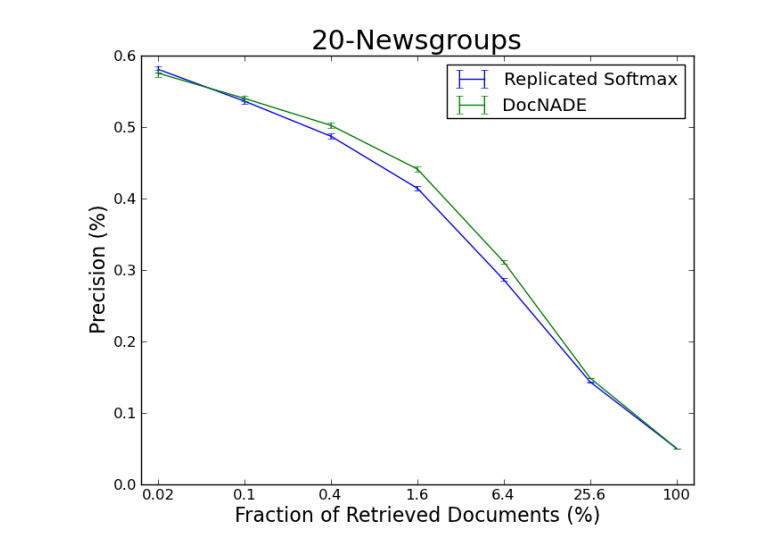
(引用: A Neural Autoregressive Topic Model)
Modeling documents with Generative Adversarial Networks
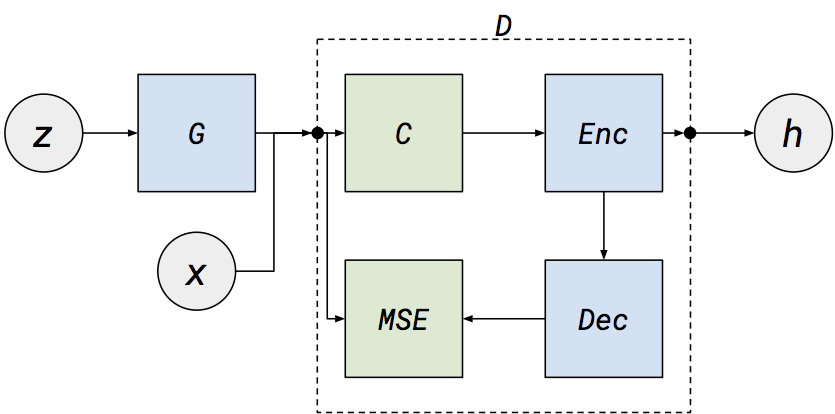
(引用:[Modeling documents with Generative Adversarial Networks](Modeling documents with Generative Adversarial Networks))
文書の表現学習にGANを使ったモデルです.
通常のGANとは異なり,識別器がDenoising Autoencoder(DAE)になっていて,その入出力のMSEをエネルギー関数とします.
識別器は与えられたデータが本物ならエネルギーを小さく,偽物なら大きくするように学習し,生成器はその逆の振る舞いを学習します.
具体的には以下のような最適化を行います.
\min_{D}\max_{G} \mathbb{E}_{\boldsymbol{x}\sim p_{data}}[D(\boldsymbol{x})] +
\mathbb{E}_{\boldsymbol{z}\sim p_{z}}[\max(0, m-D(G(\boldsymbol{z})))]
こうしたエネルギー関数を導入したGANはEnergy-Based GANと呼ばれます.
そして識別器であるDAEの中間層を文書の表現として用います.
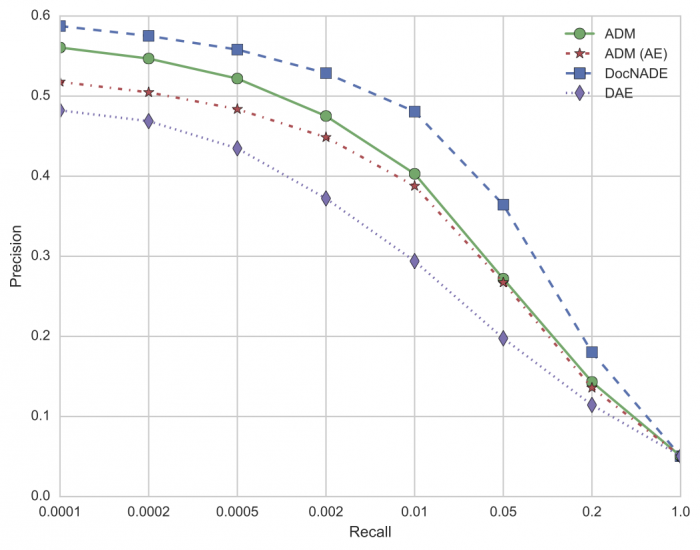
文書検索による性能評価は以下のように報告されています.
DAEより高い性能になってはいますが,そのほかの手法に比べれば劣っています.
実装
紹介したモデルを実装してみます.
Replicated Softmax
sklearn.neural_network.BernoulliRBMを参考にscikit-learn APIに準拠したRSMモデルを実装してみました.
疎行列にも対応しています.
勾配法によるパラメータの更新にはモーメンタムを導入しました.
scikit-learn API Implementation of Replicated Softmax (RSM)
RSM(n_components=128, learning_rate=0.001, batch_size=10, n_iter=10, k_cd_steps=1, momentum=0.9, verbose=False, random_state=None)
まとめ
ここまでニューラル生成モデルを使った文書の表現学習について紹介してきました.
どれも実装例が少なく,手軽に試せるライブラリもなかったりするので今後は各モデルについて汎用的な実装を作って実験してみようかと思います.