こちらの記事は,ロボティクスの辞書的な記事(にしたい記事)のコンテンツです.
- 事前に必要な知識(見ておいた方がいい記事)
お疲れ様です。秋並です。
今回は、ロボットアームの動作計画の中でも
- コンフュギュレーション空間を用いた動作計画
について解説します。
本記事内のコードはすべてgoogle colabratory上でも動作します(2024/8/31現在)。
本記事に出てくるコードはnotebook上で動作させる(「ipynb」ファイル)ことを前提としているため「py」ファイルでは一部のコードは動作しないのでご注意ください(主に描画関連)
コンフィギュレーション空間を用いた動作計画
お疲れ様です。秋並です。
今回は、「コンフィギュレーション空間を用いた動作計画」について解説していきたいと思います。
コンフィギュレーション空間とは
コンフィギュレーション空間とは、ロボットの構成(コンフィギュレーション)を表す空間のことです。
ここで「構成(コンフィギュレーション)」とは、位置や姿勢などの「ロボットがどのような状態であるか」を示します。
コンフィギュレーション空間上では、ロボットの取りうる構成が1つの点として表現されます。
一般的な表現だと少し分かりにくいので具体的な例を紹介します。
例えば、「根本が固定されている2自由度ロボットアーム」の場合、「2つの関節角度 $(\theta_1, \theta_2)$」が決まればそのロボットアームの構成(コンフィギュレーション)が確定するため、下図左のように $(\theta_1, \theta_2)$を軸とした2次元のコンフィギュレーション空間上で、1つの点として表現できます。
上記では、可視化しやすいように2次元のコンフィギュレーション空間の例を示しましたが、6自由度ロボットアームのような自由度が高いロボットの場合も、同様の考え方で6次元のコンフィギュレーション空間を定義することができます(4次元以上では可視化はできませんが)。
コンフィギュレーション空間を用いた動作計画
ここからは、コンフィギュレーション空間を用いた動作計画について解説していきます。なお、ロボットアームを対象とするため、以降は
- 「構成(コンフィギュレーション)」=「関節角度 $\vec{Q}$」
として扱います。
コンフュギュレーション空間を用いた動作計画の手順は以下のようになります。
- タスク空間において「初期手先位置$\vec{P}_{\mathrm{start}}$」と「目標手先位置$\vec{P}_{\mathrm{goal}}$」を決定します。
- タスク空間において逆運動学を用いて、「初期手先位置$\vec{P}_{\mathrm{start}}$」と「目標手先位置$\vec{P}_{\mathrm{goal}}$」に対応する「初期関節角度$\vec{Q}_{\mathrm{start}}$」と「目標関節角度$\vec{Q}_{\mathrm{goal}}$」を求めます。
- コンフィギュレーション空間において「初期関節角度$\vec{Q}_{\mathrm{start}}$」と「目標関節角度$\vec{Q}_{\mathrm{goal}}$」を結ぶ障害物と衝突しないような「関節軌道$\mathrm{Q}={\vec{Q}_1, \vec{Q}_2, \vec{Q}_3,\cdots, \vec{Q}_{n-1}, \vec{Q}_n }$」を求めます。
- 求めた「関節軌道$\mathrm{Q}$」を元に、ロボットの各関節を動かします。
コンフュギュレーション空間における動作計画(理想)
上記の手順をもう少し具体的に説明します。
最初に、コンフィギュレーション空間上における障害物について紹介します。
タスク空間において障害物と衝突するような関節角度をとった場合、コンフィギュレーション空間上でも障害物として写像されます。これを「コンフィギュレーション障害物」と呼びます。
コンフィギュレーション空間上で軌道を生成する場合も、もちろん障害物との衝突を避けるように軌道を生成する必要があるので、
理想的には以下手順のように
- 「コンフュギュレーション空間への衝突情報の写像」を行った後に
- コンフュギュレーション空間上で障害物を避けるような軌道を生成する
ことが理想的です。
1. 各関節角度を少しずつ変化させながら、衝突判定の結果に応じてタスク空間からコンフィギュレーション空間に障害物を写像することで、コンフュギュレーション空間に衝突情報を反映します。

2.「衝突情報が写像されたコンフィギュレーション空間」上で、「初期関節角度$\vec{Q}_{\mathrm{start}}$」と「目標関節角度$\vec{Q}_{\mathrm{goal}}$」を結ぶ軌道を生成します。(軌道の導出にはRRT等の経路計画法を使用)

3.生成した軌道に沿って各関節を動作させると、タスク空間でも障害物を避けるようにロボットアームが動作します。

上記は、2次元のコンフィギュレーション空間の例のため、全ての衝突情報をコンフュギュレーション空間に写像することが比較的容易です。
しかし、6自由度ロボットアームのような高次元のコンフィギュレーション空間の場合、現実的な計算時間で全ての衝突情報を写像することは不可能なので、このアプローチは難しいです。
例えば、各関節角度の稼働範囲が-180°~180°、関節の分解能が1度の$n$自由度ロボットアームの場合、$360^n$回の計算が必要になります。
仮に、1回の衝突判定に数ミリ秒かかるとしても、$n$ が高次元になると計算時間が膨大になります(次元の呪い)。
必要最低限の衝突判定で、コンフィギュレーション空間における動作計画を行う方法
このように、コンフィギュレーション空間を用いた動作計画では、衝突情報の写像、すなわち「衝突判定」の回数が処理時間に直結します。(動作計画の処理時間の90%が衝突判定ともいわれます)
そのため、実際の動作計画では、必要最低限の衝突判定で軌道を生成することが一般的です。
このような手法には、いくつかの種類がありますが、その中でも代表的な手法として「ランダムサンプリング法」や「軌跡最適化法」が挙げられます。
以降で、各手法について簡単に説明します。
(ただし、大まかな手順であり、実際の手法とは厳密には異なる箇所もあるため、そのまま実装しても適切に動作しないことに注意してください)
ランダムサンプリング法
ランダムサンプリング法では、以下のような手順で軌道を生成します。
- ランダムに「関節角度$\vec{Q}_{\mathrm{new}}$」をサンプリングします。
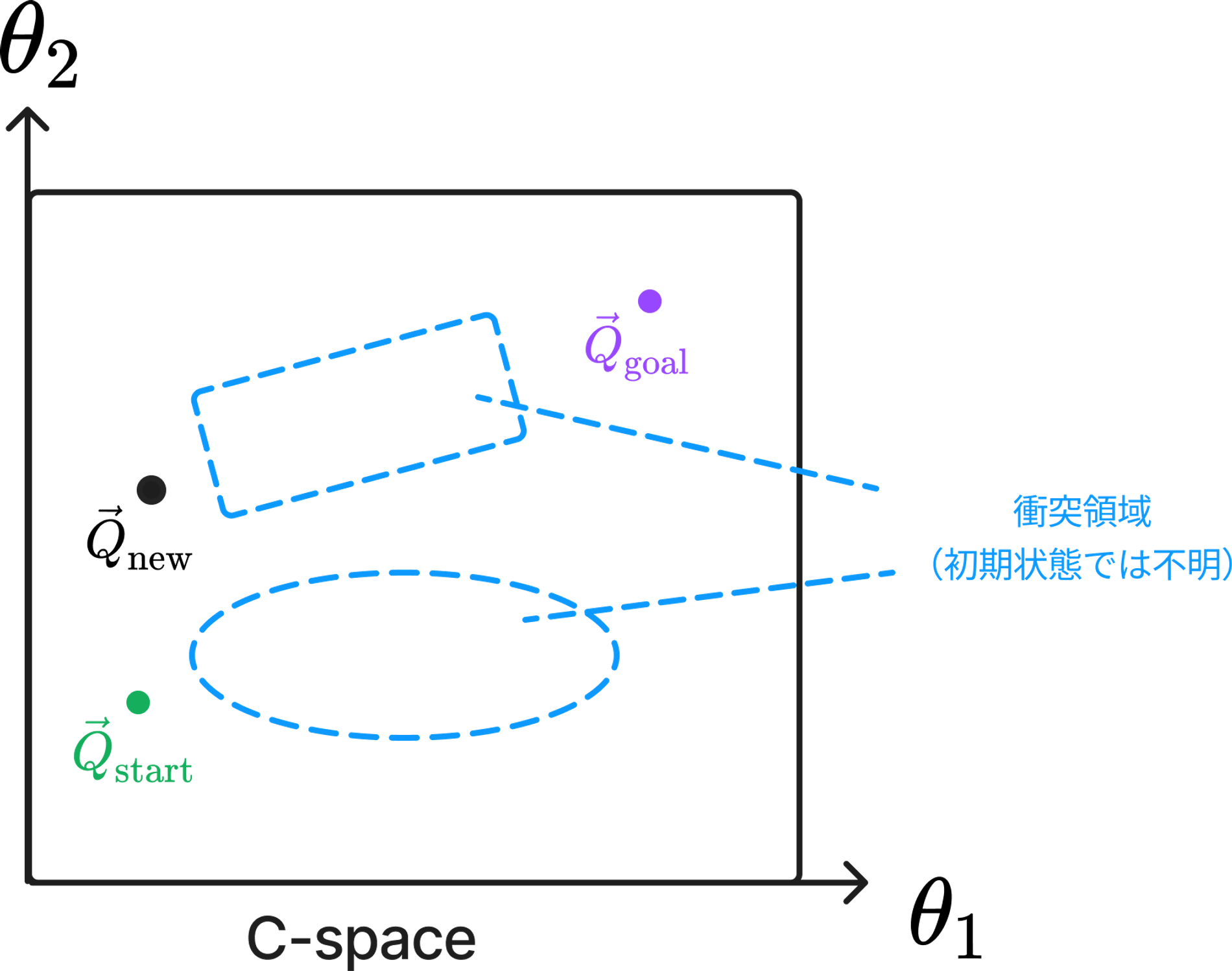
2.サンプリングした「関節角度$\vec{Q}_{\mathrm{new}}$」が障害物と衝突していないかを判定します。

3.障害物と衝突していない「目標関節角度$\vec{Q}_{\mathrm{new}}$」をノードとして採用します。

5.軌道上に障害物がないかを判定し、障害物がない場合は結んだ軌道を採用します。

6.軌道が「目標関節角度$\vec{Q}_{\mathrm{goal}}$」に到達するまで1~5を繰り返します。

上記の方法では、ランダムにサンプリングしたノード、及びノード間の軌道でのみ衝突判定を行えばよいため、計算時間を削減することが可能です。
軌跡最適化法
最適化法では、以下のような手順で軌道を生成します。
1.「初期関節角度$\vec{Q}{\mathrm{start}}$」と「目標関節角度$\vec{Q}{\mathrm{goal}}$」を結ぶ軌道を生成します。

2.軌道を一定の幅で分割し、各ノード間のコストを計算します。

3.コストが最小となるようにノードを動かします。(例えば、障害物と衝突している場合は、コストが大きくなるようにコストを設定する)

上記の方法でも、最適化するノード、及びノード間の軌道でのみ衝突判定を行えばよいため、計算時間を削減することが可能です。
コンフィギュレーション空間を用いた動作計画のメリットとデメリット
コンフィギュレーション空間を用いた動作計画には、以下のようなメリットとデメリットが存在します。
- メリット
- コンフィギュレーション空間上で軌道を求めるため、逆運動学を解くのは「初期関節角度$\vec{Q}_{\mathrm{start}}$」と「目標関節角度$\vec{Q}_{\mathrm{goal}}$」の2回だけで済む。
- デメリット
- コンフィギュレーション空間上で軌道を求めるため、実際に関節を動かした際に手先がどのように動作するかを予測するのが困難。
コード
上記の手順をpythonコードで実装した例が以下のようになります。
コードを実行すると下図のような
- コンフュギュレーション空間における軌跡
- タスク空間における軌跡
が描画されます
import math
import matplotlib.pyplot as plt
import numpy as np
def inverse_kinematics_2link(l1, l2, xe, ye):
"""
2次元平面上の2リンクロボットアームの逆運動学を求める
Parameters
----------
l1 : float
リンク1の長さ
l2 : float
リンク2の長さ
xe : float
手先のx座標
ye : float
手先のy座標
Returns
-------
theta1 : float
リンク1の関節角度(rad)
theta2 : float
リンク2の関節角度(rad)
"""
try:
# 代数的に求めた逆運動学の式
theta1 = -math.acos((xe**2 + ye**2 + l1**2 - l2**2)/(2 * l1 * math.sqrt(xe**2 + ye**2))) + math.atan2(ye, xe)
theta2 = math.acos((xe**2 + ye**2 - l1**2 - l2**2)/(2 * l1 * l2))
# 幾何学的に求めた逆運動学の式(「幾何学的」な手法を試したい場合は、下記のコメントを外してください)
# theta1 = math.atan2(ye,xe) - math.acos((-l2**2 + l1**2 + xe**2 + ye**2)/(2 * l1 * math.sqrt(xe**2 + ye**2)))
# theta2 = math.pi - math.acos((-xe**2 - ye**2 + l2**2 + l1**2)/(2 * l2* l1))
except: # 解が存在しない(xe, ye)を入力した場合、Noneを出力
theta1 = None
theta2 = None
return theta1, theta2
# 描画には各リンクの先端の座標が必要なので、求めたtheta1, theta2を使って順運動学を解く(描画しないなら不要)
# 同次変換行列(順運動学)← 「同次変換行列による順運動学」の記事はこちら https://qiita.com/akinami/items/9e65389929cedb1c9551
def make_homogeneous_transformation_matrix(link_length, theta):
"""
2次元平面における同次変換行列を求める
Parameters
----------
link_length : float
リンクの長さ
theta : float
回転角度(rad)
Returns
-------
T : numpy.ndarray
同次変換行列
"""
return np.array([[np.cos(theta), -np.sin(theta), link_length*np.cos(theta)],
[np.sin(theta), np.cos(theta), link_length*np.sin(theta)],
[ 0, 0, 1]])
##### ここを変更すると結果が変わります #######
# 各リンクの長さ
l1 = 2
l2 = 2
# 初期手先位置(実現可能な手先位置でないと解が求まりません)
x_start = 1.0
y_start = 3.0
P_start = np.array([[x_start],
[y_start]])
# 目標手先位置(実現可能な手先位置でないと解が求まりません)
x_goal = -2.0
y_goal = 2.0
P_goal = np.array([[x_goal],
[y_goal]])
resolution_deg = 3 # 関節軌道の分解能(手先軌道の分解のではないことに注意)
resolution_rad = math.radians(resolution_deg) # degree -> radian
############################################
# 軌道を描けるかを判定するための変数
enable_path = True
# 逆運動学によって「初期関節角度Q_start」を求める ####################################
theta1_start, theta2_start = inverse_kinematics_2link(l1, l2, P_start[0][0],P_start[1][0])
# 実現不可能な手先位置でないか確認
if theta1_start == None:
enable_path = False
Q_start = np.array([[theta1_start],
[theta2_start]])
##################################################################################
# 逆運動学によって目標関節角度Q_goalを求める ####################################
theta1_goal, theta2_goal = inverse_kinematics_2link(l1, l2, P_goal[0][0],P_goal[1][0])
# 実現不可能な手先位置でないか確認
if theta1_goal == None:
enable_path = False
Q_goal = np.array([[theta1_goal],
[theta2_goal]])
##################################################################################
# 「関節軌道Q = [Q_start, Q_2, Q_3, ..., Q_goal-1, Q_goal]」 を求める #############
# 今回は障害物がないため、Q_startとQ_goalを結ぶ直線を関節軌道とする。障害物がある環境では動作計画法(経路計画法)などを用いて障害物と衝突しないような軌道を求める。
d = math.sqrt((Q_goal[0][0] - Q_start[0][0])**2 + (Q_goal[1][0] - Q_start[1][0])**2) # Q_start <-> Q_goal 間の距離
divid_num = int(d/resolution_rad) # 軌跡dをresolution_radの分解能で分割するための分割数
Q_delta = np.array([[(Q_goal[0][0] - Q_start[0][0])/divid_num],
[(Q_goal[1][0] - Q_start[1][0])/divid_num]]) # 距離resolution_radだけ移動するための、theta_1, theta_2方向の微小移動量
Q = [Q_start] # 手先軌道Q
Q_current = Q_start.copy()
# Q_start -> Q_goal方向に resolution_radの分解能 で手先位置を移動させていき、「手先軌道P」を作成
while (0.001 < abs(Q_goal[0][0] - Q_current[0][0])) and (0.001 < abs(Q_goal[1][0] - Q_current[1][0])):
Q_current += Q_delta
Q.append(Q_current.copy())
##################################################################################
# 以下描画用 #######################################################################
fig = plt.figure(figsize=(10, 5))
ax1 = fig.add_subplot(1,2,1)
ax2 = fig.add_subplot(1,2,2)
# 軌道が求められた場合、描画する
if enable_path:
# 描画用にlink2の原点座標をまとめるlistを用意
o2_list =[]
oe_list = []
for i in range(len(Q)):
x1, y1 = 0, 0
# 同次変換行列による順運動学でlink2の原点座標、アームの先端座標を求める(この操作は描画しないのならば不要)
H12 = make_homogeneous_transformation_matrix(l1, Q[i][0][0])
H2e = make_homogeneous_transformation_matrix(l2, Q[i][1][0])
o2 = H12@np.array([[x1],
[y1],
[1]])
oe = H12@H2e@np.array([[x1],
[y1],
[1]])
o2_list.append(o2)
oe_list.append(oe)
# theta1, theta2の範囲を設定
ax1.set_xlim(-180, 180)
ax1.set_ylim(-180, 180)
# x,y 方向の範囲をlink1, link2を伸ばしきった長さにする
ax2.set_xlim(-(l1+l2),(l1+l2))
ax2.set_ylim(-(l1+l2),(l1+l2))
# 縦横比を同じにする
ax1.set_aspect('equal')
ax2.set_aspect('equal')
# コンフィギュレーション空間上での軌道、タスク空間上での手先の軌道、アームの軌道を描画
for i in range(len(Q)):
# リンク2の原点座標を取得
x2 = o2_list[i][0][0]
y2 = o2_list[i][1][0]
# アームの先端座標を取得
xe = oe_list[i][0][0]
ye = oe_list[i][1][0]
# アームを描画
ax2.plot([x1, x2], [y1, y2], color="tomato", lw=1) # link1の描画
ax2.plot([x2, xe], [y2, ye], color="lightgreen", lw=1) # link2の描画
# タイトルを設定
ax1.set_title("Configuration Space")
ax2.set_title("Task Space")
# 軸ラベルを設定
ax1.set_xlabel("theta1[deg]")
ax1.set_ylabel("theta2[deg]")
ax2.set_xlabel("x")
ax2.set_ylabel("y")
if i != 0:
# 現在関節角度をdegreeで取得
theta1 = math.degrees(Q[i][0][0])
theta2 = math.degrees(Q[i][1][0])
# 1つ前の関節角度をdegreeで取得
theta1_pre = math.degrees(Q[i-1][0][0])
theta2_pre = math.degrees(Q[i-1][1][0])
ax1.plot([theta1_pre, theta1], [theta2_pre, theta2], color="blue", lw=1) # コンフィギュレーション空間上の軌道を描画
xe_pre = oe_list[i-1][0][0]
ye_pre = oe_list[i-1][1][0]
ax2.plot([xe_pre, xe], [ye_pre, ye], color="blue", lw=1) # 手先の軌道を描画
print(f"Q[{i}] = ({math.degrees(Q[i][0][0]):.2f}°, {math.degrees(Q[i][1][0]):.2f}°)")
plt.show()
else:
print("実現不可能な軌道です。")
(おまけ)アニメーション
以下コードを実行すると、アニメーションで初期姿勢→目標姿勢に推移する様子が可視化できます。
from matplotlib.animation import FuncAnimation
from IPython.display import HTML
import math
import matplotlib.pyplot as plt
import numpy as np
def inverse_kinematics_2link(l1, l2, xe, ye):
"""
2次元平面上の2リンクロボットアームの逆運動学を求める
Parameters
----------
l1 : float
リンク1の長さ
l2 : float
リンク2の長さ
xe : float
手先のx座標
ye : float
手先のy座標
Returns
-------
theta1 : float
リンク1の関節角度(rad)
theta2 : float
リンク2の関節角度(rad)
"""
try:
# 代数的に求めた逆運動学の式
theta1 = -math.acos((xe**2 + ye**2 + l1**2 - l2**2)/(2 * l1 * math.sqrt(xe**2 + ye**2))) + math.atan2(ye, xe)
theta2 = math.acos((xe**2 + ye**2 - l1**2 - l2**2)/(2 * l1 * l2))
# 幾何学的に求めた逆運動学の式(「幾何学的」な手法を試したい場合は、下記のコメントを外してください)
# theta1 = math.atan2(ye,xe) - math.acos((-l2**2 + l1**2 + xe**2 + ye**2)/(2 * l1 * math.sqrt(xe**2 + ye**2)))
# theta2 = math.pi - math.acos((-xe**2 - ye**2 + l2**2 + l1**2)/(2 * l2* l1))
except: # 解が存在しない(xe, ye)を入力した場合、Noneを出力
theta1 = None
theta2 = None
return theta1, theta2
# 描画には各リンクの先端の座標が必要なので、求めたtheta1, theta2を使って順運動学を解く(描画しないなら不要)
# 同次変換行列(順運動学)← 「同次変換行列による順運動学」の記事はこちら https://qiita.com/akinami/items/9e65389929cedb1c9551
def make_homogeneous_transformation_matrix(link_length, theta):
"""
2次元平面における同次変換行列を求める
Parameters
----------
link_length : float
リンクの長さ
theta : float
回転角度(rad)
Returns
-------
T : numpy.ndarray
同次変換行列
"""
return np.array([[np.cos(theta), -np.sin(theta), link_length*np.cos(theta)],
[np.sin(theta), np.cos(theta), link_length*np.sin(theta)],
[ 0, 0, 1]])
##### ここを変更すると結果が変わります #######
# 各リンクの長さ
l1 = 2
l2 = 2
# 初期手先位置(実現可能な手先位置でないと解が求まりません)
x_start = 1.0
y_start = 3.0
P_start = np.array([[x_start],
[y_start]])
# 目標手先位置(実現可能な手先位置でないと解が求まりません)
x_goal = -2.0
y_goal = 2.0
P_goal = np.array([[x_goal],
[y_goal]])
resolution_deg = 3 # 関節軌道の分解能(手先軌道の分解のではないことに注意)
resolution_rad = math.radians(resolution_deg) # degree -> radian
############################################
# 軌道を描けるかを判定するための変数
enable_path = True
# 逆運動学によって「初期関節角度Q_start」を求める ####################################
theta1_start, theta2_start = inverse_kinematics_2link(l1, l2, P_start[0][0],P_start[1][0])
# 実現不可能な手先位置でないか確認
if theta1_start == None:
enable_path = False
Q_start = np.array([[theta1_start],
[theta2_start]])
##################################################################################
# 逆運動学によって目標関節角度Q_goalを求める ####################################
theta1_goal, theta2_goal = inverse_kinematics_2link(l1, l2, P_goal[0][0],P_goal[1][0])
# 実現不可能な手先位置でないか確認
if theta1_goal == None:
enable_path = False
Q_goal = np.array([[theta1_goal],
[theta2_goal]])
##################################################################################
# 「関節軌道Q = [Q_start, Q_2, Q_3, ..., Q_goal-1, Q_goal]」 を求める #############
# 今回は障害物がないため、Q_startとQ_goalを結ぶ直線を関節軌道とする。障害物がある環境では動作計画法(経路計画法)などを用いて障害物と衝突しないような軌道を求める。
d = math.sqrt((Q_goal[0][0] - Q_start[0][0])**2 + (Q_goal[1][0] - Q_start[1][0])**2) # Q_start <-> Q_goal 間の距離
divid_num = int(d/resolution_rad) # resolution_radの分解能で分割するための分割数
Q_delta = np.array([[(Q_goal[0][0] - Q_start[0][0])/divid_num],
[(Q_goal[1][0] - Q_start[1][0])/divid_num]]) # 距離resolutionだけ移動するための、theta_1, theta_2方向の微小移動量
Q = [Q_start] # 手先軌道Q
Q_current = Q_start.copy()
# P_start -> P_goal方向に resolution_radの分解能 で手先位置を移動させていき、「手先軌道P」を作成
while (0.001 < abs(Q_goal[0][0] - Q_current[0][0])) and (0.001 < abs(Q_goal[1][0] - Q_current[1][0])):
Q_current += Q_delta
Q.append(Q_current.copy())
##################################################################################
# 以下描画用 #######################################################################
fig = plt.figure(figsize=(10, 5))
ax1 = fig.add_subplot(1,2,1)
ax2 = fig.add_subplot(1,2,2)
# 軌道が求められた場合、描画する
if enable_path:
# 描画用にlink2の原点座標、手先座標をまとめるlistを用意
o2_list =[]
oe_list = []
for i in range(len(Q)):
x1, y1 = 0, 0
# 同次変換行列による順運動学でlink2の原点座標、アームの先端座標を求める(この操作は描画しないのならば不要)
H12 = make_homogeneous_transformation_matrix(l1, Q[i][0][0])
H2e = make_homogeneous_transformation_matrix(l2, Q[i][1][0])
o2 = H12@np.array([[x1],
[y1],
[1]])
oe = H12@H2e@np.array([[x1],
[y1],
[1]])
o2_list.append(o2)
oe_list.append(oe)
# jupyter book内にアニメーションを表示
def update(i):
ax1.cla()
ax2.cla()
# theta1, theta2の範囲を設定
ax1.set_xlim(-180, 180)
ax1.set_ylim(-180, 180)
# x,y 方向の範囲をlink1, link2を伸ばしきった長さにする
ax2.set_xlim(-(l1+l2),(l1+l2))
ax2.set_ylim(-(l1+l2),(l1+l2))
# 縦横比を同じにする
ax1.set_aspect('equal')
ax2.set_aspect('equal')
# リンク2の原点座標を取得
x2 = o2_list[i][0][0]
y2 = o2_list[i][1][0]
# アームの先端座標を取得
xe = oe_list[i][0][0]
ye = oe_list[i][1][0]
# アームを描画
ax2.plot([x1, x2], [y1, y2], color="tomato", lw=1) # link1の描画
ax2.plot([x2, xe], [y2, ye], color="lightgreen", lw=1) # link2の描画
# タイトルを設定
ax1.set_title("Configuration Space")
ax2.set_title("Task Space")
# 軸ラベルを設定
ax1.set_xlabel("theta1[deg]")
ax1.set_ylabel("theta2[deg]")
ax2.set_xlabel("x")
ax2.set_ylabel("y")
if i != 0:
for j in range(1, i+1):
# 現在関節角度をdegreeで取得
theta1 = math.degrees(Q[j][0][0])
theta2 = math.degrees(Q[j][1][0])
# 1つ前の関節角度をdegreeで取得
theta1_pre = math.degrees(Q[j-1][0][0])
theta2_pre = math.degrees(Q[j-1][1][0])
# コンフィギュレーション空間上の軌道を描画
ax1.plot([theta1_pre, theta1], [theta2_pre, theta2], color="blue", lw=1)
# 1つ前の手先座標を取得
xe = oe_list[j][0][0]
ye = oe_list[j][1][0]
# 1つ前の手先座標を取得
xe_pre = oe_list[j-1][0][0]
ye_pre = oe_list[j-1][1][0]
# 手先の軌道を描画
ax2.plot([xe_pre, xe], [ye_pre, ye], color="blue", lw=1)
ani = FuncAnimation(fig, update, interval=50, frames=len(Q))
HTML(ani.to_jshtml()) # HTMLに
# ani.save('motion_plan_task_space.mp4', writer="ffmpeg") # mp4で保存.これを実行すると処理時間が増加します
# ani.save('motion_plan_configuration_space.gif', writer="imagemagick") # gifで保存.これを実行すると処理時間が増加します
さいごに
今回は
- コンフュギュレーション空間を用いた動作計画
について解説しました。
以上で今回の解説を終わります。ロボティクスに興味のある方のお役に少しでも立てたら幸いです。






