過去に集めたデータのみを用いて強化学習を行うオフライン強化学習に注目が集まっています.ではオフライン強化学習は,オンラインで環境と作用し学習する一般的な強化学習と比べてどのようなメリットや,技術的な違いがあるのでしょうか?
本記事では,オフライン強化学習の基礎から最新の話題を橋渡しすることを目指します.まずオフライン強化学習のモチベーションから導入し,次に技術的に見たオンラインとオフラインの場合の違いを説明します.そして,オフライン強化学習における代表的な手法のひとつであるConservative Q-Leaning(CQL) と,その派生モデルのCOMBO, S4RLについて簡単に紹介します.(本記事ではモデルフリーQ学習が中心です)
また,最終章では本記事執筆にあたり行ったサーベイに基づく分野の未解決課題と今後の展望を独自の視点でまとめています.これらはあくまで個人的な所感ではありますが,オフライン強化学習の面白さを最もお伝えできる本記事ならではの章だと思っています.ぜひ最後まで読んでいただけたら嬉しいです.
なお,本記事は一般的な強化学習自体が初めての方でも,流れを追っていけばある程度理解できるように書いたつもりです.逆に,一般的な強化学習をマスターしている方にとっては最初の方は少々退屈かもしれないため,適宜読みとばしていただけたらと思います.
目次
- オフライン強化学習とは
- 一般的な強化学習を振り返る
- なぜ単純な拡張ではだめなのか?
- Conservative Q-Learning(CQL)
- CQLの発展版(COMBO, S4RL)
- まとめ
- 未解決課題と今後の展望
オフライン強化学習とは
オフライン強化学習はその名の通り,過去に集めたデータのみを使ってオフラインで強化学習を行おう,というものです[1-1].これは,学習に実環境とのインタラクションを必要とする従来の強化学習に対し,直接環境に作用することへの安全面でのリスクや経済的なコストを伴う医療や自動運転,ロボティクス,推薦システムなどの実応用の場面で期待を集めています.
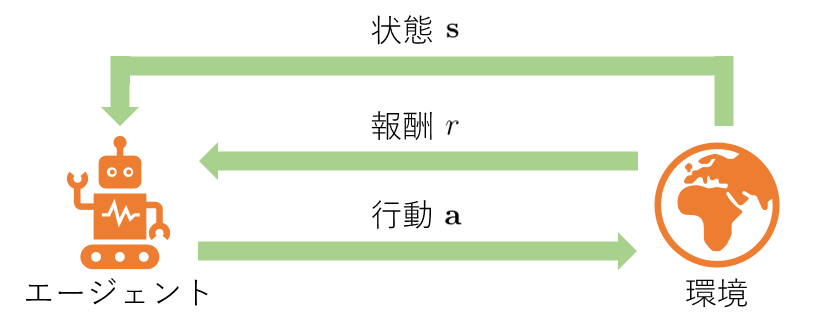
もう少し詳しくオフライン強化学習のモチベーションを説明します.まず,一般的な強化学習について簡単におさらいすると,これはエージェントと呼ばれる学習主体が環境とのインタラクションをしてフィードバックをもらいながら,ある目的関数の最適化を学習していく枠組みになっていました.この強化学習の学習フレームワークは非常に有用で,目的関数の設計次第で世の中の様々なシステムにおける制御や意思決定の最適化を担うことができます.2016年にAlphaGoと呼ばれるアルゴリズムが当時の囲碁の世界チャンピオンに勝利したというニュースはその一例です[2-1].このゲームAIと呼ばれる分野における強化学習の発展は目覚ましい一方で,実世界に目を向けてみると,Googleのデータセンターでの省電力化などいくつか取り組みはあるものの[2-2],実応用面での強化学習の活用はそれほど進んでいません.
では,なぜ強化学習を実応用することは難しいのでしょうか?その理由のひとつに,学習時の環境との相互作用におけるリスクやコストの存在が挙げられます.例えば,医療の場面で患者さんの容態の変化に対し,投薬などの治療介入を選択する場面を考えてみると,誤った治療判断には大きな危険があります.また広告配信などの場面でも,ユーザーに提示する広告により売上額に多額の差分が発生するため,経済的なコストがあります.特に,探索と活用のトレードオフの存在が知られている強化学習では,最適な意思決定を獲得できるまでに多くの非最適な選択による環境との作用を必要とします.この学習過程の実装は,リスクやコストへの懸念からなかなか容認できません.
そこで取りうるアプローチのひとつは,シミュレーション環境で強化学習アルゴリズムを学習することです.これは先に挙げた囲碁のゲームのように,環境を完全に再現できる場合は非常に有用です.この場合,シミュレータ上で膨大な回数の試行を繰り返すことで最適な(もしくは最適にかなり近い)エージェントの獲得が期待できます.しかし,実世界においては現実的なシミュレーションは多くの場合困難です.仮にシミュレーション上では性能が良さそうなエージェントを学習できたとしても,実環境で使ってみるとうまくいかないこともあります.このシミュレーションと現実のギャップをうまく乗り越えるためのsim2realという研究領域も非常に盛り上がっていますが[2-3],そもそもシミュレーションの実装自体もかなり時間や費用がかかってしまいます.そこで,実環境から集められたギャップの少ないデータを使って直接学習を行いたい,というモチベーションが生まれます.さらに,シミュレーションでうまくいったとしても実環境で性能が良いかどうかは分からないため,実際に実環境にデプロイする前に実環境から集めた過去のデータを使って性能推定できないか?というモチベーションもあります.
そこで期待を集めているのが,オフライン強化学習(Offline reinforcement learning) です.オフライン強化学習では(人手やルールベースも含む)過去に集めたデータのみを使って強化学習を行うため,大きく分けてふたつのやりたいことがあります.
1. 新たなエージェント(方策)の学習
過去に集められたデータのみを使って(実環境と作用することなく),オフラインで新たな(より良い)方策を学習する.
2. 方策の評価 / 最適方策の選択
複数の与えられた方策に対し,「仮にオンラインで動かした」ときの方策の性能を過去のデータのみを使ってオフラインで評価する.(オフ方策評価とも呼ばれる)
本記事では特に1. の新たなエージェント(方策)の学習に的を絞ってQ学習を中心に見ていきたいと思います.
※なお,オフライン強化学習はバッチ強化学習(Batch (constrained) reinforcement learning)とも呼ばれます.
一般的な強化学習を振り返る
オフライン強化学習について詳しく見ていく前に,まずは一般的な強化学習の定式化を振り返ります[1-2, 1-3].
基礎の基礎と定式化
強化学習では,まず環境からエージェントに対しある状態 $s \in \mathcal{S}$ が送られます.次に,エージェントはその状態に応じて方策 $\pi(a \mid s)$ に基づき,ある行動 $a \in \mathcal{A}$ を選択します.すると,環境はエージェントに対するフィードバックとして,状態と行動に依存して決まる報酬 $r \sim P_r(r \mid s, a)$ と次の状態 $s_{next} \sim \mathcal{T}(s_{next} \mid s, a)$ を返します.ここで,エージェントは再び次の行動 $a_{next} \sim \pi(a_{next} \mid s_{next})$ を選択して..という手順を繰り返していきます.この定式化において,$P_r(r \mid s, a)$ と $\mathcal{T}(s_{next} \mid s, a)$ はそれぞれ環境を特徴付ける報酬観測確率と状態遷移確率を表しています.
エージェントの目標は,将来的に得られる報酬を最大化するよう行動方策 $\pi$ を学習し,意思決定を最適化することです.目的関数となる将来得られる報酬の累積和は,一回の一連の試行(trajectory) $\tau$ 上で環境と作用する回数が $T+1$ 回のとき,割引率 $\gamma \in (0, 1]$ を用いて以下のように表すことができます.
$$J(\pi) = \mathbb{E}_{\tau \sim p_{\pi}(\tau)} \left[ \sum_{t=0}^T \gamma^{t} r(s_t, a_t) \right]$$
これは,方策 $\pi$ を取った場合に観測されるtrajectory上において得られる報酬の期待値を表しています.また,このtrajectoryの得られる確率は,報酬観測と状態遷移がエージェントのとる方策に依存するため,方策により取りうるtrajectoryが変わってくる,というのがポイントです.
$$\tau = { (s_t, a_t, s_{t+1}, r_{t}) }_{t=0}^T \sim d_0 (s_0) \prod_{t=0}^T \pi(a_t \mid s_t)\mathcal{T}(s_{t+1} \mid s_t, a_t)P_r(r_t \mid s_t, a_t)$$
なお, $d_0 (s_0)$ は一番最初の状態の観測確率です.
Q学習とActor-Critic
ここでは,Q学習とActor-Criticという手法に限定して一般的な強化学習の学習方法を振り返り,オフラインでの学習を考える準備をしていきます.(本章ではまだオフライン特有の話は登場しません)
Q学習
Q学習では,「価値」と呼ばれる概念を導入し,価値を最大化する行動方策 $\pi$ を取ることで,目的関数 $J(\pi)$ の最大化を目指します.ここで「価値」は,各期の即時報酬に加えて将来的な報酬への寄与を加味して定義されます.(例えば,不動産を購入すると一時的にはお金が減るため即時報酬としてはマイナスになりますが,長期的にみると家賃がかからない分将来報酬は増える,というイメージです.)これを数式で表すと,以下のように状態価値 $V^{\pi}(s_t)$ と行動価値 $Q^{\pi}(s_t, a_t)$ を定義できます.
$$V^{\pi}(s_t) = \mathbb{E}_{\tau_{t:T} \sim p_{\pi}(\tau_{t:T} \mid s_t)} \left[ \sum_{t^{\prime}=t}^T \gamma^{t^{\prime}-t} r_{t^{\prime}} \right]
\
Q^{\pi}(s_t, a_t) = \mathbb{E}_{\tau_{t:T} \sim p_{\pi}(\tau_{t:T} \mid s_t, a_t)} \left[ \sum_{t^{\prime}=t}^T \gamma^{t^{\prime}-t} r_{t^{\prime}} \right]$$
少々違いが分かりづらい式になってしまいましたが,状態価値 $V^{\pi}(s_t)$ はある状態 $s_t$ を訪れたとき,その後のtrajectory $\tau_{t:T}$ 上での期待報酬を表しています.一方,行動価値 $Q^{\pi}(s_t, a_t)$ はある状態を訪れたときに行動 $a_t$ を取った場合で条件づけた期待報酬になっています.一見して分かる通り,これらのふたつの価値の定義は非常に似ており,互いを関係づける次の関係式が存在します.
$$V^{\pi}(s_t) = \mathbb{E}_{a_t \sim \pi(a_t \mid s_t)} \left[ Q^{\pi}(s_t, a_t) \right]
\
Q^{\pi}(s_t, a_t) = r_t + \gamma \mathbb{E}_{s_{t+1} \sim \mathcal{T}(s_{t+1} \mid s_t, a_t)} \left[ V^{\pi} (s_{t+1}) \right]$$
つまり,状態価値は行動価値について方策上で期待値を取ったものになっており,行動価値は即時報酬に状態遷移後の状態価値を足し合わせたものになっています.この関係式を利用すると,上式の $V^{\pi}(s_t)$ を下式に代入することにより,(行動)価値の再帰的な関係式であるベルマン方程式が求められます.
$$Q^{\pi}(s_t, a_t) = r_t + \gamma \mathbb{E}_{s_{t+1} \sim \mathcal{T}(s_{t+1} \mid s_t, a_t), a_{t+1 \sim \pi(a_{t+1} \mid s_{t+1})}} \left[ Q^{\pi}(s_{t+1}, a_{t+1}) \right]$$
このベルマン方程式を使えば,原理的にはtrajectoryの後ろから順番に価値 $Q^{\pi}(s_t, a_t)$ を計算できます.その上で,各期毎に価値を最大化する行動を選択するargmax方策 $\pi(a_t \mid s_t) = \arg\max_{a_t} Q^{\pi}(s_t, a_t)$ を採用すれば,最適な方策を獲得できそうです.しかし,残念ながら現実にはそれは不可能です.なぜなら,真に最適な方策と価値を求めようとする場合,方策に依存する取りうる全てのtrajectoryについて期待報酬を求めないと最適な方策は特定できず,さらに方策に依存する価値も決めることができないからです.trajectoryの取りうる空間は大きすぎて厳密解を求めるのは現実的ではありません.そこで,Q学習では最適な方策における真の価値が分からないため,価値をパラメタ $\phi$ (例えば深層学習など)で関数近似し,近似価値関数 $Q^{\pi}_{\phi}$ によるargmax方策で方策の最適化を行います.
では,価値関数近似のためのパラメタ $\phi$ は一体どのように学習すれば良いのでしょうか?ここで活躍するのが先程出てきたベルマン方程式です.近似価値関数は,ベルマン方程式を用いて右辺と左辺の差分(temporal defference, TD誤差)からTD学習で学習できます.(右辺でmaxを取っているのはargmax方策によるためです)
$$Q^{\pi}_{\phi}(s_t, a_t) = r_t + \gamma \mathbb{E}_{s_{t+1} \sim \mathcal{T}(s_{t+1} \mid s_t, a_t)} \left[ \max_{a_{t+1}} Q^{\pi}_{\phi}(s_{t+1}, a_{t+1}) \right]$$
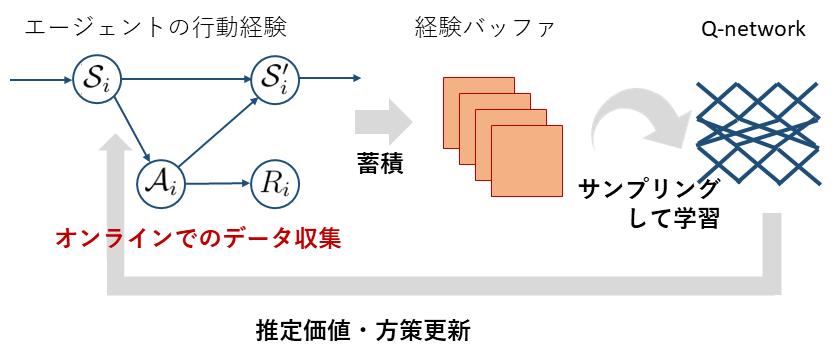
最後に,価値関数と方策は,方策により価値関数が変化し,価値関数により方策が変化するという相互の依存関係があるため,以下に示す手順で交互に更新し,方策を学習します.
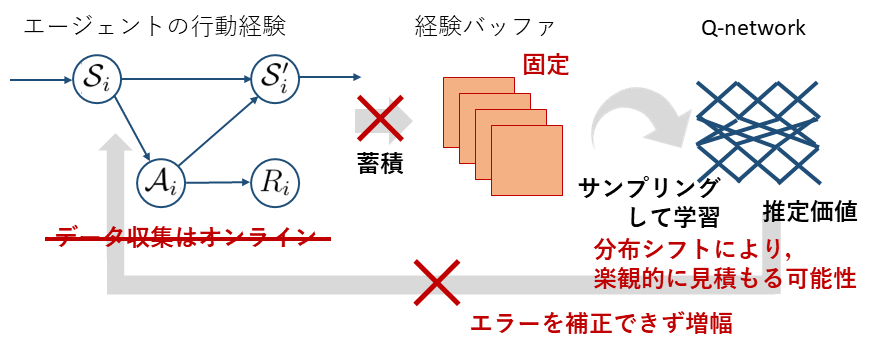
- 現在の方策に基づいて環境とインタラクションし,得られたフィードバックを含む行動記録 $(s_t, a_t, s_{t+1}, r_t)$ を経験バッファに追加・蓄積.
- 経験バッファから適当にデータをサンプリングしてきて,TD誤差により近似価値関数を学習・更新.
- 更新された近似価値関数を基に方策をアップデートし,再び1. に戻る.
なお,学習を安定化させるため,実際はTD学習する際に右辺を現在の近似価値で固定して,左辺側のパラメタのみに自由度を与えて近似価値関数のパラメタを更新することが多いです.さらに,貪欲的にargmaxの行動選択のみを行うと最終的な方策が局所最適になってしまうため,適当な微小な探索確率 $\epsilon$ を設定し,確率 $\epsilon$ でランダムな行動をエージェントに取らせて学習を促進します.(探索と活用のトレードオフと言われるものですね)
Actor-Critic
Actor-Criticについては,本記事ではそこまで踏み込んだ説明はしないつもりです.後で少し出てくるため簡単な紹介だけしておこうと思います.Actor-Criticは先程と同様,近似価値関数を用いてエージェントの方策更新を行うモデルですが,argmax方策をベースにしたQ学習とは方策の定義が少々異なります.具体的には,Actor-Criticでは価値関数だけでなく方策にもパラメタ $\psi$ (深層学習など) を導入して,方策の相対的な良さの勾配を基に方策をアップデートします.
$$\nabla_{\psi} J(\pi_{\psi}) = \mathbb{E}_{\tau \sim p_{\pi_{\psi}}(\tau)} \left[ \sum_{t=0}^T \gamma^t \nabla_{\psi} \log \pi_{\psi} (a_t \mid s_t) \widehat{A}(s_t, a_t) \right] $$
ここで,$\widehat{A}(s_t, a_t)$ はアドバンテージと呼ばれるもので,ある状態を訪れたとき,ある行動の相対的な良さを表しています.
$$\widehat{A}(s_t, a_t) = \widehat{Q}^{\pi_{\psi}}_{\phi}(s_t, a_t) - V^{\pi_{\psi}}_{\phi}(s_t)
\
V^{\pi_{\psi}}_{\phi}(s_t) = \mathbb{E}_{a \sim \pi_{\psi}(a \mid s_t)} \left[ \widehat{Q}^{\pi_{\psi}}_{\phi}(s_t, a) \right]$$
Actor-Criticの良いところは,先程のQ学習が主に離散行動空間を扱うものであるのに対し,勾配によるアップデートを用いていることで連続行動空間に対応できる点です.また,argmax方策に比べてより確率的に行動を選択する方策を扱いやすいというメリットもあります.中でもSoft Actor-Critic(SAC)という手法は期待報酬最大化を目指しつつ,同時になるべく方策の確率的な乱雑さ(エントロピー)を最大化することにより良い汎化性能が得られることが知られています[3-1, 3-2].
なお,これらのQ学習をベースにした手法は一般にオフポリシー強化学習と呼ばれますが,その名称の所以は次章の後半で説明します.
なぜ単純な拡張ではだめなのか?
さて,準備が整ったところで,オフライン強化学習の話に入っていきます.
データの特徴
まず始めに,オフライン強化学習に使えるデータの特徴を見てみます.このデータは,過去のある方策により集められた $n$ 回分の有限個のtrajectoryで構成されています.各trajectoryでは,環境と方策によりどのような状態遷移が行われ,フィードバックとしてどの程度の報酬が得られたかが記録されています.
$$\mathcal{D} = { \tau_1, \ldots, \tau_n }
\
\tau_i = {(s_t^i, a_t^i, s_{t+1}^i, r_t^i)}_{t=0}^T$$
ここで重要なのは,これらのデータは過去に集められた固定されたデータセットのものであるため,観測された状態遷移と報酬はデータ収集時の方策に依存している点です.言い換えると,選ばれた行動以外の場合の結果は記録されていません.そのため,過去の方策により選ばれなかった反実仮想な行動に対しては,フィードバックを推論する必要のあるデータになっています.
さらに,各trajectoryの観測確率はデータ収集方策に依存しているという性質上,使えるデータは必ずデータ収集方策 $\pi_{\beta}$ の影響を受けたバイアスのかかったデータになっています.
$$\tau_i \sim d_0(s_0) \prod_{t=0}^T \pi_{\beta}(a_t \mid s_t) \mathcal{T}(s_{t+1} \mid s_t, a_t) P_r(r_t \mid s_t, a_t)$$
このオフライン強化学習のふたつのデータ特性
- 選ばれた行動以外のフィードバックが得られない.
- データ分布がデータ収集時の方策に依存したバイアスのかかったものになっている.
こそが,これから解説するオフライン強化学習の技術課題に繋がっており,この技術的課題をどう克服していくのかを考えるのがオフライン強化学習の面白いところであると筆者は考えています.
※なお,以降では説明の都合上,データ収集時の方策 $\pi_{\beta}$ をbehavior policyと呼び,これから新たに学習したい方策のことを $\pi_{\theta}$ と書き,current policyと呼びます.
分布シフトの発生
というわけで,ここでは先に見たデータの特性により発生するオフライン強化学習の技術課題である,分布シフト(distribution shift) について説明しようと思います.
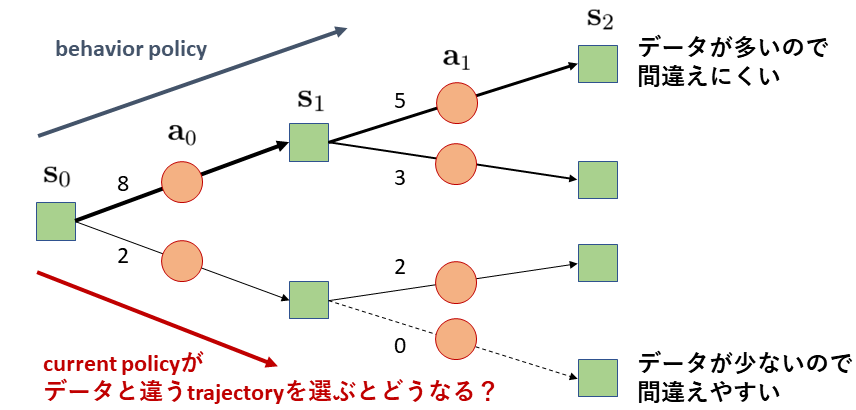
まずは具体例から見ていきましょう.先程集めてきたtrajectoryのデータが今10個あり,以下の図において矢印の傍の数字で示すようにデータ数が分岐している状況を考えてみます.
図を見ると,behavior policyは上の方のtrajectoryを多く選んでいるようです.ではここで,方策の分布シフトが起こっている,すなわち,current policyがbehavior policyにより集められたデータの少ない,下側のtrajectoryを取ろうとしている状況について考えてみたいと思います.
まず始めに $s_0$ の状態に対しbehavior policyは上の $a_0$ を主に選んでいたのに対し,current policyが下の $a_0$ を高い確率で選んでいた場合,エージェントの取った行動に応じて次の状態の観測されやすさが異なってきます.例えば,図ではbehavior policyによるデータ分布上では $s_1$ は上対下が8:2なのに対し,current policyでは上対下が4:6になるかもしれません.このように,方策の分布シフトにより引き起こされる,behavior policyの集めたデータ上とcurrent policyが取るはずのtrajectory上で状態遷移確率やデータ生成確率が異なることを,状態の分布シフトと呼びます.
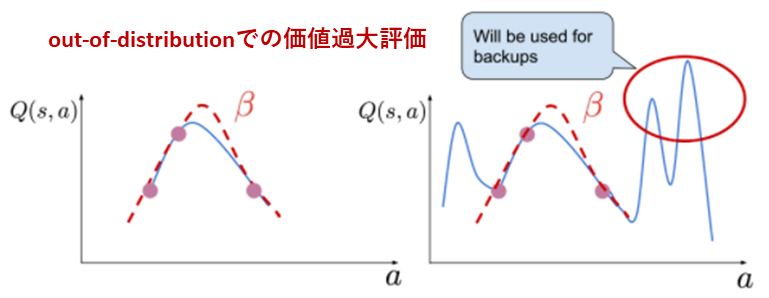
状態の分布シフトが起こるのはどのような状況かというと,これはcurrent policyが過去のデータの少ない未知の領域に入ってしまうことを意味しています.つまり,図で言う一番下のtrajectoryのような,behavior policyがカバーしておらずデータの集まっていない領域に入ってしまう可能性があります.すると,このデータのない領域はout-of-ditributionのため価値関数や期待報酬を予測する際に不確実性が高くエラーが大きい領域になります.ここで価値関数が誤って価値を過大評価してしまうと,current policyは価値を最大化する行動選択を行うため,更にbehavior policyと異なる方策を選んで方策の分布シフトが拡大して..と悪循環が起こってしまいます.
まとめると,オフラインでは以下のように分布シフトが発生する悪循環が起こってしまうことが分かります.
1. 方策の分布シフト
current policyがbehavior policyと異なる行動方策を選択.
2. 状態の分布シフト
current policyとbehavior policyではtrajectory上での状態生成確率が異なり,current policyがデータの少ない,out-of-distributionな領域に.
3. 価値関数の予測エラー
データが少ない領域では予測不確実性が大きく,エラーが発生.
4. 価値の過大評価により再び1. に戻る
誤った価値の過大評価が起こると,価値最大化により方策の分布シフトが拡大.
また,テクニカルな部分を見てみても,Q学習は分布シフトとデータ特性の影響により,ふたつの学習がうまくいかない学習の特徴があります.
- そもそもTD学習のロスを計算してパラメタをアップデートするために,選ぶデータサンプルの生成確率がbehavior policyの集めたデータ上とcurrent policy上で異なる.
- TD学習でtargetとして誤差を取る右辺の部分で,データ上で記録された行動だけでなくout-of-distributionな $(s_{t+1}, a_{t+1}^{\prime})$ に対しても価値を算出する必要があるが,ここで過大評価が起こるとエラーが逆伝播してしまう.
$$\widehat{Q}^{\pi}_{\phi}(s_t, a_t) \leftarrow r_t + \gamma \mathbb{E}_{s_{t+1} \sim \mathcal{T}(s_{t+1} \mid s_t, a_t)} \left[ \max_{a_{t+1}^{\prime}} Q^{\pi}_{\phi_{target}}(s_{t+1}, a_{t+1}^{\prime}) \right]$$
特に2. のエラーが伝播してしまう問題は深刻で,一般的なQ学習ベースの強化学習モデルを単純にオフラインに適用するのは困難になってしまいます.
※なお,上式で使用しているように,実際にはデータ上には記録されていないかもしれない反実仮想な行動や状態の定式化は,以降ではプライムをつけて区別していきたいと思います.(例えば $a_{t+1}^{\prime}$ など)
unlearning effect
上記の学習がうまくいかないことが原因で,オフライン強化学習では特有のunlearning effectの存在が知られています.
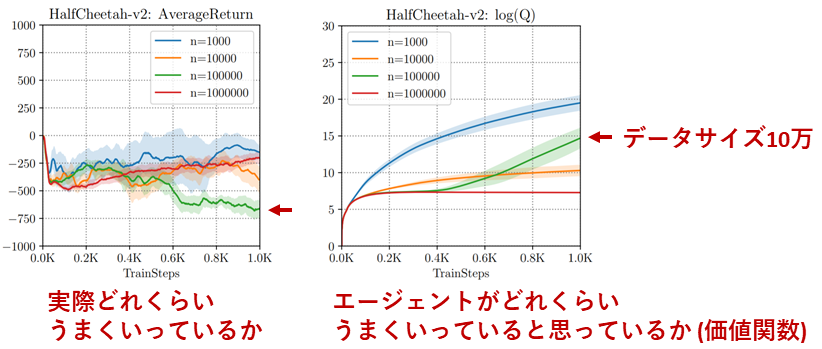
以下の図は,A. Kumar et al.により報告された,SACという一般的な強化学習アルゴリズムを'HalfCheetah-v2'というタスクでオフライン強化学習に単純に適用してみた結果です[4-2].左の図は,オフラインで学習したエージェントをオンラインで動かしてみたときに得られた平均報酬,すなわち実際にエージェントがどれくらいの性能を獲得しているのかを表しています.一方,右の図は価値関数の出力を見ることで,エージェントがどのくらいうまくいっていると思っているかを表しています.
まず左の図を見ると,青→オレンジ→緑→赤とデータサイズを増やし学習ステップ数を増やしても,全く汎化していないことが分かります.(一般的な教師あり機械学習では基本的にデータサイズや学習ステップを増やせば性能は上がっていくことが期待されますが,オフライン強化学習ではそうはいかないようです)
特に緑のデータサイズ10万の時に注目してみると,そもそも性能が非常に悪いだけでなく学習すればするほど性能が悪化してしまっているのが分かります.ではその時エージェントがどれくらいうまくいっていると思っているか?を右図の価値関数をもとに見てみましょう.すると,このエージェントは学習を重ねるごとにどんどんその価値関数が上昇しています.つまり,緑のエージェントは自分では学習がうまくいっていると思っている一方で,実際には全然うまく学習できていない,という状況が起こっています.
実はこの原因となっているのが,先に述べたout-of-distributionな行動に対する価値関数の過大評価の伝播とその増幅です.まず,価値関数が過大評価されているため,エージェントはうまく行動選択を行えていると思っています.一方,実際には予測エラーで価値が高くなっているだけで期待報酬が高いわけではないため,価値を最大化する方策を取っても期待報酬を最大化できず,学習が壊滅的になってしまっています.これは一般的な機械学習や深層学習の文脈で語られる過剰適合(overfitting)とは少々事情が異なるため,unlearning effectと呼ばれています.
※少し補足すると,unlearning effectにより,オフライン強化学習では学習を重ねるごとに性能が悪化してしまう場合があります.そのため,何エピソード学習した段階の結果を抜き取るかにより学習したアルゴリズムの性能評価やアルゴリズム間の性能順位が大きく異なる場合があります.これを踏まえ,(一般的な強化学習でもそうかもしれないですが)オフライン強化学習では特に,学習後の期待報酬を性能として見るよりは,上図のような学習曲線を基にアルゴリズムの安定的な性能を判断する必要があると言えます.
補足:逆になぜオフポリシーではうまくいったのか?
ここまでの議論を見ていると,前章で扱ったオフポリシーの強化学習であっても,経験バッファに蓄積したデータを使って近似価値関数を学習する以上,オフラインの場合と似た問題は起こるのではないか?という疑問が湧いてくるかもしれません.それはとても鋭い指摘で,実はオフポリシーの場合でも,分布シフトの問題は発生しています.ではなぜオフポリシーの場合ではうまく学習できていたのか,ここではオフラインとの違いも含めて明らかにしていきます.
まず始めに,オフポリシーの場合でも分布シフトが起こっていた,というのはどういうことなのでしょうか?オフポリシーの強化学習の方法を思い出してみると,これは経験バッファから適当にサンプリングしてきたデータを使ってTD学習する,というものでした.このときバッファの最大データサイズは固定されており,バッファには現在のpolicyにアップデートされる前の少し古いpolicyを使って集められたデータが蓄積されています...ということは,経験バッファ上にあるデータは現在のpolicyにより集められたデータではなく,方策の分布シフトが多かれ少なかれ起こってしまうはずですよね?これがオフポリシー強化学習がオフポリシーと呼ばれる所以で,一般的な(オフライン強化学習ではない)設定でのオフポリシー強化学習でも方策の分布シフトは確かに起こってしまいます.
そのため,Q学習がオフライン強化学習でうまく学習できない条件であった以下のふたつの点は,実は(オフラインではない一般的な場面の)オフポリシー強化学習にも残念ながら当てはまります.
- そもそもTD学習のロスを計算してパラメタをアップデートするために,選ぶデータサンプルの生成確率が,更新される前の少し古いpolicyの集めたデータ上と現在のpolicy上で異なる.
- TD学習でtargetとして誤差を取る右辺の部分で,データ上で記録された行動だけでなくout-of-distributionな $(s_{t+1}, a_{t+1}^{\prime})$ に対しても価値を算出する必要があるが,ここで過大評価が起こるとエラーが逆伝播してしまう.
$$\widehat{Q}^{\pi}_{\phi}(s_t, a_t) \leftarrow r_t + \gamma \mathbb{E}_{s_{t+1} \sim \mathcal{T}(s_{t+1} \mid s_t, a_t)} \left[ \max_{a_{t+1}^{\prime}} Q^{\pi}_{\phi_{target}}(s_{t+1}, a_{t+1}^{\prime}) \right]$$
実際に,(オフラインではない一般的な場合の)強化学習でも以下に示すdeadly triadの3条件が同時に揃ってしまうと一般に学習が困難になることが知られています[1-2, 4-3].つまり,オフポリシー強化学習はこの3条件を満たしてしまうため学習が困難ということです.
- TD学習
- 価値の関数近似
- オフポリシー(方策の分布シフトが発生)
では,どうしてオフポリシー強化学習が(オフラインではない)一般的な設定で実際に(経験的に)はうまく学習が行えることが多いのかというと,それはアップデートした方策により環境と新たにインタラクションしフィードバックを集められるからです.これにより,経験バッファ内の一部古いデータを新しいデータに置き換えていくことで方策の分布シフトの程度をある程度小さく保てるというのが学習を安定化させるひとつ目の理由になっています.また,仮にout-of-distributionな $(s_{t+1}, a_{t+1}^{\prime})$ ペアへの価値の過大評価が起こりそれに基づいてpolicyがアップデートされたとしても,新たにバッファに追加された環境からのフィードバックデータがいずれはサンプリングされ,TD学習により過大評価が補正されます.これにより,一般的なオフポリシー強化学習では次第に最適に近い方策とその方策もとでの収束した価値関数を獲得できることになります.
逆の言い方をすれば,オフライン強化学習では追加的なデータが得られないという点において,一度エラーが起こると修正が効かないどころかエラーがどんどん増幅してしまうため,学習が非常に困難になっていると言えるでしょう.
Conservative Q-Learning
さて,Conservative Q-Learningまでの道のりが少々長くなってしまいましたが,ここからが本番です.いよいよ(本記事執筆時点における)オフライン強化学習の代表的な手法のひとつであるConservative Q-Learning(CQL)[5-1]がどのように前述の課題(unlearning effect)を解決しようとしているのか,紹介していきます.
背景
前章で述べたように,オフライン強化学習では実環境からのフィードバックから得られない状況でout-of-distributionな行動に対し価値の過大評価が起こってしまい,それがTD誤差による価値関数の学習により増幅されてしまうことが,学習が失敗する主な原因になっていました.この問題に対し,CQL以前に取られていたアプローチは大きく分けて2つあります.
- behavior policyとcurrent policyが離れすぎないように方策間の分布シフトの程度に直接制約をかける.
- 価値関数の不確実性を用いて価値の推定下界を最大化する方策を獲得する.
それぞれどういうことか簡単に説明します.まず,1. の背景には,behavior policyにより集められたデータがカバーしていない領域において価値関数の予測エラーがより大きくなってしまう問題があります.そこで,behavior policyとある程度挙動が似ている範囲で新たな方策を学習することで,近似価値関数の学習を安定化させようというのが1. の意図です.これは直観的にはbehavior policyの選んだtrajectoryの近傍からより良い方策やtrajectoryを獲得しようとしている,と言い換えられます.また,分布シフトへの制約の具体的な例には,behavior policyとcurrent policyの間でKLダイバージェンスを報酬に対する罰則項として使用する方法などがあります[5-2, 5-3].
一方,仮に1. のように方策の乖離制約を書けたとしても,ベルマン方程式の右辺のmaxの部分が原因で価値関数の学習ではどうしてもエラーが起こってしまいます.そのため,2. のアプローチは,その不確実性を考慮した方策アップデートを行おう,というものです.具体的には,例えばブートストラップで価値関数を求める場合[5-4],価値の平均値だけでなく,価値のばらつきも求められます.すると,ある確率以上での価値の下界がどれくらいになりそうか見積もることができます.そこで,その価値の下界を最大化する方策を選択することで,不確実な環境下でも最低限の性能が保証される方策が獲得できるだろうという算段です.
しかし,上記のふたつの方法はよく考えてみると,オフライン強化学習において学習がうまくいかない原因の根本的解決にはなっておらず,対症療法的なアプローチになっていることが分かります.振り返ると,そもそもの学習上の問題は,TD誤差の右辺のmaxを取る部分でout-of-distributionな行動に対してQ値を予測する必要があり,過大評価が起こってしまうこと,そしてそのエラーがTD誤差学習により増幅してしまうことが原因でした.にも関わらず,方策制約も不確実性考慮もその問題に直接対処している訳ではありません.では,そもそも価値関数のエラーが起こりにくい,あるいは,エラーが起こったとしても,その伝播や増幅を抑制できる学習方法を考えることはできないのでしょうか? このエラーが発生しにくい学習方法を考えたい,というモチベーションからA. Kumar et al.により提案されたのが,これから紹介するCQLです.
CQLでやっていること
CQLでは価値関数の学習において,得られたデータ点に対しては価値をなるべく正確に近似する一方で,out-of-distributionで不確実性の高い状態と行動のペアに対しては保守的(conservative)に価値を見積もることで価値の過大評価を抑制しよう,というアプローチになっています.この発想を基に,CQLの価値学習の更新式は以下のように定義されます.
$$
\begin{aligned}
\widehat{Q}^{\pi_{\theta}}_{\phi} & \leftarrow
\arg \min_{Q_{\phi}} \mathbb{E}_{(s_t, a_t, s_{t+1}, r_t) \sim \mathcal{D}} \left[ \alpha \left( \max_{\pi^{\prime}} \mathbb{E}_{a_t^{\prime} \sim \pi^{\prime}(a_t^{\prime} \mid s_t)} \left[ Q_{\phi} (s_t, a_t^{\prime}) \right] - Q_{\phi} (s_t, a_t) \right) \right. \
&\quad \quad \quad + \frac{1}{2} \left( Q_{\phi}(s_t, a_t) - \left( r_t + \gamma \mathbb{E}_{a_{t+1}^{\prime} \sim \pi_{\theta}(a_{t+1}^{\prime} \mid s_{t+1})} \left[ Q_{\phi_{target}}^{\pi_{\theta}} (s_{t+1}, a_{t+1}^{\prime}) \right] \right) \right)^2 \biggr]
\end{aligned}
$$
ここで $\alpha$ は適当なハイパーパラメタです.この式は以下のように大きく3つの項に分けることができます.
- $\arg\min_{Q_{\phi}} \mathbb{E}_{\mathcal{D}} \left[ \max_{\pi^{\prime}} \mathbb{E}_{a_t^a{\prime} \sim \pi^{\prime}(a_t^{\prime} \mid s_t)} \left[ Q_{\phi} (s_t, a_t^{\prime}) \right] \right]$
- $\arg\min_{Q_{\phi}} \mathbb{E}_{\mathcal{D}} \left[ Q_{\phi} (s_t, a_t) \right]$
- $\arg\min_{Q_{\phi}} \mathbb{E}_{\mathcal{D}} [ ( Q_{\phi} (s_t, a_t) - ( r_t + \gamma \mathbb{E}_{a_{t+1}^{\prime} \sim \pi_{\theta}(a_{t+1}^{\prime} \mid s_{t+1})} [ Q_{\phi_{target}}^{\pi_{\theta}} (s_{t+1}, a_{t+1}^{\prime}) ] ) )^2]$
おそらく一番直観的なのは3. の項かと思います.これは,これまで通りTD誤差を最小化する項になっています.では,後の2つの項は一体なにをやっているのでしょうか?ひとつ目の項は,まず $\max_{\pi^{\prime}}$ の部分でデータ上の $s_t$ に対し価値が最大となる(データ上にない $a_t^{\prime}$ を選ぶかもしれない)方策を選択した後,$\arg\min_{Q_{\phi}}$ でなるべくその価値を小さくしようとしています.つまり,ある最悪ケースの方策上において価値の過大評価を抑制するための項になっていることが分かります.これなら価値の過大評価は抑制できそうです.その一方で,本来は価値が高いところを過小評価しすぎてしまうことはないのでしょうか?この価値関数が過度に悲観的になって価値の過小評価をしてしまうのを抑制するのが,実はふたつ目の項になっています.ふたつ目の項ではデータ上の $(s_t, a_t)$ ペアに対してはその価値を符号を反転させて$\arg \min_{Q_{\phi}}$していることから,データ上の $(s_t, a_t)$ ペアに対してはなるべく価値を大きく見積もる近似価値関数のパラメタを選択するようにしています.
このように,CQLではデータが得られている部分に対してはなるべく価値を大きく正当に評価し,一方でデータのない不確実性の高い部分に対しては価値を低く見積もることで,過大評価を抑制しつつも価値をうまく近似しようとしているのが分かります.また,CQLは価値の推定下界を最大化する方策を獲得できることが理論的に証明されています.(詳しくは論文参照)
CQLの発展版
最後に,CQLの拡張としてほぼ同時期に提案された,COMBOとS4RLというふたつの手法について簡単に紹介したいと思います.
COMBO
COMBOはCQLをモデルベース強化学習に拡張した手法となっています[6-1].モデルベース強化学習では,状態遷移確率 $\mathcal{T}(s_{next} \mid s, a)$ と報酬観測確率 $P_r(r \mid s, a)$ を明示的にモデル化して学習し,学習したモデル $\widehat{\mathcal{M}}$ 上で方策を動かすこと(rollout)で学習を行います.
このとき,COMBOにおける価値関数の更新式は以下のように定義されます.
$$
\begin{aligned}
\widehat{Q}^{\pi_{\theta}}_{\phi} & \leftarrow
\arg \min_{Q_{\phi}} \alpha \left( \mathbb{E}_{s^{\prime} \sim d_{\widehat{\mathcal{M}}}(s^{\prime}), a^{\prime} \sim \pi_{\theta}(a^{\prime} \mid s^{\prime})} \left[ Q_{\phi}(s^{\prime}, a^{\prime}) \right] - \mathbb{E}_{(s_t, a_t) \sim \mathcal{D}} \left[ Q_{\phi}(s_t, a_t) \right] \right) \
&+ \displaystyle \frac{1}{2} \beta \mathbb{E}_{(s_t, a_t, s_{t+1}, r_t) \sim \mathcal{D}} \left[ Q_{\phi}(s_t, a_t) - \left( r_t + \gamma \mathbb{E}_{a_{t+1}^{\prime} \sim \pi_{\theta}(a_{t+1}^{\prime} \mid s_{t+1})} \left[ \left( Q_{\phi_{target}}^{\pi_{\theta}} (s_{t+1}, a_{t+1}^{\prime}) \right] \right) \right)^2 \right] \
&+ \displaystyle \frac{1}{2} \left( 1 - \beta \right) \mathbb{E}_{(s^{\prime}, a^{\prime}, s_{next}^{\prime}, r^{\prime}) \sim \widehat{\mathcal{M}}} \left[ Q_{\phi}(s^{\prime}, a^{\prime}) - \left( r^{\prime} + \gamma \mathbb{E}_{a_{next}^{\prime} \sim \pi_{\theta}(a_{next}^{\prime} \mid s_{next}^{\prime})} \left[ \left( Q_{\phi_{target}}^{\pi_{\theta}} (s_{next}^{\prime}, a_{next}^{\prime}) \right] \right) \right)^2 \right]
\end{aligned}
$$
ここで,$\alpha, \beta$は適当なハイパーパラメタ,$d_{\widehat{\mathcal{M}}}$ は学習したモデル $\widehat{\mathcal{M}}$ 上での状態生成分布を表しています.また,最終項の期待値の部分は以下のように定義しています.
$$\mathbb{E}_{(s^{\prime}, a^{\prime}, s_{next}^{\prime}, r^{\prime}) \sim \widehat{\mathcal{M}}} \left[ \cdot \right] = \mathbb{E}_{s^{\prime} \sim d_{\widehat{\mathcal{M}}}(s^{\prime}), a^{\prime} \sim \pi_{\theta}(a^{\prime} \mid s^{\prime}), s_{next}^{\prime} \sim \mathcal{T}_{\widehat{\mathcal{M}}}(s_{next}^{\prime} \mid s^{\prime}, a^{\prime}), r^{\prime} \sim {P_r}_{\widehat{\mathcal{M}}}(r^{\prime} \mid s^{\prime}, a^{\prime})} \left[ \cdot \right]$$
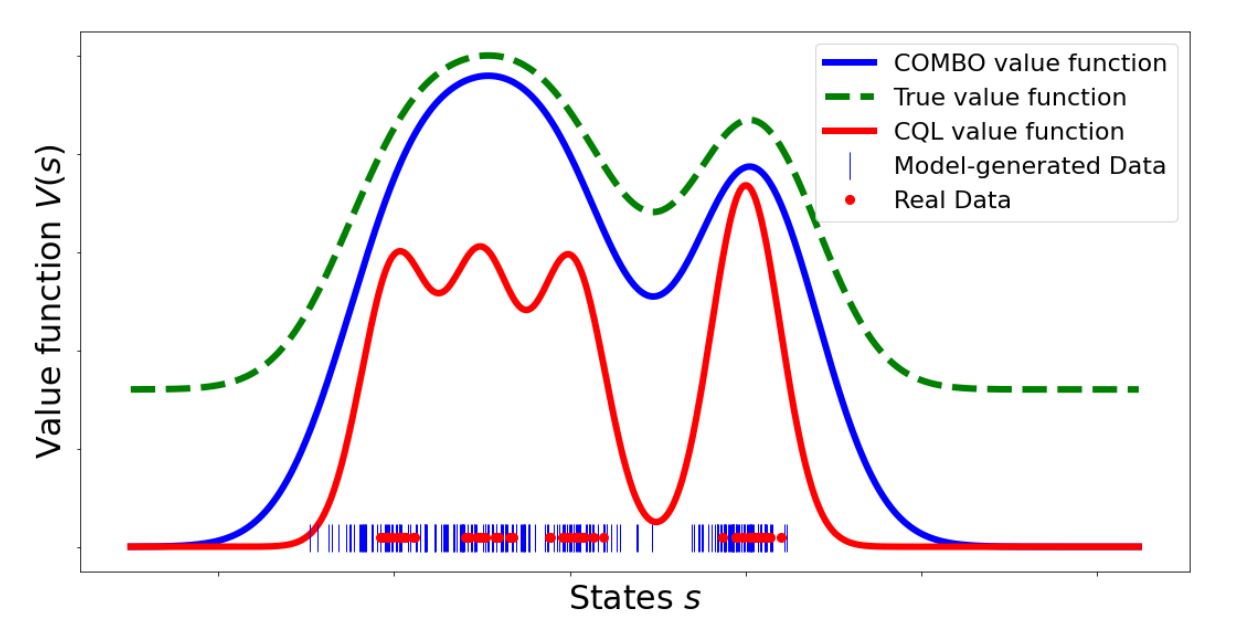
先程のCQLと比べてみると,1. の項が第一項の前半部分に,3. の項が第二項と第三項に置き換わっていることが分かります.直観的な説明をすれば,一般的なTD学習を表す第二項に対し,第三項はデータ拡張をしているとみることができ,学習したモデル $\widehat{\mathcal{M}}$ から得られるデータを一定量TD誤差学習に混ぜて汎化性を向上しています.一方,実データではない $\widehat{\mathcal{M}}$ から得られたデータはモデリングバイアスを含んでいたり不確実性が大きくなったりと信頼性は低いため,第一項でなるべく価値を保守的に見積もるようにし,過大評価を抑制しつつ汎化した価値学習が行えるようになっています.実際,COMBOはCQLよりもタイトな価値の推定下界を最大化する方策を獲得できることが理論的に示されています.
S4RL
S4RLはデータ拡張によりCQLの汎化性を向上させるもうひとつの,"surprisingly simple"な方法を提案しています[6-2].
$$
\begin{aligned}
\widehat{Q}^{\pi_{\theta}}_{\phi} & \leftarrow
\arg \min_{Q_{\phi}} \mathbb{E}_{(s_t, a_t, s_{t+1}, r_t) \sim \mathcal{D}} \left[ \alpha \left( \max_{\pi^{\prime}} \mathbb{E}_{a_t^{\prime} \sim \pi^{\prime}(a_t^{\prime} \mid s_t)} \left[ Q_{\phi} (s_t, a_t^{\prime}) \right] - Q_{\phi} (s_t, a_t) \right) \right. \
&+ \frac{1}{2} \left( \mathbb{E}_{DA(\widetilde{s}_t^{\prime} \mid s_t)} \left[ Q_{\phi}(\widetilde{s}_t^{\prime}, a_t) \right] - \left( r_t + \gamma \mathbb{E}_{DA(\widetilde{s}_{t+1}^{\prime} \mid s_{t+1})} \left[ \mathbb{E}_{a_{t+1}^{\prime} \sim \pi_{\theta}(a_{t+1}^{\prime} \mid \widetilde{s}_{t+1}^{\prime})} \left[ Q_{\phi_{target}}^{\pi_{\theta}} (\widetilde{s}_{t+1}^{\prime}, a_{t+1}^{\prime}) \right] \right] \right) \right)^2 \biggr]
\end{aligned}
$$
ここで,$\mathbb{E}_{DA(\widetilde{s}^{\prime} \mid s)} \left[ \cdot \right]$ はある状態 $s$ を適当なデータ拡張を行って $m$ 個の拡張データ $\widetilde{s}^{\prime}$ をサンプリングし,その期待値を取ったもの(経験平均)になっています.このデータ拡張は非常にシンプルであっても有効であり,例えば入力となる状態の画像データに対し,適当なガウスノイズなどでも汎化性が向上するという実験結果が報告されています.
まとめ
本記事で紹介したオフライン強化学習は,強化学習を過去に集めたデータのみを使って行うものであるため,オンラインで環境と作用する一般的な強化学習と比べてリスクが少なく,医療や自動運転などの実応用面で注目を集めていました.一方,オフライン強化学習では学習を全てオフラインで行うという性質により,unlearning effectと呼ばれる特有の技術的課題が存在していました.これは特に,behavior policyにより集められた偏ったデータで,かつ過去に異なる行動を取っていた場合の結果が分からないというデータの特性に起因して発生する分布シフトが原因になっていました.この問題をどう乗り越えていくかを考えるのがオフライン強化学習の大きなテーマでした.本記事では,オフライン強化学習において価値関数がうまく学習できない問題に対し,価値関数が仮にエラーを起こしたとしてもそのエラーの伝播と増幅を抑制する学習アルゴリズムである,CQLを紹介しました.さらに,その発展版のCOMBOやS4RLは,データ拡張を追加することでCQLの性能をさらに向上させていました.
未解決課題と今後の展望
最終章の本章では,これまでの流れを踏まえた上で,今後のオフライン強化学習の展望をまとめてみます.特に,オフライン強化学習の大きな枠組みの中でも筆者が個人的に興味をもっているトピックや未解決課題について紹介し,オフライン強化学習の面白さをお伝えして本記事を締めくくれたらと思います.なお,以降の話は,オフライン強化学習が比較的新しく,まだ体系立った分類が存在せず未解決課題も多い分野であることもあり(本記事執筆の2021年5月時点),かなり個人的な所感となっていることにご留意いただけたらと思います.
オフライン強化学習のひとつの方向性として個人的に面白そうだと思うのは,最後のCOMBOやS4RLでも行われていた,モデルベース強化学習の活用や自己教師あり学習を始めとした表現学習,それによるデータ拡張です.まず,モデルベース強化学習については,大きく分けてふたつの強みがあると考えています.ひとつ目は,モデルの学習自体は教師あり学習ライクに行えることです.モデルベース強化学習では状態遷移確率 $\mathcal{T}_{\widehat{\mathcal{M}}}(s_{next} \mid s, a)$ と ${P_r}_{\widehat{\mathcal{M}}}(r \mid s, a)$ の学習を行いますが,オフライン強化学習で使えるデータの組は $(s, a, s_{next}, r)$ であるためターゲットとなる教師データが存在している状況で生成モデルのフィッティングなどを行うことができます.ふたつ目の強みは,こうしてモデルが仮にうまく学習できた場合,この学習済みモデルは非常に安価なシミュレータとして使える点です.この学習済みモデルが活用できれば,例えばCOMBOのようにモデルをデータ拡張に使用したり,モデル上で方策をrolloutさせたりすることで,一般的な強化学習に比較的近い形でオフライン強化学習が行えるかもしれません.もちろん,良いシミュレータとして利用可能なモデルを学習するためにはモデルがout-of-distributionな状態や行動においても汎化した正確さを持つ必要があるという課題は残りますが,非常に可能性のある方向性だと思います.
そして,モデルを学習したり価値関数を学習したりする際の汎化性獲得において重要な役割を担うのが,自己教師あり学習をはじめとする表現学習や,獲得された表現によるデータ拡張なのではないかと考えています.例えばロボティクスのタスクなどにおいては画像ベースの入力を状態として扱うことも多いですが,これらのデータは多くの場合非常に高次元です.そのため,潜在的な特徴量をうまく抽出することで異なる状態間の類似性を考慮に入れた学習や,ノイズや環境の変化に頑健な学習に改善の余地がありそうです.また,沢山のデータを事前に集められるとは限らない医療などの文脈においても,データ拡張がうまく行えれば価値関数の学習を安定させられる可能性もあります.
関連する話題として,報酬が付与されていないデータも活用してモデルを学習できれば,よりデータ効率よく状態表現を獲得できるかもしれません.また,報酬の付与されていないデータで新たな方策の学習が行えれば,異なるタスクを行うbehavior policyにより集めたデータで別のタスクを行う方策を学習し習得できる可能性もあると思います.(例えば玉ねぎスープを作るデータとトマトカレーを作るデータを使って,トマトスープを作る方策を獲得するなど.また,クリック数最大化のための広告配信のログデータを使って費用対効果最大化の方策を獲得するなど.) 一般的に転移学習が難しいとされ,少し目的関数を変える毎にオンラインで追加的な(リスクを伴う)インタラクションが必要とされている強化学習の背景を踏まえると,オフラインで別タスクの学習が行えれば画期的な進展となるでしょう.実際,ロボティクスのタスクにおいて報酬が分からないデータに対し,入力となる状態間の距離をうまく表現学習することで,目標状態との距離を測ってオフライン強化学習する手法なども研究され始めており[7-1],非常に興味深い取り組みだと考えています.
さらに,一般的な強化学習ではよく「不確実なときは楽観的に」価値を見積もることにで探索を促進し,最終的に獲得できる方策下での期待報酬を高めようとしています.一方で,本記事での議論を振り返ると,オフライン強化学習では「不確実なときは悲観的に」価値を見積もる必要があることが分かると思います.このことから,オフライン強化学習はリスクを考慮した上で学習を行うという点において一般的な強化学習とは学習の仕方が大きく異なってきます.すなわち,オフライン強化学習においては,まだ見ぬ領域で期待報酬を最大化する方策を掘り当てようというよりは,報酬最大化を目指しつつも,まずはリスクが少ないデータの多い領域である程度の性能保証のありそうな着実な方策の獲得を目標にしているようにも思えます.これは,一般的な強化学習というよりもむしろ,模倣学習を彷彿とさせるアプローチでしょう.そのため,オフライン強化学習の文脈において模倣学習の知見も有用になるかもしれません.少し補足すると,模倣学習ではエキスパートデータと呼ばれる最適な(またはかなり最適に近い)データで主に学習を行いますが,オフライン強化学習ではエキスパートデータが使えるかどうかは分からないという点が異なっています.(behavior policyの性能が高いかどうかについての保証がなく,むしろbehavior policyの性能を上回るエージェントが獲得できると嬉しい) そこで,これらの違いを踏まえてどのように拡張するかがポイントになりそうです.
また,上記の模倣学習のように,一般的な強化学習はまた少し違う学習フレームワークという視点からオフライン強化学習の学習を考えてみるのも面白いと思います.例えば,一般的な強化学習では環境とのインタラクションによりデータ収集を行いながら方策を最適化するため,方策のアップデートと追加データによる価値の学習を交互に行っていました.しかし,追加的なデータが全く得られないオフライン強化学習においては,わざわざ方策のアップデートと価値関数の学習を交互に行う必要はあるのでしょうか?特に,unlearning effectの影響により学習ステップを増やすほど性能が悪化する可能性のあるオフライン強化学習においては,一考の価値がある問題だと思います.実際,R-BVEという手法では,behavior policyのtrajectory分布上において,データの少ない領域の価値を小さく見積もるように学習した後,方策のアップデートは最後に一回だけ行うことで十分に良い方策が得られるという実験結果を示しています[7-2].その一方で,モデルベース強化学習のMuZero Unpluggedというアプローチでは,モンテカルロ木探索と呼ばれる手法の活用によりオンラインとオフライン両方で良い性能を出すようなアルゴリズムも提案されています[7-3].一般的なオンラインとオフラインの強化学習がどのように異なり,果たして同じフレームワーク上で学習できるのかどうかは,これから議論の余地がありそうです.
他にも,今は強化学習は基本的には価値以外の部分に対してブラックボックスな状態で学習を行っていますが,人間が日常的に行っているようにtrajectoryの中で重要な分岐点は一体どこだったか,ある方策が良かった理由は何かなど,方策と最終的に得られた報酬の間における因果推論も有効であるかもしれません.また,同じように人間の学習における考察から考えてみると,やはり少ない回数であっても外的な(追加的な)フィードバックをもらえることは重要だと思われます.そのため,完全にオフラインで強化学習をするわけではなく,なるべく実環境とのインタラクションを減らしてリスクを抑えつつ,オンラインとオフラインを組み合わせたハイブリッドな学習方法を考えていくのもとても面白いと思います.例えば,AWACというアルゴリズムはオフラインで学習した後にオンラインでファインチューニングを行っています[7-4].これにより,最初から完全にオンラインで学習を行うより,実環境とのインタラクションの回数を減らし効率的に学習できるという実験結果が報告されています.また,新たな方策をアップデートし実環境にデプロイする回数に対しどれほど効率的に性能を向上させられているかを測る評価指標である"deployment-efficient"[7-5]などの視点も非常に面白そうです.
本章では,個人的なオフライン強化学習に対するワクワクをつらつらと書いてしまいました.長い文章になりましたが,最後まで読んでいただきありがとうございました.現在のオフライン強化学習はまだ単純なタスクで試されていることが大半で,実用にはほど遠く,未解決課題も沢山あると思います.しかし一方で,オフライン強化学習を使えると嬉しい実応用の場面は沢山あり,どのようにして今ある技術課題を克服して実用できるものにしていくのかという議論には,注目と期待が集まっています.筆者自身これからオフライン強化学習の文脈においてどのようなパラダイムシフトやブレイクスルーが起きるのか楽しみで,しばらくはキャッチアップ出来たらいいなと思っているところです.読んでくださった皆さんにも,なんとなく面白そう!と思っていただけていたら嬉しいです.
Appendix
最後に,興味を持っていただいた方に,本記事の元になった発表スライドなどいくつか紹介させていただこうと思います.
実は本記事を書く前に,強化学習若手の会でオフライン強化学習のチュートリアル発表をさせていただきました.本記事はその発表の際に全体の構成上省いたものの別の機会でもう少し話せたら良いなと思っていた,個人的に特に興味のあった内容についてまとめたものです.そのため,以下のスライドはもう少しさらっとした俯瞰的なまとめになっており,本記事では割愛した方策のオフライン評価(オフ方策評価) の話も含んでいます.また,後半の67ページあたりから始まる「もっといろいろ知りたい人へ」にまとめてあるマテリアルも参考になるかもしれません.興味ある方はぜひ見てみてください.
また,オフ方策評価に関しては,open bandit piplineという動かしながら学べる(主にバンディット設定でのオフ方策評価用の)ライブラリがおすすめです[8-1]. 特に,documentationに書かれているオフ方策評価についての導入的な説明や,多様な設定で充実したquickstartノートブックは新たに勉強し始めたい人にとって非常に有用なマテリアルになっていると思います.こちらもぜひチェックしてみてください.
open bandit pipeline
さらに,より発展的な内容について興味ある方向けに,オフライン強化学習とオフ方策評価について最新の論文やチュートリアル,講演動画など網羅的に集めたawesome-offline-rlというレポジトリを公開しています.本記事で紹介しきれなかった面白い研究が沢山載っているので,こちらもぜひご覧ください.
awesome-offline-rl
そして,もし関連する分野で面白い研究や論文知っているよ!という方がいらっしゃれば,ぜひ本記事へのコメントなどでご紹介いただけると嬉しいです.awesome-offline-rlへのpull requestもお待ちしています.
参考文献
全体的に
[1-1] Sergey Levine, Aviral Kumar, George Tucker, and Justin Fu. “Offline Reinforcement Learning: Tutorial, Review, and Perspectives on Open Problems”. arXiv preprint, 2020. [link]
[1-2] Richard S. Sutton and Andrew G. Barto. “Reinforcement learning: An introduction”. MIT press, 2018.
[1-3] 森村哲郎. MLP機械学習プロフェッショナルシリーズ強化学習. 講談社, 2019.
オフライン強化学習とは
[2-1] David Silver, Aja Huang, Chris J. Maddison, Arthur Guez, Laurent Sifre, George van den Driessche, Julian Schrittwieser, Ioannis Antonoglou, Veda Panneershelvam, Marc Lanctot, Sander Dieleman, Dominik Grewe, John Nham, Nal Kalchbrenner, Ilya Sutskever, Timothy Lillicrap, Madeleine Leach, Koray Kavukcuoglu, Thore Graepel, and Demis Hassabis. “Mastering the game of Go with deep neural networks and tree search”. Nature, 2016. [pdf]
[2-2] Jim Gao. “Machine Learning Applications for Data Center Optimization”. Google whitepaper, 2016. [pdf]
[2-3] Wenshuai Zhao, Jorge Peña Queralta, and Tomi Westerlund. “Sim-to-Real Transfer in Deep Reinforcement Learning for Robotics: a Survey”. SSCI, 2020. [link]
一般的な強化学習を振り返る
[3-1] Tuomas Haarnoja, Aurick Zhou, Pieter Abbeel, and Sergey Levine. “Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor”. ICML, 2018. [link]
[3-2] Benjamin Eysenbach and Sergey Levine. “Maximum Entropy RL (Provably) Solves Some Robust RL Problems”. arXiv, 2021. [link]
なぜ単純な拡張ではだめなのか?
[4-1] A. Kumar. “Data-Driven Deep Reinforcement Learning”. BAIR blog, 2019. [link]
[4-2] Aviral Kumar, Justin Fu, George Tucker, and Sergey Levine. “Stabilizing Off-Policy Q-Learning via Bootstrapping Error Reduction”. NeurIPS, 2019. [link]
[4-3] Hado van Hasselt, Yotam Doron, Florian Strub, Matteo Hessel, Nicolas Sonnerat, and Joseph Modayil. “Deep Reinforcement Learning and the Deadly Triad”. arXiv, 2018. [link]
Conservative Q-Learning
[5-1] Aviral Kumar, Aurick Zhou, George Tucker, and Sergey Levine. “Conservative Q-Learning for Offline Reinforcement Learning”. ICML, 2020. [link]
[5-2] Natasha Jaques, Asma Ghandeharioun, Judy Hanwen Shen, Craig Ferguson, Agata Lapedriza, Noah Jones, Shixiang Gu, and Rosalind Picard. “Way Off-Policy Batch Deep Reinforcement Learning of Implicit Human Preferences in Dialog”. arXiv preprint, 2019. [link]
[5-3] Yifan Wu, George Tucker, and Ofir Nachum. “Behavior Regularized Offline Reinforcement Learning”. arXiv preprint, 2019. [link]
[5-4] Ian Osband, Charles Blundell, Alexander Pritzel, and Benjamin Van Roy. “Deep Exploration via Bootstrapped DQN”. NeurIPS, 2016. [link]
CQLの発展版
[6-1] Tianhe Yu, Aviral Kumar, Rafael Rafailov, Aravind Rajeswaran, Sergey Levine, and Chelsea Finn. “COMBO: Conservative Offline Model-Based Policy Optimization”. arXiv, preprint, 2021. [link]
[6-2] Samarth Sinha and Animesh Garg. “S4RL: Surprisingly Simple Self-Supervision for Offline Reinforcement Learning”. arXiv preprint, 2021. [link]
今後の展望とオフライン強化学習の面白さ
[7-1] Stephen Tian, Suraj Nair, Frederik Ebert, Sudeep Dasari, Benjamin Eysenbach, Chelsea Finn, and Sergey Levine. “Model-Based Visual Planning with Self-Supervised Functional Distances”. ICLR, 2021. [link]
[7-2] Caglar Gulcehre, Sergio Gómez Colmenarejo, Ziyu Wang, Jakub Sygnowski, Thomas Paine, Konrad Zolna, Yutian Chen, Matthew Hoffman, Razvan Pascanu, and Nando de Freitas. “Regularized Behavior Value Estimation”. arXiv preprint, 2021. [link]
[7-3] Julian Schrittwieser, Thomas Hubert, Amol Mandhane, Mohammadamin Barekatain, Ioannis Antonoglou, and David Silver. “Online and Offline Reinforcement Learning by Planning with a Learned Model”. arXiv preprint, 2021. [link]
[7-4] Ashvin Nair, Abhishek Gupta, Murtaza Dalal, and Sergey Levine. “AWAC: Accelerating Online Reinforcement Learning with Offline Datasets”. arXiv preprint, 2020. [link]
[7-5] Tatsuya Matsushima, Hiroki Furuta, Yutaka Matsuo, Ofir Nachum, and Shixiang Gu. “Deployment-Efficient Reinforcement Learning via Model-Based Offline Optimization”. ICLR, 2021. [link]
Appendix
[8-1] Yuta Saito, Shunsuke Aihara, Megumi Matsutani, and Yusuke Narita. “Open Bandit Dataset and Pipeline: Towards Realistic and Reproducible Off-Policy Evaluation”. arXiv preprint, 2020. [link]