数理最適化問題のチートシート的なもの (3) - 線形計画・凸2次計画の続きです。
5. 半正定値計画
5.1 半正定値計画問題
対称行列 $X\in S^n$ を変数とする以下のような最適化問題。変数がベクトルではなく対称行列である点、その半正定値性を制約として含むことが特徴。
\begin{array}
&\displaystyle\min_{X\in S^n} &C\cdot X \\
s.t. &A_i\cdot X=b_i, &i=1,\cdots,m \\
&X\succeq O
\end{array}
双対問題は以下。双対問題もまた半正定値計画問題であり、適当な変換を施すことで主問題と同様の形式に変換することができる。
\begin{array}
&\max &\displaystyle\sum_{i=1}^{m}b_iy_i \\
s.t. &\displaystyle\sum_{i=1}^{m}y_iA_i+S=C \\
&S\succeq O
\end{array}
半正定値対称行列の集合 $S_+^n$ は自己双対錐である。主問題と双対問題の形式が一致するという性質は、この自己双対性に由来する。また、比較的緩い仮定の下で、主問題と双対問題の最適値が一致するという双対性を持つ。これらは、内点法の基礎となる特徴である。
自己双対錐には、非負ベクトルの集合 $\mathbb{R}^n_+=\lbrace\boldsymbol{x}\in\mathbb{R}^n~|~\boldsymbol{x}\geq\boldsymbol{0}\rbrace$ や2次錐などが知られている。自己双対錐に関連する問題には以下のようなものがある。
- 線形計画問題:錐 $\mathbb{R}^n$ と線形の等式を制約として線形関数を最小化する問題
- 2次錐計画問題:2次錐と線形の等式を制約として線形関数を最小化する問題
なお、一般の最適化問題では、双対問題は必ずしも主問題と同じ形式の問題になるとは限らないし、双対性が成り立つとも限らない。
さまざまな問題を半正定値計画問題として定式化するのにしばしば有効なのが、Schurの補元に関する次の性質。
行列 $A, B, C$ に対して、$Z$ を以下のように定義する。$A\succeq O$ のとき、条件 $Z\succeq O$ と条件 $B-C^TA^{-1}C\succeq O$ とは同値である。
Z=
\begin{bmatrix}
A & C \\
C^T & B
\end{bmatrix}
上記の性質を用いて凸2次計画や凸2次制約を含む問題を半正定値計画に変換することが可能。例えば以下。$\displaystyle t \geq \frac{1}{2}\boldsymbol{x}^T Q\boldsymbol{x}+\boldsymbol{c}^T\boldsymbol{x}$ を線形行列不等式に置き換えている。ただし、$LL^T = Q$。
\begin{array}
&\min &\displaystyle\frac{1}{2}\boldsymbol{x}^T Q\boldsymbol{x}+\boldsymbol{c}^T\boldsymbol{x} \\
s.t. &A\boldsymbol{x}\leq\boldsymbol{b}
\end{array}
\iff
\begin{array}
&\min &t \\
s.t. &\begin{bmatrix}
\displaystyle\frac{1}{2}I & L^T\boldsymbol{x} \\
\boldsymbol{x}^T L & -\boldsymbol{c}^T\boldsymbol{x}-t
\end{bmatrix}
\succeq O \\
&A\boldsymbol{x}\leq\boldsymbol{b}
\end{array}
以下のS補題はFarkasの補題の2次不等式への拡張とも言える重要な命題。
$A, B\in S^n$ を定行列とし、条件 $\hat{\boldsymbol{y}}^T A\hat{\boldsymbol{y}}>0$ を満たす $\hat{\boldsymbol{y}}\in\mathbb{R}^n$ が存在することを仮定すると、以下の2つの条件は同値である。
(a) $B-\tau A\succeq O,~\tau\geq 0$ を満たす $\tau\in\mathbb{R}$ が存在する。
(b) $\boldsymbol{y}^T A\boldsymbol{y}\geq 0$ を満たす任意の $\boldsymbol{y}$ に対して $\boldsymbol{y}^T B\boldsymbol{y}\geq 0$ が成立する。
5.2 双対性と内点法
5.2.1 双対定理
以下のとおり弱双対性が成り立つ。
\displaystyle C\cdot X-\boldsymbol{b}^T\boldsymbol{y}=\left(\sum_{i=1}^{m}y_iA_i+S\right)\cdot X-\sum_{i=1}^{m}\left(A_i\cdot X\right)y_i=X\cdot S\geq 0
また、以下のとおり強双対性が成り立つ。
- 主問題と双対問題の両方に、内点実行可能解が存在することを仮定する。このとき、それぞれの問題に最適解が存在する。また、実行可能解 $X$ および $(\boldsymbol{y}, S)$ がそれぞれの問題の最適解であるための必要十分条件は、主問題と双対問題の目的関数値が一致すること、すなわち $X\cdot S=0$ である。
主問題と双対問題に内点実行可能解が存在するとき、最適解の必要十分条件は以下。
\begin{array}
~A_i\cdot X=b_i,~~~~~i=1,\cdots,m \\
\displaystyle\sum_{i=1}^{m}y_iA_i+S=C \\
XS=O \\
X\succeq O,~~S\succeq O
\end{array}
線形計画問題を最適性条件を行列に拡張したような形。3つ目と4つ目の条件は、直交行列 $Q$ を用いて固有値分解できて、固有値 $\lambda_j$ および $\omega_j$ が以下を満たすことと同値。
\lambda_j\geq 0,~~~~\omega_j\geq 0,~~~~\lambda_j\omega_j=0,~~~~~j=1,\cdots,n
5.2.2 半正定値計画問題のスケーリング
半正定値計画問題は、正則行列 $P\in\mathbb{R}^{n\times n}$ を1つ固定して線形変換を行っても等価な問題となる。
\tilde{X}=P^{-1} X{P^{-1}}^T,~~\tilde{A}_i=P^T A_iP,~~\tilde{\boldsymbol{y}}=\boldsymbol{y},~~\tilde{S}=P^T SP
5.2.3 半正定値計画問題の内点法
半正定値計画問題の代表的な解法は内点法。主内点法や主双対内点法があり、特に主双対内点法は実用も多い重要な解法。
バリア関数を $X$ の行列式に対して定義して、以下のような最適化問題を考える。
\begin{array}
&\displaystyle\min_{X\in S^n} &C\cdot X-\nu\log (\det X) \\
s.t. &A_i\cdot X=b_i, &i=1,\cdot,m \\
&X\succeq O
\end{array}
双対問題に対しても同様に、バリア関数を付加した最適化問題を考える。
\begin{array}
&\max &\displaystyle\sum_{i=1}^{m}b_iy_i+\nu\log (\det S) \\
s.t. &\displaystyle\sum_{i=1}^{m}y_iA_i+S=C \\
&S\succeq O
\end{array}
これらの最適性条件は以下。
\begin{array}
~A_i\cdot X=b_i,~~~~~i=1,\cdots,m \\
\displaystyle\sum_{i=1}^{m}y_iA_i +S=C \\
XS=\nu I \\
X\succeq O,~~S\succeq O
\end{array} \tag{5-1} \label{5.24}
初期点を $(X_0,\boldsymbol{y}_0,S_0)$ とし、順次以下の式に従って解を更新する。
\begin{array}
~X_{k+1}=X_k+\alpha_k\Delta X \\
\boldsymbol{y}_{k+1}=\boldsymbol{y}_k+\alpha_k\Delta\boldsymbol{y} \\
S_{k+1}=S_k+\alpha_k\Delta S
\end{array}
$k$ 回目の反復で得られている点 $ (X_k,\boldsymbol{y}_k,S_k) $ に対する双対性ギャップの尺度 $\rho_k$ を以下のとおり定義する。中心曲線上では $\rho_k=\nu$。
\displaystyle\rho_k = \frac{X_k\cdot S_k}{n}
$k+1$ 回目の点における $\nu_{k+1}$ の目標値を定数 $\gamma\in (0,1)$ を用いて以下のとおり定める。
\nu_{k+1}=\gamma\rho_k
式 ($\ref{5.24}$) で $\nu=\nu_{k+1}$ とおいた式を線形近似して解き、探索方向 $(\Delta X,\Delta\boldsymbol{y},\Delta S)$ とし、適当なステップ幅 $\alpha_k$ を定めて次の点に移る。
なお、式 ($\ref{5.24}$) で $\nu=\nu_{k+1}$ とおき線形近似した方程式は、式の本数が変数の数より多いため、解をもつとは限らないという問題点がある。解決策として、3本目の式を以下のように緩和する方法がある。
XS+SX=2\nu I
5.4 2次錐計画
5.4.1 2次錐計画問題
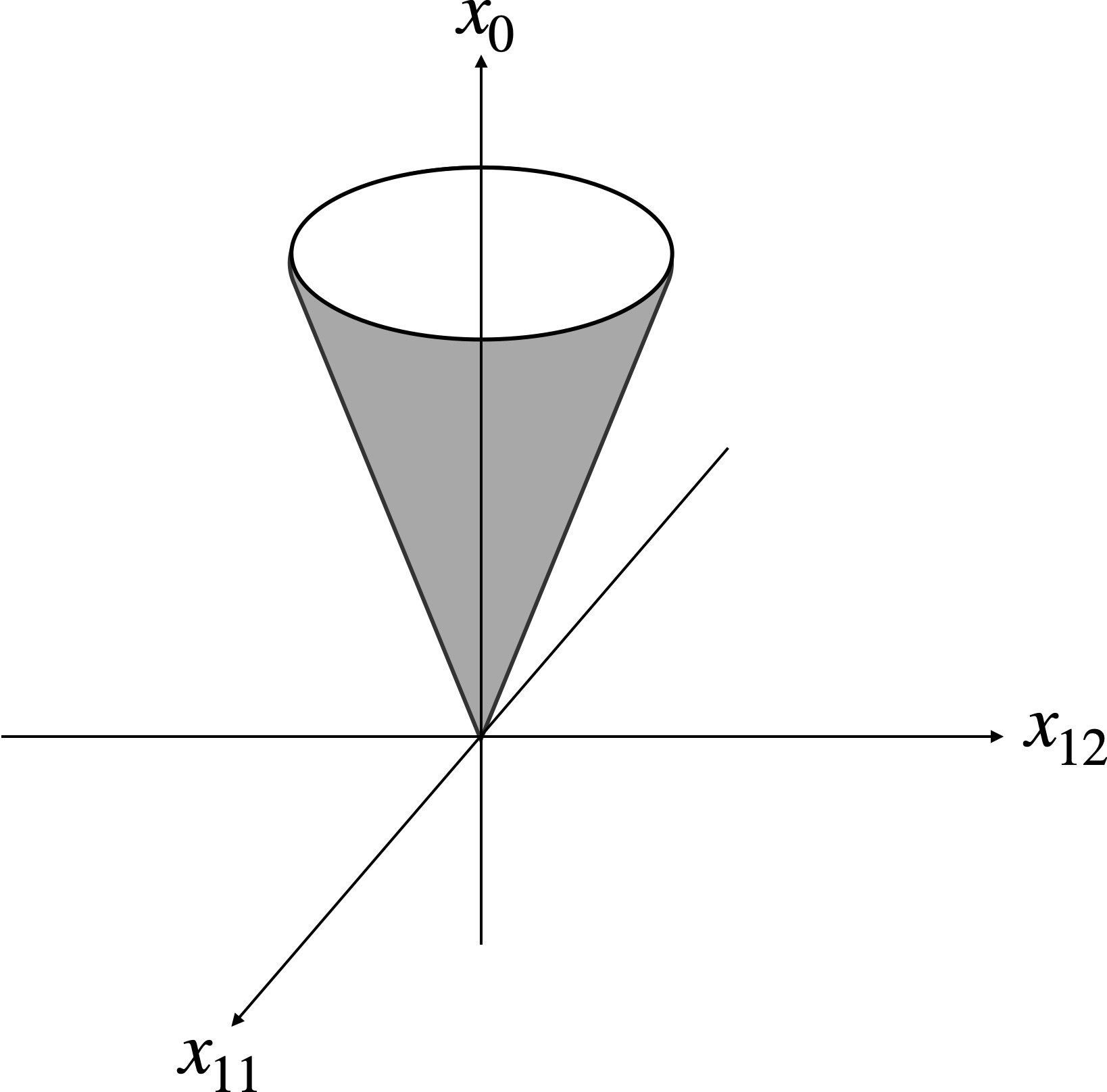
スカラー $x_0$ とベクトル $\boldsymbol{x}_1\in\mathbb{R}^{n-1}$ に対して定義される以下の集合を $n$ 次元の2次錐と呼ぶ。
L^n=\lbrace\left(x_0,\boldsymbol{x}_1\right)~|~\boldsymbol{x}\geq\|\boldsymbol{x}_1\|\rbrace
$n=3$ のときの2次錐は以下のイメージ。
条件 $\boldsymbol{x}\in L^n$ を2次錐制約と呼び、いくつかの2次錐制約と線形の等式制約の下で線形の目的関数を最小化する最適化問題を、2次錐計画問題と呼ぶ。
\begin{array}
&\min &\displaystyle\sum_{l=1}^{r}\boldsymbol{c}_l^T\boldsymbol{x}_l \\
s.t. &\displaystyle\sum_{l=1}^{r}A_l\boldsymbol{x}_l=\boldsymbol{b} \\
&x_{l0}\geq\|\boldsymbol{x}_{l1}\|, &l=1,\cdots,r
\end{array}
双対問題は以下。双対問題も2次錐計画問題。2次錐計画問題は半正定値計画問題なので当然。弱双対性・強双対性も成り立つ。
\begin{array}
&\max &\boldsymbol{b}^T\boldsymbol{y} \\
s.t. &A_l^T\boldsymbol{y}+\boldsymbol{s}_l=\boldsymbol{c}_l, &l=1,\cdots,r \\
&s_{l0}\geq\|\boldsymbol{s}_{l1}\|, &l=1,\cdots,r
\end{array}
最適性条件は以下。
\begin{array}
~\displaystyle\sum_{l=1}^{r}A_l\boldsymbol{x}_l=\boldsymbol{b} \\
A_l^T\boldsymbol{y}+\boldsymbol{s}_l=\boldsymbol{c}_l,~~~~~l=1,\cdots,r \\
x_{l0}s_{l0}+\boldsymbol{x}_{l1}^T\boldsymbol{s}_{l1}=0,~~~~~l=1,\cdots,r \\
x_{l0}\geq\|\boldsymbol{x}_{l1}\|,~~~s_{l0}\geq\|\boldsymbol{s}_{l1}\|,~~~~~l=1,\cdots,r
\end{array}
相補性条件を書き下すと以下。2次錐制約のうちいずれか一方が非有効であればもう一方の変数はゼロベクトルになることを表している。
\begin{array}
&x_{l0}>\|\boldsymbol{x}_{l1}\|, &\left(s_{l0},\boldsymbol{s}_{l1}\right)=\left(0,\boldsymbol{0}\right) \\
\left(x_{l0},\boldsymbol{x}_{l1}\right)=\left(0,\boldsymbol{0}\right), &s_{l0}>\|\boldsymbol{s}_{l1}\| \\
x_{l0}=\|\boldsymbol{x}_{l1}\|, &s_{l0}=\|\boldsymbol{s}_{l1}\|, &\|x_{l1}\|\|\boldsymbol{s}_{l1}\|+\boldsymbol{x}_{l1}^T\boldsymbol{s}_{l1}=0
\end{array}
5.4.2 2次錐計画問題の解法
内点法。特に主双対内点法。
主問題にバリア関数を組み込んだ以下の最適化問題を考える。
\begin{array}
&\min &\displaystyle\sum_{l=1}^{r}\boldsymbol{c}_l^T\boldsymbol{x}_l-\frac{\nu}{2}\sum_{l=1}^{r}\log\left(x_{l0}^2-\|\boldsymbol{x}_{l1}\|^2\right) \\
s.t. &\displaystyle\sum_{l=1}^{r}A_l\boldsymbol{x}_l=\boldsymbol{b} \\
&x_{l0}>\|\boldsymbol{x}_{l1}\|, &l=1,\cdots,r
\end{array}
この問題の最適性条件は以下。
\begin{array}
~\displaystyle\sum_{l=1}^{r}A_l\boldsymbol{x}_l=\boldsymbol{b} \\
A_l^T\boldsymbol{y}+\boldsymbol{s}_l=\boldsymbol{c}_l,~~~~~l=1,\cdots,r \\
\begin{bmatrix}
x_{l0}s_{l0}+\boldsymbol{x}_{l1}^T\boldsymbol{s}_{l1} \\
s_{l0}\boldsymbol{x}_{l1}+x_{l0}\boldsymbol{s}_{l1}
\end{bmatrix}
=\nu\begin{bmatrix}
1 \\
\boldsymbol{0}
\end{bmatrix}
,~~~~~l=1,\cdots,r \\
x_{l0}>\|\boldsymbol{x}_{l1}\|,~~~s_{l0}>\|\boldsymbol{s}_{l1}\|,~~~~~l=1,\cdots,r
\end{array}
上記方程式を解いて探索方向を決定して、解を更新する。今までの主双対内点法と一緒なので省略。