数理最適化問題のチートシート的なもの (2) - 双対理論の続きです。
4. 線形計画
4.1 線形計画問題
4.1.1 定義
いくつかの線形方程式や線形不等式を制約とし、線形関数を目的関数とする最適化問題。
\begin{array}
&\min &\sum_{j=1}^{n}c_jx_j \\
s.t. &\boldsymbol{a}_i^T\boldsymbol{x}=b_i, &i=1,\cdots,m \\
&x_j\geq 0, &j=1,\cdots,n
\end{array}
より簡潔な表記として以下がある。どのような線形計画問題も、適当な変形をすることで以下の形に書き直せる。
\begin{array}
&\min &\boldsymbol{c}^T\boldsymbol{x} \\
s.t. &A\boldsymbol{x}=\boldsymbol{b} \\
&\boldsymbol{x}\geq\boldsymbol{0}
\end{array} \tag{4-1} \label{4.2}
4.2 双対性
4.2.1 双対問題
主問題 ($\ref{4.2}$) に対して、以下の問題を双対問題という。
\begin{array}
&\max &\boldsymbol{b}^T\boldsymbol{y} \\
s.t. &A^T\boldsymbol{y}\leq\boldsymbol{c}
\end{array} \tag{4-2} \label{4.11}
スラック変数 $\boldsymbol{s}$ を導入して以下のようにも書ける。
\begin{array}
&\max &\boldsymbol{b}^T\boldsymbol{y} \\
s.t. &A^T\boldsymbol{y}+\boldsymbol{s}=\boldsymbol{c} \\
&\boldsymbol{s}\geq\boldsymbol{0}
\end{array}
線形計画では、双対問題の双対問題は主問題。
4.2.2 双対定理
以下のとおり弱双対定理が成り立つ。以下の性質を弱双対性という。
主問題 ($\ref{4.2}$) の任意の実行可能解 $\boldsymbol{x}$ と双対問題 ($\ref{4.11}$) の任意の実行可能解 $\boldsymbol{y}$ に対して、以下の不等式が成り立つ。
\boldsymbol{c}^T\boldsymbol{x}\geq\boldsymbol{b}^T\boldsymbol{y}
また、以下のとおり強双対定理が成り立つ。以下の性質を強双対性という。ファルカスの補題を使って証明できる。
主問題 ($\ref{4.2}$) と双対問題 ($\ref{4.11}$) がともに実行可能解を持つことと、両者に最適解が存在して最適値が一致することとは、同値である。
4.2.3 最適性条件
以下のとおり相補性定理が成り立つ。以下の条件を相補性条件という。
主問題 ($\ref{4.2}$) の実行可能解 $\boldsymbol{x}$ と双対問題 ($\ref{4.11}$) の実行可能解 $\boldsymbol{y}$ がそれぞれの問題の最適解であるための必要十分条件は、以下の条件が成り立つことである。
x_j(\boldsymbol{c}-A^T\boldsymbol{y})_j=0,~~~~~j=1,\cdots,n
最適解においては、主問題の不等式制約 $x_j\geq 0$ と双対問題の不等式制約 $(\boldsymbol{c}-A^T\boldsymbol{y})_j\geq 0$ の少なくとも一方が有効になることを表している。
また、以下が成り立つとき、解 $\boldsymbol{x}$ と $\boldsymbol{y}$ は狭義相補性を満たすという。主問題の不等式制約と双対問題の不等式制約のどちらか一方のみ有効になることを示している。
x_j(\boldsymbol{c}-A^T\boldsymbol{y})_j>0,~~~~~j=1,\cdots,n
最適解 $\boldsymbol{x}$ と $\boldsymbol{y}$ が狭義相補性を満たすとき、相補性条件から以下の連立方程式が得られ、最適解はその解となる。ただし、$N, B$ は未知なので、方程式を解けば解が求まるというわけではない点に注意。適当な $N, B$ を見つける問題になる (cf. 単体法)。
\begin{array}
&x_j=0, &j\in N \\
(\boldsymbol{c}-A^T\boldsymbol{y})_j=0, &j\in B
\end{array}
ただし、$N, B$ は $\lbrace 1,\cdots,n\rbrace$ の部分集合で $N\cup B =\lbrace 1,\cdots,n\rbrace$ および $N\cap B$ を満たす。
主問題・双対問題それぞれの最適解であるための必要十分条件は以下。
\begin{array}
&A\boldsymbol{x}=\boldsymbol{b} \\
A^T\boldsymbol{y}+\boldsymbol{s}=\boldsymbol{c} \\
x_js_j=0,~~~~~j=1,\cdots,n \\
\boldsymbol{x}\geq\boldsymbol{0},~~~~~\boldsymbol{s}\geq\boldsymbol{0}
\end{array}
4.3 単体法
実行可能基底解と呼ばれる点、すなわち実行可能領域の頂点を順々に辿ることで線形計画問題の最適解を得る方法。
4.3.1 基底解
$A$ の列を適当に並び替え、それに伴ってそれに伴って $\boldsymbol{x}$ の行も並び替え、以下のようにする。
A=\begin{bmatrix}
A_B~|~A_N
\end{bmatrix},~~~~~\boldsymbol{x}=\begin{bmatrix}
\boldsymbol{x}_B \\
\boldsymbol{x}_N
\end{bmatrix}
以下で定義されるベクトル $\hat{\boldsymbol{x}}$ を基底解と呼ぶ。基底解は等式制約を満たす。
\hat{\boldsymbol{x}}=\begin{bmatrix}
\hat{\boldsymbol{x}}_B \\
\hat{\boldsymbol{x}}_N
\end{bmatrix}=\begin{bmatrix}
A_B^{-1}\boldsymbol{b} \\
\boldsymbol{0}
\end{bmatrix}
$\hat{\boldsymbol{x}}_B\geq\boldsymbol{0}$ を満たす場合実行可能基底解と呼ぶ。実行可能領域の頂点を表す。
また、$\hat{\boldsymbol{x}}_B>\boldsymbol{0}$ のとき $\hat{\boldsymbol{x}}$ は非退化であるといい、そうでないとき退化しているという。
同様に $\boldsymbol{c}, \boldsymbol{s}$ も分割し、$\hat{\boldsymbol{y}}, \hat{\boldsymbol{s}}$ を以下のように定義する。
\begin{array}
&\hat{\boldsymbol{y}}=(A_B^{-1})^T\boldsymbol{c}_B \\
\hat{\boldsymbol{s}}_B=\boldsymbol{0} \\
\hat{\boldsymbol{s}}_N=\boldsymbol{c}_N-A_N^T(A_B^{-1})^T\boldsymbol{c}_B
\end{array}
以上で定義した $\hat{\boldsymbol{x}}$ と $(\hat{\boldsymbol{y}}, \hat{\boldsymbol{s}})$ は $\hat{\boldsymbol{s}}_N\geq\boldsymbol{0}$ のとき最適性条件を満たすため、主問題・双対問題の最適解となる。適当な $N, B$ を探すのが、単体法でやっていること。
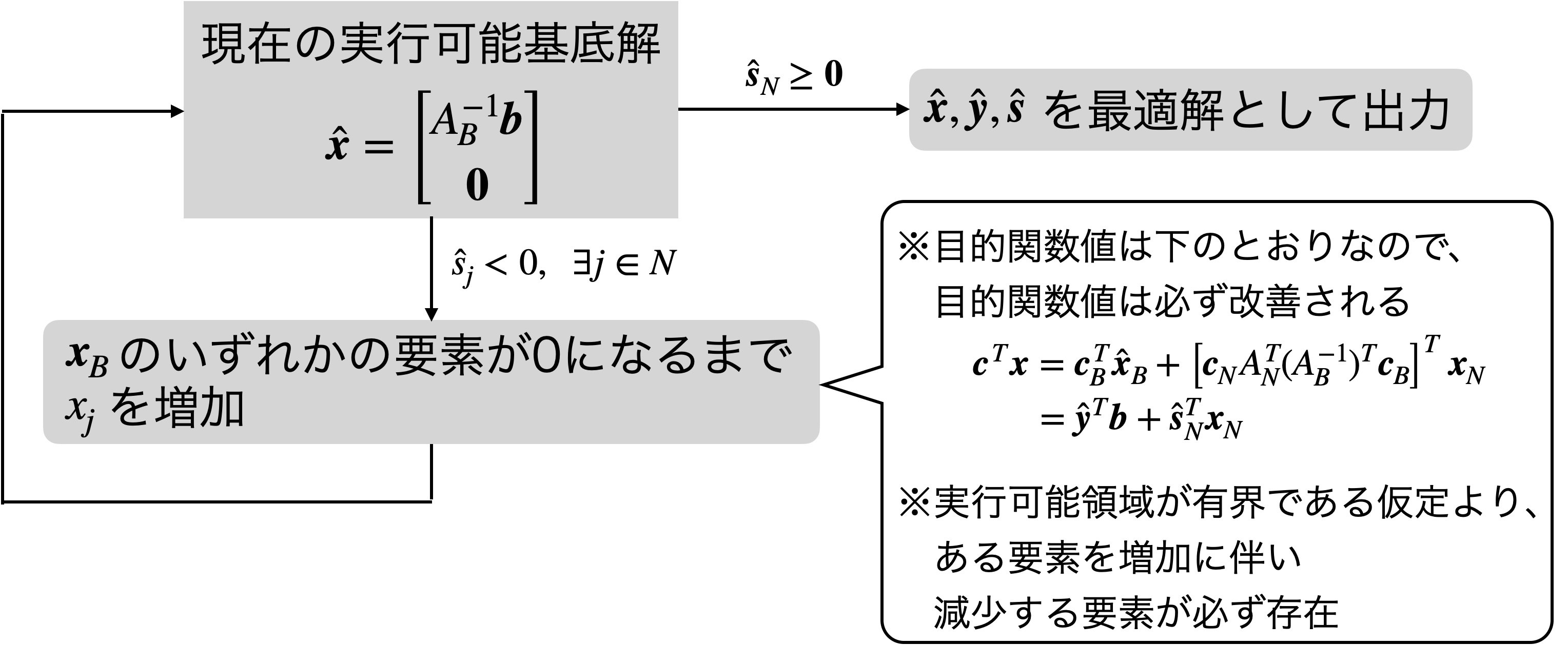
4.3.2 枢軸変換 (非退化な問題の場合)
主問題のすべての実行可能基底解が非退化であること (非退化仮定) と実行可能領域が有界であることを仮定した場合の手法。
1つの実行可能基底解から新しい実行可能基底解を生成する変換を枢軸変換という。以下の図の処理。
4.3.3 退化した問題の場合
非退化仮定が成り立たない場合、退化が繰り返し発生して同じ基底解に戻ってしまう現象 (巡回) が起こりうる。
枢軸変換における $x_j$ などの選び方を工夫することによって、単体法が有限回で終了し最適解が得られることが知られている。
具体的には、最小添字規則や辞書式規則がある。
4.3.4 2段階単体法
4.3.2節の枢軸変換は、主問題の実行可能基底解が分かっているときの手法。2段階単体法では、初期解となる実行可能基底解を見つけるために、まず別の線形計画問題を単体法で解くという方法。
第1段階では、以下の条件を満たす補助問題を作る。
①実行可能基底解のうちの1つが自明に分かっている
②最適解から主問題の実行可能基底解の情報が得られる。
例えば、以下のような問題。$\boldsymbol{x}_a$ は人工変数と呼ばれる。
\begin{array}
&\min &\boldsymbol{1}^T\boldsymbol{x}_a \\
s.t. &A\boldsymbol{x}+\boldsymbol{x}_a=\boldsymbol{b} \\
&\boldsymbol{x}\geq\boldsymbol{0},~~~~\boldsymbol{x}_a\geq\boldsymbol{0}
\end{array}
この問題は実行可能基底解 $(\boldsymbol{x},\boldsymbol{x}_a)=(\boldsymbol{0},\boldsymbol{b})$ をもち、得られた最適値が正の場合は、元の問題は実行可能解を持たない。逆に得られた最適値が0で最適解が $\boldsymbol{x}_a=\boldsymbol{0}$ を満たしていれば、そのときの $\boldsymbol{x}$ は元の問題の実行可能基底解となっているため、それを初期解として、元の問題に対して単体法を実行すればよい。
4.3.5 その他の単体法
- 双対単体法:線形計画問題の双対問題を解くことによって主問題の最適解を得る単体法。(主) 単体法は双対問題の制約と相補性条件を前提として主問題の制約を満たすような解を探す方法である一方、双対単体法は主問題の制約と相補性条件を前提として双対問題の制約を満たすような解を探す方法であると言える。
- ネットワーク単体法:$A$ がグラフの接続行列である場合は基底解をグラフ上の木と対応させることができるという性質を利用することで、効率的に単体法を実行する方法。
4.4 内点法
最適解に収束する内点実行可能解 (条件 $\boldsymbol{x}\geq\boldsymbol{0}$ および $\boldsymbol{s}\geq\boldsymbol{0}$ を満たす実行可能解) の点列を生成する解法であり、大規模な線形計画問題を解く際には単体法より優れているとされている。また、半正定値計画問題や2次錐計画問題などに一般化されている。
主問題の空間で点列を生成する主内点法と、主問題および双対問題の両方の空間に点列を生成する双対内点法とがある。
4.4.1 線形計画問題のサイズ
線形計画問題 ($\ref{4.2}$) において $A, \boldsymbol{b}, \boldsymbol{c}$ の各要素が整数であるとき、問題のサイズ $L$ は以下のとおり定義される。
L=\sum_{i=1}^{m}\sum_{j=1}^{n}\lceil\log_2 (|A_{ij}|+1)\rceil +\sum_{i=1}^{m}\lceil\log_2 (|b_i|+1)\rceil + \sum_{j=1}^{n}\lceil\log_2 (|c_j|+1)\rceil + mn+1
線形計画問題を解くために必要なビット演算の回数が $L, m, n$ の多項式で抑えられるアルゴリズムを、線形計画問題に対する多項式時間アルゴリズムという。
また、線形計画問題のサイズ $L$ を用いて、最適解の大きさや最適値について以下のとおり評価できる。
- 主問題 ($\ref{4.2}$) および双対問題 ($\ref{4.11}$) に最適解が存在するならば、最適解の中には $x_1,\cdots,x_n,y_1,\cdots,y_m$ の絶対値がすべて $2^L$ 以下のものが存在する。
- 主問題 ($\ref{4.2}$) および双対問題 ($\ref{4.11}$) に対して最適値との差が $2^{-L}$ 以下の近似解が得られたら、その近似解を利用して厳密解を多項式時間で求めることができる。
4.4.2 主内点法
以下のように、主問題 ($\ref{4.2}$) に対しバリア関数を用いて定義される凸最適化問題を解きつつ、$\nu→+0$ として最適解に迫る手法。
\begin{array}
&\min &\boldsymbol{c}^T\boldsymbol{x}-\nu\sum_{j=1}^{n}\log x_j \\
s.t. &A\boldsymbol{x}=\boldsymbol{b} \\
&\boldsymbol{x}>\boldsymbol{0}
\end{array}
上記の問題は $\boldsymbol{x}>\boldsymbol{0}$ を明に考えなくてよいので、等式制約のみの問題として扱える。ラグランジュ乗数法を使えば、無制約の最適化問題となるので、ニュートン法で解ける。
4.4.3 主双対内点法
主問題 ($\ref{4.2}$) および双対問題 ($\ref{4.11}$) の最適性条件に正のパラメータ $\nu$ を導入した以下の方程式を解きつつ、$\nu→+0$ として最適解に迫る方法。
\begin{array}
~A^T\boldsymbol{y}+\boldsymbol{s}=\boldsymbol{c} \\
x_js_j=\nu,~~~~j=1,\cdots,n \\
\boldsymbol{x}>\boldsymbol{0},~~\boldsymbol{s}>\boldsymbol{0}
\end{array} \tag{4-3} \label{4.37}
$k$ 回目の反復における点 $\left(\boldsymbol{x}_k,\boldsymbol{y}_k,\boldsymbol{s}_k\right)$ に対する双対性ギャップの尺度 $\rho_k$ を以下のとおり定義。
\rho_k=\frac{\boldsymbol{x}_k^T\boldsymbol{s}_k}{n}
$k$ 回目の反復における点が中心曲線上にあれば $\rho_k=\nu$ だが、実際は中心曲線上とは限らないため、$\rho_k$ は $\nu$ の近似値的な役割を果たす。中心曲線を $\nu$ が減少する方向に辿りたいため、次の点における $\nu$ の目標値 $\nu_{k+1}$ を以下のとおり定める ($0\leq\gamma<1$)。
\nu_{k+1}=\gamma\rho_k
そして、式 ($\ref{4.37}$) で $k+1$ 回目の点について、$\nu=\nu_{k+1}$ とおいた次の方程式の解 $(\Delta\boldsymbol{x}$,$\Delta\boldsymbol{y}$,$\Delta\boldsymbol{s})$ を探索方向とする。
\begin{bmatrix}
A & O & O \\
O & A^T & I \\
\rm{diag} (\boldsymbol{s}_k) & O & \rm{diag} (\boldsymbol{x}_k)
\end{bmatrix}
\begin{bmatrix}
\Delta\boldsymbol{x} \\
\Delta\boldsymbol{y} \\
\Delta\boldsymbol{s}
\end{bmatrix}
=-
\begin{bmatrix}
A\boldsymbol{x}_k-\boldsymbol{b} \\
A^T\boldsymbol{y}_k+\boldsymbol{s}_k-\boldsymbol{c} \\
\rm{diag} (\boldsymbol{x}_k)\boldsymbol{s}_k-\nu_{k+1}\boldsymbol{1}
\end{bmatrix}
制約条件を満たすようにステップ幅 $\alpha_k>0$ を決定し、解を更新する。
(このあたり、Qiitaのインライン数式がバグって数式がうまく書けなかったです。)
4.5 凸2次計画問題とその解法
凸2次計画問題とは、目的関数が凸2次関数で制約がすべて線形な以下のような問題。なお、$Q$ は半正定値対称行列。
\begin{array}
&\min &\frac{1}{2}\boldsymbol{x}^TQ\boldsymbol{x}+\boldsymbol{c}^T\boldsymbol{x} \\
s.t. &A\boldsymbol{x}\geq\boldsymbol{b}
\end{array}
双対問題は以下。
\begin{array}
&\max &-\frac{1}{2}\boldsymbol{x}^TQ\boldsymbol{x}+\boldsymbol{b}^T\boldsymbol{y} \\
s.t. &A^T\boldsymbol{y}-Q\boldsymbol{x}=\boldsymbol{c} \\
&\boldsymbol{y}\geq\boldsymbol{0}
\end{array}
凸2次計画問題は弱双対性・強双対性を持つ。
$\boldsymbol{x}$ および $(\boldsymbol{y},\boldsymbol{x})$ が最適解であるための必要十分条件は以下。
\begin{array}
&A^T\boldsymbol{y}-Q\boldsymbol{x}=\boldsymbol{c} \\
A\boldsymbol{x}-\boldsymbol{b}\geq\boldsymbol{0} \\
\boldsymbol{y}\geq\boldsymbol{0} \\
y_j(A\boldsymbol{x}-\boldsymbol{b})_j=0,~~~~~j=1,\cdots,n
\end{array}
一般の凸2次計画問題の解法としては、内点法が1番有効。線形計画問題と同様にして主双対内点法を設計することができる。
しかし、問題の特殊な構造を活かすことにより、有効制約法と呼ばれる手法を利用してより効率的な方法を構築できる余地がある。有効制約法とは、現在得られている実行可能解において有効な不等式制約のみを取り出して等式制約つき最適化問題を解き、その解がKKT条件を満たしているかチェックする方法。アルゴリズムは以下。
0. $k$ 回目の反復で最適解を得られた場合の有効制約の集合を以下で定義する。
I^k=\lbrace i~|~\boldsymbol{a}_i^T\boldsymbol{x}^k=\boldsymbol{b}_i \rbrace
このとき、相補性条件より $i\notin I^k$ のとき $y_i=0$ だから、以下が成り立つ。有効制約に対応する制約を並べた行列を $\tilde{A}^k$、有効制約に対応する $\boldsymbol{y}$ の成分だけを取り出したベクトルを $\tilde{\boldsymbol{y}}^k$ と書いている。
A^T\boldsymbol{y}^k-Q\boldsymbol{x}^k-\boldsymbol{c}={\tilde{A}^k}^T\tilde{\boldsymbol{y}}_i^k-Q\boldsymbol{x}^k-\boldsymbol{c}=0
さらに有効制約では等式が成り立つ条件も加えると、以下のように書ける。有効制約に対応する $\boldsymbol{b}$ の成分だけを取り出したベクトルを $\tilde{\boldsymbol{b}}$ と書いている。
\begin{bmatrix}
-Q & {\tilde{A}^k}^T \\
{\tilde{A}^k}^T & O
\end{bmatrix}
\begin{bmatrix}
\boldsymbol{x}^k \\
\tilde{\boldsymbol{y}}^k
\end{bmatrix}
=
\begin{bmatrix}
\boldsymbol{c} \\
\tilde{\boldsymbol{b}}^k
\end{bmatrix} \tag{4-4} \label{validConstraintMethod}
- 実行可能解 $\boldsymbol{x}^0$ が得られたとし、$k=0$、$W^0=I^0$ とする。。
- ($\ref{validConstraintMethod}$) を解き、その解を $(\hat{\boldsymbol{x}}^k, \hat{\boldsymbol{y}}^k)$ とする。$\hat{\boldsymbol{x}}^k=\boldsymbol{x}^k$ なら4.へ進む。
- ステップ幅 $\alpha^k$ を適当に決定し、$\boldsymbol{x}^{k+1}=\boldsymbol{x}^k+\alpha(\hat{\boldsymbol{x}}^k-\boldsymbol{x}^k)$ とする。新たに有効になった解があればそれを $W^k$ に加えて $W^{k+1}$ とする。$k=k+1$ として1.へ戻る。
- $\hat{\boldsymbol{y}}^k\geq\boldsymbol{0}$ なら終了し、$\boldsymbol{x}^k$ を最適解として出力。そうでない場合は、以下の更新をして1.に戻る。
\begin{array}
\hat{y}_t^k = \min_{i\in I^k}\hat{y}_i^k \\
W^k=W^k-\lbrace t\rbrace
\end{array}